基于SWIPT 的毫米波大规模MIMO-NOMA系统下安全能效资源优化

赵飞，郝万明，孙钢灿，周一青,3，王飞，王毅

（1.郑州大学河南先进技术研究院，河南 郑州 450003；2.郑州航空工业管理学院智能工程学院，河南 郑州 450046；3.中国科学院计算技术研究所，北京 100190）

1 引言

随着5G 网络逐渐普及，各种智能应用对数据传输速率的要求越来越高。毫米波（30～300 GHz）由于拥有超宽带宽，已作为5G 网络和未来6G 网络实现高速率数据传输的关键技术之一[1]。但是，高频毫米波信号传输衰减较大，基站通常需配备大规模天线，形成高增益方向性波束以提高信号传输距离[2]。对于传统数字编码系统，每根天线需要连接唯一的射频链，由于毫米波射频链硬件功耗较大，大量射频链导致系统功耗很大[3]。为降低毫米波大规模多输入多输出（MIMO,multiple input multiple output）系统的功耗，混合模拟数字预编码技术被提出，它通过减少射频链数目降低系统功耗，从而提高系统能效[4]。另外，非正交多址接入（NOMA,non-orthogonal multiple access）技术通过多用户共享毫米波的波束和频谱，也可以有效地提高系统频谱效率[5]。因此，基于NOMA 的毫米波大规模MIMO 系统可实现未来网络高速率、低功耗、高能效数据传输的目标。

虽然大规模MIMO 可提升系统传输速率，但增加了能源损耗[4]。研究表明5G 网络的能源损耗将是4G 网络的100 倍[6]，因此能源效率将是未来网络一个非常重要的性能指标。为降低系统功耗，提高系统能效，除了混合预编码技术，无线携能通信（SWIPT,simultaneous wireless information and power transfer）技术在近年也受到广泛关注[7-9]。接收端通过功率分配器把接收的射频信号转换为信息和能量[10]，延长了电池的使用时间，为未来拥有海量连接设备的物联网（IoT,Internet of thing）提供巨大的节能潜力[11]。但是对于多用户接入的IoT 系统，用户间的干扰通常不利于信息解码而是有利于能量收集，因此如何有效整合用户间的干扰，平衡信息传输速率和能量收集是多用户接入的IoT 系统面临的一大挑战。

无线通信开放传输的特性使数据传输的安全性受到一定威胁。近年来，联合毫米波、SWIPT 和NOMA 等技术研究如何保证信息安全传输成为热点。文献[12]在用户服务质量（QoS,quality of service）受限情况下研究了SWIPT-NOMA 系统的安全速率传输最大化问题，提出一种粒子群优化算法，有效地提高了系统传输速率。文献[13]考虑用无人机作为移动基站，在毫米波NOMA 系统中存在窃听者监听情况下，提出一种优化无人机基站保护区域的算法，提高了系统的保密速率。文献[14]考虑了一种边缘缓存来辅助毫米波云无线接入网络，研究了安全传输延迟最小化的波束设计问题，提出一种基于半正定松弛的迭代算法，降低了系统的安全传输时延。文献[15]分析了NOMA 系统上行链路的物理层安全性，提出一种优化发射功率和排除窃听者窃听半径的方法，提高了系统安全性能。文献[16]研究了存在窃听者情况下的无线携能系统保密能效最大化问题，提出一种优化算法，该算法将原非凸问题转化为两层优化问题，得到该系统保密能效问题的最优解。文献[17]研究了毫米波NOMA 系统在窃听者存在下的最大安全能效问题，提出了一种连续凸逼近的迭代算法得到原问题的最优解。

文献[12-15]仅研究了如何提高系统安全传输速率，并未考虑系统能效问题。文献[16]仅研究了无线携能系统的保密能效问题，并没有结合当前最新的毫米波、混合预编码、NOMA 等相关技术。文献[17]研究的问题虽然结合了上述技术，但没有引入SWIPT，这对移动设备续航时间和系统能效有着很大的损失。因此本文研究了基于SWIPT 的毫米波大规模MIMO-NOMA 系统如何提高安全能效的问题，其中，所有用户均配备功率分裂器，可以把接收信号分为两部分，一部分用于信息解码，另一部分转化为能量。为有效提高系统安全能效同时降低资源优化复杂度，本文对混合模拟数字预编码和功率分配2 个阶段进行优化设计。其中，对于混合模拟数字预编码的设计，首先根据各用户的信道状态信息获得等效信道增益及其相关性，以此选出簇头并对用户分组；然后根据各个簇头的等效信道进行模拟预编码设计以提高天线阵列增益，再采用破零数字预编码消除簇内等效信道增益最大的用户间干扰；最后形成一个优化发送功率及其功率分配系数的安全能效最大化问题。为求解所形成的优化问题，首先应用Dinkelbach 技术将最初分式目标函数转换为相减形式，然后利用一阶泰勒展开式把原非凸问题转化为凸优化问题，最后提出一种基于采用连续凸逼近（SCA,successive convex approximation）算法和Dinkelbach 两层迭代算法获得最初问题的解。仿真结果表明，与传统数字编码系统相比，本文所提方案可以获得更高的安全能效。

2 系统模型

如图1 所示，考虑存在窃听用户的下行毫米波大规模MIMO-NOMA 系统，该系统包括K个合法用户和一个窃听用户，基站配置NRF个射频链和NTX根天线，合法用户均配有功率分裂器，可以把接收射频信号的一部分转化为能量。

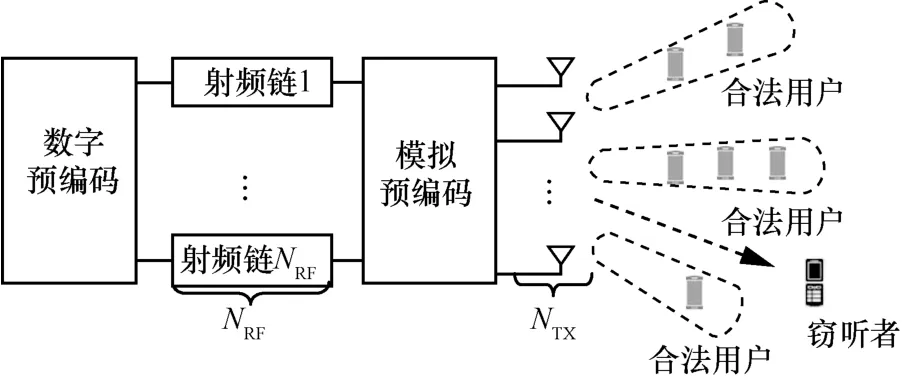
图1 存在窃听用户的下行毫米波大规模MIMO-NOMA 系统

混合模拟数字预编码系统一般分为全连接和子连接2 种结构。全连接结构如图2(a)所示，每条射频链通过NTX个移相器连接所有天线，共需要NTXNRF个移相器。子连接结构如图2(b)所示，每个射频链仅连接一个子天线阵列。假设每个射频链连接根天线且为整数，则基站需要NTX个移相器。与全连接结构相比，子连接结构硬件复杂度较低且节能，但会损耗系统传输速率[18]。

如图1 所示，混合模拟数字预编码系统首先需要对所有合法用户进行分组，并选出各组的簇头，然后根据簇头设计混合预编码，使一个波束通过NOMA 技术来服务该簇内的合法用户。假设每个簇至少包含一个合法用户（即K≥NRF），将K个合法用户分组为L个簇（即NRF=L）。采用文献[18]的方法选出簇头，并根据等效信道互相关性对所有合法用户分为Ml个分组（l∈{1,…,L}），其表示第l个簇中合法用户的集合。

本文利用NOMA 技术和串行干扰消除（SIC,successive interference cancellation）技术来消除波束内较弱信道增益信号对较强信号的干扰。假设每个簇中的合法用户根据信道增益按由强到弱顺序进行排列，第l个簇中第m个合法用户记为合法用户(l,m)，其接收信号为

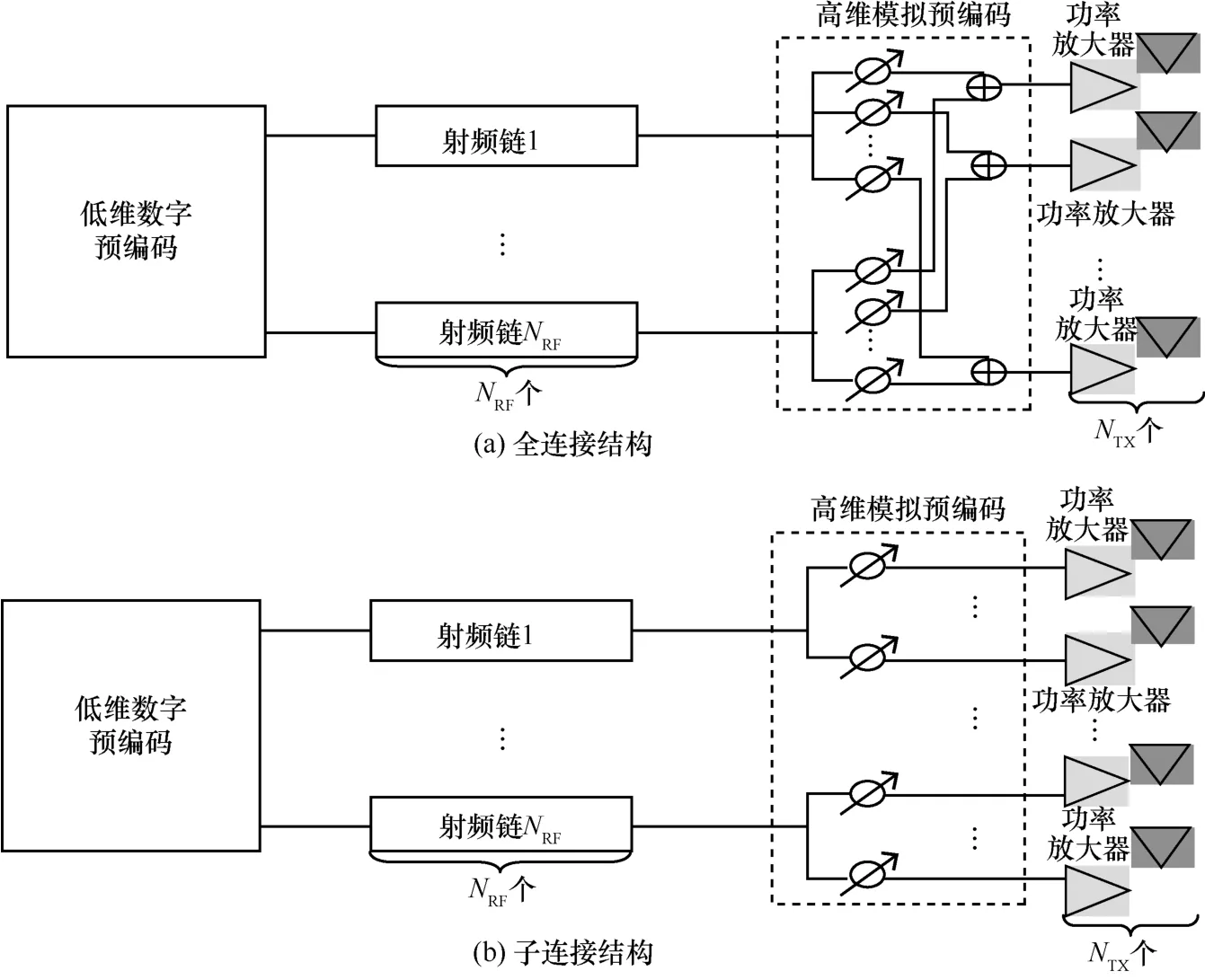
图2 混合模拟数字预编码系统

3 安全能效优化问题及其求解

在完成混合模拟数字预编码的设计后，可以获得用户(l,m)的安全速率，如式(7)所示。

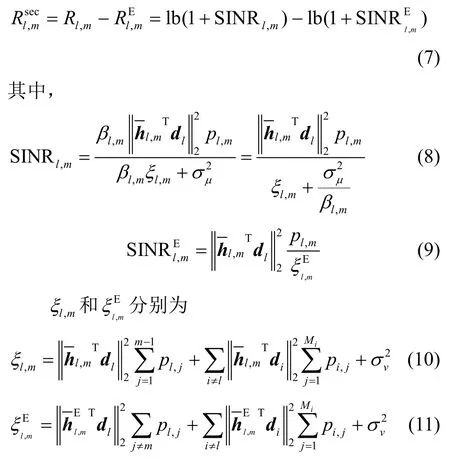
系统功耗包括发射功耗和基站电路功耗，其中，基站电路功耗包括射频链、移相器和基带信号处理的电路功耗，分别用PRF、PPS和PB表示，则总电路功耗为PC=NRFPRF+NPSPPS+PB，系统安全能效最大化优化问题为

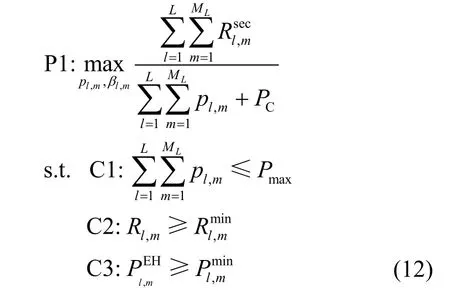
其中，C1 表示基站发射功率限制，C2 表示合法用户(l,m)的数据速率QoS 约束，C3 表示合法用户(l,m)的能量采集QoS 约束。目标函数P1 和约束条件C2和C3 的非凸性导致P1 为一个非凸的优化问题。根据Dinkelbach 算法[19]，将式(12)中的目标函数转换成相减的形式，如式(13)所示。

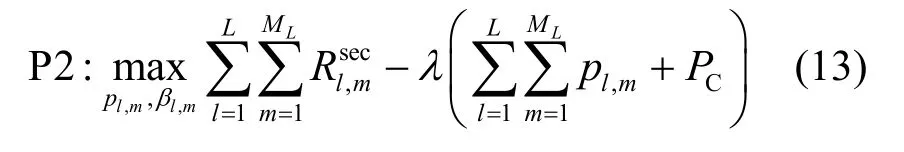
其中，λ是一个非负常数。假设λopt是式(12)所示优化问题的最优解，由Dinkelbach 算法可知[19]，λopt一定满足式(14)所示条件。

将式(19)和式(20)代入式(16)，则目标函数P3转化为凸函数。但问题P3 中的约束条件C2 和C3和新增约束条件C4 均为非凸，首先将C2 转化为式(21)所示的凸的形式。

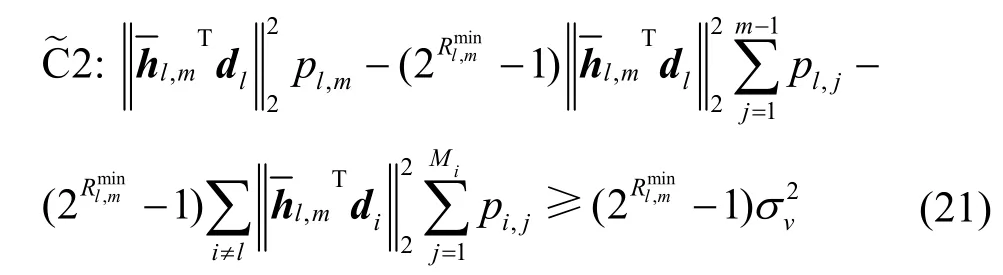
约束条件C3 再引入一个新变量{γl,m}，并且满足式(22)所示约束条件。

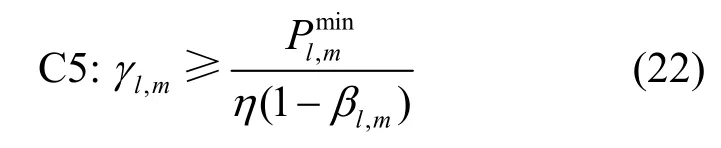
约束条件C3 可重新表示为

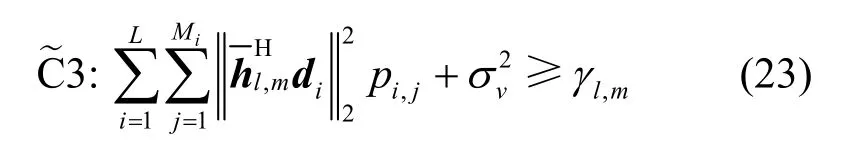
对于新增约束条件C4 和C5 多变量耦合的约束条件，根据舒尔补充引理[21]，将它们转换为矩阵形式，如式(24)和式(25)所示。

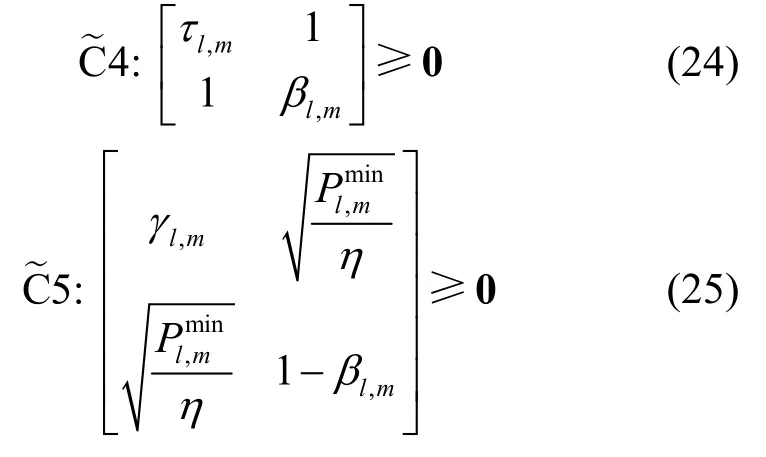
综上所述，目标函数P3 可以转换成式(26)所示形式。

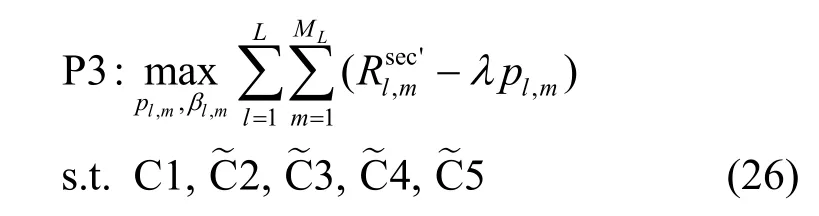
此时，式(26)为一个凸优化问题，可以用凸优化工具箱直接求解[22]。之后采用本文所提出的基于SCA 和Dinkelbach 两层迭代算法得到初始问题P1的最优解，具体算法算法1 所示。

算法1基于SCA 和Dinkelbach 的迭代算法

4 仿真结果与分析

本节通过实验仿真对本文方案得到的安全速率和安全能效进行分析。对基站天线数目NTX=96、射频链数目NRF={4,8}两组进行对比，合法用户数K=10，路径数NP=3，移相器的相位比特数B=4。假设每条射频链的功率PRF=300 mW，移相器功率PPS=40 mW，基带功率PB=200 mW[17]。对于全连接结构和子连接结构所需的移相器个数分别为NPSF=NTXNRF和NPSS=NTX。

本文方案的收敛性能分析如图3 所示。从图3 可以发现，本文方案在内层迭代10 次后频谱效率得到收敛，外层迭代不到20 次收敛曲线便趋于稳定。

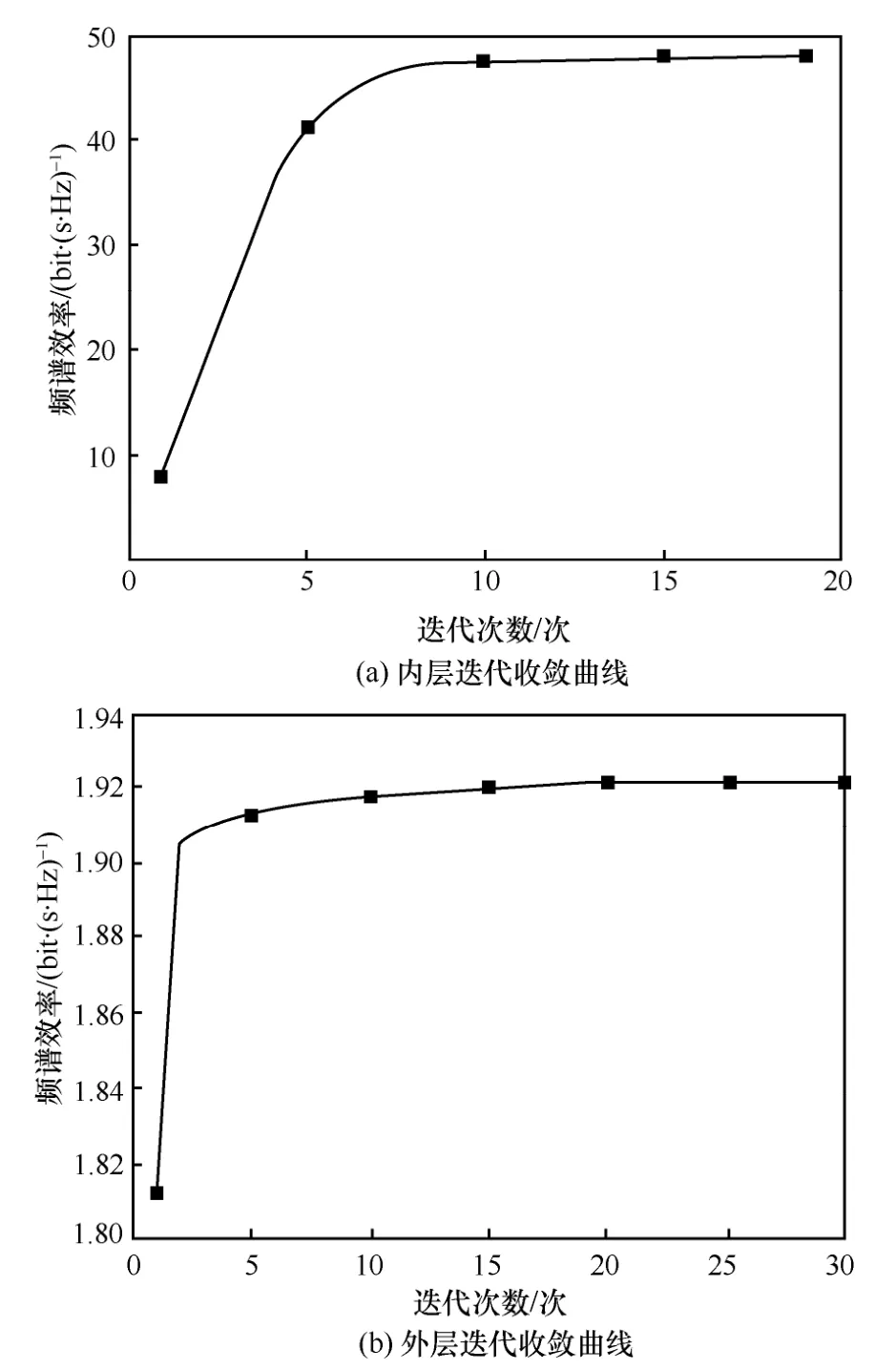
图3 本文方案的收敛性能分析

不同天线结构和不同射频链数目情况下最大安全频谱效率随总发射功率限制Pmax的变化如图4所示。从图4 可以看出，所有结构的安全频谱效率均随Pmax的增大而增大，其中，全数字迫零预编码下的安全速率最高，这是由于每条射频链连接一根天线，可以任意调节信号的幅度和相位，从而获得最大的复用增益。由图4 还可以看出，相同射频链路条件下，全连接结构的安全频谱效率大于子连接结构的安全频谱效率，这是因为全连接结构的每一条射频链连接所有天线实现了全阵列增益，而子连接结构只连接到一个子天线阵列。此外，通过不同射频链数目的比较可以发现，增加射频链数量可以显著提高系统安全频谱效率。

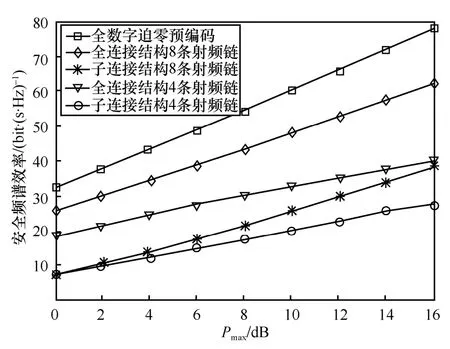
图4 系统安全频谱效率随Pmax 的变化情况

系统安全能效的仿真结果如图5 所示，表示不同天线结构和不同射频链数目情况下最大安全能效随着总发射功率限制Pmax变化的情况。从图5 可以看出，在所有天线结构下，当总发射功率限制Pmax较小时，安全能效均随着Pmax的增大而增大。当Pmax≥8 dB 时，安全能效的曲线趋于水平。这是由于当Pmax较小时，安全能效的增加主要取决于安全速率的增加；而当Pmax达到一定阈值时，安全速率的增加已无法补偿发射功率的消耗，使发射总功率保持不变，安全能效趋于定值。与图4 相反，全数字迫零预编码下的安全能效最低，这是由于庞大射频链极大增加了系统功耗。另外，对于全连接或者子连接结构而言，其安全能效均随着射频链数目的增加而降低，因为更多的射频链虽然可以提高安全速率，但其电路功耗较大从而降低了安全能效。此外，因为子连接结构比全连接结构有更少移相器的能量消耗，所以子连接结构具有更高的安全能效。

系统达到最大安全能效时合法用户发射总功率如图6 所示。从图6 可以看到，总功率Pmax＜4 dB时，所有结构的发射总功率均达到了限制条件Pmax；当Pmax＞10 dB 时，发射总功率均为一个定值，这与图5 相符合。发射总功率在达到定值后，相同射频链数目情况下，子连接结构能耗小于全连接；相同连接结构情况下，4 条射频链能耗小于 8 条射频链能耗；全数字迫零预编码能耗最大。

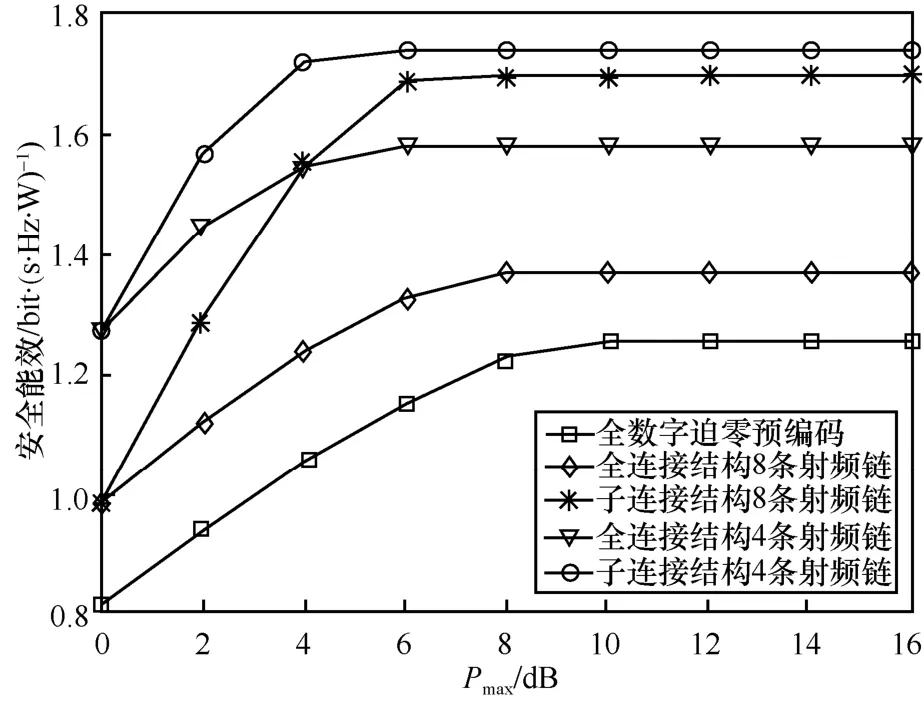
图5 系统安全能效的仿真结果

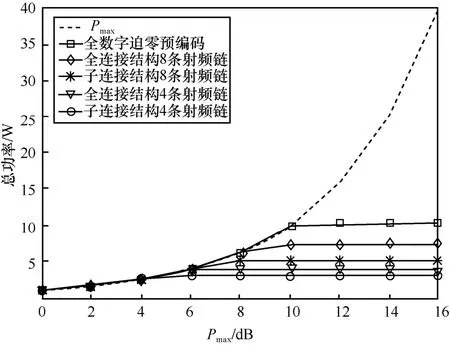
图6 最大安全能效时合法用户发射总功率

5 结束语

本文提出将SWIPT 与基于混合预编码的毫米波大规模MIMO-NOMA 系统相结合，分析该系统存在窃听者时的安全能效问题。混合模拟数字预编码方面考虑了频谱效率较高的全连接结构和能源效率较高的子连接结构，在此基础上结合SWIPT形成一个安全能效最大化的优化问题，同时考虑合法用户的总功率限制、用户速率QoS 和采集能量QoS 的约束。针对该非凸问题，利用一阶泰勒展开式将目标函数转换为凸函数；对于多变量耦合的约束条件通过舒尔补充引理转换成凸的矩阵形式，并提出一种迭代算法求得原始问题的最优解。仿真结果表明，与传统的全数字迫零预编码系统相比，本文提出的预编码安全能效更好，并且对比2 种不同结构的预编码方式的安全速率和安全能效发现，全连接结构比子连接结构的安全速率更高，但子连接结构具有更高的安全能效。