基于Nonce 重用的ACORN v3 状态恢复攻击

张国双，陈晓，林东岱，刘凤梅

（1.中国科学院信息工程研究所，北京 100093；2.中国科学院大学网络空间安全学院，北京 100049；3.信息保障技术重点实验室，北京 100072）

1 引言

加密和认证是密码学的2 个基本属性。在现代网络保密通信中，基于密码构建信息系统对消息进行加密和认证处理，是实现数据机密性和认证性保护的有效途径，然而由于使用不当或恶意敌手后门植入等，可能会造成Nonce 重复使用、未按规则返回明文等情况发生，从而为潜在敌手攻击和分析密码算法提供便利。Nonce 重用的状态与密钥恢复攻击一般模型如图1 所示，攻击者通过植入后门，造成发送方使用相同的Nonce 对不同消息进行加密处理，从而获得不同结构的明文所对应的不同密文。利用这些密文，可对密钥或状态进行恢复分析，一旦成功地恢复出密钥或状态，就可以对保密通信进行实时解密监听或篡改伪造。

图1 Nonce 重用的状态与密钥恢复攻击一般模型

为进一步提升认证加密算法的安全强度，增强人们对认证加密算法的认识和信心，2013 年，国际密码协会（IACR,International Association for Cryptologic Research）面向全球发起了征集认证加密算法的CAESAR（competition for authenticated encryption:security,applicability,and robustness），旨在遴选安全高效的认证加密算法。CAESAR 自2013年开始至2019 年结束持续6 年时间，最终有6 个算法胜出并作为认证加密算法的代表，ACORN v3算法便是其中之一。ACORN 算法由Wu[1]提出，是一个面向比特的轻量认证加密算法，并以其新颖的设计和轻量化高效实现引起了国内外密码学界的广泛关注和研究兴趣。

ACORN 算法自发布以来历经了3 个版本[1-3]，目前的最新版本是ACORN v3。针对ACORN 算法安全性的研究很多[4-19]。其中，关于ACORN 算法的状态或密钥恢复攻击，Liu 等[4]根据ACORN v1的滑动特性，利用差分代数技术给出了Nonce 重用两次时ACORN v1 的状态恢复攻击；Chaigneau 等[5]研究并给出了Nonce多次重用时ACORN v1的密钥恢复攻击；Wang 等[6]研究和评估了Nonce 重用情况下ACORN v2 的状态恢复攻击和复杂度；针对ACORN v2 和v3，Zhang 等[7]进一步研究并给出了Nonce 重用三次情况下的状态恢复攻击。

然而，在实际应用中，Nonce 重用本身是小概率事件，出现Nonce 多次重用的概率就更小，同时，密码系统可能会采用一定的手段来减少Nonce 重用情况的发生。因此，攻击所需要的Nonce 重用次数越多，则实际实施的难度越高，因此Nonce 重用次数的多少是此类攻击是否容易实施的关键指标。

针对以上问题，本文给出了一种仅需Nonce 重用两次的ACORN v3 状态恢复攻击，该攻击通过对中间变量的猜测以期构造尽可能多关于内部状态的线性方程。结果显示，即使Nonce 仅重用两次，对于ACORN v3 同样存在低于穷搜索复杂度的状态恢复攻击，攻击所需的计算复杂度为122.52c，其中，c是求解293 bit 变元线性方程组的复杂度，数据复杂度和存储复杂度可忽略不计。此外，基于本文方法对Nonce 多次重用时的安全性进行分析发现，由于ACORN v3 采用了较之前版本复杂的滤波函数，从而有效避免了通过增加Nonce 重用次数来显著降低状态恢复攻击复杂度的潜在问题。研究结果也进一步印证了ACORN 算法安全性声明中强调的Nonce 不能被重用的要求。表1 给出了ACORN算法状态恢复攻击的结果对比。

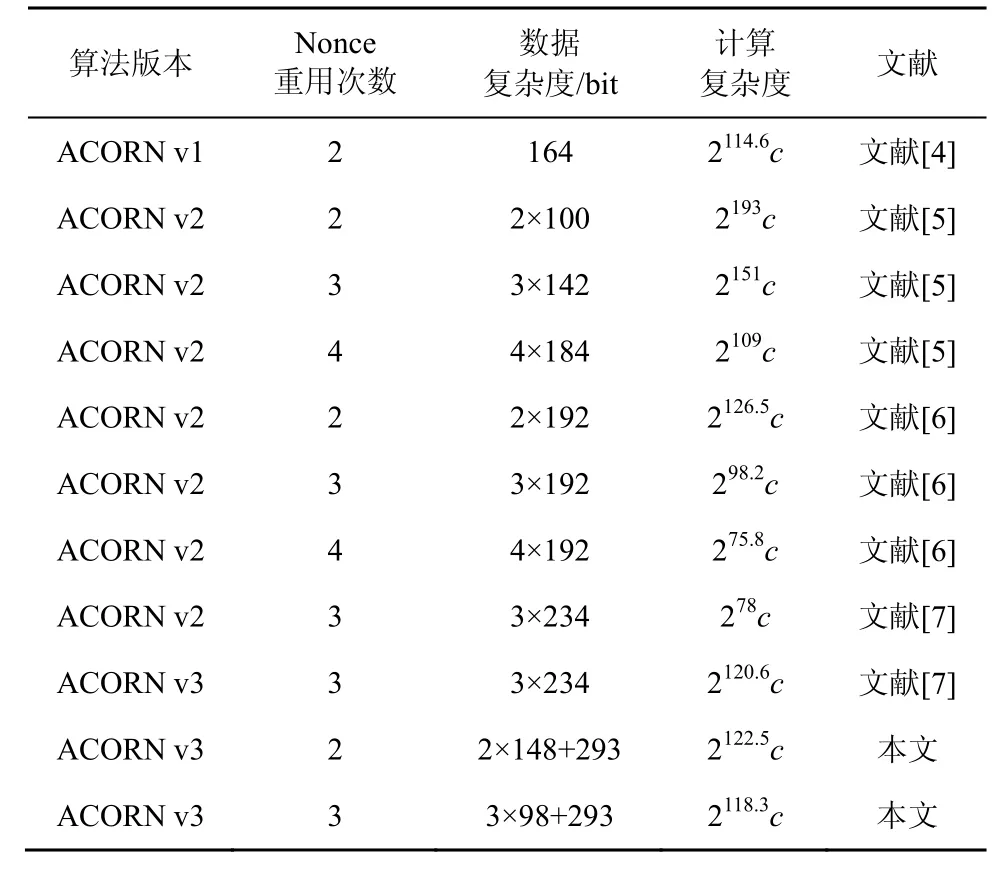
表1 ACORN 算法状态恢复攻击的结果对比

2 符号说明与ACORN 算法简介

2.1 符号说明

本文使用的符号解释如表2 所示。本文约定所有计数从0 开始，并且数据的左侧为最低位，右侧为最高位。

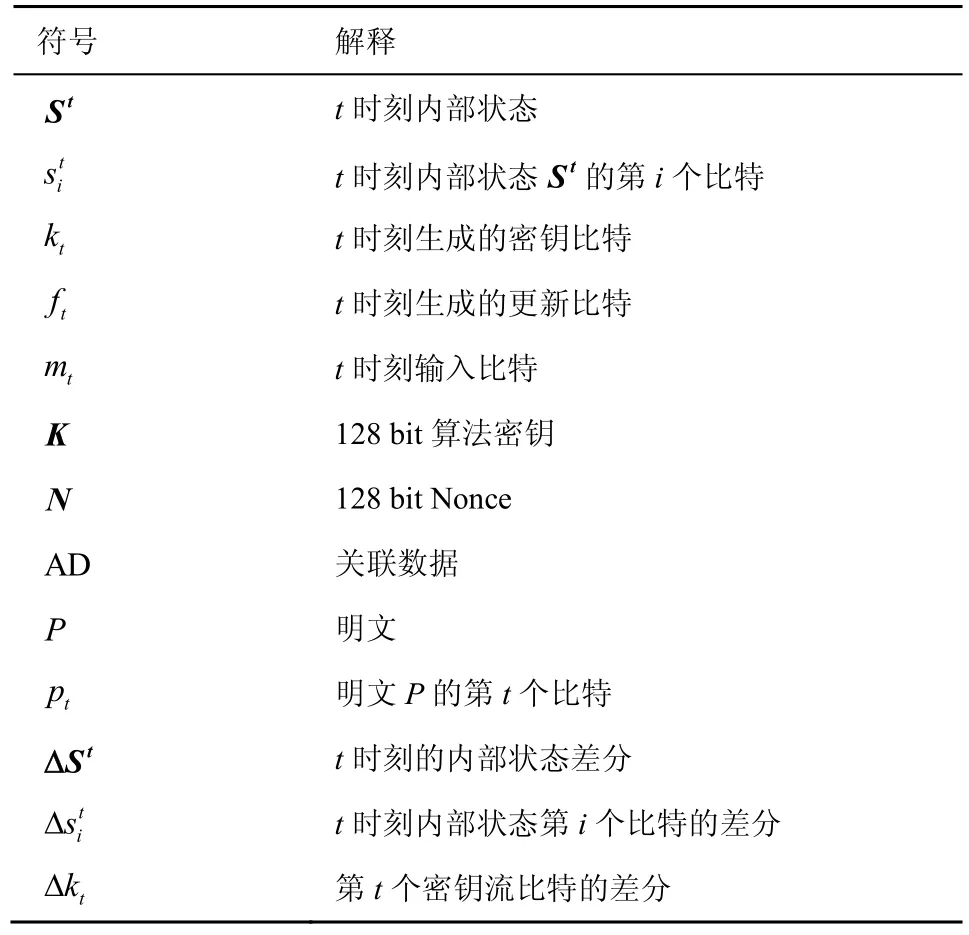
表2 符号解释

2.2 ACORN 算法简介

ACORN 算法利用128 bit 的密钥和128 bit Nonce 可以完成对长度不超过642 的明文和关联数据的保护，并产生长度不超过128 bit 的认证标签。ACORN 采用特定设计的序列密码结构，由6 个不同的线性移位寄存器和一个4 bit 的缓存器构成293 bit 状态移位寄存器，整体采用二次的反馈函数，根据额外的输入比特对内部状态进行更新，并使用二次的密钥流生成函数，每一拍生成1 bit 的密钥，其认证加密过程包含以下4 个环节。

1) 初始化环节。加载密钥和Nonce 并生成初始状态。

2) 关联数据处理环节。处理关联数据并进行内部状态更新。

3) 加密环节。对明文加密并进行内部状态更新。

4) 认证码生成环节。用于生成认证标签。

与ACORN v1 相比，ACORN v2 对初始化过程进行了修改，并调整了4 个环节迭代的拍数；相对于ACORN v2，ACORN v3 对密钥流生成函数和反馈函数进行了调整。以下简要介绍与本文分析有关的ACORN v3 的主要变换环节。ACORN v3 算法的原理如图2 所示。

图2 中，kt、ft和mt分别是密钥比特、状态更新比特和输入比特；at和bt是2 个控制比特，影响ft的计算；maj(⋅)和ch(⋅)是定义在GF(2)上的2 个三元布尔函数；密钥流生成函数和更新比特生成函数分别用于生成密钥比特和状态更新比特。令t时刻ACORN v3 的内部状态，则有密钥流生成函数k t=G(St)。

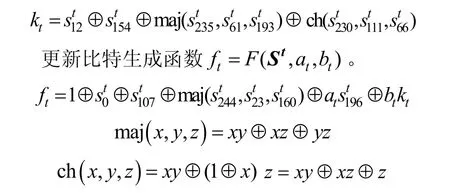
ACORN v3 的状态更新变换包括LFSR（linear feedback shift register）状态线性更新、计算并生成密钥流比特、计算并生成非线性反馈比特和293 级移位寄存器状态更新。记状态更新变换为

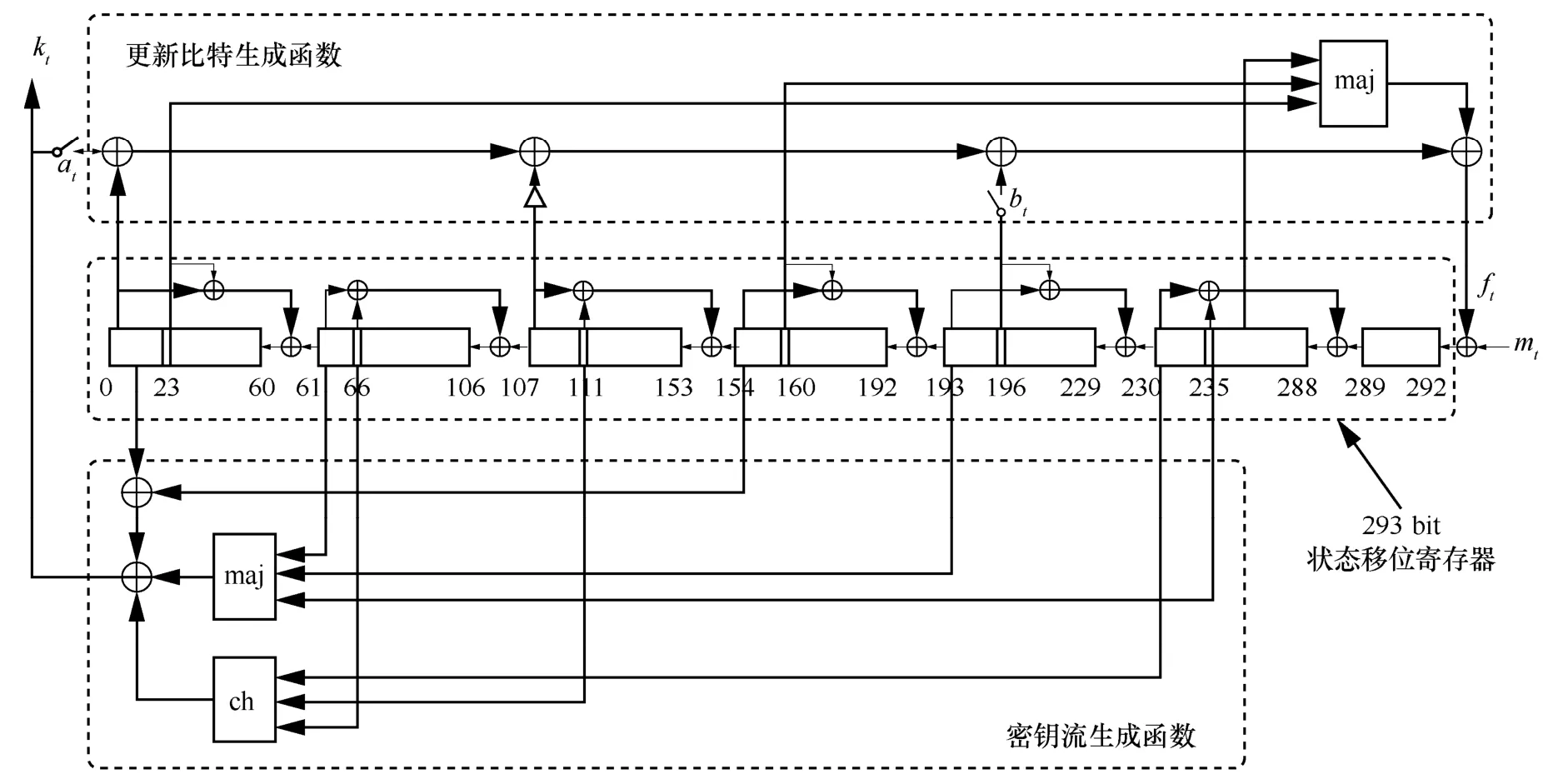
图2 ACORN v3 算法的原理

则状态更新变换的具体过程如下。

Step1LFSR 状态线性更新。

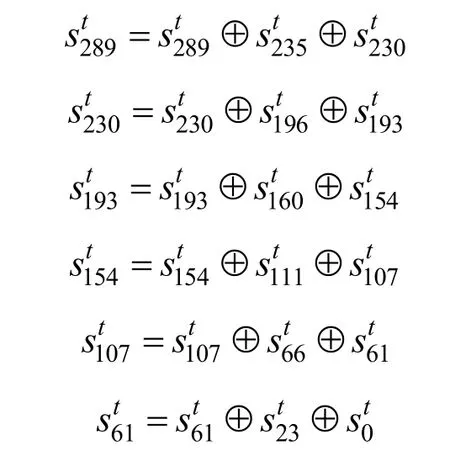
Step2计算并生成密钥流比特。

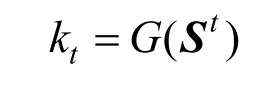
Step3计算并生成状态更新比特。

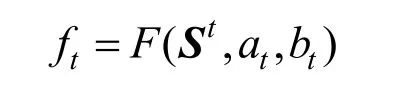
Step4293 级移位寄存器状态更新。

ACORN v3 的4 个环节（初始化环节、关联数据处理环节、加密环节和认证码生成环节）中控制比特at、bt取值与输入比特mt的对应关系如表3所示。

K和N分别表示128 bit 的密钥和Nonce，K′表示将K的最高比特位取反其余比特位保持不变，AD 和P分别表示待处理的关联数据和明文数据。密文比特ct=pt⊕kt，认证码T由最后lbit 的密钥流给定。

3 ACORN v3 状态差分特性分析

本节挖掘了maj(⋅)和ch(⋅)的4 条性质，并结合文献[5]中提出的一条性质，共同推出了ACORN v3加密过程的状态差分传播规律。

3.1 ACORN 算法函数性质研究

maj(⋅)和ch(⋅)是ACORN 算法中用到的2 个最基本的非线性函数。2015 年，Chaigneau 等[5]在对ACORN v1 的状态恢复攻击中发现，maj(⋅)函数具有性质1。

性质1～性质5 的意义有以下几个方面。

1) 给出了函数maj(⋅)和ch(⋅)特定形式输入差分所对应的输出差分的形式。例如，对于函数maj(x,y,z)，若输入差分Δx=1，Δy=Δz=0，由性质1 可知，对应的输出差分为y⊕z。

2) 给出了由输出构建关于输入的线性方程的方法。例如，对于函数ch(x,y,z)，若已知输出a和b，并且Δx=1，Δy=Δz=0，则由性质4 可以建立关于(x,y,z)的2 个线性方程，分别为y⊕z=a⊕b和(a⊕b)x=a⊕z。

表3 控制比特取值与输入比特对应关系

3) 给出了函数maj(⋅)的另外2 种表示形式及其线性化的方法，主要用于第4 部分由猜测确定的方式来构建和提取线性方程。

3.2 ACORN v3 状态差分传播规律

由前面算法介绍可知，在ACORN v3 的加密过程中，每拍生成的密钥比特不进行反馈，状态更新变换根据输入的明文比特对内部状态进行更新。此时在选择明文攻击条件下，攻击者可以通过控制明文输入来影响内部状态，从而得到对其攻击有利的内部状态和密钥流，进而对内部状态或密钥进行攻击。下面，假设攻击者可以控制明文输入比特的差分，对ACORN v3 加密过程的内部状态差分传播情况进行分析。

设初始内部状态差分ΔS0=(0,0,…,0)，明文输入比特差分tmΔ 满足

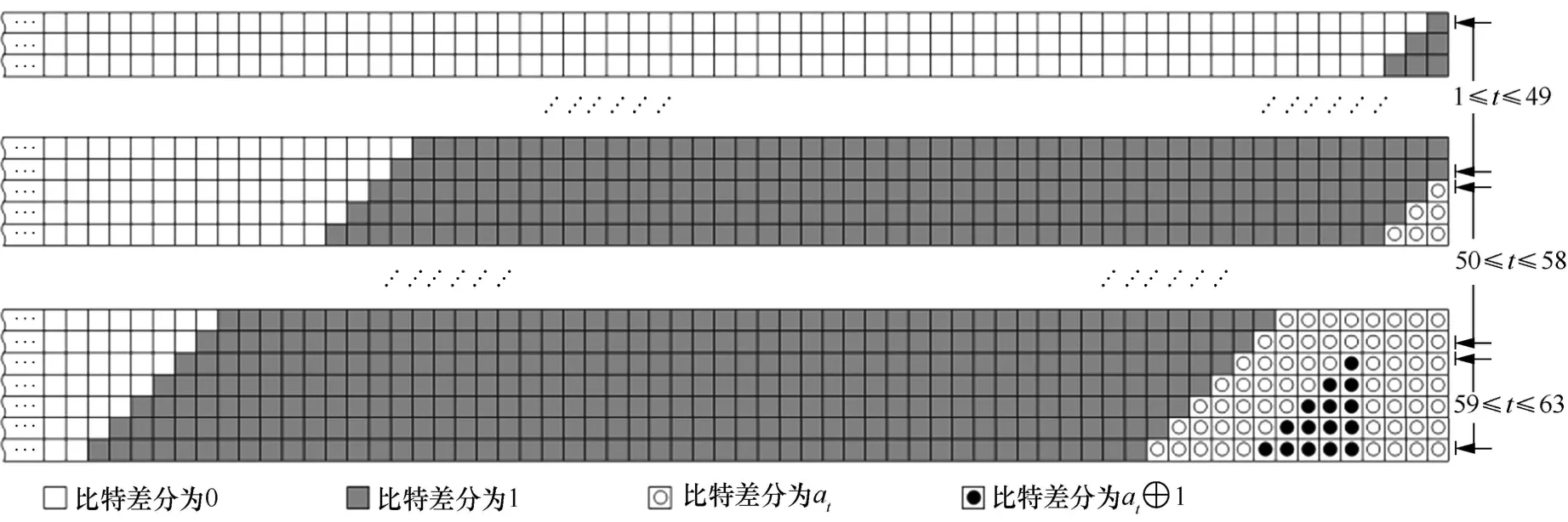
图3 部分内部状态差分传播示意

同理可以得出101≤ t≤148时内部状态差分ΔSt的形式，详细推理过程这里不再给出，具体形式如附录（式(7)～式(14)）所示。以上分析说明，ACORN v3 算法加密过程的内部状态差分具有特定的传播规律。对于Nonce 重用的情况，假设关联数据相同，由于使用了相同的密钥和Nonce，因此加密起始时刻的内部状态相同，若加密的明文差分满足式(1)的形式，则上述状态差分传播规律同样成立，对此有以下结论。

命题1对于ACORN v3 算法，假设用相同的密钥和 Nonce 分别对消息M0=AD||P0和消息M1=AD||P1进行处理，记加密过程起始时刻的内部状态差分为ΔS0，若明文 P0和 P1的前49 bit 差分为1，后99 bit 差分为0，其余位置差分不做要求，则当1≤ t≤148时，内部状态差分ΔSt具有式(2)～式(14)的形式和传播规律。

4 ACORN v3 算法的状态恢复攻击

本节基于上文所述内部状态差分传播规律，利用差分代数技术，给出由密钥流差分通过猜测确定的方式建立关于内部状态线性方程的方法和具体过程，进而对ACORN v3 算法的状态恢复攻击和复杂度进行评估。

4.1 密钥流生成函数特性分析

为了减少硬件开销，ACORN v3 算法采用了基于比特的二次布尔函数作为密钥流生成函数，且形式上比较简单，关于该函数本文给出以下性质。

上述证明中，对于每一种情况的猜测方式可能是不唯一的。例如，4)中也可以通过猜测来构建线性方程，这里仅给出其中的一种，更多的不再列出。性质6 同时给出了通过猜测确定方式，由密钥流及其差分建立关于内部状态线性方程的基本思想和方法，具体如下。若已知输出的密钥流和经线性更新后的内部状态差分，假设内部状态差分的第235、193、230 分位的不全为0，并且第12、61、111、66 分位的差分均为0，由性质6 可知，此时进行1 bit 猜测，可以得到关于内部状态的3 个线性方程。基于此，下面给出Nonce 重用两次的ACORN v3 状态恢复攻击。

4.2 Nonce 重用两次的ACORN v3 状态恢复攻击

4.3 复杂度分析

算法1 需要2(148 +l) bit 的密钥流，其中l≥0，其计算复杂度主要由Step2 和Step3 决定，Step1 和Step5 的计算复杂度可忽略不计，假设Step2 需要进行nbit 猜测，Step3 中求解293 bit 变元线性方程组的复杂度记为c，并假设Step4 中候选值的个数相对于nbit 的猜测是可忽略的，则攻击算法1 的计算复杂度约为2nc。下面对Step2 需要进行猜测的比特个数进行估计。前148 bit 用于Step2 线性方程的构建，并且k0,t的最后lbit 用于Step4 中对候选值进行验证和筛选，本文选择l=293，因此算法1 所需的数据复杂度为2 ×1 48 +293 bit 的选择明文；Step1 和Step5 的计算复杂度可忽略不计，记Step3 中求解293 bit 变元线性方程组的复杂度为c，Step2 平均进行123.25 bit的猜测，可以得到294.75 个关于内部状态的线性方程，假设线性无关的方程的个数是293，则Step3有唯一解，此时Step2 和Step3 的计算复杂度约为2123.25c；如果Step2 中进行122.25 bit 的猜测，则平均可以得到292.75 个线性方程，假设这些方程是线性无关的，则Step2 和Step3 的计算复杂度约为2122.5c；另外，假设对于Step2 中错误的猜测在Step3中以很大概率无解，即Step4 中候选值的个数远小于Step2 的猜测量，则Step4 的计算复杂度相对于2122.5c是可忽略的，综合可得，算法1 的计算复杂度约为 2122.5c，算法所需的存储复杂度可忽略不计。

证毕。

4.4 Nonce 多次重用的安全性分析

对Nonce 重用三次、四次的情况，有以下分析结果。

对于Nonce 重用三次的情况，假设P0、P1和P2用相同的Nonce 进行加密，为了尽可能使得到的方程是线性无关的，令P0、P1、P2满足以下形式。

其中，n是需要猜测的变量αt的个数，此时通过引入49+n个新增变量，可以得到294+5n个线性方程和49 个二次方程，由文献[7]可知，这49 个二次方程能够以20.32 的复杂度进行线性化，对应得到49 个线性方程，此时若要使方程有唯一解，需294+5n+49≥293+49+n，即n≥0，因此需要猜测的变量个数为98，对应的状态恢复攻击的复杂度为 220.3×298c=2118.3c。

对于Nonce 重用四次的情况，根据上述分析，令需要猜测的变量αt的个数为0，需要猜测的变量βt的个数为n，此时通过引入 98 个新变量，可以得147+2n个线性方程和98 个二次方程，98 个二次方程能够以40.62 的复杂度进行线性化，对应得到98 个线性方程，当n≥73时，147 +2n+98 ≥293 +98恒成立，此时选择P0、P1、P2、P3形式如下。

通过对73 个变量βt进行猜测和对98 个二次方程的线性化，恰好可以得到391 个线性方程，对应的状态恢复攻击的复杂度为 240.6×273c=2113.6c。

类似地，可以对Nonce 重用更多次的情况进行分析，状态恢复攻击复杂度估计如表4 所示。

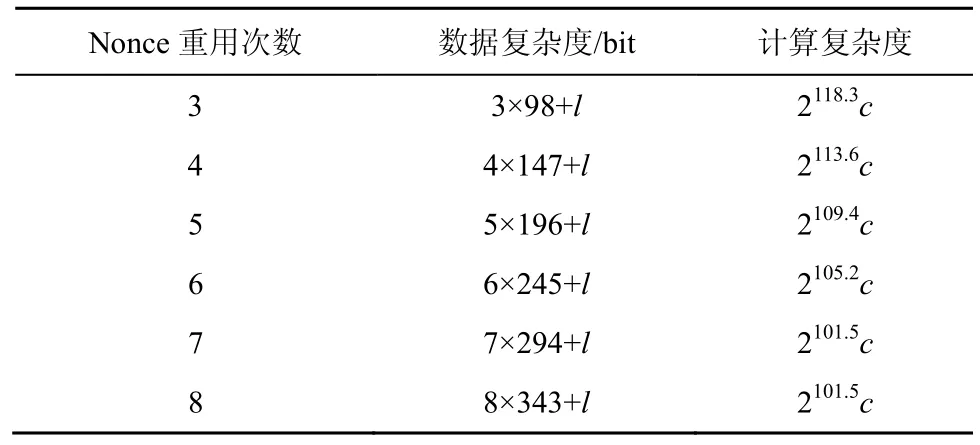
表4 Nonce 多次重用的状态恢复攻击复杂度估计

表4 中可以选择l=293。由表4 的数据和结果可以看出，相对于之前的版本（ACORN v2 和ACORN v1），由于ACORN v3 采用了相对复杂的滤波函数，增加了冗余，使通过增加Nonce 重用次数来大幅降低攻击复杂度的方法很难奏效，从而有效降低了Nonce 多次重用时的安全风险。

4.5 基于已知初始状态的伪造攻击

由于ACORN 算法采用了特定设计的序列密码结构，因此初始状态对算法整体安全性的影响至关重要，对于早期的ACORN v1，由于其初始化过程是可逆的，一旦恢复初始状态，就可以利用初始化过程的逆变换逐步求解和恢复密钥，从而实现对密码算法的完全破解；对于ACORN v2和ACORN v3，由于采用了不可逆的初始化过程，很难由初始状态来恢复和求解密钥，尽管如此，攻击者仍然可以利用所恢复的初始状态实现对任意消息的加密和认证标签的生成，从而进行伪造攻击。

5 结束语

本文分析了ACORN v3在Nonce重用两次情况下的安全性，结果表明，基于差分代数的方法，通过对中间变量进行猜测来对ACORN v3 的密钥流生成函数进行线性化，可以由密钥流及其差分构造足够多的关于内部状态的线性方程，进而通过求解线性方程组实现对ACORN v3 的状态恢复攻击。尽管本文的分析结果远没到实际可行的程度，但进一步完善了ACORN v3算法Nonce重用条件下的安全性分析结果。另外，基于本文方法对Nonce 多次重用情况的安全性进行的分析和评估发现，由于ACORN v3 采用了较之前版本复杂的滤波函数，避免了通过增加Nonce 重用次数来显著降低状态恢复攻击复杂度的潜在问题。最后，关于ACORN 算法的可证明安全性研究是很必要的，可以从差分和线性指标的可控性等方面对算法的可证明安全性进行研究，这将是下一步研究工作的重点。

附录 101≤t≤1 48时内部状态差分ΔS t形式