环状空间热网供回水压线不对称性研究

2020-09-08李铮伟

煤气与热力 2020年8期

杨光，王海, 李铮伟

(同济大学机械与能源工程学院，上海200092)

1 概述

根据清华大学建筑节能研究中心与国际能源署(IEA)联合发布的2017年《中国区域清洁供暖发展研究报告》，2015年中国的集中供热系统规模已跃居世界首位。《中国清洁供热产业发展报告(2019)》显示，截至2017年底，北方地区供热总面积达232×108m2，已有41%实现了清洁供暖。中国政府十部委联合印发的《北方地区冬季清洁取暖规划2017—2021》提出，到2021年底，综合清洁供暖率需从2016年的34%提升到70%的重大任务。

集中供热系统具有显著的动态性和复杂性，需要借助信息技术构建智慧供热系统以提升集中供热全过程的动态协同、协调能力。Lund等人[1-2]提出供热系统将发展为第4代供热系统(智慧供热系统)，并且量化了智慧供热系统在未来可持续能源系统中的成本和效益：成本包括供热系统的升级和热网的运行，效益包括降低热网损耗，更好地利用低温热源和提高生产效率。Rehman等人[3]对智慧供热系统的重要构成部分及技术领先的国家进行了综述，包括斯堪的纳维亚半岛的可持续热源、东欧细致的热网、中国创新的分布式拓扑热网以及中欧正在深入研究的热能储能技术。

智慧供热要求借助信息系统承载知识和经验，辅助和提升人的决策水平，实现供热系统优化调控、故障诊断等智能化功能。在优化调控方面，Wang等人[4]提出了一种基于云计算、远程控制技术的分布式循环泵精确变频方法，该方法可精确调节水泵频率达到0.001 Hz，节约20%以上的耗电量。Wang等人[5]还对多热源管网提出了一种粗调节与细调节相结合的运行方法，可在满足用户供热需求的前提下实现热源供热费用与循环泵耗电费总和最低。在故障诊断方面，国内外针对热网阻力系数的辨识[6]、管段堵塞故障的诊断[7]以及管段泄漏的诊断分析[8]等开展了研究。

精细的供热系统仿真模型对实现优化调控、故障诊断等功能有着重要作用，是实现智慧供热必不可少的基础和工具。传统热网模型在水力计算时普遍采用供回水管网完全对称假设，基于平面热网的方法仅对供回水管道二者之一单独计算[9]。在实际供热管网中，由于管子粗糙度差异、管段堵塞、泄漏等原因，供水管道与回水管道并非完全水力对称。针对供回水管网中某管段发生故障进行检修时的场景，王晓霞等人[10]开创了热网空间拓扑结构研究的先例。周鹏[11]探讨了采取空间管网方法建模的必要性。面对空间热网的拓扑解析问题，周海舰等人[12]提出了一种新的面向对象方法，这种方法可普遍适用于供回水不对称的空间管网。利用该方法，王海等人[13-14]对多热源环状热网进行水力计算并取得了良好的效果，并对管网热力模型进行改进，提出新的数值解法[15-16]。王海等人[17]还基于该方法，讨论了管网的水力不对称性，但是该研究中热源流量和热用户均简化成节点流量进行处理，热网依旧可以拆分成供水、回水两个系统，分别按照平面管网进行计算，并未突出该方法针对空间热网仿真的优势。

本文在文献[17]的基础上，增加热源循环泵特性，分析供回水管粗糙度(本文指绝对粗糙度)、管段堵塞、泄漏对管网供回水压线对称性的影响。

2 水力模型

采用面向对象水力计算方法对空间热网的拓扑结构进行解析时，对供热系统中的每个元件都进行“对象化”建模。对管道、热源、用户等分别建立各自的“对象”，然后根据“对象”之间的拓扑关系，建立符合物理守恒定律的参数传递，进而得到水力模型。

① 管道

管道的水力模型可根据其连续性方程、动量方程联合建立：

式中ρ——水的密度，kg/m3

t——时间，s

u——水的流速，m/s

x——管段轴向长度，m

p——压力(绝对压力)，Pa

f——摩擦阻力系数

d——管道内直径，m

g——重力加速度，m/s2，本文取9.8 m/s2

θ——管段水平倾角，rad

摩擦阻力系数f采用Colebrook & White(C-W)方程计算，表达式为[18]：

式中ε——管子粗糙度，m

Re——水的雷诺数

② 热源

热源类型广泛，除热电厂、锅炉房外，还有多种可再生能源和余热资源等。但从水力建模的角度，可以简化热源的水力性质。对含有定压点的热源，回水压力可直接设置为定压点压力，即：

pr=pset

式中pr——回水压力，Pa

pset——定压点压力，Pa

热源的供回压差由循环泵提供，当确定循环泵流量和运行频率时，循环泵压头可通过水泵特性曲线确定。由此，热源的水力模型为[19]：

ρgHp=ps-pr+Δp

式中Hp——水泵扬程，m

ps——供水压力，Pa

Δp——热源内部阻力，Pa

k0、k1、k2——水泵回归系数

qp——循环泵流量，m3/s

n——水泵实际转速，min-1

n0——水泵额定转速，min-1

③ 用户

为简化热网水力模型，用户可设定为一个阻力节点，水头损失Δhm根据运行数据回归为多项式[19]：

式中 Δhm——用户水头损失，m

r0、r1、r2——回归系数

qm——用户流量，m3/s

当建立热网各对象的水力模型后，对热网进行水力计算，可得到全网各节点和管段的水力参数[12]。

3 算例分析

3.1 概况

选取有2个热源的环状空间热网，拓扑结构见图1[17]。

对于图1，供水主管网布置在顶面，由管段1～22组成。回水主管网布置在底面，由管段47～68组成。含有热源和用户的支网由竖直管段23～46组成。两组循环泵与热源分别由管段69、70连接。箭头表示预设的水流方向，若水流方向与预设方向相同，则流量为正；反之，流量为负。

图1 供热系统的拓扑结构

输入条件：设定在热源S1处采用补水泵定压，定压点压力为500 kPa。热源S1、S2内部阻力均为50 kPa。热用户的设计流量均为180 m3/h，管子粗糙度的初始值设定为0.5 mm，各管段的内直径、长度见表1。循环泵P1、P2的流量-扬程曲线分别见图2、3。在输入条件下，根据模拟结果可知热源S1的设计流量为720 m3/h，热源S2的设计流量为1 080 m3/h，循环泵P1的扬程为15 m，循环泵P2的扬程为21.3 m。

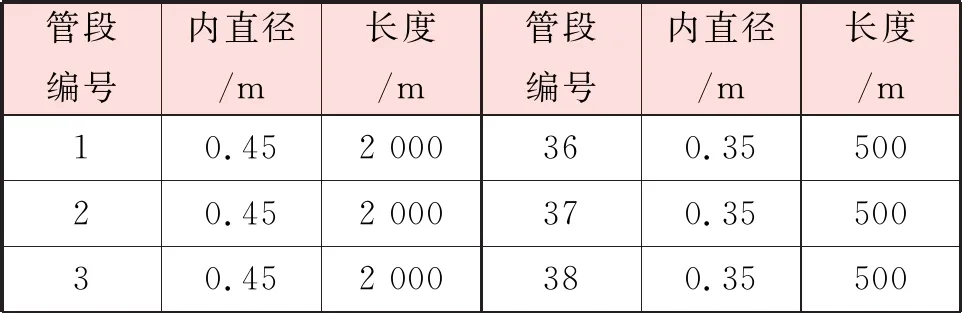
表1 各管段的内直径、长度

续表1

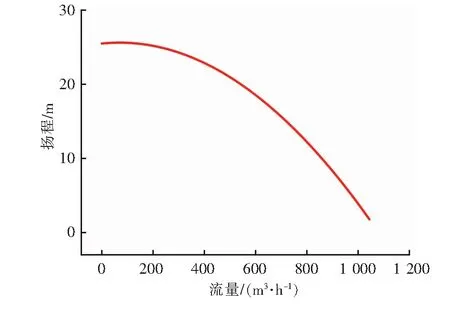
图2 循环泵P1的流量-扬程曲线

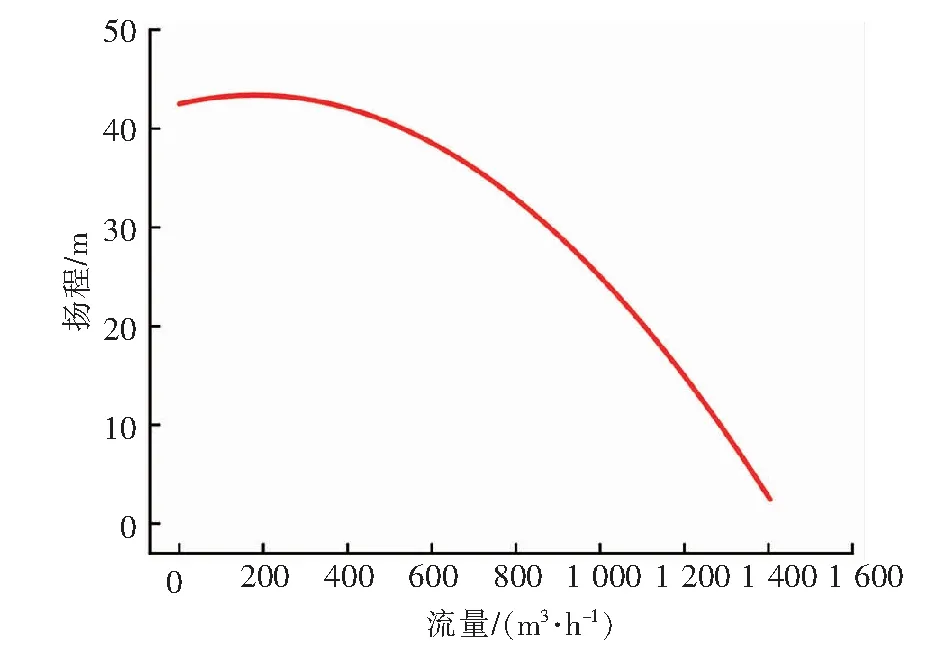
图3 循环泵P2的流量-扬程曲线

3.2 供回水压线对称性影响因素

① 回水主管粗糙度

供水主管、支管粗糙度保持0.5 mm，回水主管粗糙度分别设定为0.1、0.5、1.0 mm。选取以下供回水主管的供回水压线进行分析：供水主管：节点S1-3001-3002-3003-3023-3022-3024-4001-3006-S2；回水主管：节点P1-3011-3012-3013-3027-3031-3032-4004-3016-P2。

根据水力模型，计算得到的不同回水主管粗糙度下的供回水压线见图4，图中横坐标标值括号中数值为回水主管节点编号。由图4可知，与供回水主管粗糙度一致时相比，当供回水管粗糙度不同时，供回水压线出现不对称。

图4 不同回水主管粗糙度下的供回水压线

为了更加直观反映回水主管粗糙度的变化对供回水压线不对称性的影响，笔者计算出各节点的供回水压力平均值(算术平均值)，见图5。由图5可知，当回水主管粗糙度偏离0.5 mm，供回水压线即出现不对称现象。回水主管粗糙度越小，不对称情况越明显。

图5 各节点的供回水压力平均值

② 管段堵塞

仍选取上述供回水主管进行分析，堵塞管段分别选取供水主管的管段17、14以及对应的回水主管的管段59、66。供回水主管、支管粗糙度均为0.5 mm。管段17、59分别堵塞时的供回水压线见图6，管段14、66分别堵塞时的供回水压线见图7。由图6、7可知，供回水主管堵塞均导致供回水压线不对称。与回水主管堵塞相比，供水主管堵塞是导致供回水压线不对称的主要原因。

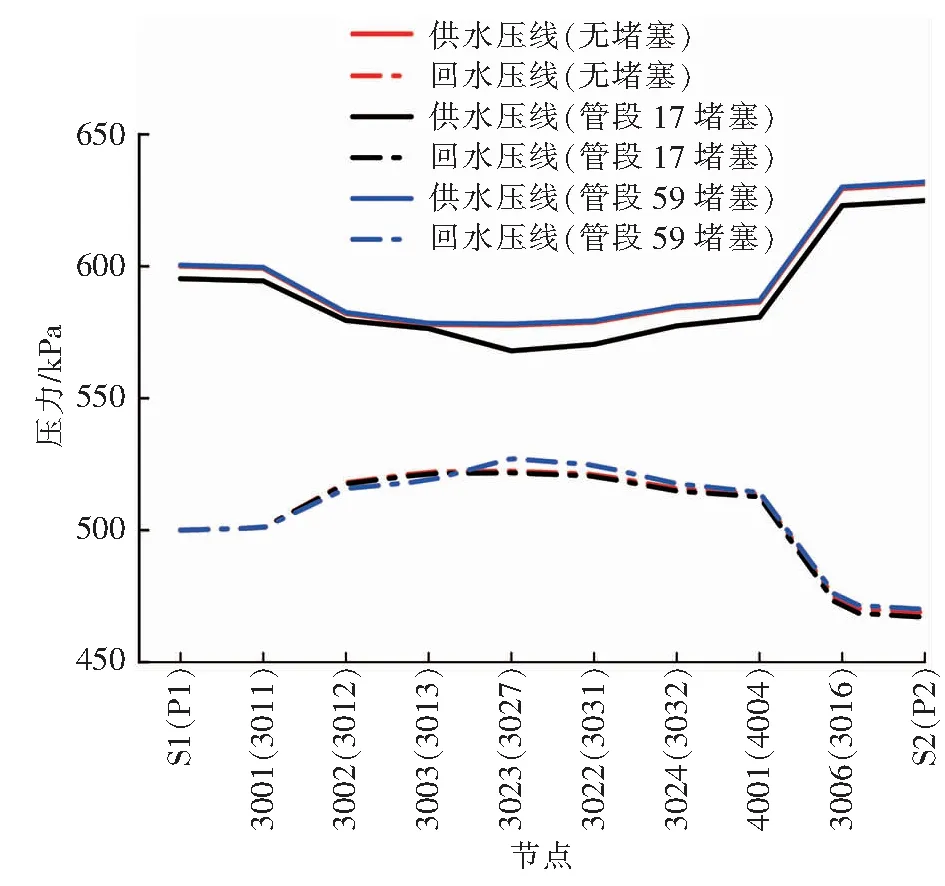
图6 管段17、59分别堵塞时的供回水压线

图7 管段14、66分别堵塞时的供回水压线

③ 管段泄漏

仍选取上述供回水主管进行分析，泄漏管段分别选取供水主管的管段1、12以及对应的回水主管的管段47、58，泄漏位置位于泄漏管段中间。供回水主管、支管粗糙度均为0.5 mm。

泄漏量为总流量的1%，管段1、12分别泄漏时的供回水压线见图8，管段47、58分别泄漏时的供回水压线见图9。由图8、9可知，与回水主管泄漏相比，供水主管的泄漏是导致供回水压线不对称的主要原因。笔者还对泄漏量为总流量的2%、4%、10%的情况进行了计算，结果显示：泄漏量越大，由供水主管泄漏引起的供回水压线的不对称越明显。