一类时滞SIRS微信信息传播模型稳定性和Hopf分岔
2020-09-07门秀萍张子振
曹 春,门秀萍,张子振
(安徽财经大学管理科学与工程学院,安徽蚌埠233030)
根据中国互联网中心第43次中国互联网络发展状况统计,截至2018年12月,我国手机网民规模达8.17 亿,其中手机即时通信用户达7.80 亿,占手机网民的95.5%[1]。微信及WeChat 月活跃账户总计达10.825亿,微信成为了亚洲用户量最多的即时通讯软件。然而,随着微信平台用户的不断增多以及微信使用过程中产生的信息量的不断增加,公共部门管控非法网络信息和防护网络信息安全变得更加困难[2-3],这给社会和个人带来了不可忽视的安全风险[4]。因此,研究微信信息传播过程的特点对管控微信舆论、维护网络安全具有重要意义。
为了研究微信信息传播规律,一些研究者从传染病病毒模型的角度构建信息传播模型以描述微信信息的传播过程。文献[5]以微信朋友圈为研究对象,构建了一种SEIR信息传播动力学模型,以解释朋友圈信息传播规律。文献[6]结合复杂网络理论和传染病动力学,研究了一类SIR信息传播模型,从用户接受阈值和关系动机方面分析微信信息传播的过程。文献[7]在SIR模型的基础上考虑了微信朋友圈紧密度、免疫以及策略改变机制等因素,提出了微信朋友圈信息传播演化规则,构建了微信朋友圈信息传播演化模型。文献[8]基于复杂网络角度,对微信信息传播过程构建Agent模型,分析了微信信息传播演进的过程。上述文献的传播模型均没有考虑在信息传播过程中微信平台用户数量的变化情况,而用户数量对于信息传播过程有着重要影响。最近,文献[9]研究了一类具有输入人群的SIRS微信信息传播模型:

模型(1)中,S表示微信平台上接收到信息的信息敏感用户,I表示接收信息并传播的信息活跃用户,R表示接收到信息但不传播的信息免疫用户,r表示信息的传播率,μ表示用户接收到信息但不再传播的概率,A表示注册到具有该信息的微信平台的用户数量,δ表示不传播该信息的用户回到具有该信息的微信平台的概率,d表示用户接收但不关注该信息的概率。
本文以文献[9]提出的SIRS信息传播模型为基础,引入微信用户的信息临时免疫期时滞,研究了下列具有时滞的SIRS信息传播模型:

其中τ为信息临时免疫期时滞。
1 局部渐近稳定性
计算模型(2)的平衡点,当Ar>μd时,模型(2)存在唯一的平衡点E(S*,I*,R*),其中S*=μ r,R*=(Ar-μd)rd,I*=(δ+d)R*μ。对模型(2)进行线性化处理,即S(t)、I(t)、R(t)做平移变换,令μ1(t)=S(t)-S*,μ2(t)=I(t)-I*,μ3(t)=R(t)-R*,仍然将μ1(t),μ2(t),μ3(t)记作S(t),I(t),R(t)。
通过计算,可以得到模型(2)在平衡点E(S*,I*,R*)处的线性化部分为
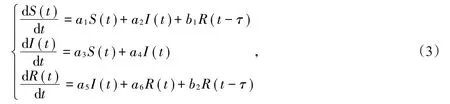
其中,a1=-(rI*+d),a2=-rS*,a3=rI*,a4=rS*-μ,a5=μ,a6=-d,b1=δ,b2=-δ。进而,计算模型(3)的特征方程,得到:

其 中 ,P0=a2a3a6-a1a4a6,P1=a1a4-a2a3+a1a6+a4a6,P2=-(a1+a4+a6),Q0=a2a3b2-a1a4b2-a3a5b1,Q1=a1b2+a4b2,Q2=-b2。
当时滞τ=0 时,方程(4)转化为λ3+P02λ2+P01λ+P00=0,其中,P00=P0+Q0,P01=P1+Q1,P02=P2+Q2。如果劳斯-赫尔维兹稳定性判据成立,即条件(H1):Det1=P02>0,Det2=P02×P01-P00>0 ,Det3=P00×Det2>0,成立,即矩阵的主子式均为正,那么,模型(2)的平衡点E(S*,I*,R*)是局部渐近稳定的。
当时滞τ>0时,令λ=iω(ω>0)为特征方程(4)的根,代入(4)式进行化简计算,可以得到下列等式
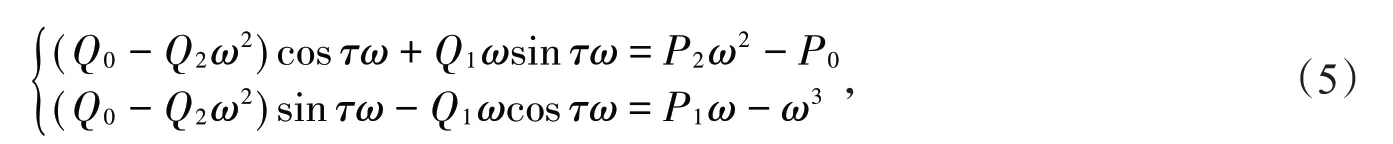
消除(5)式中的三角函数,则

为了得到本文主要结果,给出假设(H2):方程(6)至少存在一个正根。
若假设(H2)成立时,方程(6)存在一个正根ω0使得方程(4)存在一对纯虚根±iω0。对方程(5)进行消除sin函数处理,可以计算得到时滞τ的临界点表达式为

对方程(4)的左右两端分别对τ进行求导,得到
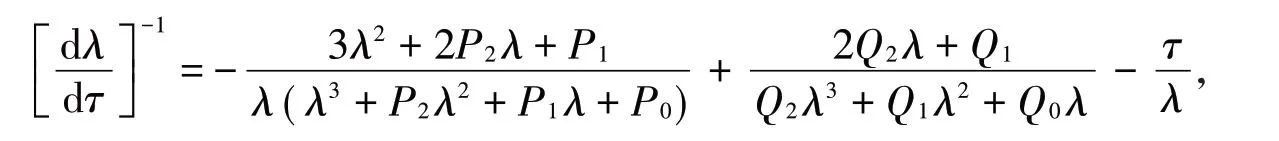
对上面的表达式进行取实数计算,得到实数部分为

显然,如果假设(H3):f′(v*)≠0 成立,那么根据上述分析结果和文献[10]中Hopf分岔理论,可以得到以下结论。
对于模型(2),如果提出的假设(H1)~(H3)均成立,那么当时滞τ∈[0,τ0)时,模型(2)的平衡点E(S*,I*,R*)是局部渐近稳定的;而当时滞τ=τ0时,模型(2)在平衡点E(S*,I*,R*)处失去稳定性并产生Hopf分岔。
2 Hopf分岔方向和分岔周期解
令τ=τ0+μ,μ∈ℝ,那么模型(2)在μ=0 处产生Hopf 分岔。通过定义连续实值函数的空间为C=C([-1,0],ℝ3),Lμ:C→ ℝ3,F:ℝ ×C→ ℝ3,令μ1(t)=S(t)-S*,μ2(t)=I(t)-I*,μ3(t)=R(t)-R*,再对时间延迟进行归一化处理t→(t/τ),可以将模型(2)转换为下列等价模型:μ˙(t)=Lμ μt+F(μ,μt),其中,

由黎兹表示定理可知,存在η(θ,μ),θ∈[-1,0]满足对于φ∈C,可以选择η(θ,μ)=(τ0+μ)(Amaxδ(θ)+Bmaxδ(θ+1)),其中δ(θ)是狄拉克德尔塔函数。
对于φ∈C([-1,0],ℝ3),给出定义

则模型(2)可以转换成下列形式˙(t)=A(μ)μt+R(μ)μt,对于φ∈C1([0,1],(ℝ3)*),则可得A(0)的伴随算子A*
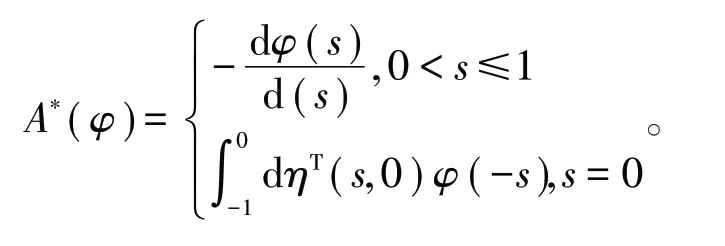
A和A*的双线性内积满足

其中η(θ)=η(θ,0)。
设A(0)的特征值为+iω0τ0时,对应的特征向量为ρ(θ)=(1,ρ2,ρ3)Teiω0τ0θ;A*(0)的特征值为-iω0τ0时,对应的特征向量为计算可以得到

根据文献[10]中的算法,可以得到Hopf 分岔方向和分岔周期解稳定性系数:

计算可得Hopf分岔性质系数

通过上述分析,可以得到下列结论:在模型(2)中,若μ2>0(μ2< 0),Hopf 分岔是超临界的(亚临界的);若β2< 0(β2>0),分岔周期解是稳定的(不稳定的);若T2>0(T2< 0),分岔周期是增大的(减小的)。
3 仿真分析
本文用Matlab软件对建立的时滞微信信息传播模型进行数值模拟分析。对于模型(2)中的参数,取A=2.3,δ=0.4,r=0.9,d=0.15,μ=0.25,可以得到下列信息传播模型:

将参数代入求得的平衡点表达式,得到模型(8)唯一的平衡点为E(0.277 8,33.122 2,15.055 6),将参数代入ω0和时滞τ0的表达式,计算得到ω0=0.217 8,τ0=13.909 5。当τ=8.232 7∈[0,τ0)时,仿真的结果如图1 所示,模型(8)是局部渐近稳定的。当τ=16.352>τ0时,仿真的结果如图2所示,这时模型(8)失去稳定性,产生Hopf分岔。

图1 当时滞τ=8.272 3∈[0,τ0)时,模型(8)渐近稳定
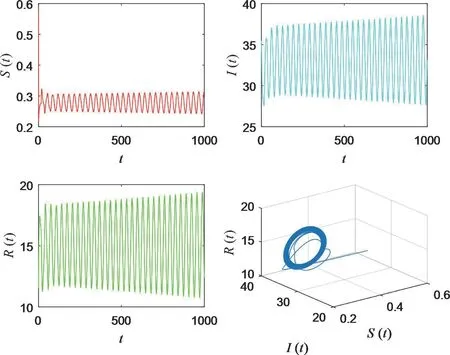
图2 当时滞τ=16.352>τ0时,模型(8)失去稳定并产生Hopf分岔
4 结 论
本文在文献[9]研究工作的基础上,进一步研究了微信平台用户的信息临时免疫期时滞对信息传播的影响,分析了具有时滞的SIRS微信信息传播模型,了解了微信信息的动态传播过程。通过讨论模型特征根的分布,得到了该时滞SIRS模型的局部渐近稳定性和产生Hopf分岔的充分条件。研究和仿真表明,微信信息传播中,用户的信息临时免疫期时滞超过临界值时会使模型失去稳定性,使得模型中的三类用户以周期震荡的形式存在,不利于对微信信息传播过程进行控制。因此,为了有效控制微信信息的传播过程,提高信息监管的时效性,应当关注用户的信息临时免疫期时滞,以尽早采取措施应对Hopf分岔的产生。
