基于双质量水平的供应链动态时滞模型研究
2020-09-07吴选玉戴道明
吴选玉,戴道明
(安徽财经大学 1.物流与供应链管理研究中心,2.管理科学与工程学院,安徽蚌埠 233000)
随着产品种类的日益增多,消费者的选择范围变得越来越广泛,消费者在关注产品的价格之余,还关注产品的质量与零售商的服务质量。产品的质量水平对消费者的需求有着重要的影响,同时零售商的服务水平对产品的销量也有着不可忽视的作用。因此制造商对产品质量水平的选择以及零售商对服务质量水平有着非常重要的现实意义。
关于供应链中产品的质量水平问题,文献[1-2]分析了供应链中的产品质量控制问题。李胃胜等[3]探讨了在不完备质量下的供应链“质量水平—协调契约”机制及其最优策略问题。白世贞等[4]研究了在电子商务环境下,预售与现售两种模式下产品质量水平与价格影响需求的供应链协调问题。林晶等[5]基于stackblerg博弈模型,分析制造商在不同渠道下的产品质量水平的选择问题及定价决策。关于零售商服务质量水平的研究,吴晓研等[6]研究了物流服务供应链中的物流服务供应商的物流服务质量改进行为的激励机制和惩罚机制。何茜[7]研究了制造商的动态定价策略和服务质量策略。彭冬[8]以BD公司为研究对象,研究影响BD公司合作的第三方物流供应商服务质量的关键因素。张智勇等[9]在服务提供商服务质量已知的情况下,分析了养老服务集成商如何通过博弈获得最优质量决策的问题。关于将产品质量水平与零售商服务质量水平进行结合研究,何娟等[10]分析了供应商的风险规避行为对其生产决策以及供应链协调条件的影响。另外还有学者考虑制造商提供免费质量保证服务,零售商提供付费的可选质量保证服务的供应链最优决策问题[11]。郑斌等[12]分别研究了制造商与零售商单独提供服务以及二者同时提供服务的双渠道供应链最优定价问题。
综上所述,现有关质量水平方面的文献主要是关于产品质量水平与服务质量水平的单方面静态研究,关于产品质量水平与服务质量水平的联合动态研究并不多见,因此本文在已有文献研究成果的基础上,将产品质量水平与服务质量水平同时引入供应链,分别研究了静态供应链的协调性以及最优决策问题和动态时滞模型的系统稳定性问题。
1 符号说明与假设
本文基于单制造商与单零售商所构成的供应链,制造商负责产品的生产,然后将商品批发给零售商进行销售,零售商在销售商品的过程中向顾客提供相应的售前服务以期增加销量。
参变量说明:制造商以批发价w将商品批发给零售商,零售商以零售价P进行零售,单位产品的生产成本为c;决策变量说明:产品的质量水平为Q,零售商的服务质量水平为S。
本文的主要假设如下:
(1)制造商与零售商在静态单周期情形是完全理性的,在动态情形下是有限理性的。
(2)假设需求期望[13]D=α-βP+ηQ+θS,其中,α为产品最大潜在需求量,β为价格敏感系数,η为质量水平敏感系数,θ为服务质量水平敏感系数。
(3)仅考虑一次性资金投入的情况,制造商要让产品质量水平达到Q,需要支付的成本为kmQ2/2,km为产品质量水平的成本系数,制造商其他成本均忽略;零售商要让服务质量水平达到S,需要支付的成本为krS2/2,kr为服务质量水平的成本系数,零售商其他成本均忽略。
(4)为了确保制造商和零售商能正常获利,设定P>w>c。
(5)消费者具有质量水平偏好,所以对制造商的产品水平和零售商的服务质量水平均颇为敏感。
(6)假设周期内零售价、批发价是固定不变的
2 供应链协调决策模型的建立
2.1 集中决策
集中决策下的供应链系统的利润为
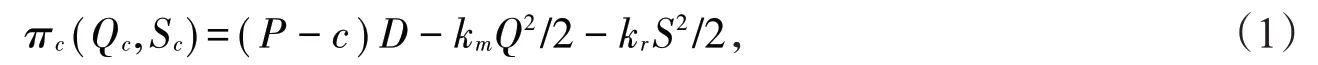
其中,πc代表集中决策下的系统利润,下标c表示集中决策。
在集中决策下,因为πc(Qc,Sc)是关于Qc,Sc的联合凹函数,因此计算可得:
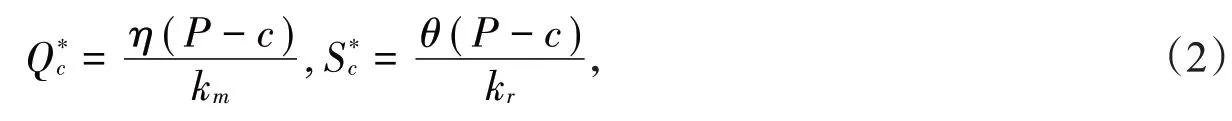
2.2 分散决策
分散决策下,制造商是领导者,零售商在制造商决策的基础上进行决策

其中,πd.m和πd.r分别代表制造商与零售商的利润,下标d代表分散决策。
由于制造商是占主导地位,因此制造商首先做出决策。运用逆向求解法,先求解零售商最优决策,πd.r是关于Sd.r的严格凹函数,可得

再求解制造商最优决策。把(5)式代入(3)式,根据海瑟矩阵可知πd.m是关于Qd的严格凹函数,故:

将(5)、(6)式带入(3)、(4)式可得:
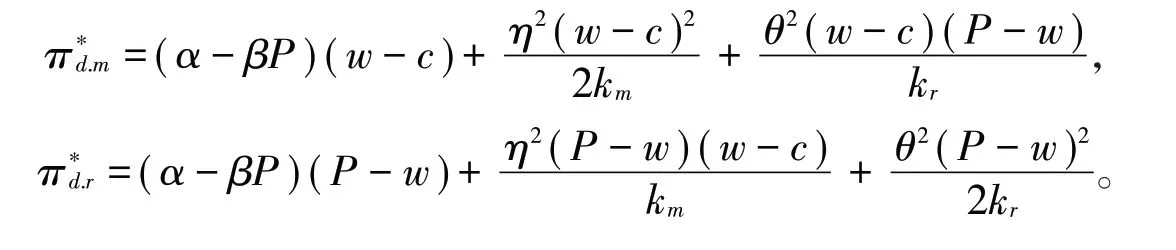
2.3 均衡解的比较
命题1集中决策下的产品质量水平大于分散决策下的产品质量水平,集中决策下的零售商服务质量水平大于分散决策下的服务质量水平,集中决策下的供应链利润要高于分散决策下的供应链利润。
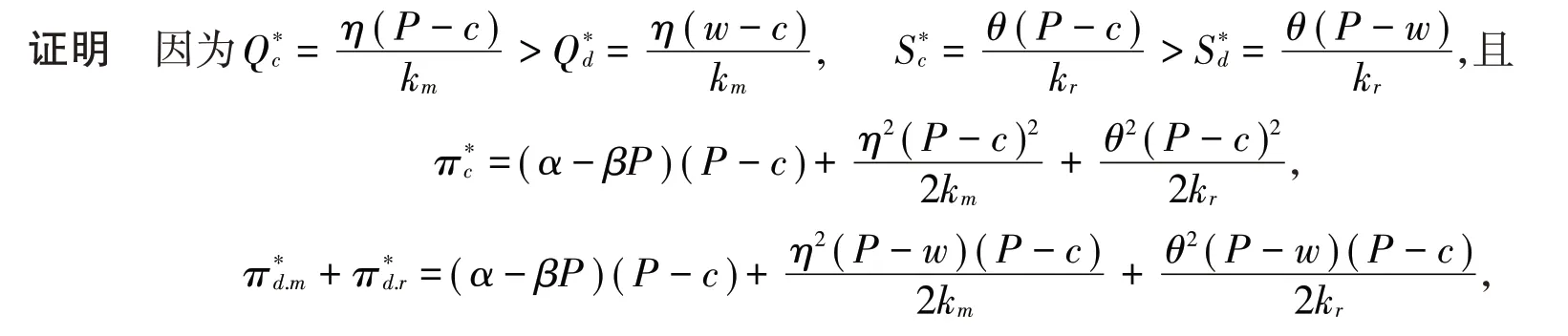
命题1表明:集中决策下的供应链效率要高于分散决策下的效率,即分散决策下存在效率的缺失。具体表现为产品质量水平投入和零售商的服务质量水平投入均不足,从而导致利润的减少。这是因为在现实生活中,制造商与零售商是相对独立的经济个体,所以无法避免低效率的工作方式。正如科斯定理所描述的,供应链各级主体在追求各自利润最大化的过程中,由于存在外部性,所以导致效率降低。
3 时滞动态模型构建
由于信息的不对称性,制造商与零售商很难在掌握全面信息的基础上进行决策,并且单周期静态研究只能反映供应链在某一个周期内的变化情况,前文的单周期静态供应链协调研究难以描述供应链的真实特征,因此本文通过建立动态时滞模型,从多周期的角度去研究供应链各方主体的决策问题,边际利润是制造商与零售商进行决策调整的重要依据,零售商与制造商的边际利润表达式如下:
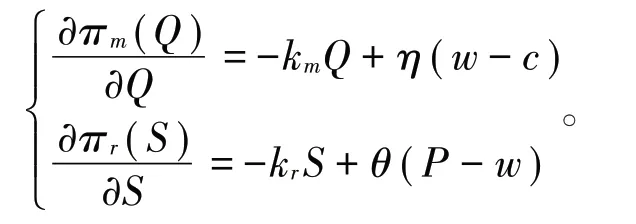
边际利润直接影响制造商和零售商的决策,当边际利润为正,制造商会提高产品的质量水平,零售商会提高服务质量水平;相反的,当边际利润为负,制造商会相应地降低产品质量水平,零售商也会降低服务质量水平。产品质量水平Q与服务质量水平S的动态过程[13]为
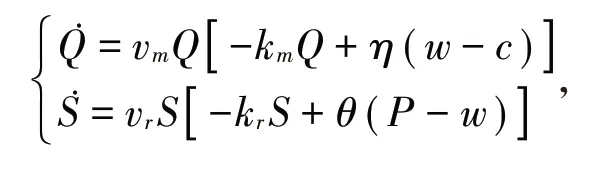
其中vm、vr分别是产品质量水平、服务质量水平调整速度。制造商和零售商可以根据现在市场的状况以及对未来市场预测的一些信息来进行决策,但是信息具有时滞性,本文在文献的基础上,考虑带有时滞性的供应链质量调整动态模型[14-15]:
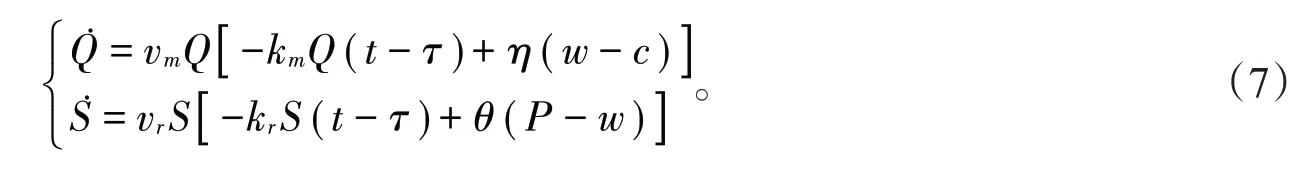
4 Hopf分岔的存在性和局部稳定性
经计算,模型(7)存在唯一的正均衡点E(Q*,S*),其中进而可以得到该模型在正均衡点E(Q*,S*)的特征方程为
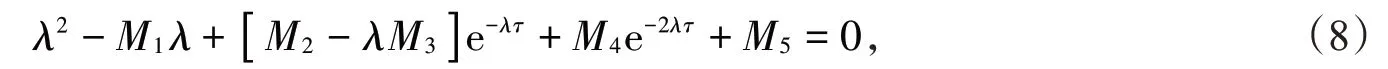
其中:M1=(a11+a22),M2=a11a34+a22a31,M3=(a31+a34),M4=a31a34,M5=a11a22,a11=-vmkmQ*+vmΔ1,

当τ=0时,方程(8)变为λ2+λ(-M1-M3)+M2+M4+M5=0,由劳斯-赫尔维茨稳定性判据可得,若条件(H1):(-M1-M3)>0,(M2+M4+M5)>0成立,则模型(7)在正均衡点处是局部渐近稳定的。
当τ>0时,令特征方程(8)等式两边同乘以eλτ,可得:
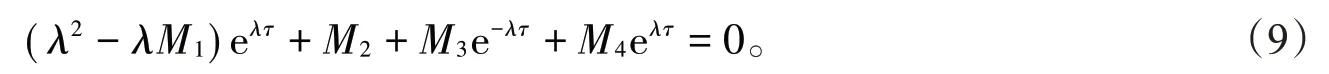
假定λ=iω(ω>0)是(9)式的一个正根,则有
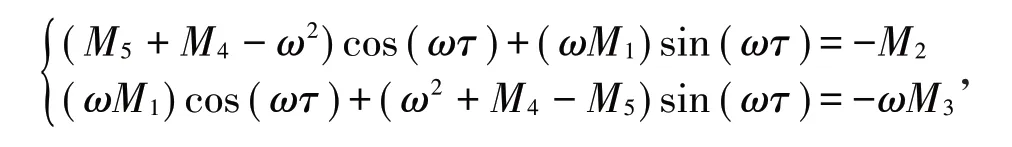
从而有
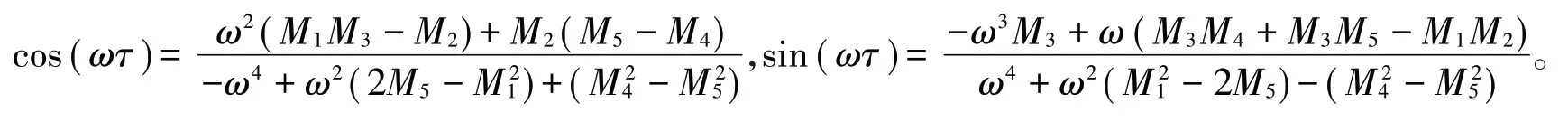
于是可以得到关于ω的代数方程式:ω8+ω6N1+ω4N2-ω2N3+N4=0,其中:
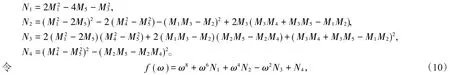
类比文献[12],作假设(H2):(10)式至少有一个正根。
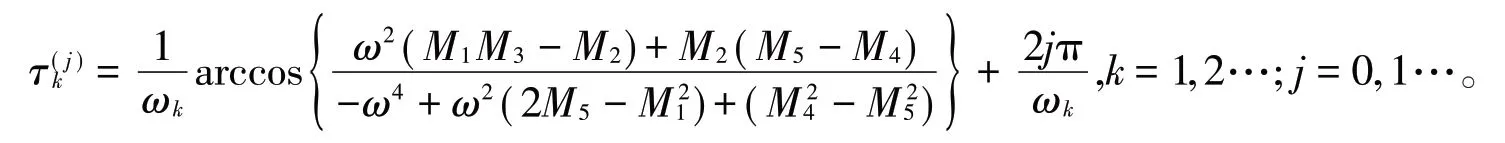
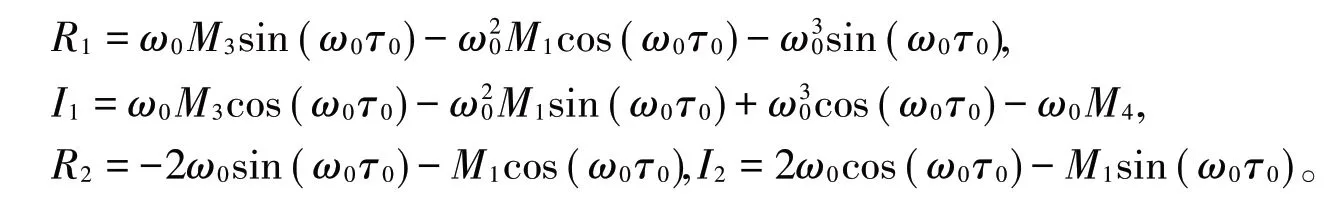
当条件(H3):R1R2+I1I2≠0成立,则模型(7)满足Hopf分岔的横截性条件,可得出以下结论[13]:
定理1对于模型(7),如果条件(H1)-(H3)均成立时,当τ∈[0,τ0),模型(7)在正均衡点E(Q*,S*)处局部渐近稳定;当τ=τ0时,模型(7)在均衡点E(Q*,S*)处产生分岔;τ>τ0时,模型(7)在均衡点E(Q*,S*)处是不稳定的。
5 数据模拟仿真
为了验证上述理论的正确性,取η=θ=0.4,km=kr=2,P=3,w=2,c=1,
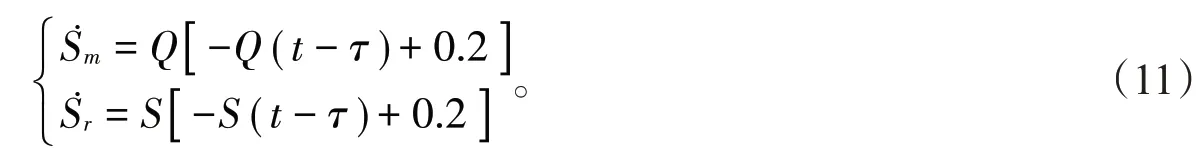
模型(11)的唯一正均衡点E*=(0.2,0.2),(-M1-M3)>0,(M2+M4+M5)>0,即模型(11)在正均衡点处渐近稳定。进而计算可得ω0=0.04,τ0=7.314。当τ=6∈[0,τ0)时,如图1所示,模型(11)是渐近稳定的;当τ=7.5>τ0时,如图2所示,模型(11)产生Hopf分岔,失去稳定性。从图1可以看出,模型(11)随着τ的增大逐渐由稳定产生Hopf分岔,然后转变为不稳定状态,且分岔临界点为τ0。因为模型(7)进入不稳定状态会导致价格与产品质量水平的剧烈波动,不利于制造商和零售商决策,所以制造商和零售商在面临决策问题时,所参照的历史信息要适当,过于久远的历史信息往往会使决策陷入不稳定状态。
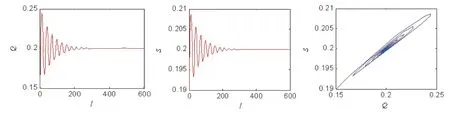
图1 当τ=6∈[0,τ0 )时系统渐进稳定
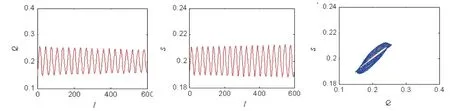
图2 当τ=7.5>τ0模型失去稳定性并产生Hpof分岔
由于在现实供应链竞争当中,制造商与零售商需要根据市场和竞争对手的决策信息来进行决策,过于延迟的决策以及过快的决策都会使得决策主体丧失最佳决策时机。因此制造商与零售商在进行价格决策时,不应该为了获得更大的利润而过于保守和盲目地提高价格决策速度,反而应该根据市场的状况以及竞争对手的决策进行综合考虑。
6 结 论
本文在已有研究的基础之上,联合考虑供应链中产品质量水平与零售商的服务质量水平。首先构建静态单周期供应链协调决策模型,分别给出了集中决策与分散决策下制造商与零售商的最优质量水平策略,并对集中决策下的最优决策与分散决策下的最优决策进行了对比分析;其次分析了动态时滞模型,探讨了系统的局部渐进稳定性以及Hopf分岔的存在性,并得出系统稳定的条件。研究表明,在满足一定条件的情况下,静态模型存在最优质量水平决策。同时还发现,制造商的产品质量水平与零售商的服务质量水平的决策延迟不宜过大,当τ∈[0,7.314 )时,系统在均衡点处渐进稳定;当τ>7.314时模型失去稳定性并产生Hpof分岔。因此制造商与零售商的质量水平决策所参照的历史信息不宜久远,否则会导致系统的失衡。出于简化模型的考虑,本文的研究仅考虑了供应链中零售商的服务质量水平,后期将进一步的研究可以共同考虑制造商与零售商的服务质量水平的模型。
