不容小觑的“填空压轴题”

康海芯

各地的中考数学试题中填空题的最后一道题，因为考查的背景新颖鲜活，涉及的知识点多，更侧重数学知识和数学思想方法的灵活运用，已然成为一类不容小视的压轴题。这就要求我们有较强的理解、分析和解决问题的能力，为帮助大家掌握填空压轴题的命题特点和解题策略，老师将结合2019年的部分中考试题加以分析，供大家参考。

一、探究最值型

例1（2019·江苏南通）如图1，?ABCD中，∠DAB=60°，AB=6，BC=2，P为边CD上的一动点，则PB+23PD的最小值等于。

【解析】如图2所示，题中已知B、D是两个定点，点P在CD上运动，延长AD至E，可知∠PDE=60°。要得到长为23PD的线段，只要过点P作PE⊥AD，交AD的延长线于点E，即可构造Rt△PDE，可得EP=23PD，即PB+23PD=PB+PE。要得PB+PE的最小值，只要点B、P、E三点共线且BE⊥AD，那么要求的最小值即为BE的长。在Rt△ABE中，AB=6，∠BAE=60°，依据BE3sin∠A=AB，解得BE=33，即PB+2PD的最小值为33。

【点评】解答这类最值问题时，常用的方法是构造直角三角形，把两条线段之和最值的问题转化为点到直线的距离问题。

二、图形变换型

例2（2019·江苏盐城）如图3，在平面直角坐标系中，一次函数y=2x-1的图像分别交x、y轴于点A、B，将直线AB绕点B按顺时针方向旋转45°，交x轴于点C，则直线BC的函数表达式是。

【解析】根据已知条件无法直接求出直线BC的函数表达式，结合题中∠ABC=45°联想到构造等腰直角三角形，即过A作AF⊥AB交BC于F，得到AB=AF，随后求出点F的坐标即可。过F作FE⊥x轴于E，根据全等三角形的性质得到AE=OB=1，EF=OA=2，求得F（2，-2），最后利用待定系数法即可求出直线BC的函数表达式为y=13x-1。

【点评】解答这类图形变换问题时，若题中出现直角三角形和45°两个条件时，我们可以考虑作垂线构造“一线三直角”模型，利用全等三角形或相似三角形的性质来求解。

例3（2019·江苏扬州）如图5，在△ABC中，AB=5，AC=4，若进行以下操作，在边BC上从左到右依次取点D1、D2、D3、D4......过点D1作AB、AC的平行线分别交AC、AB于点E1、F1;过点D2作AB、AC的平行線分别交AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交AC、AB于点E3、F3......则4（D1E1+D2E2+...+D2019E2019）+5（D1F1+D2F2+...+D2019F2019）=。

【解析】根据题中条件D1F1∥AC，D1E1∥AB，利用平行线分线段成比例定理D1F1BF1D1F1AB-D1E1可得AC=AB，即AC=AB。因为AB=5，AC=4，则有4D1E1+5D1F1=20;同理有如下规律4D2E2+5D2F2=20，......，4D2019E2019+5D2019F2019=20，因此4（D1E1+D2E2+...+D2019E2019）+5（D1F1+D2F2+...+D2019F2019）=20×2019=40380。

【点评】解答这类规律探究问题时，我们常用的方法是由特殊出发，多算几组线段的长，多比较几组数，发现循环组，即可快速找到解决思路。

例4（2019·江苏常州）如图6，在矩形ABCD中，AD=3AB=310，点P是AD的中点，点E在BC上，CE=2BE，点M、N在线段BD上。若△PMN是等腰三角形且底角与∠DEC相等，则MN=。

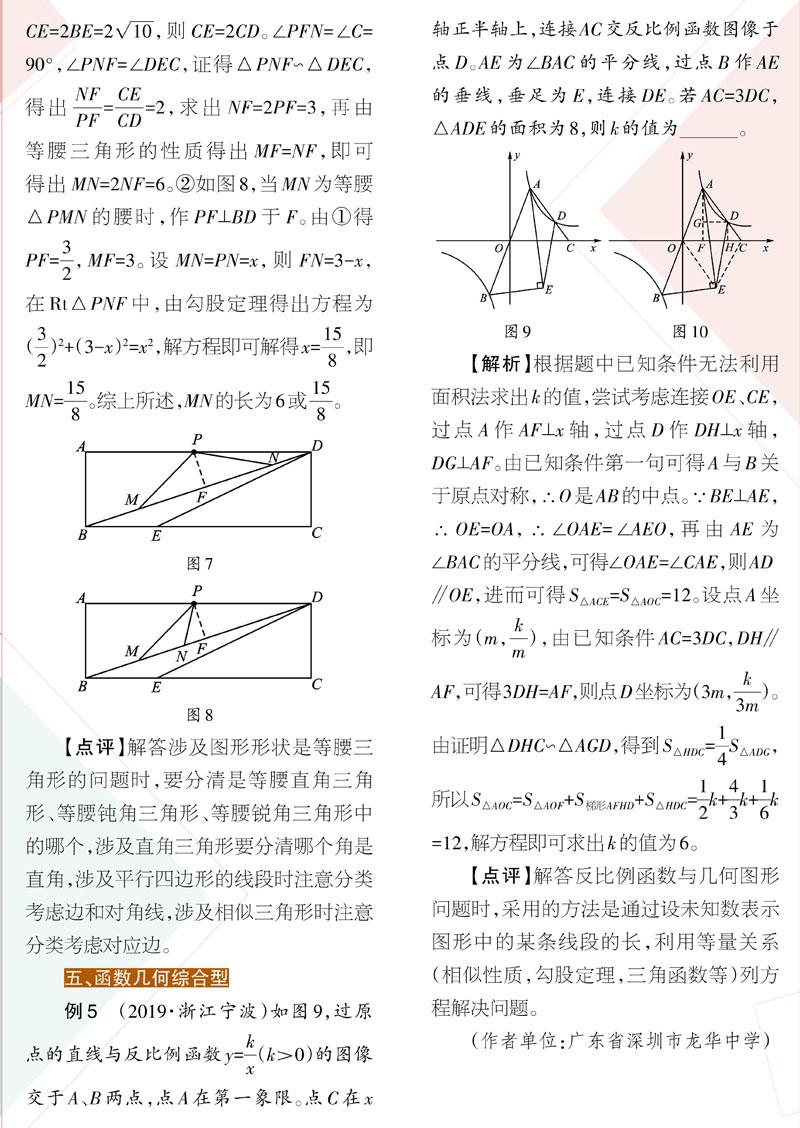
【解析】题中M、N在线段BD上，但位置没有指明，而△PMN是等腰三角形且底角与∠DEC相等，则应考虑分类讨论求解，即分以下两种情况。1如图7，当MN为等腰△PMN的底边时，作PF⊥MN于F，则∠PFM=∠PFN=90°。由矩形的性质得出AB=CD，BC=AD=3AB=310，∠A=∠C=90°，得出AB=CD=10，BD=AB2+AD2=10。证明PFPD3△PDF∽△BDA，得出AB=BD，求出PF=2。CE=2BE=210，则CE=2CD。∠PFN=∠C=90°，∠PNF=∠DEC，证得△PNF∽△DEC，得出NF=CE=2，求出NF=2PF=3，再由PFCD等腰三角形的性质得出MF=NF，即可得出MN=2NF=6。2如图8，当MN为等腰△PMN的腰时，作PF⊥BD于F。由1得PF=32，MF=3。设MN=PN=x，则FN=3-x，在Rt△PNF中，由勾股定理得出方程为（3）2+（3-x）2=x2，解方程即可解得x=15，即MN=15。综上所述，MN的长为6或15。

【点评】解答涉及图形形状是等腰三角形的问题时，要分清是等腰直角三角形、等腰钝角三角形、等腰锐角三角形中的哪个，涉及直角三角形要分清哪个角是直角，涉及平行四边形的线段时注意分类考虑边和对角线，涉及相似三角形时注意分类考虑对应边。

五、函数几何综合型

例5（2019·浙江宁波）如图9，过原点的直线与反比例函数y=x（k>0）的图像交于A、B两点，点A在第一象限。点C在x轴正半轴上，连接AC交反比例函数图像于点D。AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连接DE。若AC=3DC，△ADE的面积为8，则k的值为。

【解析】根据题中已知条件无法利用面积法求出k的值，尝试考虑连接OE、CE，过点A作AF⊥x轴，过点D作DH⊥x轴，DG⊥AF。由已知条件第一句可得A与B关于原点对称，∴O是AB的中点。∵BE⊥AE，∴OE=OA，∴∠OAE=∠AEO，再由AE为∠BAC的平分线，可得∠OAE=∠CAE，则AD∥OE，进而可得S△ACE=S△AOC=12。设点A坐标为（m，k），由已知条件AC=3DC，DH∥AF，可得3DH=AF，则点D坐标为（3m，）。由证明△DHC∽△AGD，得到S△HDC=4S△ADG，所以S=S+S+S=1k+4k+1k=12，解方程即可求出k的值为6。

【点评】解答反比例函数与几何图形问题时，采用的方法是通过设未知数表示图形中的某条线段的长，利用等量关系（相似性质，勾股定理，三角函数等）列方程解决问题。

（作者单位：广东省深圳市龙华中学）

初中数学规律探索问题是数学学习中常见的一类题型，也是近年来中考数学的热点题型。就其形式而言有数式、图形、数形结合等方式。下面，老师就以数式型规律探索题为例，谈谈解答技巧。

例1（2019·湖北武汉）观察等式：2+22=23-2;2+22+23=24-2;2+22+23+24=25-2......已知按一定规律排列的一组数：250、251、252......299、2100。若250=a，用含a的式子表示这组数的和是（）。

A.2a2-2aB.2a2-2a-2

C.2a2-aD.2a2+a

【分析】我们要通过观察，分析、归纳其中的规律，并应用发现的规律解决问题。解决本题的难点在于得出规律：2+22+23+...+2n=2n+1-2。那么250+251+252+...+299+2100=（2+22+23+...+2100）-（2+22+23+...+249），将规律代入计算即可。

解：∵2+22=23-2;2+22+23=24-2;2+22+23+24=25-2......

∴2+22+23+...+2n=2n+1-2，∴250+251+252+...+299+2100=（2+22+23+...+2100）-（2+22+23+...+249）=（2101-2）-（250-2）=2101-250，∵250=a，∴2101=（250）2·2=2a2，

∴原式=2a-a。

故选C。

例2（2019·山东济宁）已知有理数a=?1，我们把1称为a的差倒数，1-a如：2的差倒数是1=-1，-1的差倒数是1-（-1）=2。如果a1=-2，a2是a1的差111-2倒数，a3是a2的差倒数，a4是a3的差倒数......依此类推，那么a1+a2+...+a100的值是（）

【分析】解决本题，我们要通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况。求出数列的前4个数，从而得出

这个数列以-2，1，3依次循环，且-2+131323+2=-6，再求出这100个数中有多少个周期，从而得出答案。

解：∵a=-2，∴a=1=1，a=121-（-2）33

A.-7.5B.7.5C.5.5D.-5.5

1=3，a=1=-2......

1-13241-32

13∴这个数列以-2，，依次循环，

13132且-2+3+2=-6，

故选A。

例3（2019·湖南株洲）从-1，1，2，4四个数中任取两个不同的数（记作ak，bk）构成一个数组MK={ak，bk}（其中k=1，2......S，且将{ak，bk}与{bk，ak}视为同一个数组），若满足：对于任意的Mi={ai，b}i和Mj={aj，b}j（i=?j，1≤i≤S，1≤j≤S）都有ai+bi=?aj+bj，则S的最大值（）。

【分析】找出ai+bi共有几个不同的值是解题的关键。求出ai+bi的值，结合对于任意的Mi={ai，b}i和Mj={aj，b}j（i=?j，1≤i≤S，1≤j≤S）都有ai+bi=?aj+bj，即可得出S的最大值。

解：∵-1+1=0，-1+2=1，-1+4=3，1+2=3，1+4=5，2+4=6，

∴ai+bi共有5个不同的值。

又∵对于任意的Mi={ai，b}i和Mj={aj，b}j（i=?j，1≤i≤S，1≤j≤S）都有ai+bi=?

aj+bj，

∴S的最大值为5。

故选C。

例4（2019·贵州安顺）如图1，将从1开始的自然数按以下规律排列，例如位于第3行、第4列的数是12，则位于第45行、第7列的数是。

【分析】解决本题的关键是仔细观

察，探究规律，利用规律解决问题。观察图表可知第n行第一个数是n2，可得第45行第一个数是2025，再观察每一行数字的变化规律，从而推出

结果。

解：观察图表可知第n行第一个数是n2，

∴第45行第一个数是2025，

∴第45行、第7列的数是2025-6=2019。

故答案为2019。

例5（2019·海南）有2019个数排成一行，对于任意相邻的三个数，都有中间的数等于前后两数的和。如果第一个数是0，第二个数是1，那么前6个数的和是，这2019个数的和是。

【分析】解决本题的关键是明确题意，发现题目中数字的变化规律。我们可以根据题意写出这组数据的前几个数，从而依据数字的变化规律解决问题。

解：由題意可得，这列数为：0，1，1，0，-1，-1，0，1，1......

∴前6个数的和=0+1+1+0+（-1）+（-1）=0，

∵2019÷6=336...3，

∴这2019个数的和=0×336+（0+1+1）=2。

故答案为0，2。

例6（2019·安徽）观察以下等式：

......

按照以上规律，解决下列问题：（1）写出第6个等式：;（2）写出你猜想的第n个等式：

（用含n的等式表示），并证明。

【分析】解决本题的关键是根据已知等式得出2=1+1的规

2n-1nn（2n-1）律，并熟练加以运用。

解：（1）第6个等式为2=1+1。21111666

（2）=+。2n-1nn（2n-1）

证明：∵右边=1+1

nn（2n-1）

2n-1+1=2=左边。

n（2n-1）2n-1

∴等式成立。

故答案为2=1+

探索规律型试题体现了数学中的归纳、猜想的思考方法和转化的数学思想。根据条件中的信息，结合自己掌握的知识，做出一种可能存在的规律性的结论推断，这就是归纳、猜想的过程。解决这类问题的思路是从简单的、局部的、特殊的情形出发，经过提炼、归纳、猜想，寻找到一般的规律，从而解决问题。

（作者单位：江苏省南京市鼓楼实验中学）