漫谈证明

李福良

证明，主要指由已知事实或结论推理未知结论成立的过程。证明从哪来？为什么要证明？证明过程有哪些形式？

证明的由来

在人类历史上，“证明”这个想法是怎样产生的？又是什么时候产生的呢？

一般认为，数学证明开始于公元前6世纪。在距今2600多年前，希腊数学家和哲学家泰勒斯证明了几条几何定理。到了公元前4世纪，欧几里得撰写了不朽巨著《几何原本》。他从一些基本定义与公理、公设出发，以合乎逻辑的演绎手法推导出400多条定理，奠定了数学证明的模式基础。

可是，为什么当时的人会想到去证明数学命题呢？许多经过反复实践的直观易懂的数学命题，不需要解释就已经被人们所接纳了，比如对顶角相等、直径把圆平分等命题，难道还需要怀疑吗？为什么这么“浅显”的道理也有人去琢磨呢？

这就是证明的魅力所在。

证明不仅仅在于说服别人相信结果的正确性，更反映了推理过程的严谨性。这也是数学的魅力所在。

美国前总统亚伯拉罕·林肯曾是一名律师，他的身边常伴有《几何原本》。他经常将其拿出来阅读并研究，直到熟练证明前6卷中的所有命题。他认为书中的演绎证明可以使自己的思维变得严谨、缜密，表达条理清楚，对他的职业有帮助。清朝康熙皇帝也在满文版的《几何原本》上留有学习时所做的笔记。

证明的必要性

在几何中，除了公理以外，不论所讨论的命题的结论有多么明显，这些命题都必须通过推理来证明。为什么呢？这是因为，首先，直观的结论有时会造成错觉，并不永远可信;其次，对少数具体例子进行观察、测量得出的结论，并不能保证所有情况下都成立。

例如，在17世纪，法国数学家费马曾研究过22n+1这个代数式，当n=0、1、2、3、4时，22n+1对应的值分别为3、5、17、257、65537，都是质数（质数是在大于1的自然数中，除了1和它本身以外，不再含有其他因数的数）。当n=5时，22n+1的数值太大，他没有计算，于是他便猜测：对于一切自然数n，22n+1都是质数。然而，费马去世后若干年，瑞士数学家欧拉证明，当n=5时，22n+1=641×6700417，是一個合数。

再比如，图形的性质不能通过测量得出，如平行线永不相交，这就无法测量。此外，通过推理研究图形，可以揭示图形性质之间的联系，比如两直线平行，同位角、内错角、同旁内角之间存在关系。

因此，证明是必要的。

证明的趣味性

在19世纪，有一个农场主，他养猪总是养不胖。于是，他就向生物学家、博物学家达尔文请教。达尔文告诉农场主要多养猫，理由是：猫吃田鼠，田鼠吃土蜂，土蜂给三叶草传粉;土蜂多了，三叶草便生长得旺盛，而猪吃三叶草，饲料多了，猪就会胖起来。

这就是生物学家眼中的推理。同学们，生活中的推理无处不在。

我们再看一个有趣的证明，请看下列图形：

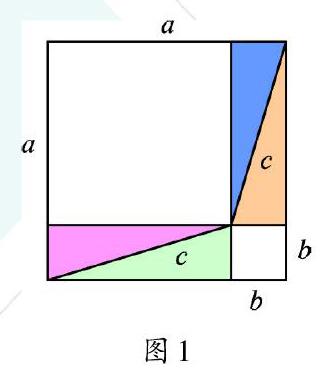
从图1到图2，都是一个大正方形，里面有4个相同的彩色直角三角形。在这里，相同的图形用不同的拼接方式，就能说明a2+b2=c（2两个图形中，白色部分的面积相等）。这就是著名的“勾股定理”。

用图形语言就可以表达经典的结论，这种证明方法叫作“无字证明”。

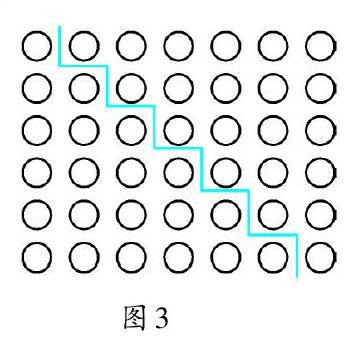
聪明的你，现在观察图3，能得到什么结论呢？

（作者单位：江苏省扬州市江都区教育局教研室）