基于硅-玻璃键合工艺的微惯性器件的材料热失配应力表征
2020-09-05刘梦霞董显山赵前程
刘梦霞,秦 强,董显山,崔 健,赵前程*
(1. 北京大学微米/纳米加工技术国家级重点实验室,北京 100871;2. 工业和信息化部电子第五研究所 电子元器件可靠性物理及其应用技术国家级重点实验室,广东 广州 510610)
1 引 言
硅基微机电系统(Micro-Electro-Mechanical System,MEMS)惯性传感器具有小体积、低功耗、低成本等显著优势,已广泛应用于军事和民用领域[1-2]。微加工艺是MEMS惯性传感技术的基础支撑技术,工艺误差是微惯性仪表各类关键误差的主要来源。基于硅-玻璃键合工艺实现敏感结构和衬底相接是微惯性器件的主流工艺方案之一,美国Honeywell公司、挪威Sensonor公司以及日本Silicon sensing公司等都成功推出了基于硅-玻璃工艺的高精度MEMS陀螺产品。阳极键合作为硅-玻璃工艺的关键技术,可以有效地将硅与玻璃结合在一起[3-7]。由于阳极键合的两种材料硅和玻璃的热膨胀系数不一致,MEMS器件工作环境温度的变化会使得硅和玻璃两种材料拉伸或压缩的长度不同,从而在接触面产生跟温度相关的热失配应力。该应力通常在结构锚点处产生,会直接影响器件谐振频率的温度稳定性[8-9],严重影响器件的零位温度稳定性以及长期稳定性[10-13]。因此,测量异质材料间的热失配应力以及键合锚点尺寸对热应力的影响,对结构以及工艺设计改进具有重要的意义。
拉曼光谱法可直接对局部微小区域进行原位残余应力测量[14-20]。然而,由于硅和玻璃都具有一定的厚度,拉曼光谱法难以准确测量硅玻璃键合界面的热应力。此外,拉曼光谱法对应力测量的精度在10 MPa左右[21-22]。而对于MEMS惯性器件,其尺寸非常微小,1 MPa的应力便可以对结构造成不可忽略的影响[23]。因此,针对硅玻璃键合表面热应力测量需要一种测量精度更高更可行的方法。
为了更加直接而简便地表征热失配应力,本文通过测量结构形变的方法来分析器件锚点的表面应力。首先设计微悬臂梁作为辅助测试结构,使用COMSOL对它进行热应力仿真。在测试中,通过测量悬臂梁的翘曲程度来得到锚点应力受温度以及锚点自身的影响。为消除因表面工艺KOH腐蚀造成悬臂梁表面不平整带来的高度误差和测量随机性误差,对同一结构进行多次测量以及同时测量多组相同结构。将测量数据进行相应算法处理,以得到悬臂梁在热应力作用下相对锚点的离面位移(即悬臂梁与锚点两者平均高度之差)。
2 悬臂梁式锚点应力结构设计及原理
在测试结构设计中,结构越复杂,对应力产生影响的因素就越多,因此结构设计宜简单。悬臂梁结构的翘曲程度可以直观反应锚点应力,因此选取悬臂梁作为测试结构。图1为硅玻璃键合及形变示意图。其中图1(a)为测试结构示意图,下层衬底材料为玻璃,上层结构材料为硅。两者通过阳极键合结合在一起。结构几何参数见表1。锚点为水平截面为不同边长正方形的长方体,以研究锚点尺寸与热膨胀引起形变之间的关系。
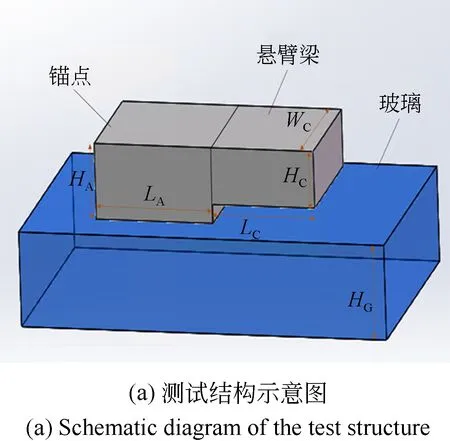
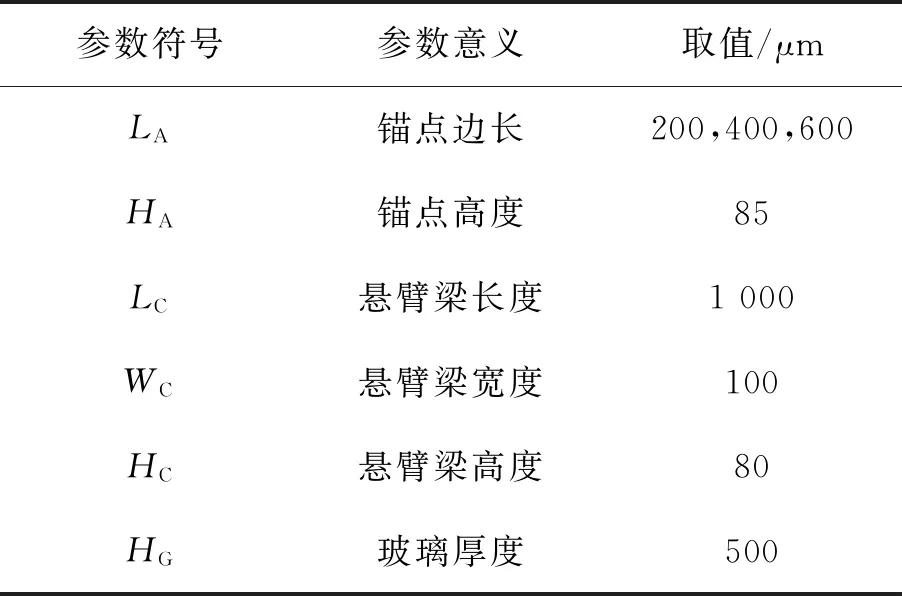
表1 悬臂梁式锚点应力测试结构的设计参数
当器件的环境温度发生改变,硅和玻璃的热膨胀系数不一致导致它们膨胀或收缩程度不同,在键合界面会产生应力。这种内应力使得锚点与玻璃发生凹凸变形,并且使锚点的侧壁发生倾斜,如图1(b)所示(这里只画出了结构左右方向的翘曲,实际前后方向也有相应的翘曲)。由于悬臂梁仅和锚点的侧壁相连,另一端完全自由,因此悬臂梁内部不会产生应力。故而设计较长的悬臂梁结构可以将锚点侧壁的倾斜放大为较明显的离面位移。这种离面位移直接反映了硅和玻璃的热膨胀变形情况以及接触界面的热失配应力。因此,需要准确测量悬臂梁的离面位移。
图1(c)是结构层硅发生形变后的示意图(彩图见期刊电子版)。图中实线部分为测试结构上表面形变示意图。O点为锚点与悬臂梁的接触点,N点为悬臂梁最远端,M点为悬臂梁中点。蓝色虚线所示高度为锚点平均高度,黄色虚线为高度参考线。可以得到关系式:h3=h1/2+h2。硅玻璃接触界面热失配应力可通过离面距离h3表征出来,因此选取h3作为实验测量目标。
3 仿真分析
本文采用有限元软件COMSOL进行仿真。首先对测试结构进行建模及网格划分,如图2(a)所示。下层衬底为玻璃,结构层为硅。锚点形状为正方形,其边长分别取600,400和200 μm。其余尺寸参数见表1。为减小上层结构形变以降低对器件性能的影响,可通过将锚点切分为多个边长为90 μm,间距为10 μm的正方形阵列的方式减小锚点的刚度,如图2(b)所示。
初始温度设置为30 ℃,目标温度点选择40 ℃。硅和玻璃材料参数选取如表2所示。

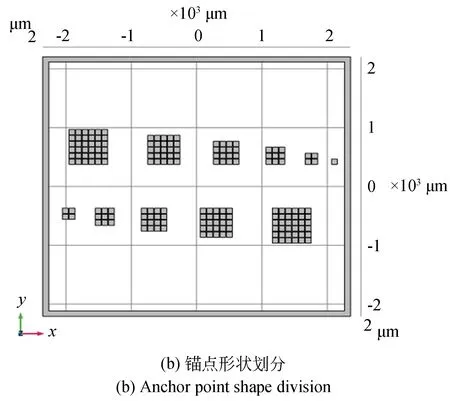
图2 悬臂梁式锚点应力测试模型示意图Fig.2 Schematic diagram of stress test model for cantilever beam anchor
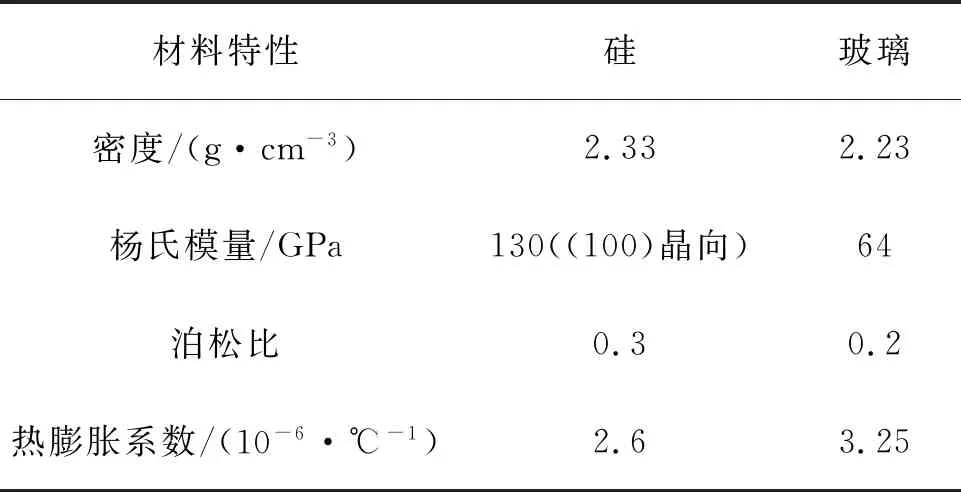
表2 硅与玻璃材料参数
图3为锚点进行切分后的仿真结果。从图3(a)中可以看出升温后各个部分z方向的位移变化。图3(b)显示了硅与玻璃接触面热失配应力分布。图3(c)为锚点不进行切分接触面热失配应力分布。对比图3(b)和3(c),锚点进行切分后最大应力可减小一半。表3是仿真数据的处理结果。其中,h1,h2和h3为锚点进行切分后得到对应高度,h3_2则为锚点不进行切分得到的离面距离。由表3数据可得,锚点越大,悬臂梁的翘曲值h1越大;锚点平均高度的绝对值|h2|越大;同时,测试结构的离面位移h3也越大。 比对h3_2和h3可知,锚点切分后离面位移减小,意味着热失配应力对器件性能的影响减小。
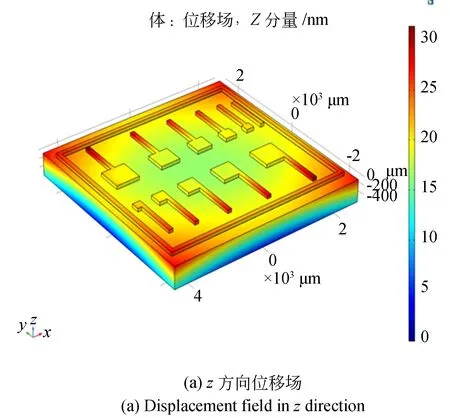
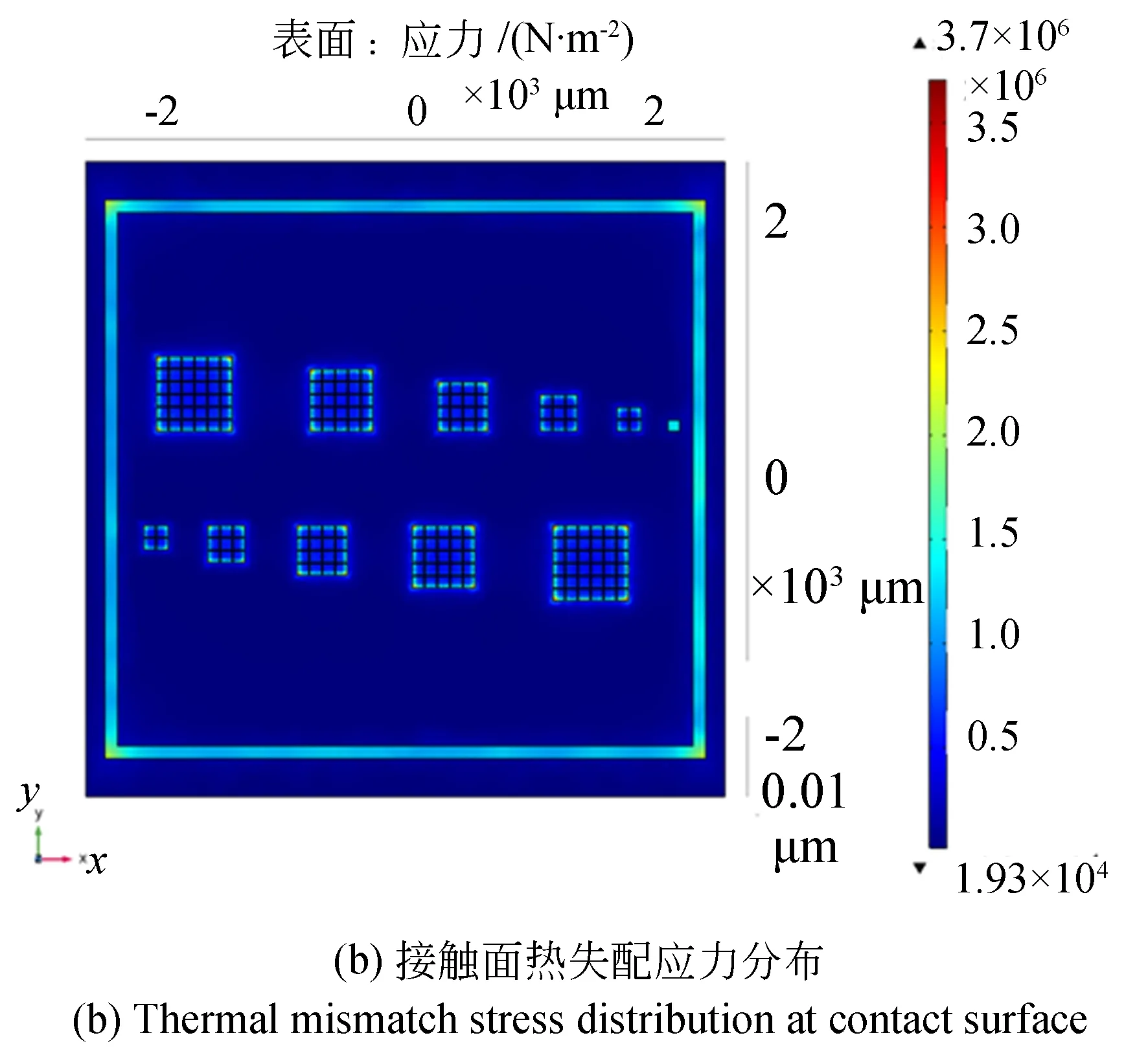
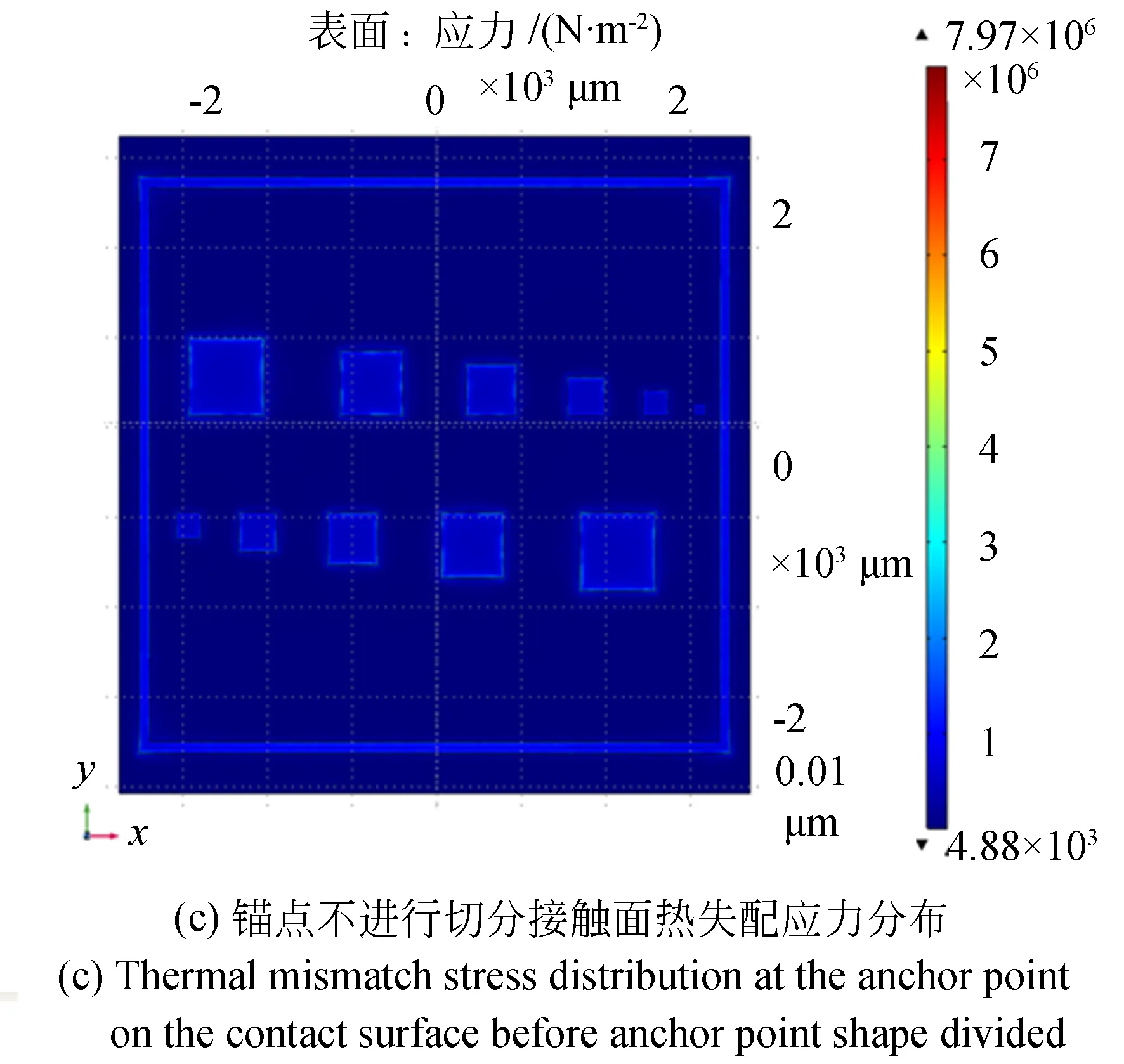
图3 仿真结果Fig.3 Simulation results
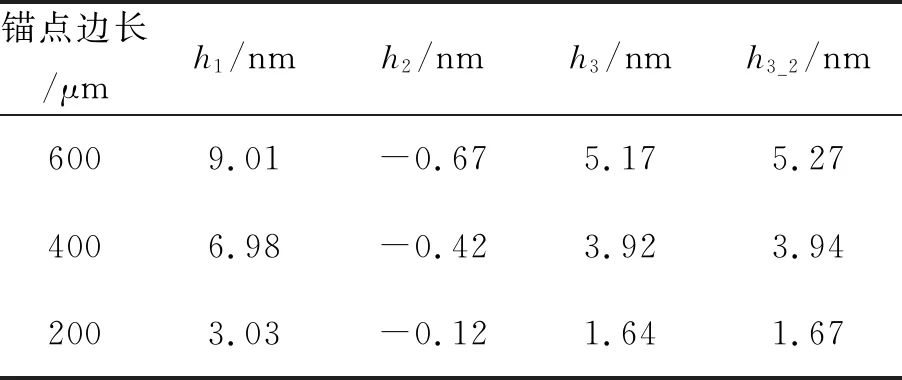
表3 测试结构仿真情况统计
4 锚点弯曲形变测试
4.1 测试方法
使用锚点切块的版图SOG(Silicon-on Glass)工艺加工测试结构。测试装备主要由控温装置和白光干涉仪组成。前者用于控制并稳定样品温度,后者用于对样品表面形貌的测量。
实际测量中会存在两个问题使得无法得到测试结构因热失配应力而产生的离面位移,如图4所示。图4(a)是400 μm锚点测试结构上的表面高度分布。图4(b)是(a)图中悬臂梁中线高度分布。图4(c)图则体现了对同一结构的两次测量结构会存在一定测量误差。
分析图4可知,测量的两个难题是:
(1)微结构上表面经过KOH减薄后会比较粗糙,大概有20 nm左右的起伏,这会一定程度上影响测量的准确性。从图4(c)可见测量随机性误差也不能被忽略。
(2)在图4(b)中,悬臂梁中线两端的高度差达高1 μm以上。这一差值并非完全由热失配应力所产生的离面位移引起,测试结构并非绝对水平放置和玻璃因温度改变而发生弯曲造成硅结构倾斜都对此有影响。因此,需要对数据进行后处理以提取因热失配应力而产生的离面位移。
对应上述两点提出以下解决方案:
(1)实验设置8组(编号为1~8)相同样品,每组样品各测量十次。以多次测量某一区域的位移取平均值作为测量指标。
(2)将测试所得的结构高度数据导入MATLAB进行处理提取悬臂梁相对锚点的离面距离。
测试中同一组样品位于同一芯片上。每组样品包含锚点边长为600,400,200 μm等不同结构参数的对比样品。
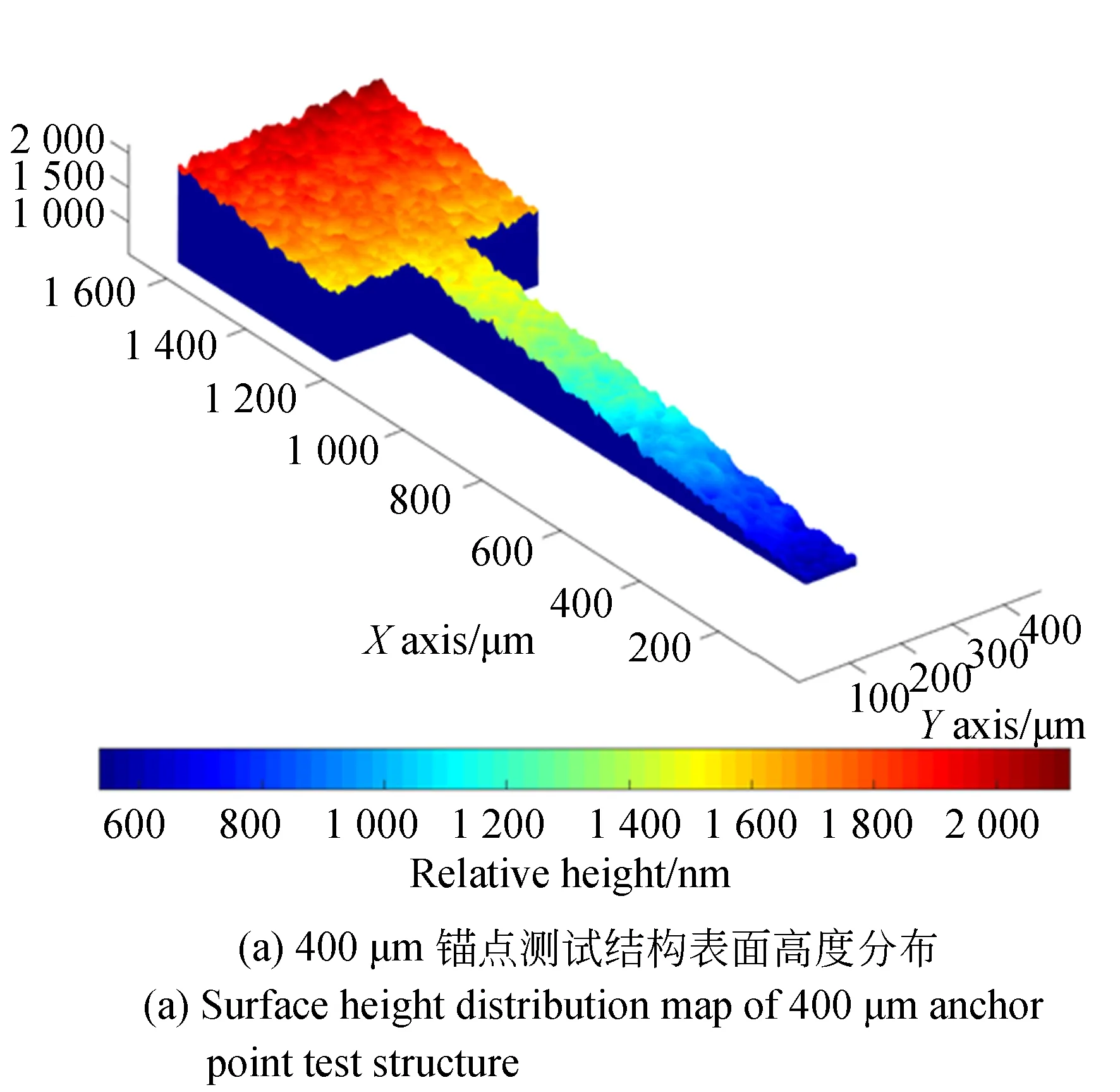
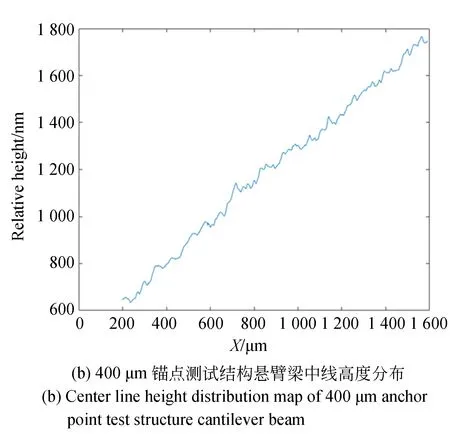
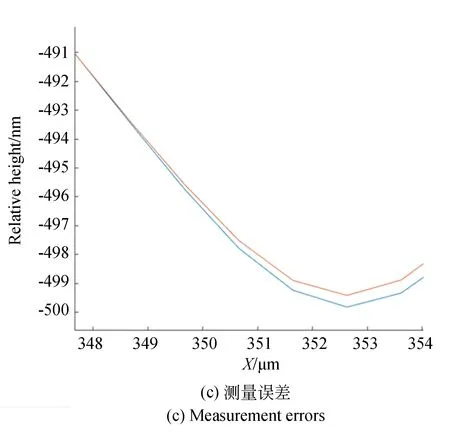
图4 测试中存在的问题Fig.4 Problems in the test
具体测试步骤如下:
(1)将芯片置于白光干涉仪下,调节仪器至PSI模式,并设定好仪器参数。
(2)调节温度控制装置,使样品温度达到60 ℃。为利于热量传递,每次调节温度后,需保证样品在稳定该温度下30 min后再做测量。
(3)温度稳定后每隔1 min对样品表面高度进行测量,共测量10次。
(4)以5 ℃为间隔,重复步骤(2)和(3)直到温度为30 ℃。
数据处理时以锚点平均高度为参考,测量整个悬臂梁的平均高度相对于锚点的平均高度之差。将采集到的离面位移的原始数据利用MATLAB工具进行处理,提取出所需结果。
数据处理步骤如下:
(1)先计算悬臂梁中线和锚点中线上各点的平均高度,得到两条离面位移分布曲线。
(2)将测试数据分为悬臂梁和锚点两个部分,分别进行曲线拟合。
(3)以悬臂梁和锚点交界处为轴,将锚点拟合曲线旋转至水平位置,图中其他曲线进行同一角度旋转。这样,保证了锚点表面的绝对水平,从而可提取悬臂梁因热失配应力而产生的离面位移。
(4)分别计算旋转后两条曲线的平均高度。
(5)两者平均高度之差即为悬臂梁相对锚点的离面位移。
(6)将十次测量得到离面位移取平均值,消除单次测量带来的误差。
(7)对八组样品所得的离面位移取平均值并计算标准值。
采用上述测量和数据处理方法,可以有效消除前述测量问题。
4.2 测试结果及数据分析
实际结构中,锚点段和悬臂梁段在交界处是连续的。但是在数据处理上,考虑到数据抖动等因素,这里以锚点平均高度为参考,测量整个悬臂梁的平均高度相对于锚点的平均高度之差。图5展示了第1,2组某次测试经数据处理过后的高度分布。图中横轴是沿悬臂梁中线的位置。其中,零点右侧为锚点部分,左侧为悬臂梁部分。纵轴是结构高度。悬臂梁部分的直线为各温度下的拟合直线,锚点部分的直线为锚点高度的平均值。图中以锚点平均值作为参考点,将各个温度下的锚点平均值画为同一条直线。其中,悬臂梁是用多项式最小二乘拟合方法拟合而得以还原其真实的翘曲情况,而锚点是各点高度取平均值,因此得到的这两段直线在图中表现不连续。为了使图形更美观清晰,此图仅展示了悬臂梁的测量高度差异最大的30 ℃和60 ℃两条曲线。
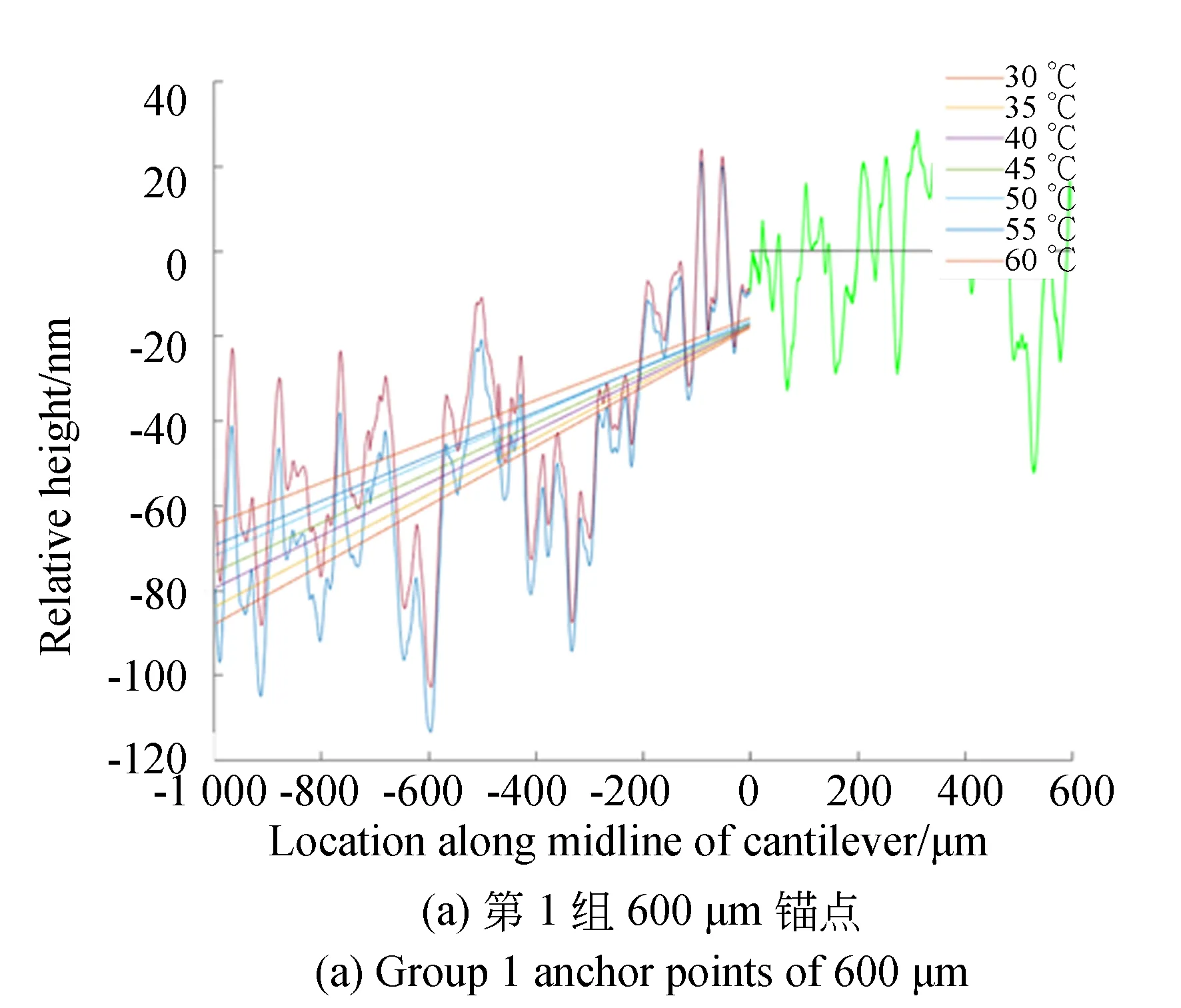
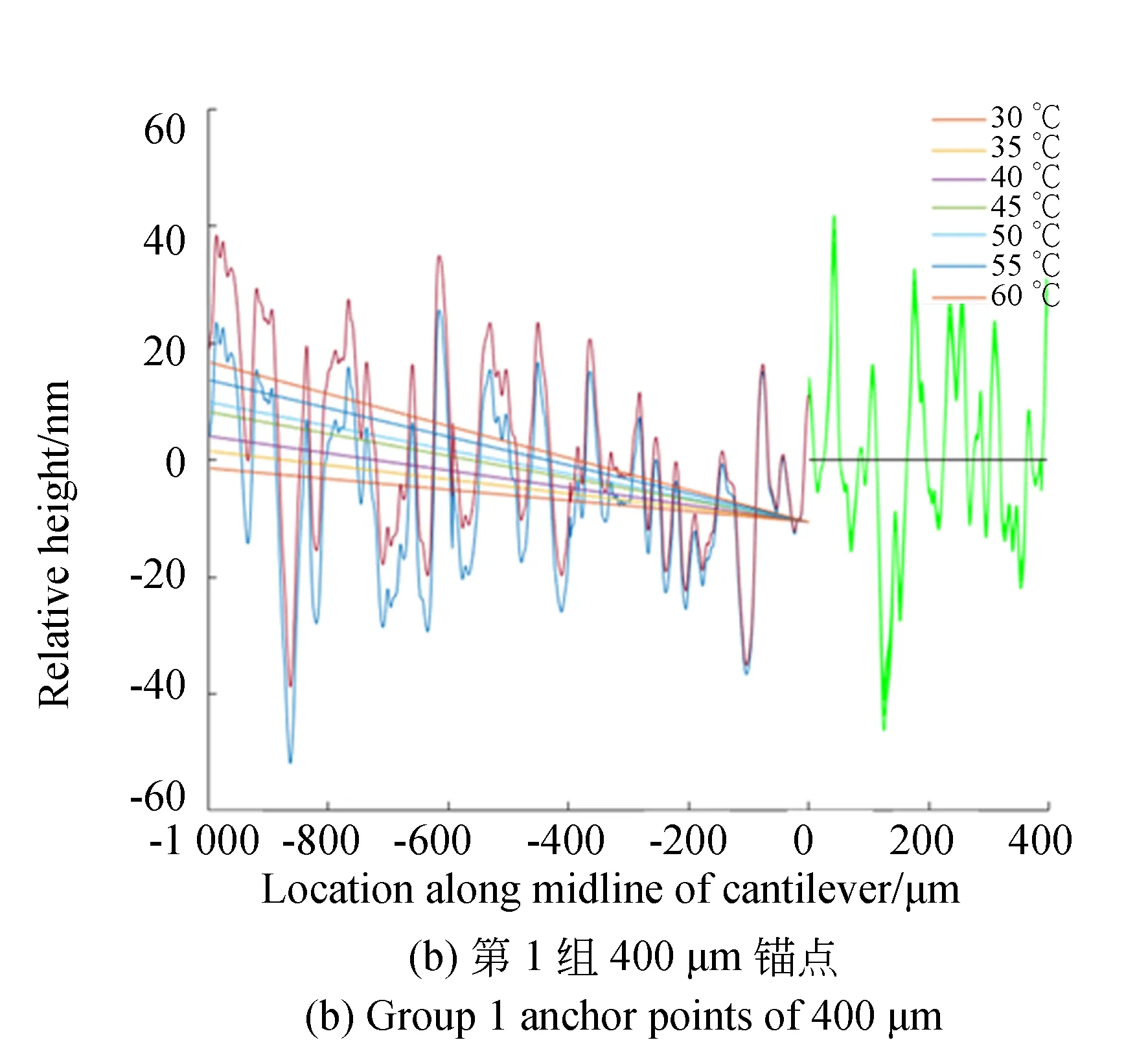
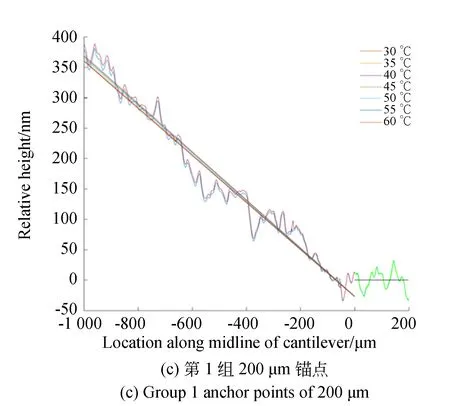

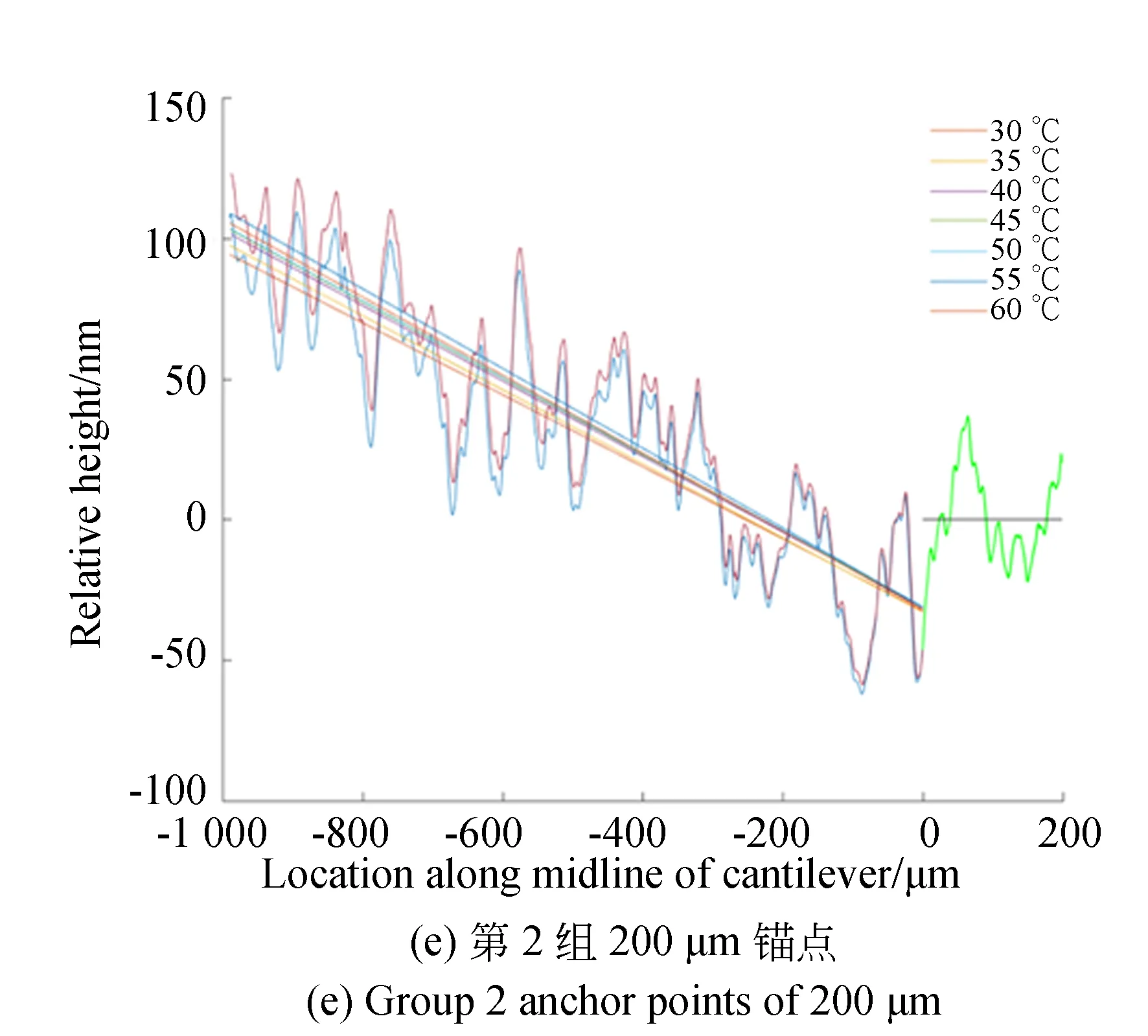
图5 数据处理后的高度分布Fig.5 Height distribution after data processing
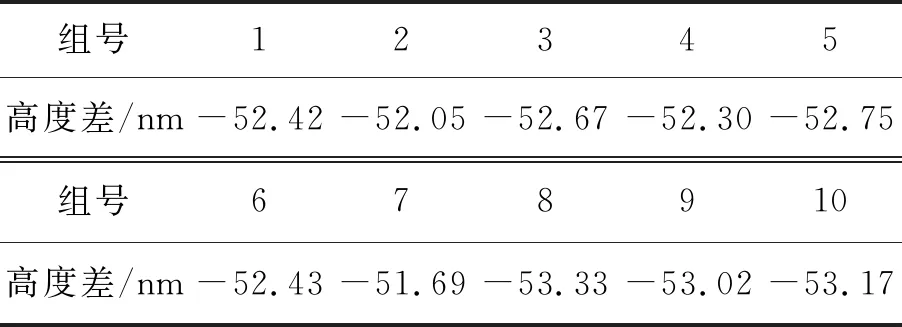
表4 第1组600 μm锚点测试结构在30 ℃下10次重复测量所得到的离面位移
表4统计了第1组600 μm锚点测试结构在30 ℃下10次重复测量所得到的离面位移。
由表4数据计算可得平均离面高度为-52.58 nm,标准差为0.510 3 nm。测量结果表现出很好的重复性。
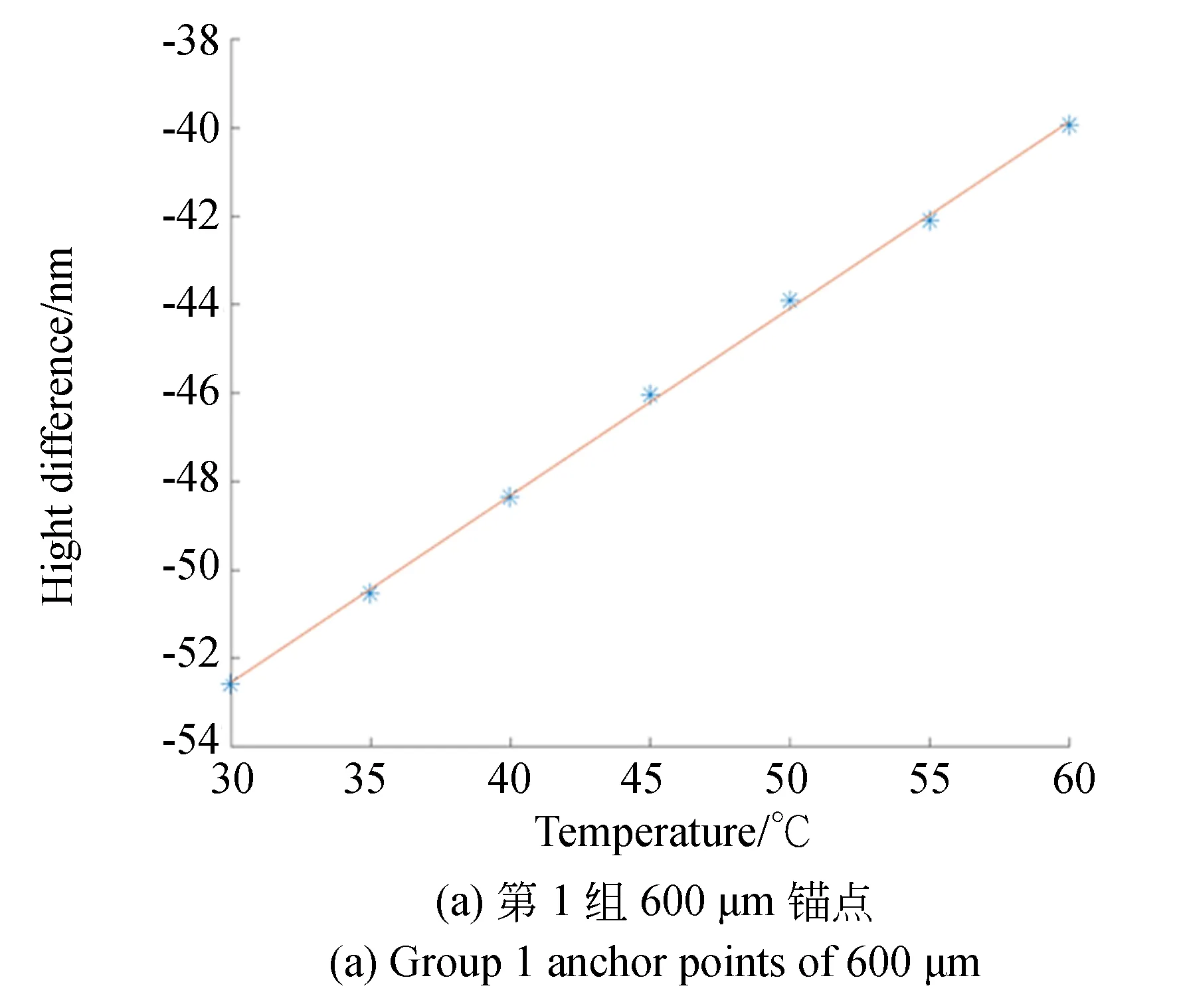


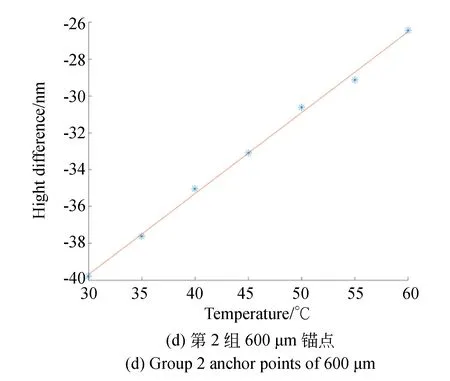
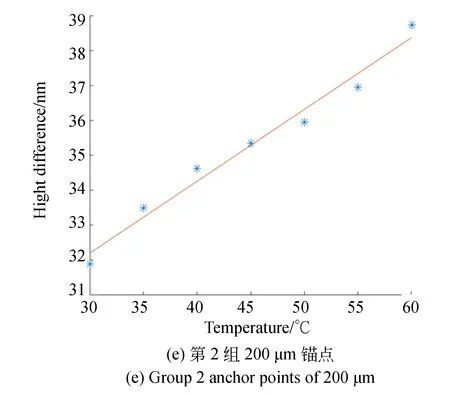
图6 测试结构在温变情况下的悬臂梁与锚点高度差Fig.6 Height difference between cantilever beam and anchor point of test structure at different temperatures
将每组10次测试得到的离面距离取平均值,画出每组平均离面位移与温度的关系。图6展示了第1,2组测试结构在温变情况下悬臂梁与锚点高度差的关系。图中直线为拟合结果,其斜率即为测试结构对温度的敏感度。
每组离面位移对温度的敏感度如表5所示。表6则是这8组数据的统计信息。重复性为温度敏感度的标准方差,标准方差越小,说明实验重复性越好。h3_test为由温度敏感度计算所得的30~40 ℃的离面位移。通过对比前面仿真得到的离面位移h3值,得到对比误差。
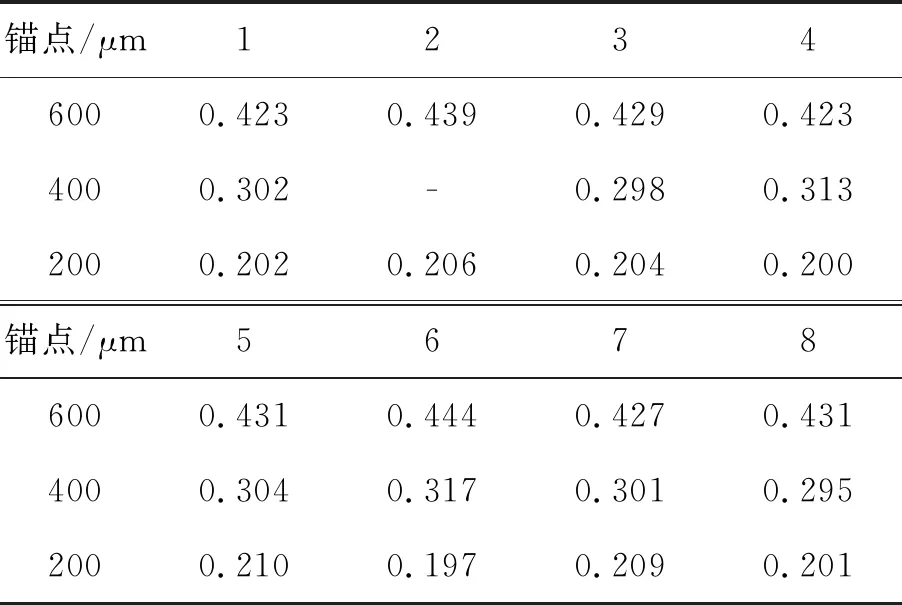
表5 8组样品离面位移对温度的敏感度

表6 8组样品离面位移对温度的分辨率统计数据
分析以上数据可得:
(1)该测试结果具有很好的重复性。标准方差均小于0.01 nm/℃。
(2)锚点越大,离面位移越大,意味着锚点热失配应力越大;而过小的锚点会使得器件结构容易断裂。此测试结果给器件锚点设计提供了参考。
(3)对比不同锚点的测试结果可以发现,大锚点重复性比小锚点更好。原因在于小锚点与衬底玻璃的结合程度不够好,在温度变化过程中,结合程度不够会带来更多随机性因素。
(4)比较仿真与测试结果可发现,对于400和600 μm锚点,实际测试的结果均比仿真值要小。这是因为在仿真中选取的硅的杨氏模量为130 GPa,而实际中硅的平均杨氏模量要大于这个值,故而结构整体弯曲刚度比仿真值要大,弯曲形变值也相应要小。另一方面,硅的热膨胀系数随温度逐渐增大,而玻璃的热膨胀系数则保持不变。温度升高时,两者的热膨胀系数差值减小,导致离面位移也减小,从而使直线斜率变小。
5 结 论
本文以悬臂梁作为测试结构,初步验证了一种锚点形变测量和数据处理方法的可行性,这为MEMS惯性器件结构形变的测试提供了一种新的思路。根据仿真结果,将测试版图的锚点切块以降低结构形变。测试结果具有良好的重复性,测试数据可进一步指示锚点热失配应力。同时,该结果也说明了锚点热形变与锚点的尺寸直接相关,这对MEMS惯性结构以及工艺设计改进具有重要意义。
