超大视场长波红外立体视觉外部参数标定及内外参数评价

王子昂， 李 刚， 刘秉琦， 黄富瑜， 陈一超

陆军工程大学石家庄校区电子与光学工程系， 河北 石家庄 050003

引 言

在红外光谱谱段， 短波、 中波、 长波主要的大气窗口分别为0.7～2.5， 3～5和8～14 μm[1]。 由于不同物质对于可见光、 红外线吸收性能不同， 因此通过红外相机可以探测可见光无法看到的一些差别。 长波红外一般用于探测300 k左右的目标， 即常温下目标。 与可见光相机相比， 双目超大视场长波红外相机具有不受光照强度影响， 在复杂条件下全天候工作， 获取大空域信息等诸多优点[2-3]。 军事应用中， 需要红外立体视觉系统对目标进行定位以获取完整的空间信息， 为作战决策奠定基础； 民用领域中， 将红外立体视觉系统装载到车辆上， 可在车辆行驶过程中规避障碍物， 提高车辆驾驶安全性。 伴随智能化的快速发展， 立体视觉在视觉测量[4]， 二维运动图像的三维重建[5]， 即时定位与地图构建[6]等方面起着关键作用。 立体视觉旨在从双目相机拍摄图像中获取密集的3D信息， 图像三维重建精度主要取决于相机系统参数， 标定的过程就是解算相机系统参数的过程。 内部参数是相机的固有属性， 它表示相机系统的物像关系。 外部参数标定指求解两个相机之间的坐标变换矩阵， 该矩阵描述右目相机相对于左目相机的位置关系。

目前， 外部参数标定方法主要分为两类： 需要移动相机的外部参数标定[7]和固定相机的外部参数标定[8]。 在前者中， 手眼标定和基于反射镜的方法最常用； 对于后者， 研究人员移动相机视野中的物体来计算姿势并重建轨迹。 针对不同立体视觉系统和应用， 标定模型的相机参数和计算方法各不相同。 此外， 自标定方法和其他新兴方法由于准确性不高或者实现复杂， 不能用于超大视场长波红外立体视觉系统。 由于超大视场长波红外图像低分辨率和严重失真， 导致标定准确性下降， 常见的外部参数标定方法[9-11]不再适用。 此外， 针对标定精度的评价方法也有待提高。 对于内部参数标定的评价， 角点平均重投影误差(mean reprojection error， MRE)运用最普遍； 针对内外参数的整体评价， 大多数方法从三维重建入手， 对角点进行三维重建， 根据角点间相对距离评价标定精度[12]； 或者运用MRE评价内部参数后， 直接以高精度坐标测量机测得的外部参数作为真值评估外部参数标定[13]。 前者依赖于三维重建方法的准确性， 在评价过程中不可避免掺杂了三维重建方法的本身误差； 后者需要高精度的三维坐标测量仪器， 对实验设备要求很高。

为标定超大视场长波红外立体视觉外部参数并易于评价参数标定准确性， 在Scaramuzza相机模型[14]标定单目相机基础上， 提出了一种基于最小二乘法的外部参数标定方法； 根据单目相机内部参数的角点平均重投影误差评价方法， 提出一种双目平均重投影误差(binocular mean reprojection error， BMRE)的内外参数评价方法。 该方法提高了外部参数标定精度， 并且简化了内外参数评价过程。

1 标定方法

1.1 超大视场相机模型

由于超大视场长波红外相机成像过程不符合传统小视场成像的线性模型， 而是遵循非相似成像原理， 所以通用的Scaramuzza相机模型在超大视场长波红外相机标定过程中被使用。 在该相机模型中， 传感器平面像点p(x,y)与图像平面像点q(u,v)之间关系表示为

(1)

其中，c，d和e为常数， 表示镜头光轴和传感器平面中心非对准的误差系数， (u0,v0)为图像畸变中心坐标。 标定板上角点Pw与p之间关系表示为

(2)

f(ρ)=k0+k2ρ2+…+knρn

(3)

(4)

其中，λij为正常数， 表示第i幅图像中第j个角点成像的比例系数；k0,k2， …，kn是泰勒多项式系数， 通常n=4； [r1r2t]i表示第i幅图像中标定板与相机的相对位置关系，r1和r2为旋转向量，t为平移向量。

1.2 基于最小二乘法的外部参数标定

Scaramuzza相机模型描述了单目相机成像中的物像关系， 然而， 因为该相机模型不能标定双目相机的外部参数， 所以无法进行立体视觉标定。 本节在该相机模型基础上， 提出一种最小二乘法方法来标定立体视觉中的外部参数。

角点在世界坐标系中与相机坐标系中的关系可由式(5)和式(6)表示

(5)

(6)

其中，Plij和Prij分别代表世界坐标系中第i幅图像的第j个角点在左目相机坐标系和右目相机坐标系中的投影坐标， [r1r1t]li， [r1r1t]ri， [XwXw1]T从单目相机模型的标定结果中获得。

根据三维空间中两个坐标系转换关系

Prij=RPlij+t

(7)

其中， 旋转矩阵R和平移向量t共同描述了右目相机相对于左目相机的位置， 将Plij和Prij展开为坐标形式可以得到

(8)

将R和t展开为坐标形式， 并把式(8)转化为线性方程组形式

(9)

将所有Plij和Prij代入式(9)即得到以R和t为未知量的超定线性方程组， 运用最小二乘法求出该超定线性方程的最优解

(10)

最终， 外部参数R和t为

(11)

t=[t1t2t3]T=[txtytz]T

(12)

1.3 基于双目角点重投影的内外参数评价

双目内外参数的标定直接影响立体视觉图像匹配和目标定位， 目前存在两种常用方法对内外参数准确性进行评估， 一种是采用三维重建后目标点间距与实际间距的差值来评价外部参数标定准确性； 另一种是以高精度坐标测量机对外部参数的测量结果为真值， 根据外部参数真值与标定值的差值评价标定准确性， 坐标测量机测量精度要达到微米量级， 这种方法对实验设备要求很高。 在评价单目相机内部参数标定准确性时， 通常用到角点平均重投影误差MRE， MRE表示三维空间中角点经过已标定相机模型成像后的投影点与图像检测角点的接近程度。 为简化内外参数评价， 避免引入其他变量， 本节在内部参数评价方法基础上提出一种双目角点重投影误差的内外参数评价方法。

单目相机内部参数评价的角点重投影过程如图1。

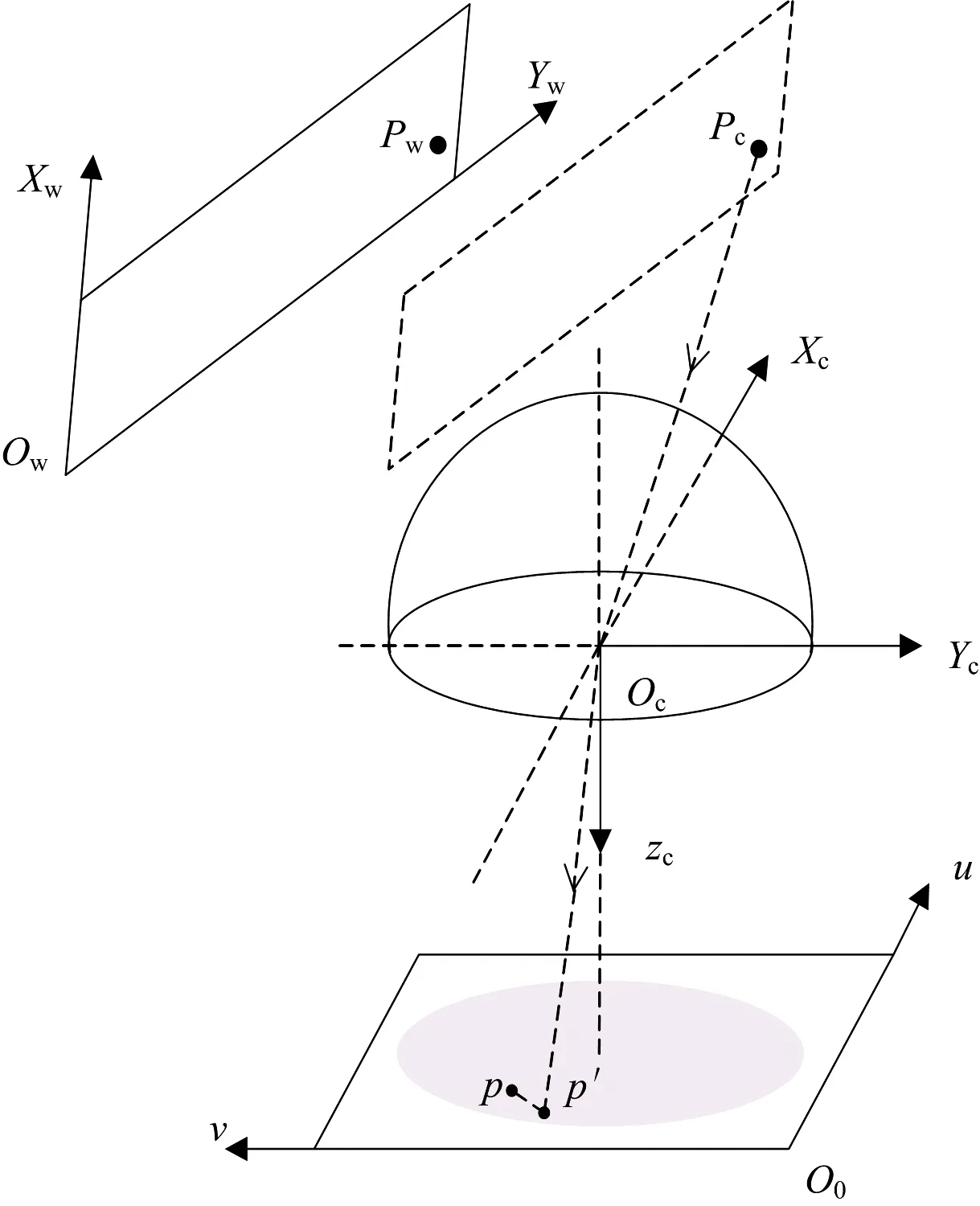
图1 单目相机角点重投影过程

在标定出单目相机成像模型后， 根据第i幅图像中标定板相对于相机的外部参数， 将标定板上角点Pw投影到相机坐标系为Pc

Pc=[r1r2t]iPw(13)

Pw和Pc实际是同一个点， 只是在世界坐标系和相机坐标系中该点坐标不同。 展开式(13)， 可以得到

(14)

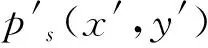
(15)

根据Scaramuzza相机模型可以得到

(16)

p′=(u′，v′)

(17)

p′与p的欧式距离即该角点的重投影误差， 一次标定实验中所有角点重投影误差的均值即MRE。 根据单目相机内部参数角点重投影误差评价方法， 引入立体视觉标定结果中的外部参数， 提出一种双目角点重投影误差的内外参数评价方法， 如图2。

在分别标定出左右目相机成像模型后， 根据第i幅图像中标定板相对于左相机的外部参数， 将标定板上角点Pw投影到左相机坐标系为Pl

Pl=[r1r2t]liPw

(18)

根据标定结果中表征左右目相机相对位置关系的外部参数， 通过式(19)将Pl投影到右相机坐标系中， 得到Pr

Pr=RPl+t

(19)

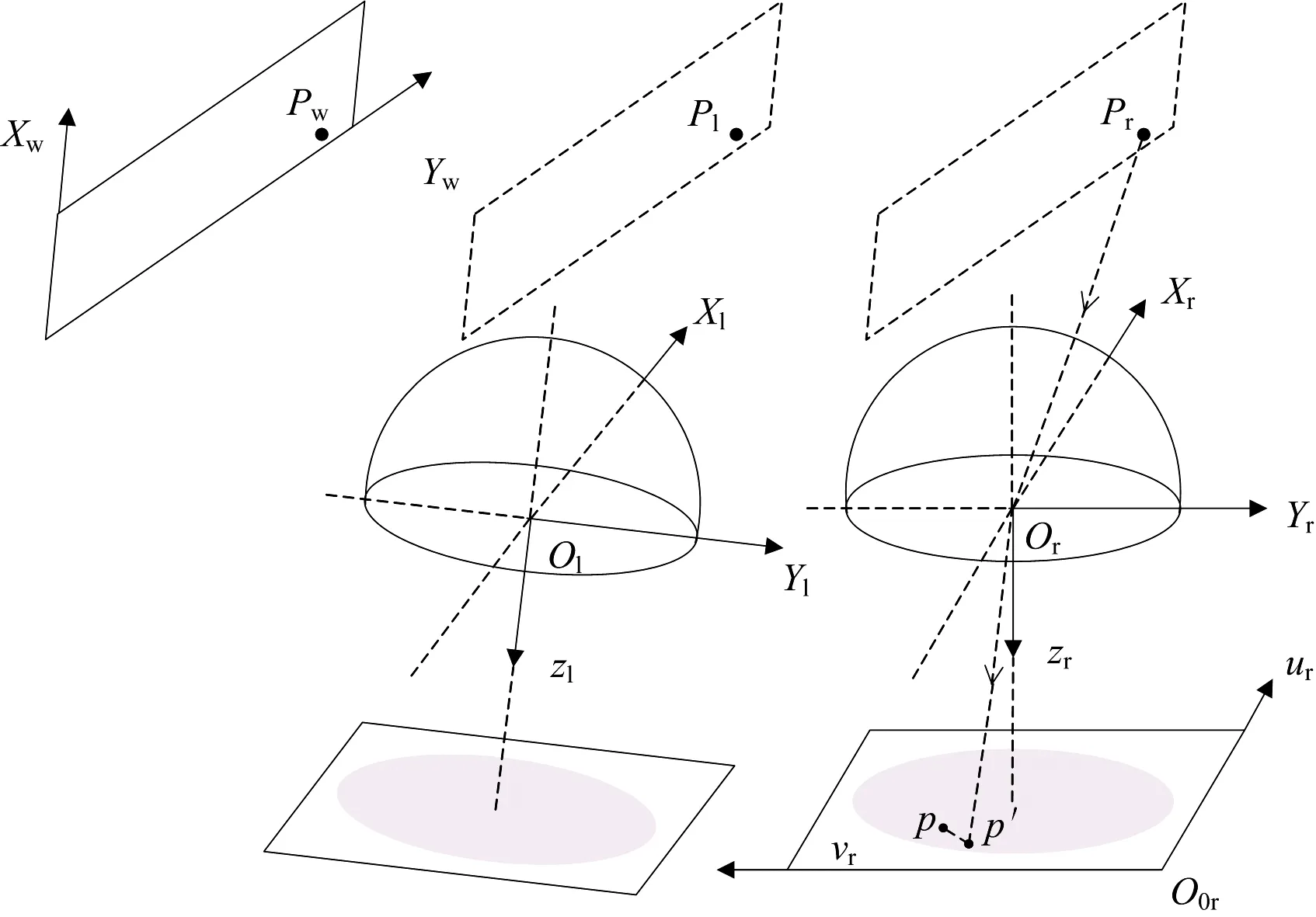
图2 双目相机角点重投影过程

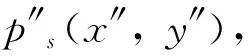
(20)

(21)

p″=(u″，v″)

(22)

P″与p的欧式距离即该角点的双目重投影误差， 单目相机角点重投影误差取决于单目相机标定的准确性， 而双目重投影误差不仅与单目相机标定参数有关， 而且受到双目标定外部参数的影响， 因此双目相机角点重投影误差应该大于单目相机角点重投影误差。

2 实验部分

超大视场红外立体视觉实验系统如图3， 整个装置由主动红外辐射自适应标定板、 双目超大视场长波红外相机、 计算机组成。 标定板根据帕尔贴原理制成， 通电后黑色标定块发热， 白色标定块制冷， 从而在标定块连接处产生明显的角点， 这些角点作为标定过程的目标点进行相机标定。 标定板采用模块式设计以便根据实验需求调整角点数量， 本实验中采用图中红色矩形框内部标定块。 通过设置标定板中的电流大小， 可对标定块温度进行控制， 从而实现对相机像面探测器响应波段的自适应。 图4显示了超大视场长波红外相机(FOV=210°)拍摄的标定板图像。 立体视觉系统中的超大视场长波红外相机安装在平行导轨上， 在导轨上平移镜头改变左右目相机相对位置， 调整镜头下方调节机构改变左右目相机的旋转角度， 从而改变双目相机之间的外部参数。 通过相机与计算机的连接， 计算机屏幕能实时显示并储存图像。

图3 实验系统

3 结果与讨论

实验过程中， 通过调节相机镜头使标定板位于图像中不同位置并且具备不同姿态， 从一系列图像中选取16幅作为标定的输入图像。 由于超大视场红外图像高噪声、 低分辨率、 低对比度特性， Bouguet[15]角点定位方法准确性不高，实验中采用基于多项式曲线拟合方法定位角点。 该方法主要包括图像边缘检测、 角点初步定位、 边缘曲线多项式拟合、 求解两拟合曲线交点。 为充分验证基于最小二乘法的外部参数标定方法一般性， 实验过程中使用FOV=180°和FOV=210°的两组镜头分别进行3组标定实验， 并且与Bouguet外部参数标定方法进行比较， 实验结果如表1。

图4 超大视场红外标定板图像

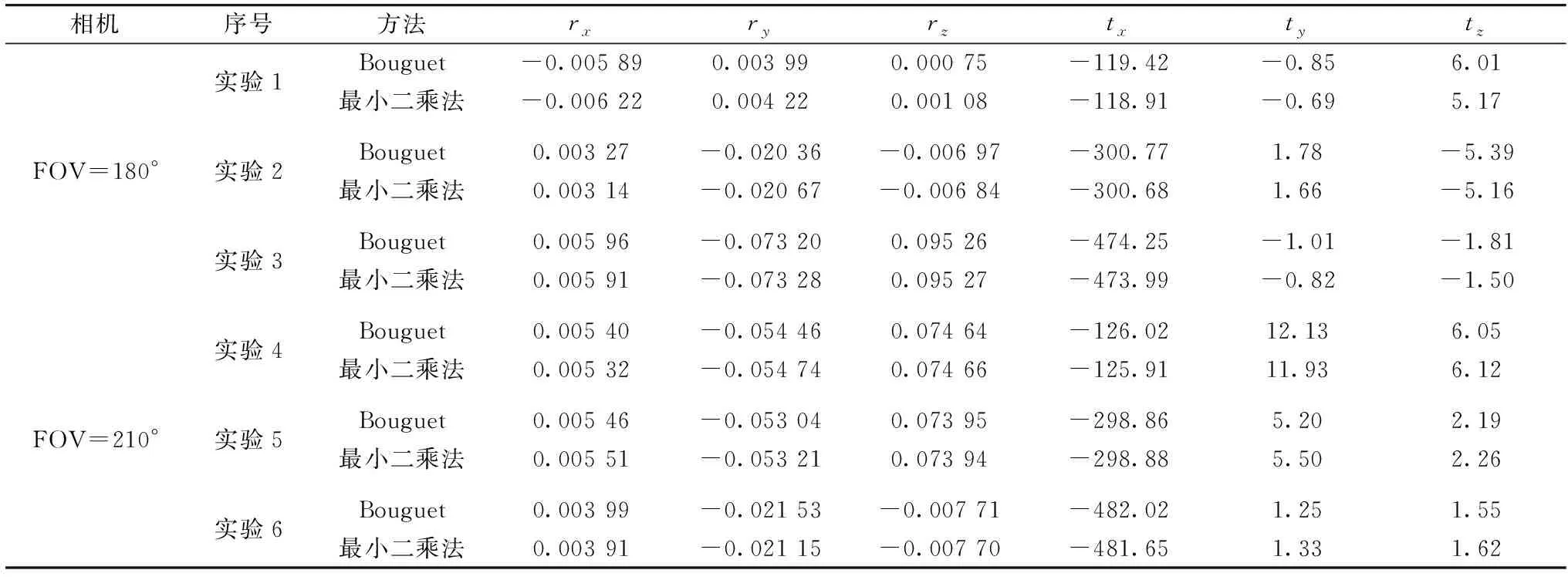
表1 外部参数标定结果

表1中rx，ry和rz根据罗德里格斯转换从旋转矩阵R得到， 它们分别表示右目相机相对于左目相机在x，y和z三个方向上的旋转角度。 从表1可以看出， 两种方法标定的外部参数相近， 直观上无法比较外部参数标定准确性。 因此， 运用基于双目角点重投影方法对外部参数准确性进行评估， 两种标定结果的双目角点平均重投影误差如表2, 折线图如图5。

从表2可以看出， Bouguet方法BMRE在0.782～0.943之间， 而基于最小二乘法方法BMRE在0.620～0.754 pixels之间， 并且每组实验中基于最小二乘法方法BMRE都明显小于Bouguet方法BMRE， 这表明基于最小二乘法方法比Bouguet方法标定结果更准确。 从图5可以发现， 同一折线中后三组实验BMRE明显大于前三组实验， 这表明POV越大的红外相机， 成像畸变越严重， 标定后BMRE越大； 由于表1中ty和tz远小于tx， 所以tx大致体现左右目相机之间的基线距离。 在标定同一双目相机时， 伴随基线距离的增加， BMRE有增大趋势， 这说明标定参数准确性伴随基线距离增加而降低。 为比较BMRE和MRE的差别， 实验中选取了右目相机MRE和双目相机基于最小二乘法方法BMRE， 如图6。

理想情况下， 所有角点成像关系都应该完全符合成像模型， 因此MRE=0， BMRE=0。 但在实际情况中为标定更多角点减小误差， 避免某个角点占标定模型权重过大， 角点数量要远多于标定过程中方程组未知量数量， 标定出的相机成像模型是方程组的最优解， 所以角点成像关系并不完全符合成像模型， MRE>0， BMRE>0。 MRE和BMRE越小表明标定结果越准确。 从图6可以发现， 单目相机MRE在0.31～0.36之间， 明显小于BMRE。 这是因为右目MRE只表征了右目镜头标定误差， 而BMRE不仅包含右目镜头MRE， 而且增加了双目相机之间外部参数的标定误差， 所以BMRE>MRE。 这也符合1.3节中基于双目角点重投影标定参数准确性评价对于右目角点重投影过程的分析。

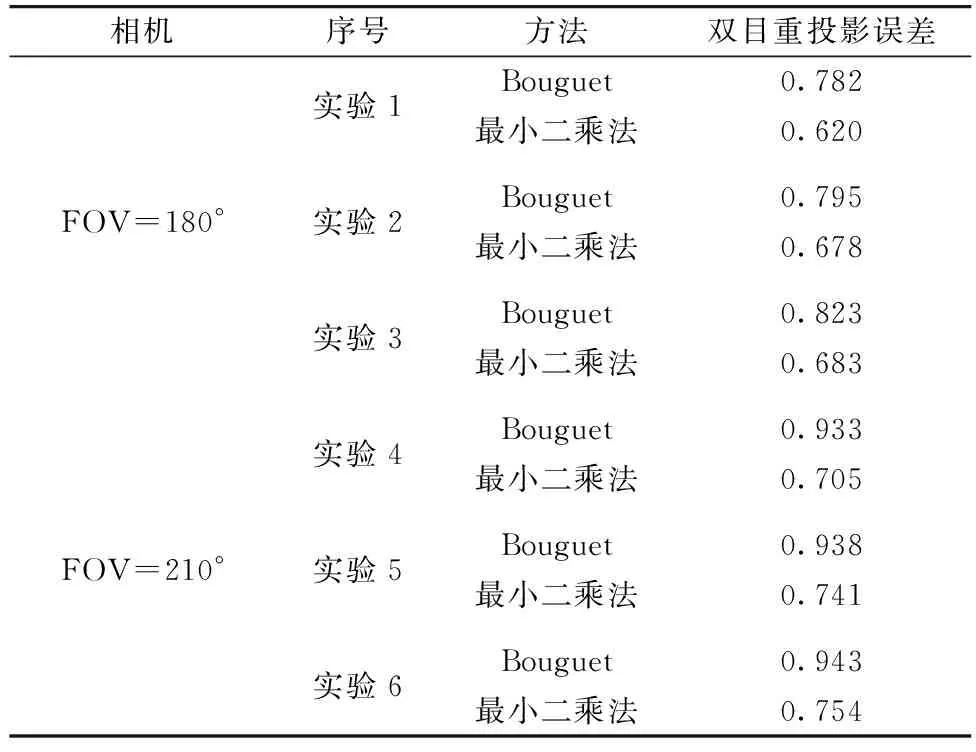
表2 双目平均重投影误差

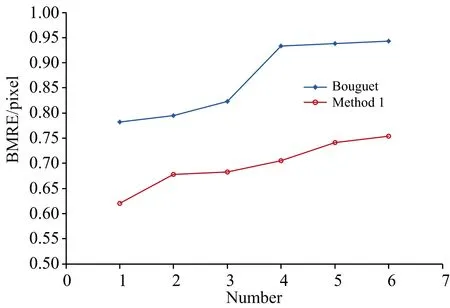
图5 双目平均重投影误差折线图

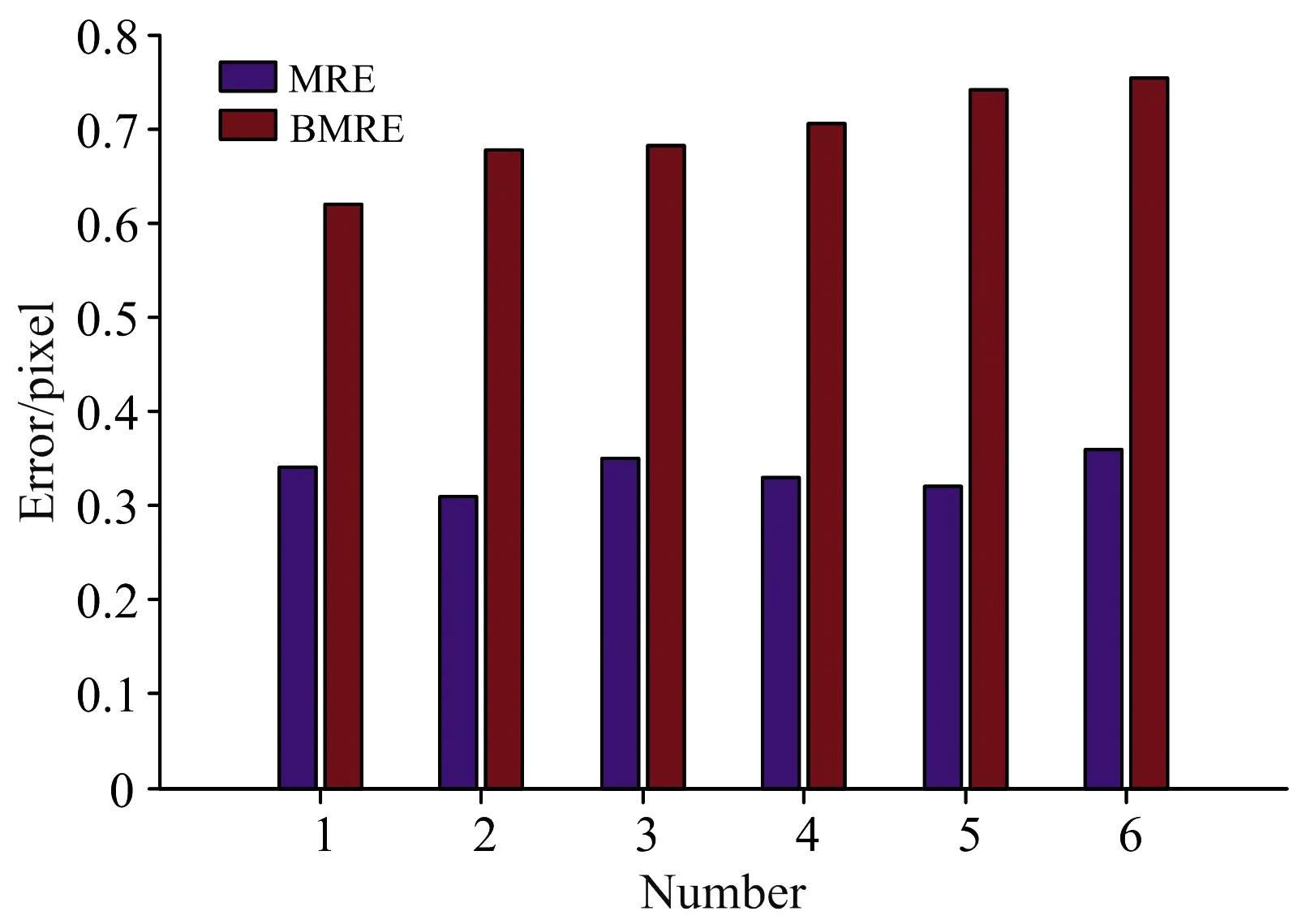
图6 单目平均重投影误差与双目平均重投影误差折线图

4 结论

为标定超大视场长波红外立体视觉外部参数， 提出一种基于最小二乘法的外部参数标定方法， 为量化内外参数标定准确性， 提出一种双目角点重投影误差的评价方法。 实验表明： 基于最小二乘法的外部参数标定方法能准确标定超大视场长波红外立体视觉外部参数， 并且双目角点重投影误差可以精确评估内外参数标定精度。 与广泛使用的bouguet方法相比， 外部参数标定更精确； 相比于三维重建计算角点间距的评价方法， 本文方法不引入角点三维重建的额外误差； 相比于运用微米级坐标测量仪器的评价方法， 本方法操作简便， 避免了对实验设备的高要求。 本文方法提高了外部参数标定准确性， 简化了外部参数评价过程， 将促进超大视场长波红外相机在计算机视觉领域的应用， 拓展了红外光谱中长波波段相机的使用。