集装箱舱口盖箱脚安装精度控制分析
2020-09-05陈建春
陈建春
(南通中远重工有限公司, 江苏 南通 226116)
0 引言
舱口盖是船舶的重要设备之一,肩负着密封舱口、保护货物和支撑平台等作用[1-2]。装载标准集装箱的舱口盖通常在总装阶段就将箱脚按照标准间距装焊到顶板上。为保证集装箱能够顺利堆放并受力良好,箱脚装焊后需要满足一定的尺寸精度要求。因此,制造过程中如何对箱脚位置进行快速测量,并降低现场施工人员对测量数据的处理难度,提高数据判定的可靠性,从而减少集装箱箱试比例、降低制造成本,有着极其重要的工程意义。本文以某套集装箱舱口盖为研究对象,利用全站仪测量箱脚三维坐标,并结合Matlab编程计算来判定箱脚安装精度是否符合要求的可行性,为集装箱舱口盖箱脚的现场施工尺寸的测量与控制提供指导。
1 箱脚安装技术要求
麦基嘉设计规范中对舱口盖箱脚的安装尺寸有如下要求:
(1)箱脚间距:以常见的6.096 m(20 ft,下文简称为20′)和12.192 m(40 ft,下文简称为40′)标准集装箱为例。其箱脚要求见表1,示意见图1(a)。

表1 箱脚尺寸装焊要求 单位:mm
(2)箱脚水平公差:对一组中的任意三个箱脚构成一个平面,第四个箱脚到该平面的距离H不超过4 mm,示意见图1(b)。
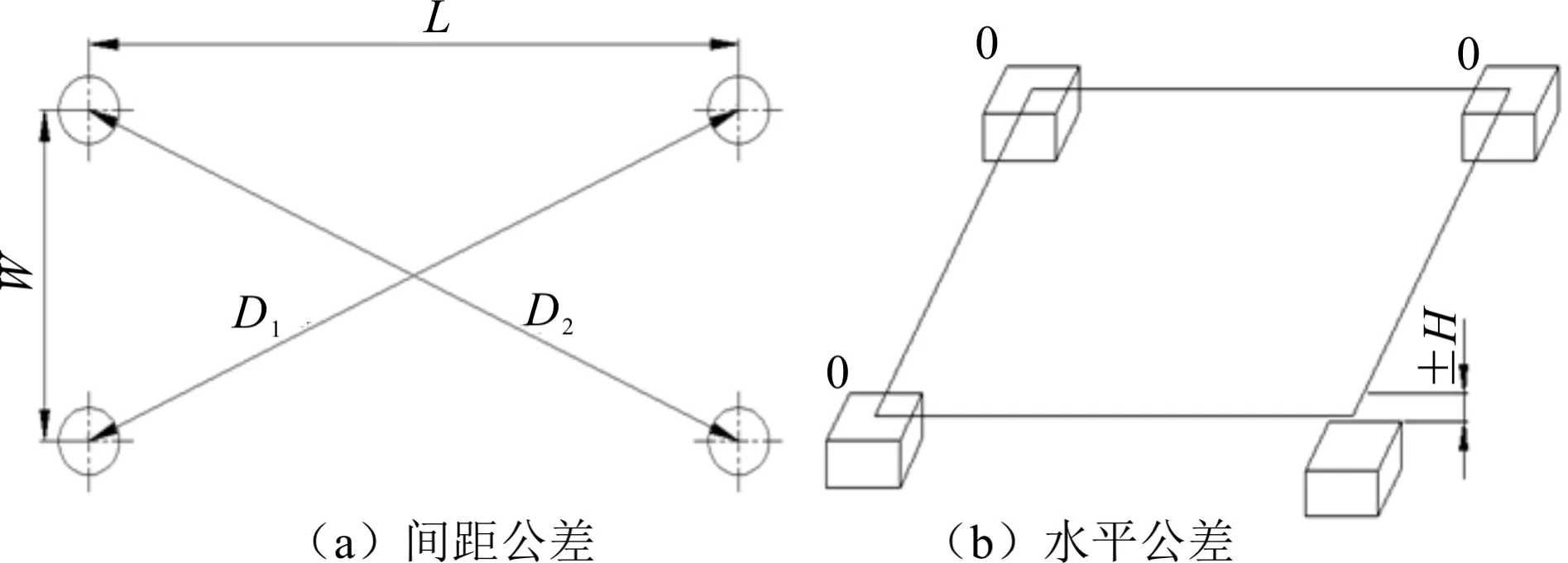
图1 箱脚装焊技术要求示意图
2 箱脚三维坐标测量
目前各舱口盖制造厂家对箱脚尺寸的测量通常采用以下方式:通过钢卷尺对箱脚构成的四边形的边长和对角线长度进行测量,与技术要求对比判定是否超差;通过水准仪和标尺对箱脚高度进行测量,再通过复杂的数学运算判定是否超差,这对现场施工人员来说具有较大的难度。
配合水平高度标尺,全站仪可以一次性测量各箱脚的三维坐标,这样既提高了测量效率,又减小了传统测量方法因基准多次变换造成的测量误差。测量示意图见图2。将测量数据通过Matlab程序实现自动计算,可以快速判定箱脚装焊尺寸是否满足技术要求,具有重要的工程应用价值。

图2 箱脚尺寸测量示意图
3 箱脚尺寸Matlab计算程序
3.1 箱脚间距计算
如图2所示,设定4个箱脚的坐标分别为A(x1,y1,z1)、B(x2,y2,z2)、C(x3,y3,z3)、D(x4,y4,z4)。箱脚A到箱脚B的间距W1可表示为:
(1)
同理可求得其他箱脚间距W2、L1、L2、D1和D2。
3.2 箱脚水平公差计算


(2)
则平面ABC方程可表示为:
P(x-x1)+Q(y-y1)+R(z-z1)=0
(3)
令S=-Px1-Qy1-Rz1,可得平面ABC方程为:
Px+Qy+Rz+S=0
(4)
因而D到平面ABC的距离HD为:
(5)
同理,可分别计算得到A到BCD平面的距离HA,B到ACD平面的距离HB,C到ABD平面的距离HC,将其中的最大值作为箱脚水平公差的判断依据。如果不超过许可范围,则表明该组4个箱脚水平满足要求;如果超出许可范围,可根据计算结果找出所对应的箱脚,以便更有针对性地对箱脚高度进行相应的调整。
将测得的箱脚三维坐标值分别记录在Excel表中,利用Matlab中的“xlsread”函数直接读取所需的数据。
Matlab实现计算的程序如下:
%读取箱脚A、B、C、D的三个坐标数据
A=xlsread(′箱脚坐标测量数据.xlsx′,′A2:C2′);
%这里的A2、C2为Excel表中第二行的A列、C列,下同
B=xlsread(′箱脚坐标测量数据.xlsx′,′A3:C3′);
C=xlsread(′箱脚坐标测量数据.xlsx′,′A4:C4′);
D=xlsread(′箱脚坐标测量数据.xlsx′,′A5:C5′);
%分别提取箱脚x、y、z坐标数据
x1=A(1,1);
y1=A(1,2);
z1=A(1,3);
…
%计算箱脚间距
W1=sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2);
W2=sqrt((x4-x3)^2+(y4-y4)^2+(z4-z3)^2);
…
%ABC三点构成的平面方程
syms x y z s p q r
E1=[ones(4,1),[[x,y,z];A;B;C]];
detd=det(E1);
disp(strcat(′平面方程为:′,char(detd),′=0′));
%计算D到ABC平面的距离
N=coeffs(detd);
s=N(1,1)′;
p=N(1,2)′;
q=N(1,3)′;
r=N(1,4)′;
HD=abs(p*(x4-x1)+q*(y4-y1) +r*(z4-z1) +s)/sqrt(p^2+q^2+r^2);
disp(strcat(′点到平面的距离HD为:′,char(HD)))
…
%确定到任意三个箱脚构成平面的最大距离
H0=[HD, HA, HB, HC];
HM=max(H0)
%判定箱脚尺寸是否超差(以20′集装箱为例)
syms b1 b2 b3 b4 b5
b1= abs(B1-2259);
b2= abs(B1-2259);
b3= abs(L1-5853);
b4= abs(L2-5853);
b5= abs(D1-D2);
if b1>2 | b2>2 | b3>4 | b4>4 | b5>5 | HM>4
disp(′箱脚尺寸超差′)
else
disp(′箱脚尺寸符合要求′)
end
4 实例计算与分析
某舷侧舱口盖顶板箱脚布置见图3。图中,中间区域虚线连接处表示集装箱堆放位置,分别命名为20′-1(20′集装箱1号堆放位置,下同)、20′-2和40′-1。

图3 舱口盖顶板箱脚布置图
为便于描述,分别以20′-1和40′-1的四个箱脚为研究对象。20′-1四个箱角分别为A、B、C、D;40′-1四个箱角分别为A、B、E、F,并将A点作为坐标原点,测得其他箱脚坐标B(2 260,1,1)、C(2 259,5 851,12)、D(1,5 851,8)、E(2 260,11 985,2)、F(-1,11 986,0)。箱脚间距计算结果见表2,箱脚水平计算结果见表3。
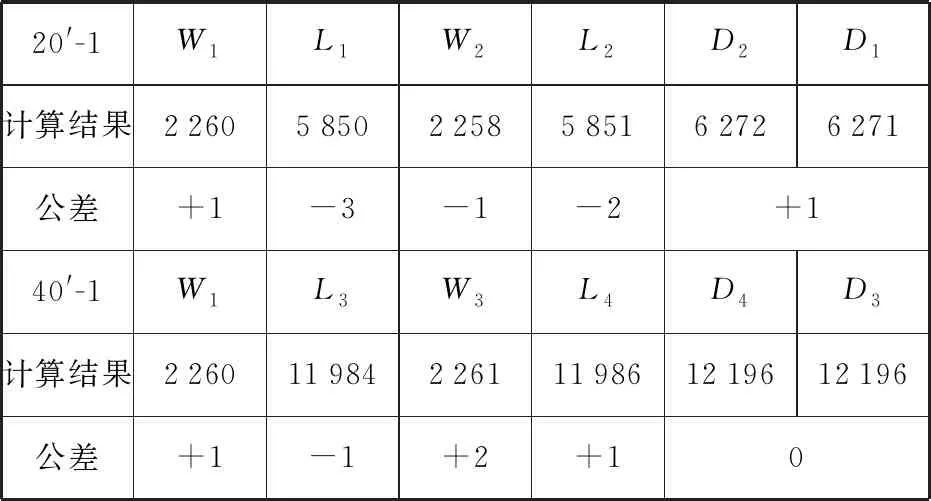
表2 箱脚间距计算结果 单位:mm

表3 箱脚水平计算结果 单位:mm
由表2、表3可知,Matlab计算程序可以根据测得的箱脚三维坐标快速计算出相关尺寸公差,计算结果表明这两组箱脚安装符合制造要求。同时,一组箱脚中任意一个到另三个构成平面的距离H基本相等,因此根据实际制造的精度要求,可以只计算其中任意一个箱脚到平面的距离,并将此作为判定箱脚水平是否超差的依据。
为了验证计算结果的准确性,还利用模拟集装箱的工装对箱脚进行了套放试验。试验结果显示,试验结果与计算判定结果一致。箱脚安装除了保证本区域内各个尺寸公差满足技术要求外,还要考虑相邻区域集装箱堆放过程不能相互干涉。图3中,为了不让20′-1和相邻的20′-2堆放集装箱后最上层出现“挤死”现象[3],还需要控制箱脚A、D与B、C水平高低差值h(假定A、D连线平行于B、C连线,与水平面成β夹角,见图4。图中:d为两集装箱堆放后外侧面间距,T为集装箱上表面到箱脚表面的总高度。
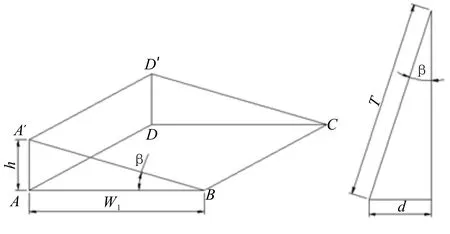
图4 箱脚水平高低差
根据设计要求,两集装箱堆放后外侧面间距d=38 mm。假定堆放6层集装箱后顶层集装箱上表面到箱脚表面的总高度T=16 221 mm,箱脚A到B理论间距W1=2 259 mm,容易求得:
(6)
由此可知,箱脚水平高低差的许可范围与集装箱设计的堆放层数和间距有关(忽略舱口盖顶板变形等因素)。当集装箱堆放高度增加或者设计的堆放间距减小,箱脚水平高低差许可值将进一步减小。因而即使箱脚在同一水平面内,其高低差也需要控制在一定范围以内,才能保证集装箱堆放时不会因倾斜造成顶层“挤死”或堆放干涉问题。
5 结论
本文通过全站仪对集装箱舱口盖顶板安装的箱脚三维坐标进行测量,利用Matlab编程实现了对箱脚装焊位置尺寸的计算,利用实例验证了方案的可行性,并得出了以下结论:
(1)该测量计算方式具有很好的现场适用性(效率高、难度低),计算结果可靠,可减少箱试比例、降低制造成本。
(2)一组箱脚中任意一个到另三个组成平面的距离基本相等,按照舱口盖箱脚制造精度可以只计算其中任意一个箱脚到平面的距离,并据此判定平面水平是否超差。
(3)受集装箱堆放的设计高度和间距限制,箱脚水平高度差还需考虑与相邻堆放区域的相互影响,以免因水平高低倾斜造成顶层“挤死”或堆放干涉问题。
