基于剩余寿命预测的维修与备件订购联合策略优化
2020-09-04张新辉王雷震
张新辉,王雷震,赵 斐,3
(1.东北大学 秦皇岛分校,河北 秦皇岛 066004;2.东北大学 信息科学与工程学院,辽宁 沈阳 110819;3.中国人民解放军陆军工程大学(石家庄校区) 装备指挥与管理系,河北 石家庄 050003)
设备故障会中断正常生产运行,不仅会导致巨大经济损失,而且某些设备故障还会造成人员伤亡、环境污染等灾难性事故,提高设备可靠性、降低发生故障概率尤为关键,所以维修是主要手段。工业企业中常采用基于时间的维修策略和基于状态的维修策略[1-5]。前者是指每隔固定时间对设备进行维修,如役龄更换策略[4];后者是依据设备健康状态的实时信息做出决策[6]。维修产生备件需求,而备件库存状态会制约维修活动的顺利开展。所以,何时订购备件满足维修需求,同时降低备件管理成本是决策者关心的问题。已有学者针对单部件系统提出了基于状态的预防性维修和备件订购的联合优化[7-8]。
随着传感器技术的发展,利用实时的设备健康状态信息,预测剩余使用寿命进而将其用于设备健康管理决策,成为故障预测与健康管理的核心内容[9-12]。已有学者基于RUL(remaining useful life)展开对维修与备件订购决策的联合优化。Wang等[13]所提出的序贯联合优化策略模型首先确定最佳的设备更换时间,进而优化订货点。基于此研究,蒋云鹏等[14]同时优化设备更换时间和备件订购时间,并与序贯联合策略优化结果比较,最终表明联合决策更有效。但是,他们均未考虑订购备件的相关费用[13-14]。Wang等[15]针对不可修系统提出了备件订购与更换联合策略,该策略下在任一监测时刻利用历史状态信息预测剩余寿命,并结合订购点、预防性更换时刻以及下次监测时刻可能出现的各种情形,构建最小化单位时间内期望成本的目标函数,同时优化订购点和预防性更换时刻。以上研究虽考虑了设备剩余使用寿命,但主要用于维修决策中,备件订购决策基于退化水平或设备更换时刻。然而,决策者会通过比较设备剩余使用寿命长度与备件提前期的长度判断是否订货。
因此,本文针对单部件系统在预测RUL的基础上提出联合优化维修与备件订购的策略。针对此策略,通过分析所有可能更新事件,利用更新报酬理论建立联合策略优化模型,设计离散事件仿真算法进行优化。最后,通过实例验证联合策略模型和算法的有效性。
1 基于剩余使用寿命的维修与备件订购联合策略问题描述
考虑系统从新状态投入使用开始发生退化,每隔T周期监测系统以获取健康状态信息。传感器设置采集信息的T有所不同,可以是1 h、1 min或10 s。由于获取到的状态信息是连续的,所以视为实时监测。系统退化过程服从Wiener过程,根据控制限策略利用监测时刻系统的退化水平决定维修活动[13,16],即当退化量达到预防性更换阈值Lp,则进行预防性更换;若超过故障阈值Lc,则进行故障更换。当更换系统时需要考虑备件的可获取性,即未订购、已订购未到货、已到货。通常,当备件还未订购时采取紧急订货方式对系统进行预防性或故障更换;若虽已订货但未到,则延迟更换直至备件到货。紧急订购的备件费用要比正常订购的备件费用高,且提前期较短,可忽略。
利用监测得到的健康状态信息,预测RUL并判断是否在该监测点订购备件。在此,引入订货阈值q,即剩余使用寿命与提前期之间差值的上限。若在时刻tk,设备剩余寿命lk与备件提前期L(L=mT)之差满足条件lk−L≤q,则订购备件,订购点t0=tk且备件经时间L到货;否则,不订购直至下次监测时刻再判断。如图1所示,若在tk时刻对设备状态进行监测,预测其剩余使用寿命为lk,显然若订购阈值为q1时,lk−L<q1,则在t1时刻订购备件且经提前期L后到货,即备件在tk+3时刻到货进入存储状态;若订购阈值为q2时,由于lk−L>q2,那么在时刻tk不订购备件。在此联合策略中,订货阈值q反映了剩余使用寿命与提前期之间的关系,即当剩余使用寿命较长而提前期较短时,则暂时不订货;否则,订购备件。但是,订货阈值q的设置需要通过联合策略模型确定,为此将其作为决策变量。
2 联合策略优化建模与离散事件仿真算法设计
2.1 维纳过程的剩余使用寿命预测
每隔周期T采集系统状态信息,得到任一监测时刻tk(tk=kT)的退化量X(tk),{X(tk),tk>0}服从维纳过程

其中, µ为漂移参数; σ为扩散参数;B(t)为标准布朗运动(B(tk)∼N(0,tk))。时刻tk到时刻tk+∆t的退化增量服从正态分布,即∆X=X(tk+∆t)−X(tk)∼N(µ∆t,σ2∆t)。在初始时刻,系统退化量为0,即X(0)=0。

图 1 维修决策与备件订购联合优化示意图Figure 1 Joint optimization diagram of maintenance decision and spare ordering
如果系统运行到时刻tk还未失效,则

其中,xk是tk时刻的退化量。由布朗运动性质和Wiener过程定义可知,式(2)依然可以看作带线性漂移的布朗运动,其初始时刻为tk,初值为xk,则系统在tk时刻的剩余使用寿命Lk为

剩余使用寿命Lk服从逆高斯分布,其概率密度函数和分布函数分别为

剩余使用寿命Lk的期望和方差为

2.2 基于RUL的维修与备件订购联合策略优化建模
每次以成本Ci对系统进行状态监测。若Lp≤X(tk)≤Lc,则以成本CR进行预防性更换;若X(tk)≥Lc,以成本CR进行故障更换,但还会导致损失CF。根据系统状态和备件状态综合分析进行联合决策,有6种更新事件(见表1)。其中,若需要更换系统时仍未订购备件,则紧急订购并立即更换(事件1和事件4);如图1中当订货阈值为q2时,tk时刻不订购备件但是系统可能在监测周期(tk,tk+1]内产生更换需求。当订货阈值为q1时,tk时刻订购备件,而系统可能在(tk,tk+2]内进行更换,而备件未到货,不得不等待备件到货更换,即事件2和事件5;另外,系统可能在备件到货后才需要更换,则立即更换,即事件3和事件6。通常,紧急订货的费用(Ceo)要高于正常订货的费用(Co),即Ceo>Co。若订购备件未到货,则会产生缺货成本;若备件到达未立即更换,则进入存储状态产生持有成本;其中,单位时间的缺货成本为Cs;单位时间的持有成本为Ch。
不可观测的退化过程{X(t);t≥0}是非递减的,可由可观测Markov 过程来描述[17],即Wiener最大过程

表 1 联合策略的所有可能更新事件Table 1 All possible renewal scenarios of the joint policy modeling



其中,订货时刻t0=jT。
基于各更新事件的期望成本和长度,采用更新报酬理论建立最小化单位时间内期望费用的目标函数(式(17)),得到最优的决策变量:订货阈值q∗和预防性更换阈值。

2.3 离散事件仿真算法设计
为了求解优化模型设计离散事件仿真算法(图2),步骤如下。
步骤1设置初始成本参数Ci、Co、Ceo、CR、CF、Cs、Ch,漂移系数µ、扩散参数 σ、L、T、Lc,最大计算次数Nmax,Lp=0。
步骤2设置预防性更换阈值Lp=Lp+1,q=0。
步骤3设置订货阈值q=q+1。
步骤4令总期望成本TC=0;总期望时长TL=0,运行次数i=0。
步骤5在Lp和q固定的情况下,运行次数i=i+1。
步骤6每隔周期T监测系统退化水平,依据式(2)得到退化量x并 进行累加,计算时刻t的累计退化量X(t);依据式(6)估计RUL,判断l(t)−L≤q,若满足,则判断t0≥0,即是否已经订货,若未订货则订购备件,否则转到步骤7。
步骤7判断当前检测时刻t的退化量,若X(t)≤Lp,则返回步骤5。若Lp≤X(t)≤Lc,则进行预防性更换;并进行如下决策:当t0=0,未订购备件,事件1发生;当t0≤t≤t0+L,备件已订购但未到货,事件2发生;当t0+L≤t,已到货,事件3发生。若X(t)≥Lc,则进行故障更换,类似地,根据备件各个状态可能发生事件4、事件5、事件6。

3 实例分析
为了验证模型的有效性,选取文献[18]中飞机发动机的案例展开研究。由于原始数据中航空公司每100次飞行循环检查一次,所以本文T=100。其中,通过采用极大似然估计得到发动机退化的维纳过程参数 µ=−0.014 78和 σ=0.399 97,即X(tk)=75+µtk+σB(tk),故障阈值Lc=0,成本参数如表2所示。
基于以上参数,采用MATLAB对离散事件仿真算法进行编程,得到最小的目标函数值为14.656 3,其中最优的订购阈值q∗=10T=1 000,预防性更换阈值L∗p=8。图3给出单位时间内的期望费用随订购阈值和预防性更换阈值变化的趋势,可以看出,当Lp固定时,单位时间内的期望费用随q增大呈现出先减小后增大的趋势。这是因为若q太小订购备件易导致系统故障时无可用备件,增加停工损失和缺货成本;但是q较大会增加备件的持有成本。同样,当q固 定时,单位时间内期望成本随Lp的增加先减小后增大,这是因为过大的Lp增加了预防性更换可能性且减少期望长度,导致单位时间内期望费用较高;Lp较小易导致故障发生,未能进行预防,使得单位时间内期望费用增加。图4给出了当订购阈值为最优值且Lp取不同值时,单位时间内的期望费用变化趋势,显然=8时目标函数取得最小值。

图 2 离散事件仿真算法Figure 2 Discrete-event simulation algorithm

表 2 成本参数Table 2 Cost parameters
文献[18]未对监测周期T进行优化,为此,本文分析了不同监测周期对最终决策的影响(见表3)。结果表明,当T逐渐增加时,最优的决策变量q∗和也随之增大,单位时间内的期望费用先降低而后不断增加。可以看出,当T=100时,单位时间内的期望费用不是最低的,而当T=300时,目标函数最低。显然为了节省成本,当前监测周期100应延长到300,即每隔300次飞行检查一次发动机。
表4给出了订货提前期对最优决策的影响,表明单位时间内的期望费用随L增大逐渐增大。这是因为系统退化过程不发生变化,由于L增大势必需要在剩余寿命较长的时候就开始订货,即q∗逐渐变大;而且一旦系统需要进行预防性更换或故障更换时,如备件已经订购但还未到,则增加了由于长时间等待备件导致的缺货损失,使得单位时间内的期望费用增加,所以L∗p减小,使得预防性维修时刻向到货点靠近。

图 3 单位时间内的期望费用随预防性更换阈值 Lp和订货阈值q 变化的趋势Figure 3 The expected cost per unit time in terms of the preventive replacement threshold Lp and the order threshold q
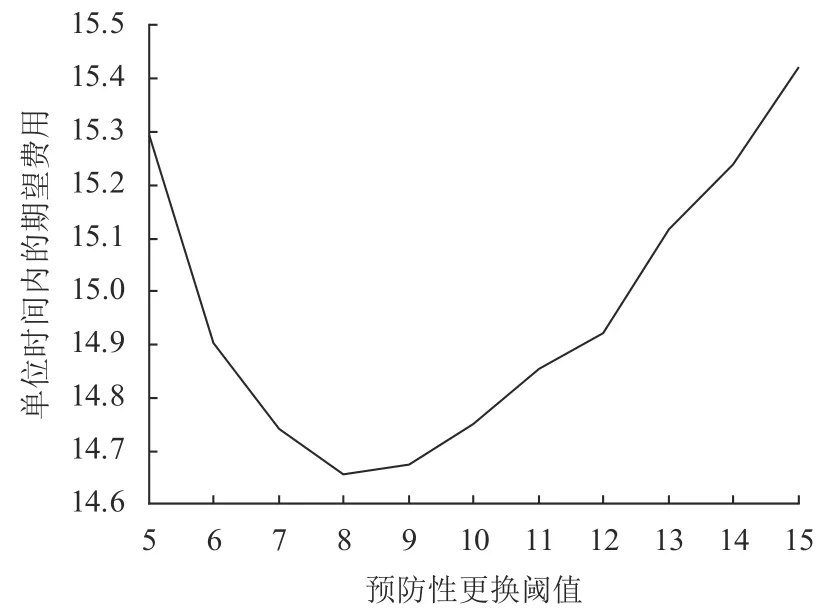
图 4 单位时间内的期望费用随 Lp变化的趋势(q=q∗)Figure 4 The expected cost per unit time under different Lp(q=q∗)
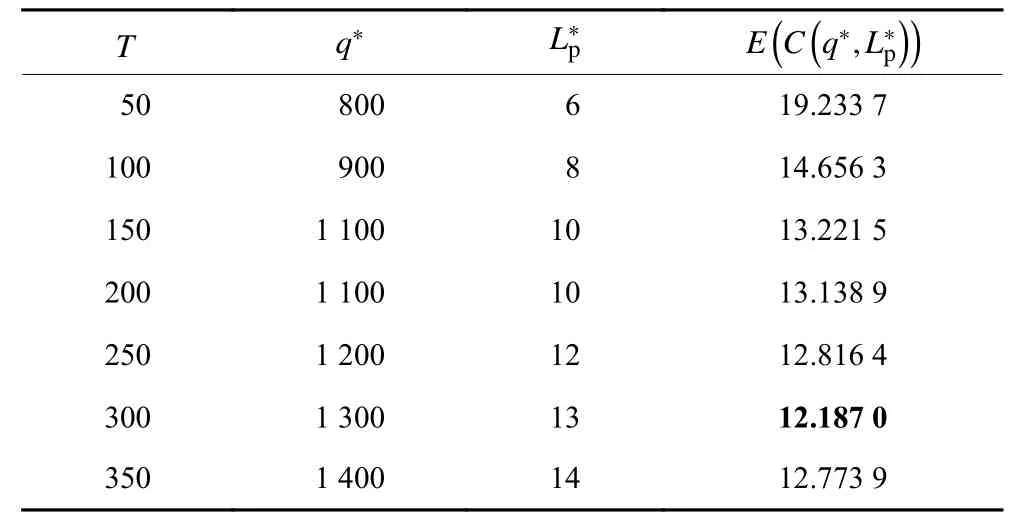
表 3 监测周期T对最优决策的影响Table 3 The influence of the monitoring interval Ton the optimal decisions

表 4 订货提前期 L对最优决策的影响Table 4 The influence of the order lead time Lon the optimal decisions
4 结论
针对单部件系统提出基于RUL的维修与备件订购联合策略,其中系统退化服从Wiener过程,维修策略采用控制限策略,在每个监测点确定系统退化量以确定进行预防性更换还是故障更换;同时,预测RUL并通过比较监测点剩余使用寿命与提前期之差与订货阈值的大小来确定是否订购备件,实现备件订购策略与系统实时健康状态的集成。构建了最小化单位时间内的期望费用模型并设计了离散事件仿真算法优化预防性更换阈值 Lp和订购阈值q。通过实例分析给出了最优解,并分析了监测周期和订货提前期对最优决策的影响。下一步研究将考虑对设备进行不完美维修。
