改进蚁群算法在移动机器人路径规划上的应用

陈 志，韩兴国

(桂林航天工业学院 机械工程学院，广西 桂林 541000)

0 引 言

传统的移动机器人路径规划算法主要包括人工势场法、网格法等[1,2]，但传统路径规划算法目标不可达性和局部最小点的问题容易导致路径规划的失败，且随着路径环境复杂性的增加，存在数据存储空间大、计算速度慢、实时决策差等缺陷[3,4]。

蚁群算法是由M.Dorigo等学者提出的分布式智能仿生算法[5]。该算法模拟了蚂蚁合作觅食行为的性质。它具有正反馈、高稳健性和并行性的优点，但是该算法存在搜索空间大、局部最优、搜索效率低、计算量大等问题[6,7]。张原艺等[8]提出一种改进的多步长蚁群算法。将蚁群每次迭代产生的最优路径作为引导径，利用路径引导搜索策略确定多步长的移动路径，提高搜索范围的多样性，该算法有效提高了算法跳出局部最优的能力，但改进算法在算法的收敛速度方面还有待改善。张强等[9]针对传统人工势场算法存在死锁及局部路径欠优等问题，对其进行改进。利用障碍物检测算法识别出有效障碍物和有效路径中间点，通过引力场和边界条件规划出起点到中间点的局部路径，将中间点置为新的起点进行反复迭代，直至起点与目标点重合则规划完成，解的质量明显提高，但仍存在寻优过程中搜索时间较长的问题。王慧等[10]利用粒子群算法个体加权平均值并加入惯性权重提出了一种改进粒子群路径优化算法，但该算法搜索到最优解时迭代次数较多，搜索时间较长。

鉴于此，提出了一种改进的蚁群算法。该算法根据中间节点与起始终端线之间的距离关系设置不均匀分布的初始信息素，减少了初始阶段的盲目性问题；将衰减因子引入启发函数，随着迭代次数的增加，启发式信息在路径选择中的作用逐渐减弱，从而加快了收敛速度；使用伪随机状态转移概率规则，并根据迭代次数和该迭代的最优解计算状态转移概率值，以自适应地调整确定选择和随机选择的比例。对于死锁问题，根据路径上丢失的蚂蚁数量，对不完整路径的最后两步进行处罚，以减少丢失蚂蚁的数量，确保算法的多样性。仿真实验在不同的移动环境中进行，实验结果表明，改进的蚁群算法在性能指标上有显著提高。

1 基本蚁群算法

蚁群算法模拟了蚂蚁“探索”的行为特征，即蚂蚁将使用前蚂蚁在觅食过程中留下的信息素，根据一定的概率选择路径或探索新的路径并同时分泌信息素。路径上的信息素会积累、挥发和扩散，并影响下面的蚂蚁。蚂蚁倾向于选择具有高信息素浓度的路径并最终寻找最佳路径[11]，蚁群算法的两个最重要的步骤就是路径选择和信息素更新。

假设蚂蚁k在t时刻位于节点i，则路径转换的概率可由式(1)表示，然后利用轮盘赌模型选择下一个节点

(1)

式中：C为蚂蚁允许在下一步选择的节点集；τij为路径(i，j)的信息素值；α为信息素激励因子，它反映了信息素浓度对路径选择的重要性，α越大则信息素对于路径选择越重要，蚂蚁将更倾向于选择大多数蚂蚁采取的路径；β是预期的启发因子，它反映了启发式信息在路径上的重要性。β越大则蚂蚁越倾向于选择最短路径；ηij(t)为启发式值，表示蚂蚁从节点j转移到目标节点g的期望程度，如式(2)所示

(2)

式中：djg是节点j和目标节点g之间的欧几里德距离。每个蚂蚁在使用路径上的信息素的同时也会不断分泌信息素，因此路径上的信息素将不断积累。为了防止过多的信息素导致启发信息泛滥，在每个蚂蚁采取一步或完成一个周期之后更新路径上的信息素，并且从t+1时刻获得路径上的信息素，如式(3)所示

τij(t+1)=(1-ρ)τij(t)+ρΔτij(t)

(3)

式中：ρ为信息素挥发系数，主要模拟蚂蚁信息素随时间的自然挥发；1-ρ为信息素残留因子；Δτij(t)为循环路径(i，j)上信息素的增量。当信息素更新策略时，有不同的计算方法。如式(4)所示为蚂蚁循环模型计算方式

(4)

式中：Q为信息素的强度；Lk为蚂蚁在此循环中所采用路径的总长度。

2 改进蚁群算法

2.1 改善初始信息素

基本蚁群算法的信息素值在算法的初始阶段是固定的，蚂蚁在初始路径搜索中有一些盲目性，因此算法的搜索时间将会增加。鉴于此本文提出了一种改进的信息素方法，该方法根据当前节点、下一节点和起始点连接之间的相对距离计算初始信息素，如式(5)所示

(5)

其中，dSE为从起点到终点的欧几里德距离；dSi为从起点到当前节点的欧几里德距离；dij为当前节点和下一个节点之间的欧几里德距离；djE为从下一个节点到终点的欧几里德距离；C为下一个节点的集合；a0为常数。从式(5)中可以看出，当dSi+dij+djE越小，路径上的初始信息素越大。针对这一现象，根据位置关系设置了不均匀分布的初始信息素，避免了算法初始搜索的盲目性，进一步提高了搜索速度。

2.2 改进启发式信息功能

基本蚁群算法的启发式信息值与从下一个节点到目标点的距离成反比，从而驱动蚂蚁选择短距离路径。然而在不考虑当前节点和下一节点的位置的情况下，所选路径不一定是最短路径，并且在后期搜索阶段，为了加快收敛速度，启发式信息对路径选择的影响将会削弱。因此本文提出了一种通过引入阻尼系数来改进启发式信息函数的方法，如式(6)所示

(6)

其中

(7)

式中：NCmax为最大迭代次数；NC为当前的迭代次数。

2.3 改进信息素更新规则

信息素更新主要用于模拟天然蚂蚁信息素随时间的积累和自然挥发。目前对于信息素的更新主要有本地更新和全局更新两种方式，本文结合最大-最小蚁群系统(MMAS)[12]的基本模型和精英蚁群算法，对信息素更新规则进行了改进。

在一个蚂蚁完成循环后，可根据式(3)、式(4)实现本地更新路径。在所有蚂蚁完成迭代后，所有路径上的信息素都会更新，且所有完整路径都可以找到最佳解决方案和最差解决方案如式(8)所示，通过该式可有效增强当前最优解对后续迭代的指导作用。另外，对最差解决方案的惩罚可用于减少最差路径对后续迭代的误导效应，从而该算法将收敛速度加速到全局最优解

(8)

式中：Lbest是当前最佳路径的长度；Lworst是当前完整路径中最差路径的长度。为了避免算法停滞，将信息素的范围设置为[τmin，τmax]，如式(9)所示

(9)

2.4 改进状态转换规则

为了提高搜索效率和算法质量，使用伪随机状态转换规则。设蚂蚁k在t时刻位于节点i，则在t+1时刻蚂蚁k的位置为

(10)

其中，q0为转换率，范围为(0,1)，q为随机数，当q≤q0时，下一个节点直接由信息素浓度最大值和启发式信息来确定。

q0的值决定了确定性选择和随机选择模式的比率。如果q0值很大，则路径移位更可能是确定性模式，从而加速了收敛速度，但这种情况下会降低全局搜索能力。相反，如果q0的值较小，则路径移位更倾向于轮盘赌模式，这增加了路径选择的随机性并进一步增加了全局搜索能力。因此，q0值的设置对收敛速度和全局搜索能力有重要影响。本文提出了一种新的自适应计算q0的方法，通过迭代次数NC和当前最佳路径长度Lbest来确定q0值，如式(11)所示，其中b为(0,1)之间的常数。

(11)

为了进一步防止过早收敛到局部最优解并停滞，建立迭代次数阈值N0。当迭代次数NC小于N0时，q0值为b；否则自适应地计算q0的值。

2.5 解决死锁问题

当环境更加复杂时，蚂蚁可能会陷入无路的状态，即死锁。如图1所示，环境中的P1位置是一个“陷阱”，当蚂蚁走进那里时，它无法移动到另一个位置。虽然在P2位置没有明显的陷阱，但如果蚂蚁按图片路径行走最终也会出现死锁。

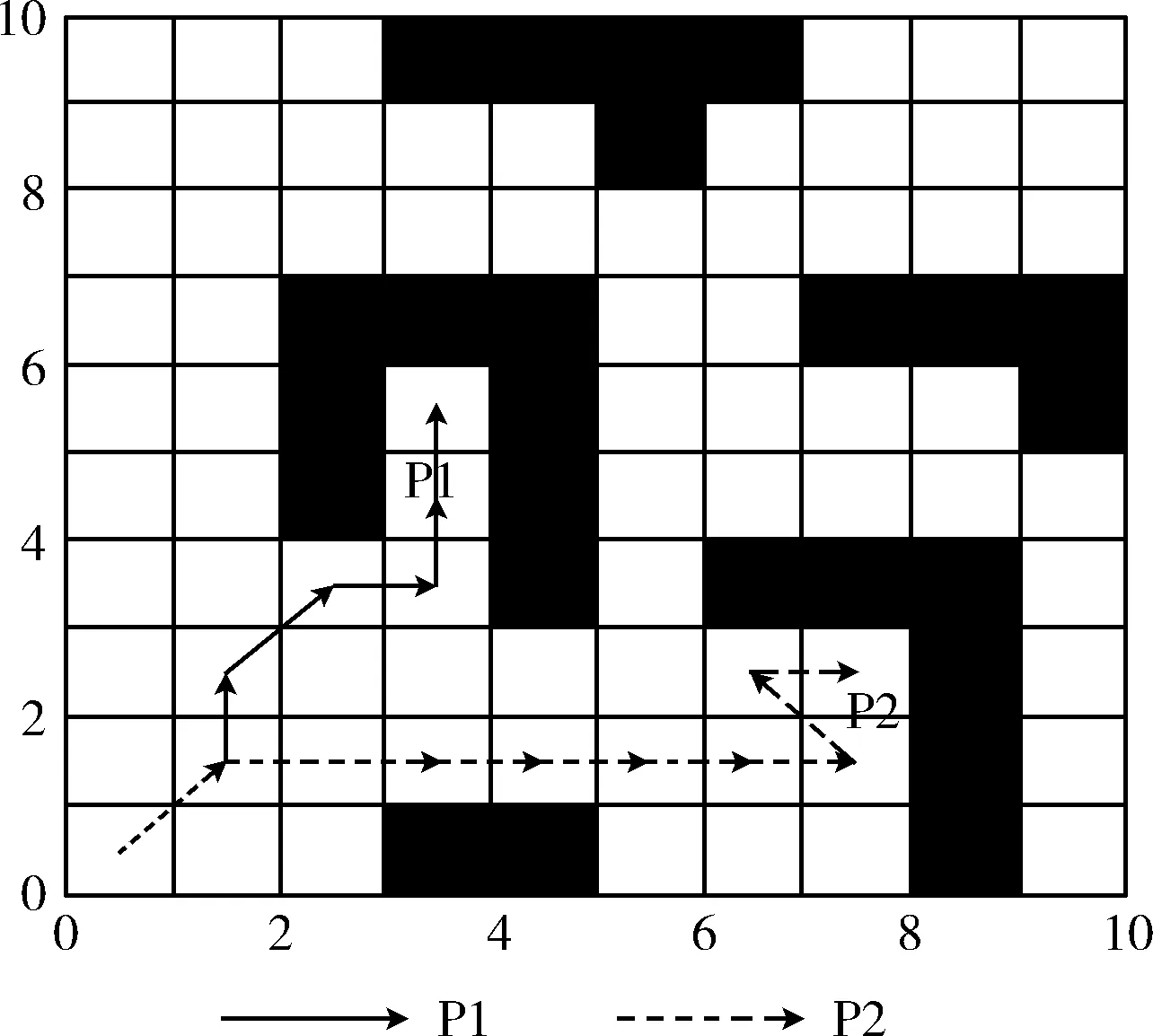
图1 死锁状态

针对僵局问题，在图1中P1位置需要后退两步才能摆脱它，计算复杂性将成倍增加。在本文中，使用了一种折衷方法，它可以杀死处于死锁状态的蚂蚁，并计算进入同一死锁点的蚂蚁数量nLost(i，j)，不完整路径的最后两步将由式(12)惩罚

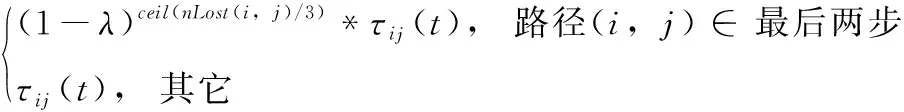
(12)

式中：λ为惩罚因子，其值为(0,1)之间的常数。很容易看出，同一条路径中的蚂蚁越多，对路径的惩罚就越大，后续蚂蚁通过这条路径的概率就越小，从而大大减少了失去的蚂蚁数量。

3 改进的蚁群算法在路径规划中的应用

将改进的蚁群算法应用于路径规划。具体步骤如下：

步骤1 初始化参数。其中包括起始位置S，目标位置G，蚂蚁数m，最大迭代次数NCmax，迭代次数NC，信息素强度Q，信息素启发式因子α，期望启发式因子β，死锁惩罚因子λ。其中，初始化目标位置S、目标位置G由实验网格环境决定，蚂蚁数m=50，最大迭代次数NCmax=100，信息素强度Q=100，α、β、λ作为变量根据实验对象分别进行设置。

步骤2 计算初始信息素。其中常数a0=0.5，将起点到当前节点的欧几里德距离dSi、当前节点和下一个节点之间的欧几里德距离dij、下一个节点到终点的欧几里德距离djE分别代入式(5)中计算初始信息素。

步骤3 路径选择。假设蚂蚁k在t时刻位于节点i处，则利用式(1)由路径(i，j)的信息素值τij、信息素激励因子α计算出蚂蚁选择下一节点的概率，然后利用式(10)计算蚂蚁在t+1时刻的路径选择。

步骤4 更新信息素和启发式信息。当蚂蚁建立完整路径时，对信息素和启发式信息进行更新，其中信息素可将信息挥发系数ρ、信息素残留因子1-ρ、信息素的增量Δτij(t)代入式(3)中进行更新，其中信息素的增量Δτij(t)由式(4)计算得到，启发式信息可由式(6)更新。

步骤5 死锁解决方案。当蚂蚁创建一条不完整的路径时，此时需要对所创建的死锁路径上的信息素利用惩罚因子λ进行惩罚，根据死锁发生的具体路径位置利用式(12)进行惩罚，当死锁被惩罚后转到步骤3并继续循环执行直到完成搜索。

步骤6 信息素的全局更新。在所有蚂蚁完成搜索之后，需要找到该迭代中所有完整路径的最佳路径和最差路径，并根据式(3)和式(8)增强最佳路径上的信息素，削弱最差路径上的信息素。

步骤7 自适应调整q0。当迭代次数Nc大于迭代阈值N0时，可由当前最佳路径长度Lbest、最大迭代次数NCmax、从起点到终点的欧几里德距离dSE通过式(11)计算新的状态转移率q0以更新状态转移规则。

步骤8 搜索结束。确定是否满足结束条件，如果满足，则输出最佳路径长度，否则清除禁忌清单，让NC=NC+1，然后转到步骤3并继续循环执行，直到满足结束条件或达到最大迭代次数。如图2所示为基于改进蚁群算法的路径规划的具体过程。

图2 改进蚁群算法的路径规划的具体过程

4 模拟实验和分析

为验证所述改进势场蚁群算法的有效性，在Matlab R2010a中进行仿真实验，计算机操作系统为Windows 7，CPU为core i5-650，内存为8 GB，仿真环境分别为10×10、20×20、30×30的平面栅格环境。同时，为了验证本文算法的优越性，在相同环境中将本文算法所得结果分别与文献[13]和文献[14]中改进蚁群算法的结果进行比较。

4.1 模拟环境的建立

为了便于蚁群算法搜索最优路径，本文采用网格法建立二维移动环境空间，网格按从上到下，从左到右的顺序编号。其中障碍网格称为不可行网格，无障碍网格称为可行网格。为了便于算法的实现，蚂蚁在行进过程中当遇到障碍网格时，算法默认将其标注为“1”，无障碍网格标注为“0”，从而将网格图转换为0和1分布的二维电子地图，如图3所示。

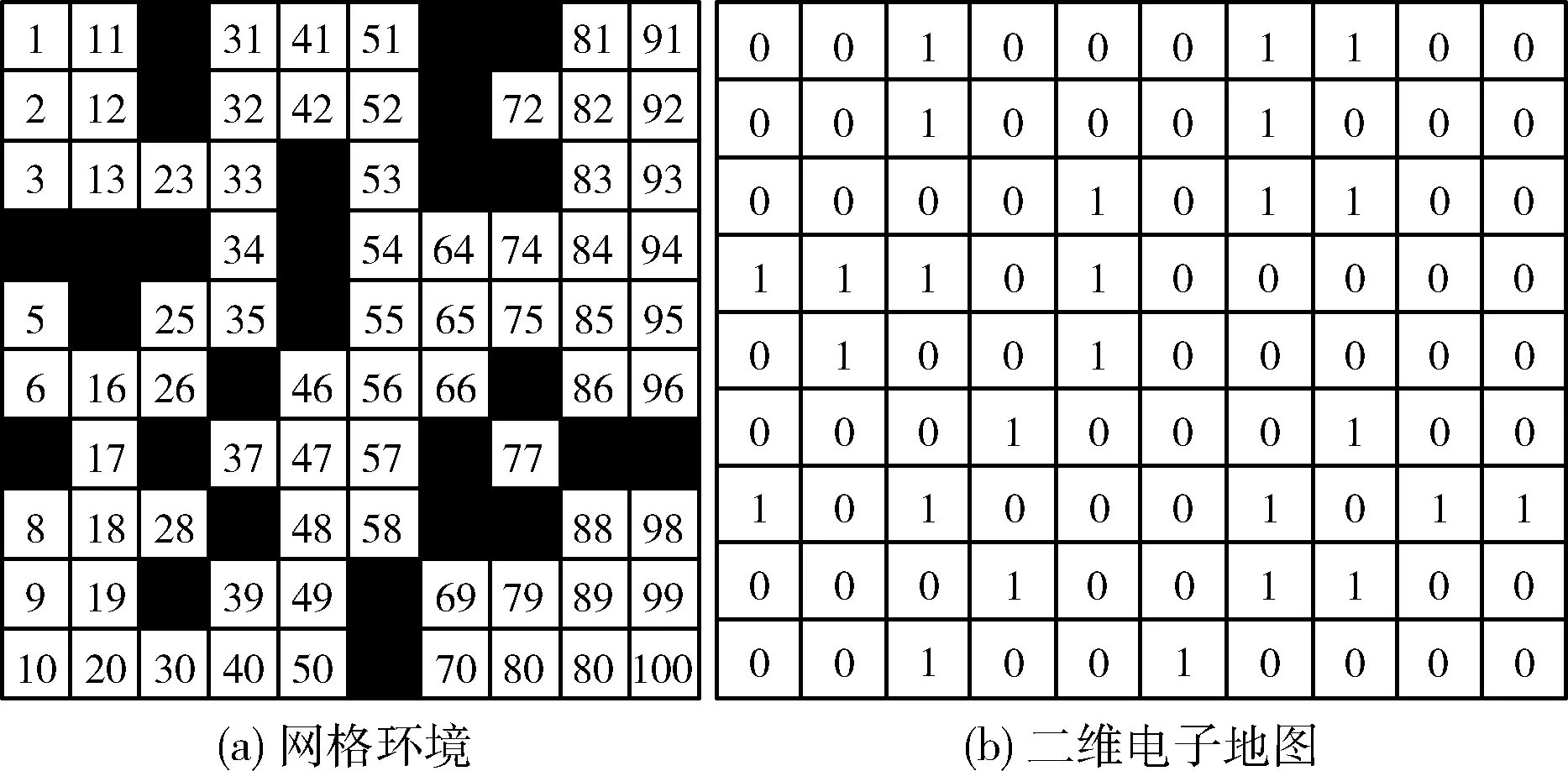
图3 网格图和相应的电子地图

通过式(13)确定网格编号与坐标之间的数学对应关系

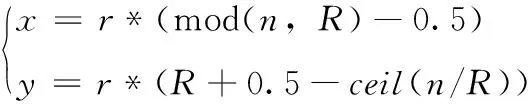
(13)

其中，r为网格的比例，由机器人的几何尺寸决定；n为网格号；R为网格的行数；mod函数为余数函数；ceil函数是向右舍入函数。

4.2 参数优化选择

蚁群算法的参数选择直接决定了算法的性能，常用的方法有遗传算法，粒子群算法(PSO)，三步法，经验和实验方法等。但到目前为止，还没有完美的方法直接确定参数的最优组合。为了降低算法的复杂度，本文采用经验和实验方法，通过设置不同的参数进行仿真实验，分析实验结果的优缺点，选择最优参数组合。

测试方法为每个参数设置一组值，在每个实验中，只有一个参数被更改，其它参数为常量。分别测试迭代次数，最佳路径长度和丢失的蚂蚁数量。本文仅介绍启发式因子α，期望启发式因子β，挥发系数ρ和死锁惩罚因子λ的最优组合。其它参数可以以相同的方式执行。

使用环境1(如图3(a))作为组合实验的测试环境，参数设置如下：

m=50，NCmax=100，Q=100，β=6，ρ=0.2，λ=0.2，N0=5，q0=0.3。当α=0.8，α=0.9，…，α=2.0时，分别测试算法的迭代次数，最佳路径长度和丢失的蚂蚁数量，实验结果如图4所示。实验结果表明，当α很小时，改进的蚁群算法无法搜索全局最优解；当α∈[1,1.2]时，它具有更好的收敛速度和搜索全局最优解的能力。随着α的进一步增加，算法的收敛速度逐渐增大，但全局搜索能力逐渐减弱，更容易陷入局部最优解。总体而言，与基本蚁群算法相比，本文改进的蚁群算法大大提高了收敛速度、全局最优解搜索能力和丢失蚂蚁数的性能指标。

图4 启发式因子与迭代次数、最佳路径长度、丢失蚂蚁数的关系

在同一环境中，设置如下参数：m=50，NCmax=100，Q=100，α=1.1，ρ=0.2，λ=0.2，N0=5，q0=0.3。当β=1，β=2，…，β=9时进行一系列实验。实验结果如图5所示。实验结果表明，无论β如何变化，它都具有更快的收敛速度和更少的蚂蚁损失，并且当β∈[4,7]时，有最佳的性能指标。最小迭代次数为8.7次，最佳路径长度为13.898，丢失的蚂蚁数为28.2。

当ρ=0.1，ρ=0.2，…，ρ=0.9时，分别测试算法的迭代次数，最佳路径长度和丢失的蚂蚁数。实验结果如图6所示。当ρ增加时，收敛速度更快，失去的蚂蚁更少，但路径更长。当ρ在[0.1,0.2]之间时，算法具有最佳性能指标。全局最优路径长度为13.898，迭代次数为9.6，丢失蚂蚁数为58.4。

当λ=0.1，λ=0.2，λ=0.3……，λ=0.9时，进行相同的实验。实验结果如图7所示。结果表明当λ∈[0.2，0.5]时，具有最佳性能指标，最小迭代次数为7.9，最佳路径长度为13.898，丢失蚂蚁数为39.3。总之，改进的蚁群算法大大提高了基本蚁群算法的性能指标。当α∈[1,1.2]，β∈[4,7]，ρ∈[0.1,0.2]，λ∈[0.2，0.5]时，有更好的综合性能指标。

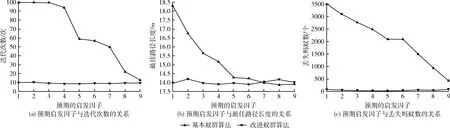
图5 预期启发式因子与迭代次数、最佳路径长度、丢失蚂蚁数的关系

图6 信息素挥发系数与迭代次数、最佳路径长度、丢失蚂蚁数的关系

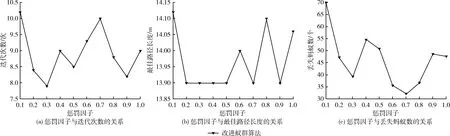
图7 惩罚因子与迭代次数、最佳路径长度、丢失蚂蚁数的关系

4.3 与其它算法进行比较

4.3.1 20×20情况(环境2)

为了验证所提出的算法的有效性与优越性，将其与文献[13]的算法在环境2(如图8(a))情况下进行对比实验，实验参数设置为：m=50，NCmax=100，Q=100，α=1.1，ρ=0.2，β=7，λ=0.2，N0=5，q0=0.3。如图8所示为对比实验仿真结果，图8(a)中的实线是本文算法的规划路径，虚线是参考文献[13]中的算法路径。为避免偶然情况，重复了10次实验，表1为平均结果。从图8和表1可以看出，文献[13]中的算法比本文算法具有更快的收敛速度和更少的运行时间，但本文算法在最优路径搜索的性能指标上具有更大的优势，且丢失的蚂蚁数量更少。本文算法的最优路径长度收敛到30.968，而文献[13]中算法的平均路径长度为35.6573，这进一步说明了本文的算法更稳定。

4.3.2 30×30情况(环境3)

为了验证复杂环境的有效性和优越性，将其与文献[14]的算法在环境3(如图9(a))情况下进行对比实验，仿真结果如图9所示。图9(a)中的实线是本文算法的规划路径，虚线是文献[14]中算法的规划路径，表2给出了在相同参数下重复10次实验的平均值。

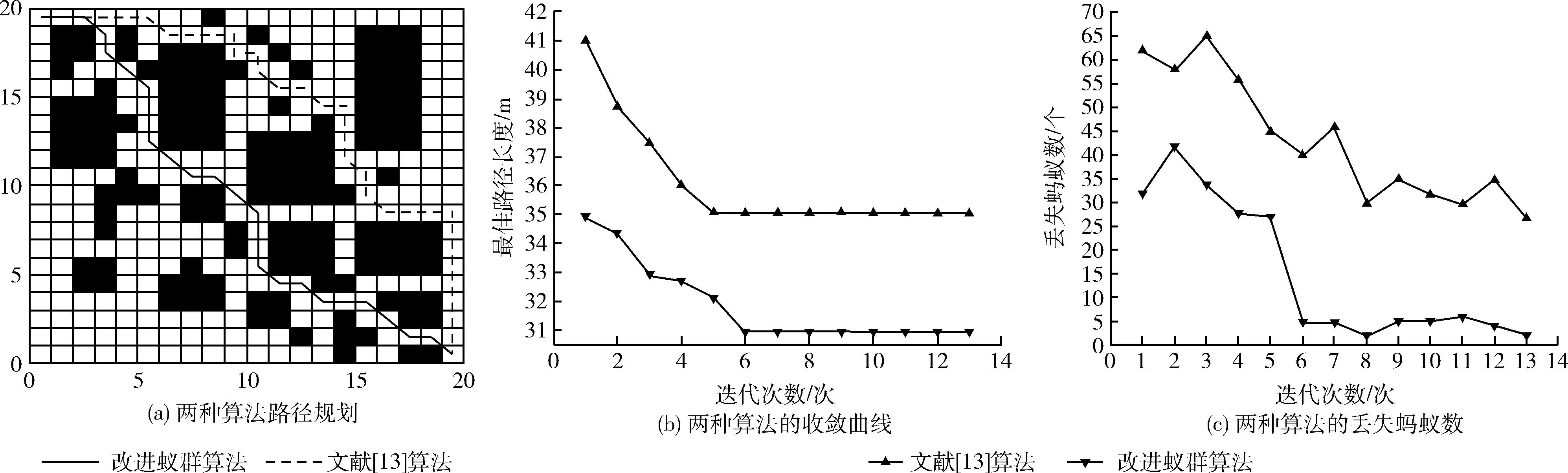
图8 两种算法在路径规划中的比较结果

表1 两种算法在路径规划中的比较结果

从实验结果上来看，在复杂的环境中本文算法仍然可以快速搜索最优路径。文献[14]中算法的最佳路径长度为48.425，而本文的最佳路径长度为44.522，路径长度缩短3.903；文献[14]中的平均迭代次数为59次，本文算法的平均迭代次数为22.1次，收敛速度提高了近3倍且丢失的蚂蚁数量仅占文献[14]中算法的三分之一。在运行时间上，本文算法较文献[14]中的算法更长，但考虑到算法的性能指标，本文算法可以在运行时间上做出一点牺牲，从而获得更好的路径长度和更快的收敛速度。

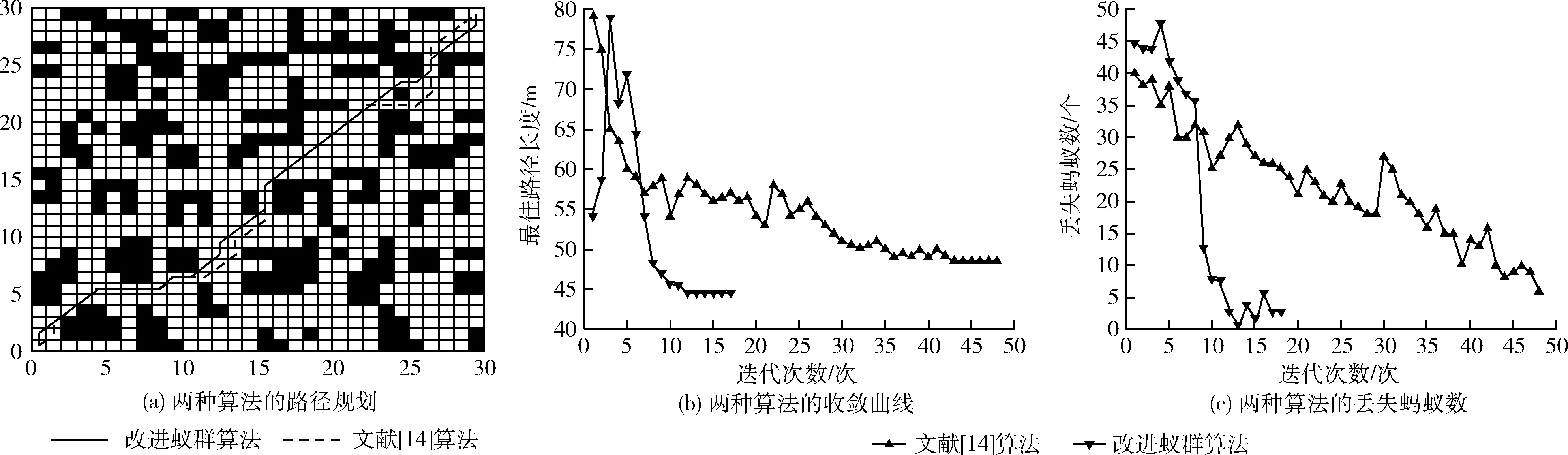
图9 两种算法在路径规划中的比较结果

表2 两种算法在路径规划中的比较结果

综上所述，本文将改进的蚁群算法与文献[13]、文献[14]的算法进行了比较。本文提出的改进算法能够自适应地调整了伪随机状态转移比例基数，以改进路径选择规则，启发式信息函数和信息素更新规则，进一步提高了收敛速度和全局搜索能力，大大减少了蚂蚁丢失的数量，具有很大的优越性和实用性。

5 结束语

路径规划是当前机器人在复杂环境下行进的关键技术，蚁群算法作为一种仿生算法能够有效实现机器人的路径规划。针对基本蚁群算法在路径规划中存在的收敛速度慢、搜索效率低的问题提出了一种改进的蚁群算法。实验中将改进的蚁群算法应用于机器人路径规划，并通过实验和经验方法确定算法参数的最优组合。通过模拟多个移动环境，并与其它算法进行比较，实验结果表明改进的蚁群算法有效解决了算法初期盲目搜索的问题，提高了收敛速度，验证了该算法的有效性和优越性。