基于深度学习的地震剖面图像超分辨率重建

邓梦迪，贾瑞生+，田 煜，刘庆明

(1.山东科技大学 计算机科学与工程学院，山东 青岛 266590；2.山东科技大学 山东省智慧矿山信息技术省级重点实验室，山东 青岛 266590)

0 引 言

地震剖面图像可以显示断层或者是剖面信息，为了提高其分辨率，通常需要增加勘探道数来加密地震数据，大大增加勘探成本。超分辨率重建技术可直接实现低分辨率图像到高分辨率图像的映射，具有十分重要的工程应用价值。

目前，图像超分辨率重建技术[1,2]通常可分为3类：基于插值的方法[3,4]、基于重构的方法[5]和基于学习的方法[6,7]。基于插值的方法[8]最为简单且运算速度快，但容易造成图像模糊。基于重构的方法[9]容易产生伪影等工效应。基于学习的方法取得了较为理想的效果，成为超分辨率重建领域中研究的热点。Yang等提出了基于稀疏表示的超分辨率重建(SCSR)方法[10]，该算法对重建图像的质量有一定的提升。Dong等提出了应用卷积神经网络的单帧图像超分辨率重建(SRCNN)算法[11]，该算法应用3个卷积层重建高分辨率图像特征，重建效果优于其它传统算法，但重建速度慢。随后，Dong等对SRCNN进行改进，提出了一种基于反卷积的快速图像超分辨率重建(FSRCNN)方法[12]。Shi等提出了基于亚像素卷积层的超分辨率重建(ESPCN)方法[13]。

地震剖面图像纹理单一且边界不够明显，采用传统重建方法容易丢失其高频信息，为此，本文提出一种基于深度学习的地震剖面图像超分辨率重建方法，在网络模型中加入双通道注意力机制块，充分提取图像特征并有选择地进行高频增强，取得了较好的重建效果。

1 理论基础

1.1 双通道卷积

传统的单通道卷积网络卷积核尺寸单一，导致特征提取不够充分，双通道卷积可以在两个通道上分别采用不同尺寸的卷积核，提取特征图在不同尺度下的特征，有利于图像的后期重建。为了降低算法复杂度，在每个尺度卷积前均采用尺寸为1×1的卷积核进行降维。图1为单通道卷积和双通道卷积的结构，其中M×M，N×N为卷积核尺寸，C1，C2为输出特征图通道数。

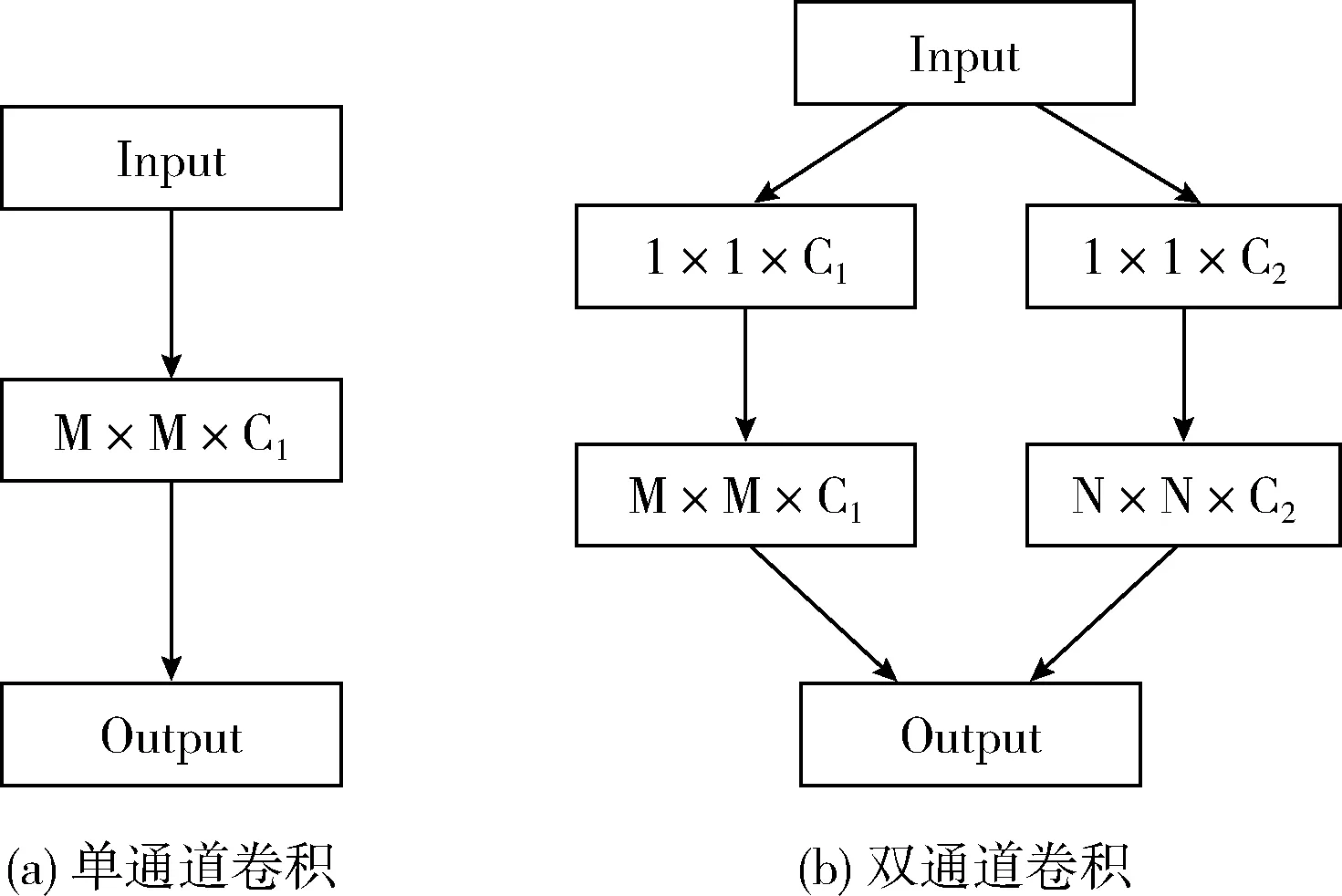
图1 单/双通道卷积结构

1.2 注意力机制

阶段学习的卷积操作是将通道和空间信息混杂到一起提取图像的纹理特征，卷积后特征较为混杂，神经网络不能识别哪些通道所含高频信息较多。在网络中添加注意力机制块可以使神经网络更加关注具有足够高频细节的通道和区域，在一定程度上加快网络收敛速度。注意力机制块由两个卷积层和两个激活层级联而成，同时学习不同通道和不同区域相应的描述符，并给不同通道和不同区域分配不同的权重。注意力机制块结构如图2所示。

图2 注意力机制块

S=f(w2((w1x+b1))+b2),S∈RH*W*C

(1)

其中，w1，w2分别代表注意力机制块中第一层和第二层卷积的权重，b1,b2分别代表其偏置。第一层卷积完成因子为8的降维，经第一层卷积后得到的特征图通道数为C/8，第二层卷积完成因子为8的升维，特征图通道数重新恢复为C。f(·)代表sigmoid激活函数，(·)表示Prelu激活函数。将缩放后的描述符S与原输入进行逐通道Hadamard相乘，得到通过注意力机制块的特征表示。

2 本文方法

基于卷积网络的超分辨率重建算法通常可分为以下4个步骤：①预处理数据集，构造网络训练集；②设计超分辨率重建网络模型；③利用训练集训练网络，优化网络参数；④利用训练好的网络模型重建高分辨率图像。

2.1 网络模型

网络模型的结构直接影响重建图像的精度，传统超分辨率重建网络特征提取不够充分且易丢失重建图像的高频信息，为了解决此问题，本文在网络模型中引入双通道注意力机制块。网络模型结构如图3所示，可分为特征提取、非线性映射和重建3个阶段。

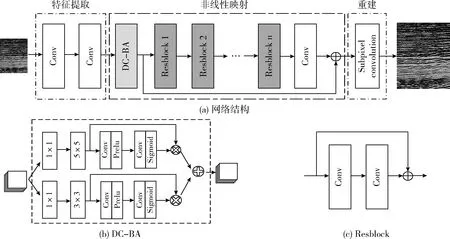
图3 本文超分辨率重建网络结构

(1)特征提取阶段。从低分辨率图像中提取图像块，并将其分别表示成一个高维向量，这些向量组成一组特征图，其数量和向量的维度相等。该阶段卷积层的参数设置为3×3×128，即128个尺寸为3×3的卷积核。

(2)非线性映射阶段。非线性映射阶段的结构是影响超分辨率重建性能最重要的部分，用于实现低分辨率图像块到高分辨率图像块的特征映射。本文方法的非线性映射由双通道注意力机制块和若干层卷积级联实现。双通道注意力机制块结构如图3(b)所示，首先采用1×1的卷积核降低特征图维度，然后在两个通道上分别采用3×3×64和5×5×32的卷积核提取图像特征，最后连接注意力机制块，有选择地进行高频增强。由于该阶段卷积层数较多，容易导致梯度消失现象，为解决此问题，采用残差网络结构，一定程度上提高了训练收敛速度，残差块结构如图3(c)所示，卷积层参数设置为3×3×64。

(3)重建阶段。采用亚像素卷积层实现高分辨地震剖面图的重建。亚像素卷积操作具体可分为两部分，首先采用尺寸为3×3，数量为r2(r为图像放大倍数)的卷积核进行卷积操作，然后将r2个大小为H×W的特征图重新排列成一幅rH×rW大小的高分辨率图像。亚像素卷积操作可表示为

YSR=Fn(Y)=PS(Wn*Fn-1(Y)+bn)

(2)

其中，Fn-1(Y)为经非线性映射后输出的特征图，Wn和bn表示可学习的网络权重和偏置,PS表示亚像素卷积操作，YSR为重建得到的高分辨率图像。

网络中的卷积操作可表示为

Fl(Y)=f(Wl*Y+bl),l∈(1,n-1)

(3)

其中，Y为网络输入，Wl，bl分别代表第l层卷积的权重和偏置，f(·)表示激活函数。为了充分利用边缘信息，卷积前对图像边缘进行零填充，使得重建后的图像大小为输入图像的整数倍。本文超分辨率重建算法的具体描述见表1。

2.2 训 练

本文选择Prelu作为网络激活函数，使用基于L2范数的损失来指导网络学习，使用的损失函数[14]的表达式为

表1 本文超分辨率重建算法描述

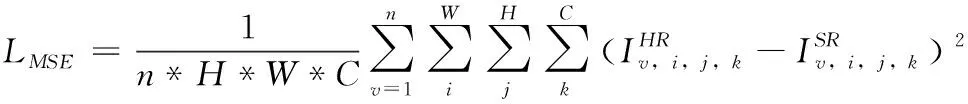
(4)

其中，n表示每个batch中训练样本的数量。H*W为特征图的尺寸，C为特征图通道数，Iv,i,j,k为第v幅图像第k个通道位置为(i,j)的像素值，LMSE越小，说明重建图像与原始高分辨率图像的差异越小。训练采用反向传播的梯度下降算法进行优化。

3 实验结果及分析

3.1 实验环境及评价指标

实验测试所用计算机配置为Intel Core i7-3770U@3.40 GHz CPU,配置NVIDIA GeForce GTX 1060 GPU，内存为12 GB。实验平台搭载的操作系统为64位Windows 7系统，Matlab 2012b、CUDA Tookit 8.0、Cudnn 5.0和caffe[15]深度学习框架。

本文选用峰值信噪比(PSNR)[16]和结构相似度(SSIM)[16]作为重建图像质量的客观评价指标。PSNR用于定量计算重建图像跟原图之间误差，其值越高，说明重建图像失真越小；SSIM说明重建图像结构与原图结构的相似程度，SSIM的值越接近1，说明生成的重建图像与原图像结构越相似，效果越好。

3.2 数据集

为更好学习地震剖面图像的纹理特征，本实验选择了300幅地震剖面图像，从中选取270幅地震剖面图像作为训练集，30幅作为测试样本。由于地震剖面图像没有官方数据集，本实验数据集均在网络数据库中获得。训练样本由低分辨地震剖面图像和高分辨率地震剖面图像(标签)两部分组成，为了对原始的270幅原始训练样本进行扩充，采用大小为17×17的滑动窗口对降质图像进行切块，得到17×17大小的图像块作为低分辨率图像块，采用大小为17r×17r(r为目标放大倍数)的滑动窗口对高分辨率图像切块，得到17r×17r大小的高分辨率图像块(标签)，原始训练集如图4所示。

图4 原始训练集图像部分展示

3.3 网络层数设置

网络的深度是影响超分辨率重建效果的重要因素之一。适当增加网络层数，能够增强网络的非线性映射能力，提取更多纹理细节特征，便于后期重建，但是随着网络的加深，在训练过程中可能会出现难以收敛的现象。本文算法采用残差结构，可以加快网络收敛，避免网络过拟合的现象。当放大倍数为3时，分别训练及测试层数为14、16、18的卷积网络模型，即分别包括3、4、5个残差块，实验将LR图像块和对应标签作为网络的输入，训练过程采用SGD优化器，动量设置为0.9，学习率设置为0.0001，训练迭代5×105次。图5为测试集的平均PSNR值随迭代次数增长的曲线。从图中可以看出，18层网络模型重建性能最好。对比不同深度下测试集的PSNR均值和SSIM均值，见表2，结果说明了18层网络重建图像的PSNR和SSIM均为最高，所以本实验网络模型设计为18层。

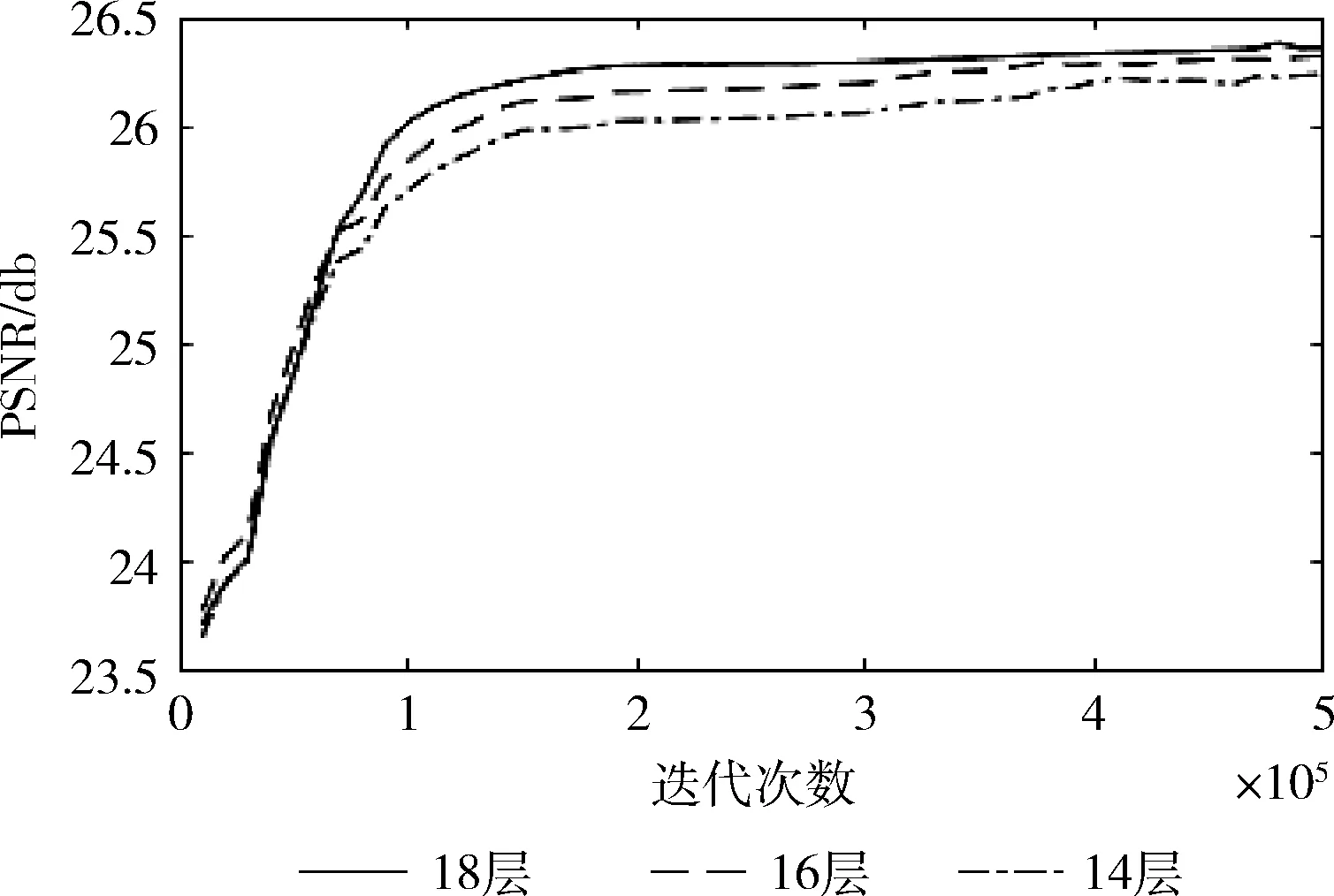
图5 测试集图像的PSNR平均值在不同层数下随迭代次数的变化

表2 不同深度下测试集的平均PSNR和SSIM

3.4 实验结果及分析

在测试集中随机选取一幅测试图6(a)，分辨率为297×258，经3倍下采样处理后得到分辨率为99×86的低分辨率图6(b)，由于图像太小导致无法看清图像中的纹理细节信息。将图6(b)由人工放大(不改变图像分辨率)得图6(c)，可见图6(c)图像细节模糊，使得后续的地震解释工作变得困难。本文采用超分辨率重建的方法重建低分辨率地震剖面图像，如图6(d)所示，可较为精确的重构图像细节纹理信息。

图6 超分辨率重建实验效果

为了体现本文算法的有效性，将本文算法同基于插值的Bicubic算法、基于稀疏表示的ScSR算法、基于卷积神经网络的SRCNN、FSRCNN和ESPCN算法进行对比。在测试集中随机选取3幅测试图像，将它们都进行3倍下采样处理得到LR图像，采用本文算法和对比算法进行重建并选取感兴趣的区域放大，实验效果对比如图7所示。从细节放大图中可以看到，传统的Bicubic算法重建图像边缘模糊，纹理细节不明显。ScSR算法图像边缘伪影现象较为严重。SRCNN、FSRCNN、ESPCN整体视觉效果优于Bicubic和ScSR,但是重建图像边缘处仍存在不同程度的伪影。对比上述算法，本文算法取得了更好的重建效果，重建图像的细节信息恢复更加完整，边缘更加清晰。

在3倍放大因子下，选取8幅测试图像进行重建并记录其PSNR值和SSIM值,如表3所示。可以发现本文算法的PSNR值和SSIM值均高于对比算法。为避免偶然性，在2、3、4倍的放大因子下分别训练神经网络并进行测试，表4为测试集的平均PSNR值和SSIM值。可以看出本文方法在不同放大倍数下，客观评测结果均优于其它对比算法，充分说明本文算法重建效果更好。

3.5 速度比较

为了测试本文算法的时间性能，在测试集中随机选择5幅图像，采用本文算法及基于神经网络的对比算法进行重建，各方法的重建时间见表5，从表5中可以看出，本文算法较SRCNN、FSRCNN、ESPCN方法相比，重建速度略慢。

4 结束语

本文将超分辨率重建技术应用到地震剖面图像处理领域，在地震数据采集过程中可采用较少传感器采集地震数据，成像后采用超分辨率重建技术重建高分辨率地震剖面图像，有效节约勘探成本。本文网络模型共有18层，在高层网络中加入双通道注意力机制块，提高了重建精度。实验结果表明，本文算法的PSNR、SSIM均高于现有的几种典算法，重建图像细节更丰富，边缘更加锐利。但该算法由于网络层数的增加导致重建速度较慢，下一步工作的重点是在保证重建图像精度的条件下降低算法复杂度。

图7 不同方法重建效果展示

表3 不同方法重建测试图像的PSNR/db和SSIM

表4 不同放大倍数时各方法在测试集上的平均PSNR/db和SSIM

表5 不同方法重建时间/s