自适应图嵌入的鲁棒稀疏局部保持投影

占善华，武继刚，房小兆

(1.广东工业大学 计算机学院，广东 广州 510006; 2. 广东司法警官职业学院 信息管理系， 广东 广州 510520)

0 引 言

近些年，学者们提出了大量的维度约简方法。这些方法可简单的分为3大类：有监督、无监督和半监督方法[1,2]。有监督和半监督方法一般利用标签信息来指导转换矩阵的学习[3,4]。而无监督方法旨在不利用的任何标签信息的条件下自适应地挖掘隐藏在数据中的信息来学习特征转换矩阵[5-7]。线性鉴别分析(linear discriminant analysis，LDA)和主成分分析(principle component analysis，PCA)是最具代表性的有监督和无监督降维方法[5,8]。但这两种方法不能发现数据的非线性结构。

基于高维数据一般都分布于低维流行空间的假设，大量基于流行学习的方法被提出来用于解决非线性维度约简问题。例如，局部保持投影(locality preserving projection，LPP)。近邻保持嵌入(neighborhood preserving embedding，NPE)。但是，这两种方法都对近邻参数的选取较为敏感。为了克服这个问题，稀疏保持投影(sparsity preserving projection，SPP)被提了出来。但其缺点是图构建方法具有较大的运算代价，限制了其在大尺度数据情形下的应用[9]。为了克服这个缺陷，Yang等提出构建L2-graph来代替L1-graph的非线性维度约简方法，称之为基于协同表示的投影学习(collaborative representation based projection，CRP)[9]。近年来，低秩表示受到了极大的关注[10]。Zhang等提出了一种低秩保持嵌入方法来应对非线性维度约简。Wong等基于低秩表示也提出了一种新颖和简单的非线性维度约简方法，称之为低秩嵌入(low-rank embedding，LRE)[4]。与LRPE相比，LRE将投影学习和图构建融入到一个联合框架，能够学习到一个全局最优投影矩阵。在文献[11]中，低秩和稀疏被同时用于指导投影矩阵的学习。但是，因为这些方法在图的构建或投影矩阵的学习过程中均等地对待所有特征，这些方法对噪声和离群点较为敏感。

针对上述问题，本文提出一种无监督维度约简方法，称之为自适应图嵌入的鲁棒稀疏局部保持投影(robust sparse locality preserving projection with adaptive graph embedding，RSLPP_AGE)。该方法旨在设计一个联合优化框架来自适应获得数据的全局最优投影矩阵和仿射图。该方法并不直接从原始高维数据中学习仿射图，而是从更具鉴别性的低维表征数据中学习，使其对噪声更具鲁棒性。为了捕获数据的全局结构，引入了一个PCA约束性，使其能够保持数据的主要信息。为了进一步提高对噪声的鲁棒性，在投影矩阵上引入了一个行稀疏约束，使其能够自适应地从复杂的高维数据中选择最重要的特征来指导投影矩阵和仿射图的学习。

1 局部保持投影

局部保持投影(LPP)是一种非常具有代表性的基于流行学习的维度约简方法。对于训练集X=[x1,x2,…,xn]∈Rm×n，其中一列表示一个样本，LPP首先从训练集中构建近邻图W∈Rn×n，然后使用如下目标函数来学习用于非线性降维的投影矩阵Q∈Rm×d

(1)

(2)

其中，ψ(xj)表示样本第xj的k近邻集合。

问题(2)是典型的特征值分解问题。从模型(2)中能够发现，LPP能够在维度约简过程中保持数据的近邻结构。

2 自适应图嵌入的鲁棒稀疏局部保持投影

2.1 学习模型

如前所述，LPP能够很好保持数据的局部近邻结构。但是，其性能取决于所构建的近邻图W的质量。一般的，原始数据含有较多的冗余特征和噪声，从原始数据中往往难以发现数据的本质结构。而在不精确的仿射图上指导下，难以得到合理的投影矩阵Q。此外，LPP将投影矩阵学习和仿射图学习分为两个独立的步骤，难以得到全局最优的投影矩阵。LPP还忽略了数据的全局结构，表明其并没有充分利用数据的结构信息来指导投影矩阵的学习，因此限制了其性能。基于此，本文提出了改进方法。

首先，为了捕获数据的全局结构，我们将PCA约束项引入到LPP，并提出了如下学习模型

(3)

其中，X=PQTX+E是PCA的变体形式[3]，E∈Rm×n表示误差或噪声，λ2是一个正值惩罚项参数。引入PCA变体项使得方法能够同时捕获数据的全局和局部结构信息。其次，原始高维数据可能含有大量冗余特征和噪声，一种合理的模型应该能够自适应地从中选择更具鉴别力的特征来指导模型的训练。基于此，本文方法引入了具有特征选择能力的l2,1范数约束

(4)

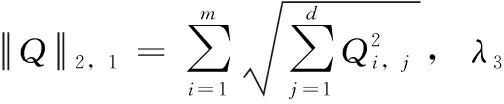
最后，考虑到预定义的图W并不能保证投影矩阵Q的全局最优性，我们对模型(4)进一步做如下改进来学习全局最优的投影矩阵

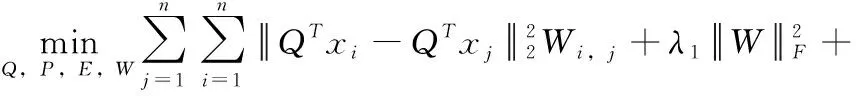
(5)

其中，λ1是正值惩罚项参数，用于平衡对应项在模型训练中的作用。式(5)即为本文提出的学习模型。

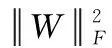
2.2 模型优化求解

问题(5)包含4个未知参数，难以求解。本节利用交替迭代方向乘子法来对其进行优化以得到其局部最优解[10,11]。问题(5)的拉格朗日函数表示如下

(6)

其中，μ和C分别是惩罚项参数和拉格朗日乘子。各变量的优化过程如下：

Q-Step：问题(5)关于变量Q的求解问题为

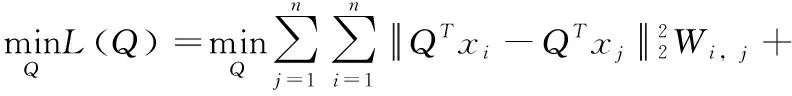
(7)

求L(Q)关于变量Q的偏导数，得到

(8)

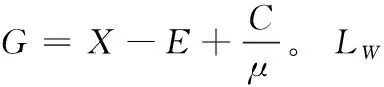
(9)

P-Step：在固定其它未知变量时，变量P的优化问题为

(10)

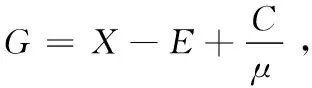
W-Step：关于变量W的优化问题为

(11)

(12)

从式(12)中能够发现，问题(12)关于变量W的各行是独立的。通过逐行求解W，可得到其最优解为[13,14]

(13)

E-Step：关于变量E的优化问题为

(14)

上式是一个典型的稀疏约束求解问题，通过求解上式，能够得到变量E的最优解为

E=Ωλ2/μ(X-PQTX+C/μ)

(15)

其中，Ω表示收缩算子(shrinkage operator)。

μ和C-Step：这两个变量的迭代方式表示如下

(16)

其中，μ0是常数。

RSLPP_AGE的优化步骤总结如下：

算法1：RSLPP_AGE (solving (5))

Input:Training dataX,parametersλ1,λ2,andλ3, dimensiond.

Initialization: Exploiting PCA to initialize data reconstruction matrixP,Q=P,E=0,C=0,μ=0.01,ρ=1.1,μ0=105.

while not converged do

UpdateQby using (9)；

UpdatePby solving (10)；

UpdateWby using (13) and then implementW=max(W,0);

UpdateEby using (15)；

UpdateCandμby using (16).

end while

Output:Q

3 计算复杂度与收敛性分析

计算复杂度：本节并不考虑一些基本矩阵运算的计算复杂度。事实上，算法1中仅含两个具有高计算复杂度的运算，即矩阵的逆运算和SVD运算。SVD运算的计算复杂度为O(d3)；对于维度为m×m的矩阵，其逆运算的计算复杂度为O(m3)[15,16]。因此，算法1中第Q和P的优化步骤的计算复杂度为O(m3)和O(d3)。对于其它步骤而言，能够发现它们并不包含复杂的运算，因此可以忽略这些步骤的计算复杂度。根据以上分析，考虑到d≪m，算法1总的计算复杂度为O(τm3)，其中τ表示算法的迭代步骤。

收敛性分析：如前所述，我们将一个复杂的非凸优化问题转换为了4个简单的凸优化问题，而我们又知道问题(5)的目标函数值在迭代中单调下降，目标函数值是有下界的。因此从问题(5)的单调性和有界性能够得出结论，算法1的优化过程能够收敛到一个局部最优解。

4 实验结果与分析

4.1 实验设置

数据集：Extended Yale B、CMU PIE和AR等3个人脸数据集和COIL20目标数据集被选取用于评价所提出的方法的有效性。Extended Yale B数据集包含2414张正面人脸图像，该数据库中的人脸含有不同的光照变换，共含有38类，每类含有59张-64张图像。CMU PIE人脸数据集含有11 554张图像和68类，这些样本从5个不同的角度下获得。AR人脸数据集是一个比较具有难的人脸数据集，该数据集上含有大量不同人脸表情、光照和遮挡(眼镜和围巾遮挡)的人脸图像。在本章，一个来自于120个类的含有3120张人脸图像的子集被选择用于测试。COIL20是一个比较流行的目标数据集，该数据集含有1440张图像和20个类。每一个目标含有72张不同角度的目标图像。图1展示了这些数据集的典型样例图像。

对于以上数据集，所有图像都被统一缩放为32*32的尺寸，然后为了提高计算效率，我们进一步使用PCA来降低特征维度，其中PCA降维率为98%，上述数据集降维后的特征维度尺寸分别为148，497，157和175[4]。

对比方法：本节与一些较为相关的方法进行对比，包括经典的NPE，SPP，PCA以及基于这些方法改进的稀疏PCA(sparse PCA，SPCA)[17]，LPP正交LPP(orthogonal LPP，OLPP)[18]，CRP[9]，低秩保持投影(low-rank preserving projection，LRPP)[19]，LRE[4]和LRPE[20]。在以上这些方法中，LPP，OLPP，NPE，SPP和CRP可视为基于局部结构信息的特征抽取方法。而其它方法都是基于全局和局部结构信息的方法。

图1 4种典型图片数据集

参考文献[7]的实验设置，在AR数据集上，我们从每类中随机选取4,6,8和12个样本作为训练样本，然后将其它样本作为测试样本。对于其它数据集，我们从每类随机选取10,15,20和25个样本作为训练样本，将其余的样本作为测试样本。我们将各种算法重复执行20次，然后将它们的均值结果进行对比。在这些数据集上的实验结果见表1-表4。

表1 各种方法应用在Extended Yale B数据集上的平均分类准确类对比

表2 各种方法应用在CMU PIE数据集上的平均分类准确类对比

4.2 实验结果分析

表1-表4的实验结果可以发现，与其它方法相比，所提出的RSLPP_AGE 在人脸分类和目标分类任务上都获得了最好的效果。此外，从这些表所列的对比结果还能发现：

(1)在人脸数据集上，即Extended Yale B，CMU PIE和AR数据集，基于流行学习的方法，如LPP，NPE，SPP，和CRP等获得了优于PCA的效果，然而，在COIL20数据集上，这些方法比PCA性能要差一些。这些实验结果表明人脸数据库可能含有非线性的流行结构，而基于流行学习的特征抽取方法在这些数据集上表现更好。

表3 各种方法应用在AR数据集上的平均分类准确类对比

表4 各种方法应用在COIL20数据集上的平均分类准确类对比

(2)在3个较为复杂的人脸数据集上，SPP，CRP，和LRPE获得了优于LPP和OLPP的性能。与LPP和OLPP相比，SPP、CRP和LRPE都利用了数据的表示结构来指导模型的训练。因此在这些数据集上的对比结果表明了基于表示的方法对于诸如多种光照、表型和遮挡等噪声情形更鲁棒。

(3)在这4个数据集上，所提出的方法显著优于PCA和LPP，表明在特征抽取中捕获数据局部结构和流行结构上的重要性。

5 结束语

本文提出了一种鲁棒的维度约简方法，与其它方法相比，通过将相似图学习和投影学习融入到一个联合优化框架，能够学习到全局最优的投影矩阵。此外，我们的方法通过在更紧凑的低维表征空间学习相似图，能够发现数据最本质的相似结构。更重要的是，通过行稀疏范数的引入，本方法能够在维度约简过程中选择最重要的特征，极大提高了对于噪声的鲁棒性。在多个数据集上的实验验证了所提出方法的有效性。