机场终端区空域的多条进离场程序优化

周 隽，谷升豪

(1.中国民航大学 中欧航空工程师学院，天津 300300；2.中国民航大学 中法联合空管应用数学研究中心，天津 300300)

0 引 言

机场终端区是最为复杂的空域之一，航班拥堵的情况在这一空域屡见不鲜。合理设计机场进离场程序能够有效提高终端区空域利用率。所需导航性能(required navigation performance，RNP)是一种新兴的导航规范，尤其适用于机场终端区这类对导航精度要求较高的空域[1]。当前绝大部分的进离场程序是根据机场地理位置和环境借助计算机辅助软件设计的[2-4]。设计方案的有效性大多取决于人员经验，在充分利用空域的层面仍有可提升空间。

路径规划类的算法可用于进离场程序优化设计[5,6]。根据不同的空间维度可将相关研究分为二维[7-9]与三维[10,11]。二维优化一般假设航空器处于最优的运行高度。Pierre等应用遗传算法计算最短航路，通过顺时针或逆时针转弯的方式规避由凸包所表示的障碍物区域[7]。冯国强等综合运用A*算法与蚁群算法对航路进行智能规划，以A*算法的导向性加快蚁群算法的收敛速度[8]。三维优化更符合实际应用的需求，但相关研究比较有限。Granberg等基于网格图对多条进场程序进行了整数规划建模，考虑了爬升及下降角度、平滑转弯等约束，并通过改变航向角来规避障碍物[10]。根据进离场程序数目又可分为单一程序优化[7-9]与多条程序优化[10,11]。多条程序优化的难点主要在于需要满足航路间最小安全间隔。比较常见的方法是依序逐条生成程序，将已经生成的程序作为后序程序的障碍物加以规避。Polishchuk基于RNP导航规范依序生成逐渐汇聚的进场程序[11]。综合来看，单一的二维航路优化复杂度较低，但是不够贴近实际情况；而多条的三维航路优化现有的研究成果较少，且在航路建模及障碍物与飞行冲突的规避方式上有待补充和改进。

综上，本文提出一种基于改进的分支定界法的多条三维进离场程序优化算法。在模型层面考虑了转弯半径、爬升角和下降角等航路实际特点；在冲突规避方式层面，除改变航向外，还提出了保持飞行高度这一方式，不但符合实际运行习惯，同时拓展了问题的解空间。最终生成的进离场程序满足RNP导航规范，可以为程序设计人员提供有效的决策支持。

1 数学模型及单一进离场程序的优化算法

1.1 障碍物与进离场程序建模

将机场终端区的障碍物(例如山区、禁飞区等)及其相应保护区建模为底面与水平面平行的三维圆柱体。令M∈N表示圆柱体总个数，每个圆柱体Ωj,j=1,…,M定义为(Cj(xj,yj),rj,zjinf,zjsup)，其中Cj(xj,yj)与rj分别表示Ωj两底面的圆心与半径，zjinf与zjsup分别表示下底面与上底面的高度。

令N∈N表示需要构建的进离场程序总个数。每个程序γi,i=1,…,N由两部分构成：水平平面内由一系列首尾相连且彼此相切的线段和圆弧构成的光滑曲线γiH，以及竖直平面内囊括此程序上航迹剖面的近似扇形区域γiV。在水平平面，曲线γiH连接起点Ai(xAi,yAi)与终点Bi(xBi,yBi)，定义为函数：γiV

γiH:[0,1]→R2

其中，γiH(0)=(xAi,yAi)，γiH(1)=(xBi,yBi)。在竖直平面，起点Ai对应的高度为HAi，近似扇形区域γiV定义为函数

1.2 数学模型

对于给定的进离场程序γi，每个障碍物对应的三维圆柱体Ωj与两个决策变量相关联：sij和tij。当γi与Ωj相接触并且用以下方式之一对Ωj进行规避：顺时针转弯、逆时针转弯、保持当前飞行高度，则此时Ωj对γi来说是“激活的”，以决策变量sij来表示

而tij则表示了γi对Ωj的规避方式

当所有决策变量(sij,tij)j=1,…M的取值确定，与之相对应的进离场程序γi的构型随之确定：按照圆心到该程序起始点连线的水平投影长度递增的顺序对障碍物进行排序，而后根据选取的障碍物规避方式构造航路。

航空器在机场终端区运行需要满足诸多约束条件，包括障碍物规避、对正跑道、最大最小转弯半径等约束，还需额外考虑航路之间的最小安全间隔约束(水平方向3海里，竖直方向1000英尺)，这对于保证航空器安全运行至关重要。具体实现方法见2.2，2.3。

于是，我和同行的诗友轮流驾驶，开始聊一些家长里短，之后又转移到工作的话题，直到太阳西沉，夜色吞没了大地和山峦的某个瞬间，车内才突然陷入了沉默。

单一进离场程序γi对应的加权长度Lγi定义为

(1)

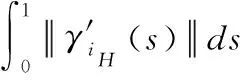
(2)

1.3 单一进离场程序的优化算法

由于数学模型中决策变量的取值为整数，进离场程序优化问题实际被建模为整数规划问题，应用分支定界法进行解算。其分支策略是基于障碍物规避方式提出的：对于程序γi,i=1,…,N，每一个障碍物Ωj,j=1,…,M可以分出4支，分别是：不激活(sij=0)、激活且以逆时针转弯规避(sij=1,tij=0)、激活且以顺时针转弯规避(sij=1,tij=1)、激活且以保持飞行高度规避(sij=1,tij=2)。设SP为求解进离场程序γi的分支界定法中生成的一解空间子集，其中只有部分决策变量的值确定，记作{(sij,tij)j∈J,J⊂{1,…,M。则SP的目标下界通过以下方式计算：将未取值的决策变量设为未激活，即{sij=0j∈(1,…,M)/J；构造相应的进离场程序，记作γiSP；根据式(1)计算其值LγiSP即为SP的目标下界。若LγiSP大于当前最优值，则对SP进行剪枝，进而逐步缩小搜索范围以获得最优解。

2 多条进离场程序的优化算法

对于每条新生成的航路，首先检测它是否与已生成航路发生冲突。若冲突存在，则可以通过顺时针转弯、逆时针转弯、保持飞行高度3种不同的方式在冲突区域附近对新生成的航路进行扰动，以改变其局部结构，进而规避冲突。

2.1 方法概述

应用依序策略逐条生成进离场程序，已经生成的程序成为新生成程序的障碍物。每条程序首先应用1.3中的分支定界法生成。随后，检测它是否与已生成航路发生冲突。若冲突存在，则对冲突区域进行聚类分组。将每组冲突按照1.1中的障碍物模型建模成三维圆柱体，称作“虚拟障碍物”。航路冲突的检测、聚类以及虚拟障碍物的生成方法见2.2。当不止一个虚拟障碍物存在，按照圆心到程序起始点连线的水平投影长度递增的顺序，对它们进行排序。为解决第一个虚拟障碍物所对应的航路冲突，在冲突区域附近对当前航路进行局部扰动。然后重新应用分支定界法构建剩余部分的航路，并再一次用相同方法对剩余部分航路进行冲突检测和解决。最终，按上述方法逐段生成进离场程序，其中每段程序均在分支定界法计算的最优解基础上进行局部扰动，进而保证最终解的优越性。航路冲突解决的算法见2.3。

2.2 航路冲突检测算法

考虑一对航路γi和γi′(i≠i′)，首先，在水平平面检测γiH和γi′H是否存在不满足3海里水平间隔的航路段；若存在，则针对这样的航路段继续在竖直平面检测是否满足1000英尺的竖直间隔。将同时不满足水平间隔和竖直间隔的航路段定义为冲突航路段。

2.2.1 水平平面冲突检测

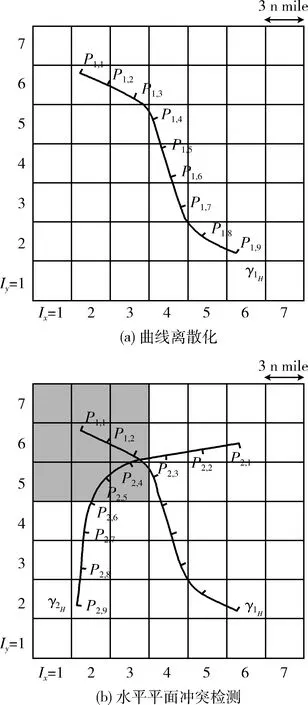
图1 水平平面冲突检测示例

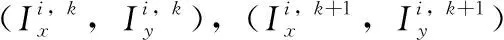
2.2.2 竖直平面冲突检测

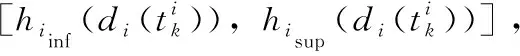
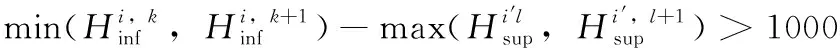
当两个航路段同时发生水平冲突和竖直冲突，则定义二者之间存在冲突。

2.2.3 虚拟障碍物的生成方法

将存在冲突航路段的单元格定义为冲突单元格。对于冲突单元格(Ix,Iy)定义其高度的下界和上界，分别记作Zinf(Ix,Iy)和Zsup(Ix,Iy)。令I⊂{1,…,N}表示已经生成的航路的编号集合，并且令{γik,k+1|k∈Ki,Ki⊂{0,…,Ni},i∈I}表示(Ix,Iy)单元格内，与当前航路存在冲突的航路段的集合，则

2.3 航路冲突解决算法

当生成了不止一个虚拟障碍物，则说明当前航路与已生成的航路存在多处冲突，此时在第一个虚拟障碍物Ωf(Cf(xf,yf),rf,zfinf,zfsup)对应的冲突区域附近对当前航路进行局部扰动。与2.2中类似地，设sij和tij是与Ωf相关的两个决策变量，提出3种规避Ωf的航路局部扰动方法：沿Ωf逆时针转弯(sij=1,tij=0)、沿Ωf顺时针转弯(sij=1,tij=1)、在Ωf底面处保持飞行高度zfinf(sij=1,tij=2)。考虑到保持飞行高度会增加油耗和污染气体的排放，因此优先考虑通过转弯的方式解决冲突：当顺、逆时针转弯均可以解决冲突时，取长度较短的作为新的解；当只有其中一种方式能够解决冲突时，直接将其设为新的解；当转弯无法有效解决冲突时，考虑保持飞行高度的方式；若3种方式均无法解决冲突，则选择剩余冲突最少的为新解。具体航路局部扰动方式见2.3.1，2.3.2。

2.3.1 通过转弯实现的局部扰动

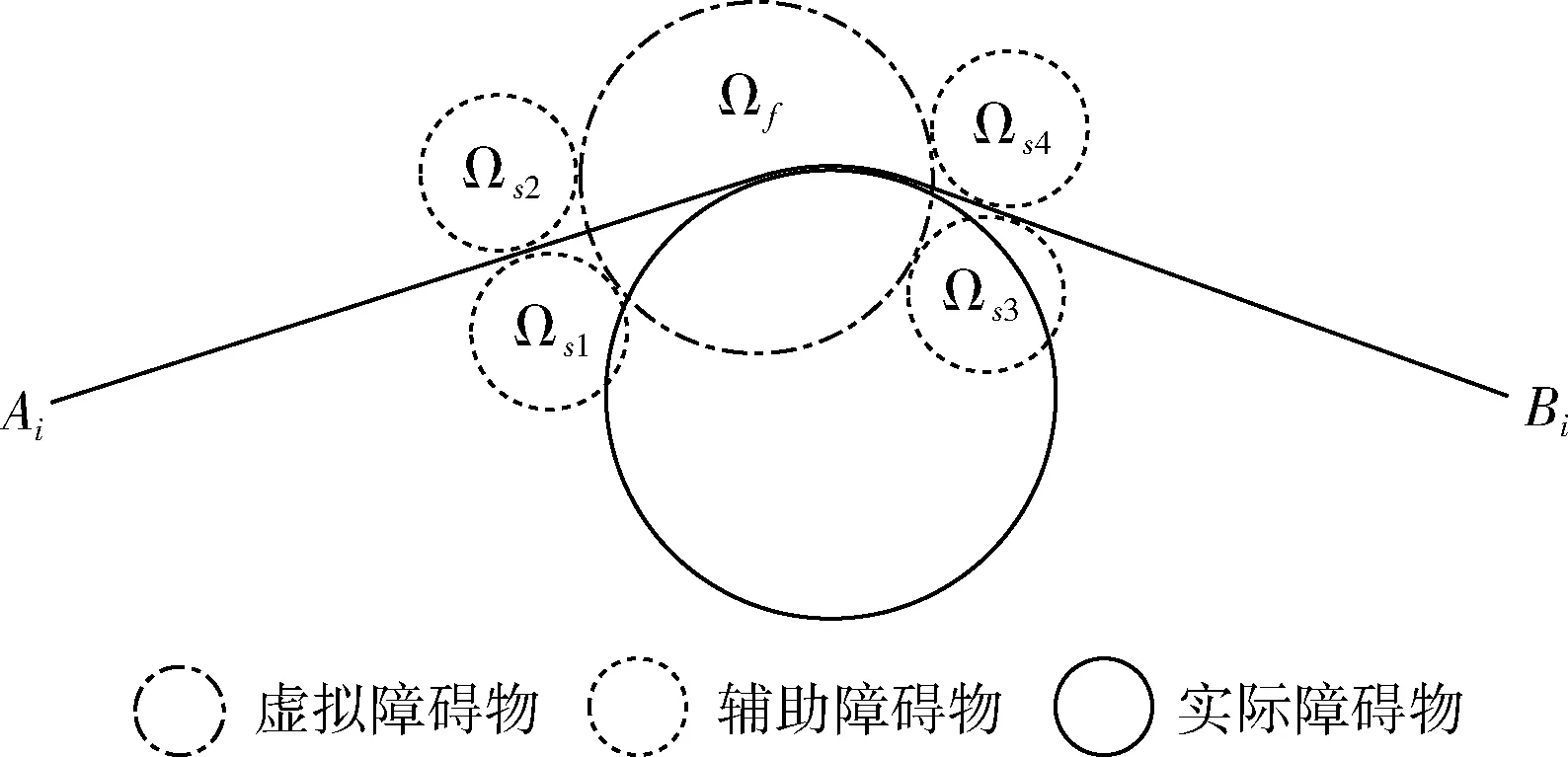
图3 虚拟障碍物和辅助障碍物

2.3.2 通过保持飞行高度实现的局部扰动

图4 通过转弯方式局部扰动航路

图5 通过保持飞行高度方式局部扰动航路

2.3.3 航路后处理方法

通过转弯方式进行局部扰动的航路在冲突区域附近的构型由3个连续且两两相切的圆弧段组成，这种构型方式符合RNP的运行规范[5]。但在实际运行中，飞行员在转弯规避冲突后，往往直接飞向下一导航点。因此，对已经生成的航路进行后处理。对于进场程序(或离场程序)，每一次通过转弯进行的局部扰动，将虚拟障碍物之前(或之后)的辅助障碍物设为未激活，重构航路。若重构的没有与其它航路产生新的冲突，则接受此重构航路作为新的解。

3 算例仿真

为测试算法的解算能力及运算效率，给出两种不同的人为生成的算例。取目标函数(式(1))中惩罚系数c1=1、c2=0；取进场程序最大、最小下降角度分别为2.4°和0.92°；离场程序最大、最小爬升角度分别为6.3°和4°。所有测试均在2.4 GHz处理器，8 GB安装内存的Linux平台上运行。由于篇幅限制，每个算例中进离场程序的起点终点坐标，以及障碍物的相关参数取值参见链接https://pan.baidu.com/s/1l-U_-ZrLzgXzBcvnweq2Ew(提取码：b3za)。

3.1 算例1

本算例考虑的是1条进场程序、1条离场程序及6个障碍物。应用分支定界法单独生成进离场程序，并应用2.2中算法进行冲突检测，航路构型及冲突区域如图6所示。图6(a)中深灰色阴影圆盘表示为使进离场程序对正跑道而人为设置的辅助障碍物，黑色圆圈表示实际障碍物；图6(a)、图6(b)中的浅灰色区域表示进离场程序的初始冲突区域。应用2.3中算法解决航路冲突，进行两次测试，测试1优先生成离场程序(仿真结果如图7(a)、图7(c)、图7(e)，测试2优先生成进场程序(仿真结果如图7(b)、图7(d)、图7(f)。数值结果见表1。每个测试耗时约为0.5 s。两个测试均可以解决航路间的冲突。

测试1中通过生成包裹冲突区域的虚拟障碍物及相应辅助障碍物(图7(c)中虚线圆圈)，并且令进场程序沿此虚拟障碍物逆时针转弯，可以有效解决航路间冲突。随后应用2.3.3中方法对获得的进场程序进行后处理以减少不必要的转弯(如图7(c)所示)。另外，由图7(e)可见，局部扰动后的进场程序此时在离场程序的下方通过，有效地规避了原有的冲突。类似地，测试2中对离场程序进行局部扰动，使得航路长度边长，相应的竖直平面内飞行高度增加，因此进场程序可以从下方通过，规避了原有的冲突(如图7(f)所示)。通过比较两个测试的数值结果可见，测试2的航路总长度更短，这说明改变航路生成顺序对解的质量有一定影响。

图6 算例1原始进离场程序及冲突区域

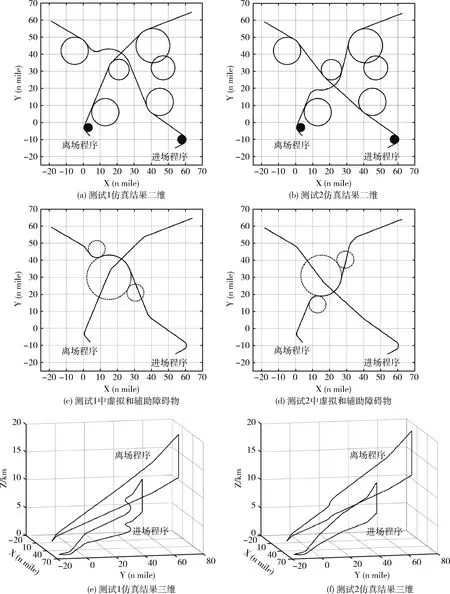
图7 算例1仿真结果

表1 算例1数值结果

3.2 算例2

本算例考虑的是2条离场程序(图8(a)中的γ1，γ2)、3条进场程序(图8(a)中的γ3，γ4，γ5)及9个障碍物。应用分支定界法单独生成的进离场程序及原始冲突区域如图8所示。图中辅助障碍物、实际障碍物与初始冲突区域的表示方法与图6相同。应用冲突解决算法的仿真结果如图9所示。进离场程序按标号递增的顺序逐一生成。其中γ2以顺时针转弯的方式规避它与γ1的冲突；γ3与γ1、γ2均无冲突，因此无需调整；γ4以保持飞行高度的方式规避与γ1的冲突，保持飞行高度航段如图9(a)虚线部分所示，航路构型的剖面图如图9(c)所示；γ5分别以顺时针、逆时针转弯的方式规避它与γ2、γ3的冲突。所有虚拟与辅助障碍物如图9(b)所示。最终所有冲突得以解决。数值结果见表2。测试耗时约为1.1 s。

图8 算例2原始进离场程序及冲突区域

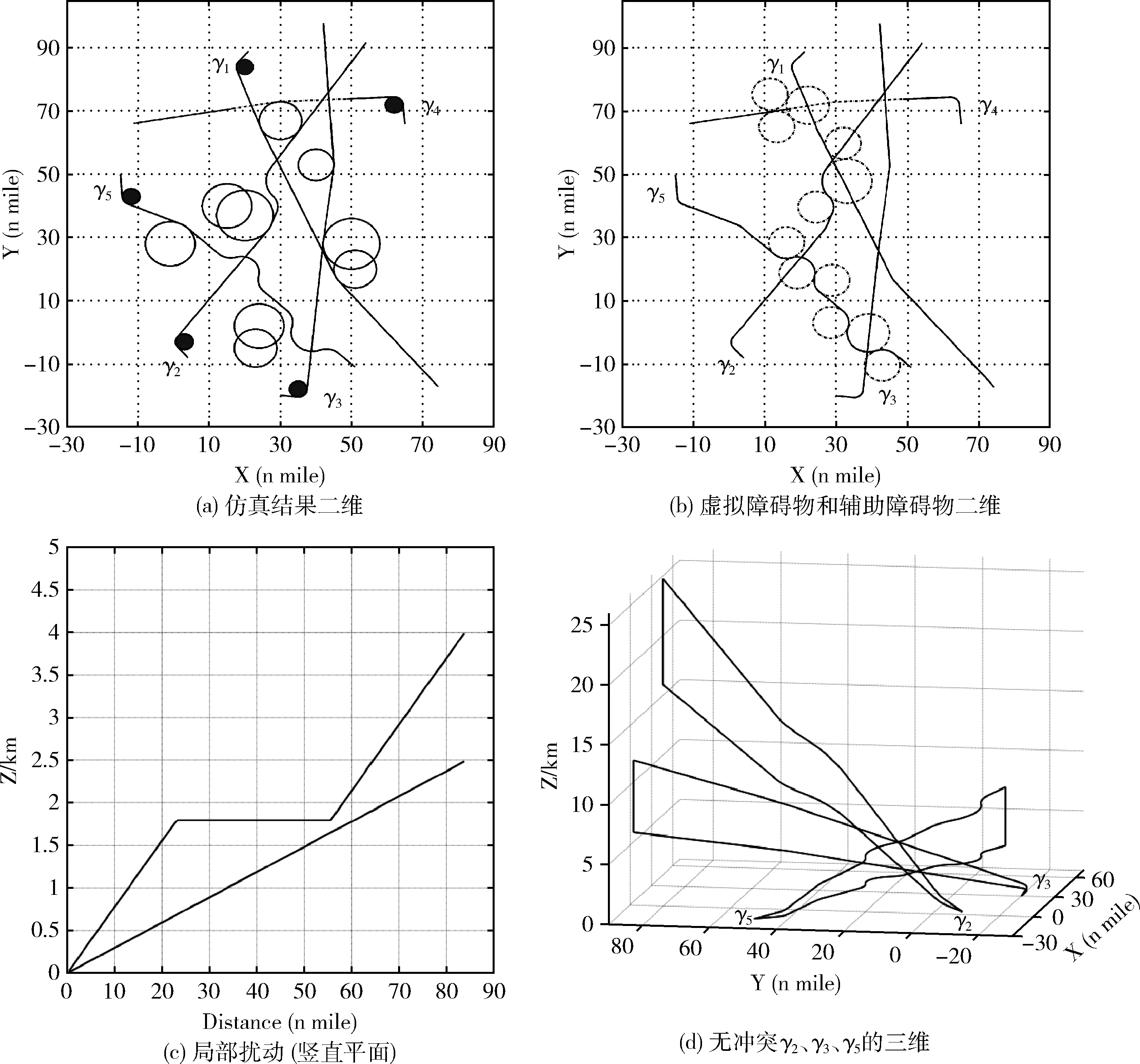
图9 算例2仿真结果

表2 算例2数值结果

4 结束语

本文结合机场周边环境、空域限制因素，提出了机场终端区空域多条进离场程序的优化设计算法。首先，对进离场程序及障碍物进行了三维建模，模型符合RNP导航规范。其次，开发了适用于三维模型的冲突检测及冲突解决算法。对于存在冲突的程序给出顺、逆时针转弯、保持飞行高度3种不同的冲突解决策略，符合空管和飞行员的日常操作习惯。算法基于经典的分支定界法进行改进，以保证最终解的优越性。仿真结果表明，在复杂障碍物布局下，算法能够高效地解算出多条无冲突且符合RNP规范的进离场程序，可以为实际进离场程序设计提供有效的决策支持。