地锚式独塔单跨空间双缆面悬索桥结构体系分析

赵 煜，李畅畅，吴领领，周勇军*，丁伟慧

(1.长安大学公路学院,西安 710064; 2.旧桥检测与加固交通行业重点实验室,西安 710064)

新颖桥梁结构体系,一直是桥梁工作者研究的热点。悬索桥结构轻盈,造型优美,是桥梁的主要备选之一。悬索桥不同结构体系下的受力行为也成为近几年来的研究重点。

陈策等[1]利用有限元模型对泰州长江公路大桥矢跨比等体系参数对其结构行为的影响进行了研究。唐茂林等[2]比较了西堠门大桥矢跨比在1/8～1/15变化的结构受力情况。蒋望等[3]分析了某悬索桥矢跨比等对构件用量和结构受力、变形的影响,给出了适用范围。柴生波等[4-6]利用理论推导及有限元计算对双缆悬索桥体系的力学特性进行了研究,给出了求解方法。肖汝诚等[7]将两种双塔三跨缆索承重桥进行分析对比,探讨在不同跨径内结构体系的优选。陶庆东等[8]以吉林某两种不同体系自锚式悬索桥为实例,分析了自振特性,并研究了地震作用下的稳定性。江南等[9]利用某悬索桥建立矢跨比为1/15～1/5的有限元计算模型,研究得到并合理解释了结构刚度随矢跨比的真实变化规律。罗世东等[10]以某海湾双塔三跨悬索桥的可行性研究为背景,研究了主要设计参数对结构体系的影响规律,并分析了悬索桥受力特点对主缆矢跨比、等参数变化的敏感程度。周轶等[11]模拟悬索单元时采用线性单元和非线性单元,从而得到相应的刚度矩阵及质量矩阵,进而计算得到悬索在面内的自振频率。周云岗等[12]采用ANSYS对主跨 1 400 m 的三种缆索体系桥考虑几何非线性,分析了主梁的最大挠度等对矢跨比等参数的敏感程度,给出了主要构件刚度取值范围。段瑞芳等[13]采用MathCAD编制了主缆分析程序,分析了主缆弹性模量等因素对无应力长度的影响,并研究了各参数对空缆状态与索鞍预偏量的影响。何婧[14]通过有限元分析,研究了大跨度双缆悬索桥结构体系及其受力特性。周建庭等[15]提出通过有限点监测的悬索桥位移获取技术和桥梁安全评估技术。侯康[16]对多塔悬索桥塔梁连接形式、缆梁连接形式等结构体系参数进行了研究,并提出了合理适用范围。郑州[17]对湖南昭华湘江大桥矢跨比进行单因素参数分析,总结了在成桥状态下,采用不同的矢跨比,桥塔、主梁等构件的内力变化规律。陈彦江等[18]采用一致激励工况研究得到黏滞阻尼器对独塔自锚式悬索桥提供了一定的阻尼。杜斌等[19-20]以贵州省马岭河3号特大桥为研究对象,对影响公轨两用悬索桥线形控制的参数进行敏感性分析,并研究了某独塔自锚式悬索桥的静动力特性及设计参数影响程度。田浩等[21]设计了主缆室外温湿度监测试验,研究了大跨悬索桥西堠门大桥主缆温湿度长期监测与分布规律。

中国对地锚式独塔单跨空间双缆面悬索桥的合理结构参数研究较少,本文将通过对某地锚式独塔单跨空间双缆面悬索桥的主缆垂跨比、边跨锚固角度、主梁截面形式等主要结构参数对结构受力行为影响的研究,确定其合理参数分布,为该类桥梁设计时相关参数的拟定提供参考。

1 工程概况

某地锚式独塔单跨悬索桥,采用空间双缆面,主缆垂跨比布置为1/15,背索锚固点距桥塔70 m,锚固角度60°。桥梁整体纤薄,线性流畅,整体色彩简洁大气,该桥效果如图1所示。吊杆间距布置为12.5 m+24 × 10 m+12.5 m,共记25根。该桥主要参数拟定为:桥长265 m,桥梁标准断面宽18 m,塔高118 m,主缆最高点至塔顶10 m,桥台采用扩大基础。该桥桥塔结构采用C50混凝土,主梁采用Q345d钢材。图2为桥梁总体布置图。

图1 桥梁结构效果图Fig.1 Bridge structure rendering

图2 桥梁结构总体布置图Fig.2 Overall layout of bridge structure

2 计算模型

2.1 模型建立

采用有限元软件Midas Civil对该地锚式独塔单跨悬索桥进行三维建模分析。主梁用梁单元模拟,研究中采用π型钢梁与钢桁梁两种不同的主梁截面形式,分别采用“单梁法”和“梁格法”进行建模,主梁梁端的支座通过弹性连接模拟,主梁形心与吊杆锚固采用主从约束模拟,模拟吊杆在主梁上的锚固。考虑到地锚式悬索桥的几何非线性影响,根据各个桥梁构件的形式和受力特点,桥塔、桥墩均采用梁单元进行模拟,主缆、吊索采用索单元模拟。主缆、吊索的截面参数如表1所示。

表1 吊索、主缆截面参数

按照以上方法建立空间模型,主梁为π型钢梁的全桥模型共划分节点153个,单元141个,其中梁单元37个,索单元104个；主梁为钢桁梁的全桥模型共划分节点871个,单元2 052个,其中梁单元1 740 个,索单元104个,板单元208个。全桥结构计算消隐模型如图3所示。

图3 全桥消隐模型示意图Fig.3 Schematic diagram of the full bridge blanking model

2.2 计算荷载

根据工程实际特点,对桥梁结构进行体系分析计算时所采用的荷载工况如下：

(1)结构自重:结构自重软件自动计算。

(2)二期恒载:沥青混凝土容重24.0 kN/m3,栏杆重量2.5 kN/m。

(3)基础变位:本桥为超静定结构,主塔塔底20 mm 基础变位。

(4)移动荷载:人群荷载2.5 kN/m2,汽车荷载公路-I级。

(5)整体升温:升温荷载按现行规范取29 ℃。

2.3 研究参数的确定

对于该地锚式独塔单跨悬索桥,在跨径一定的情况下,合理的主缆垂跨比、边跨锚固角度可改善结构整体受力,尤其是加劲梁受力,降低加劲梁造价；同时,悬索桥的加劲梁支承在柔性的主缆上,提供了较大部分的恒载,对结构的重力刚度影响较大,选用合理的加劲梁形式将直接影响结构的成桥平衡状态。因此,根据全桥的构造特点和总体布置方案,综合考虑各种因素后,选取结构体系研究参数见表2,主要对结构各参数下恒活载、升温荷载下主缆、吊杆受力及主梁受力变形情况进行研究。

3 结构体系参数

3.1 主缆垂跨比

主缆垂跨比的不同会造成结构在成桥状态下主缆和吊杆受力的不同,加劲梁的受力也会随之改变。图4、图5分别为恒载效应下的主缆、吊杆受力对比图以及主梁弯矩对比图。由图4、图5可知,随着垂跨比的增大,主缆力、主缆背索力均逐渐减小。边吊杆与中吊杆的受力差异较大,且垂跨比的改变对边吊杆受力的影响较大,对远离边吊杆的吊杆受力影响较小。随着垂跨比的增大,主梁的弯矩逐渐减小。由于吊杆的“多点弹性支承”作用,主梁弯矩分布较为均匀。

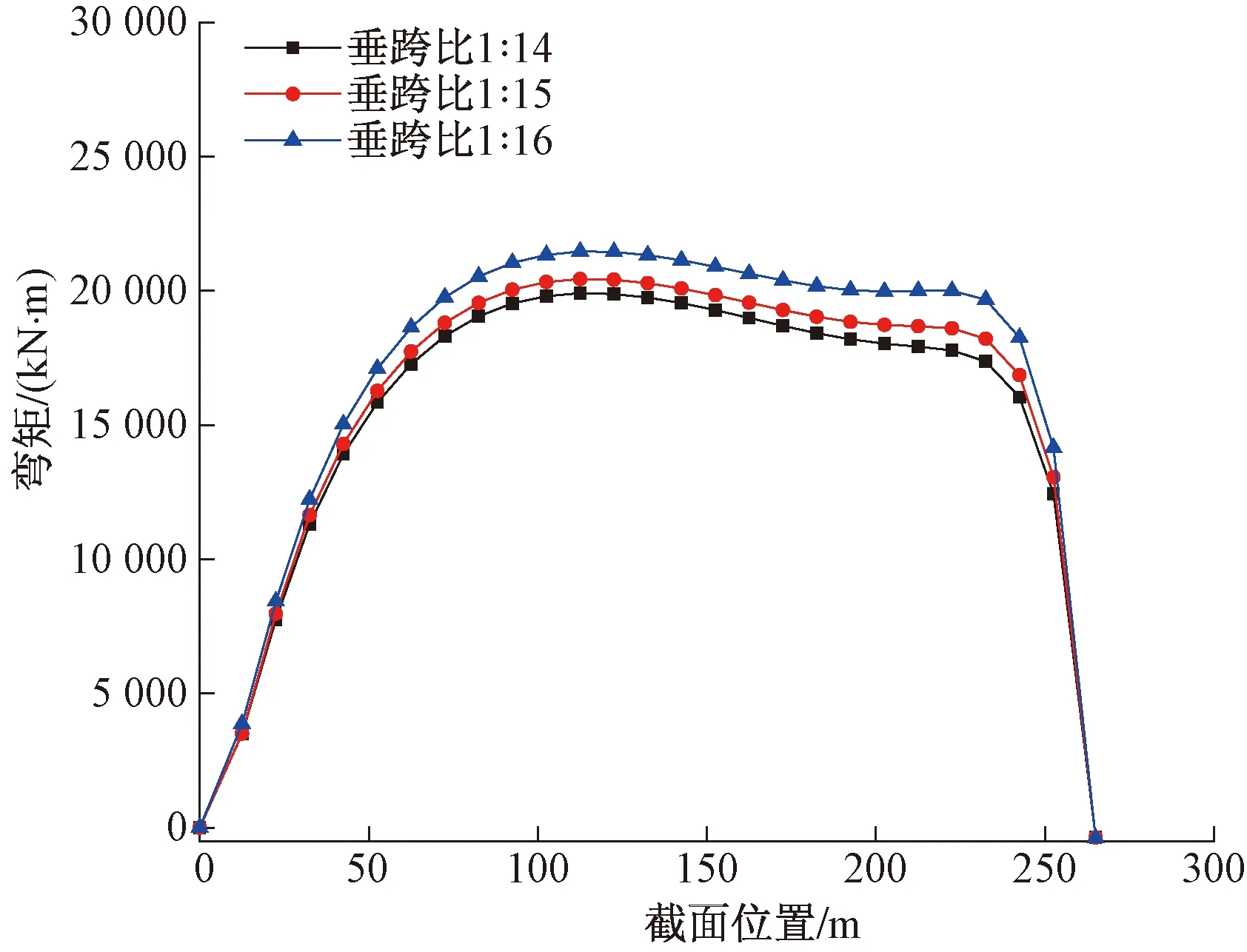
图5 不同垂跨比恒载效应下主梁弯矩对比图Fig.5 Comparison of bending moments of main beam under dead load of different rise-span ratios

在移动荷载等可变荷载效应作用下,结构的整体平衡状态仍需满足要求。通过对结构在设计活载作用下的分析,可以得到在不同垂跨比下主梁的弯矩和挠度包络图如图6所示。分析可知,在活载作用下,最大弯矩及最大挠度发生在1/4跨和3/4跨；随着垂跨比的增大,主梁弯矩及挠度均呈减小趋势。

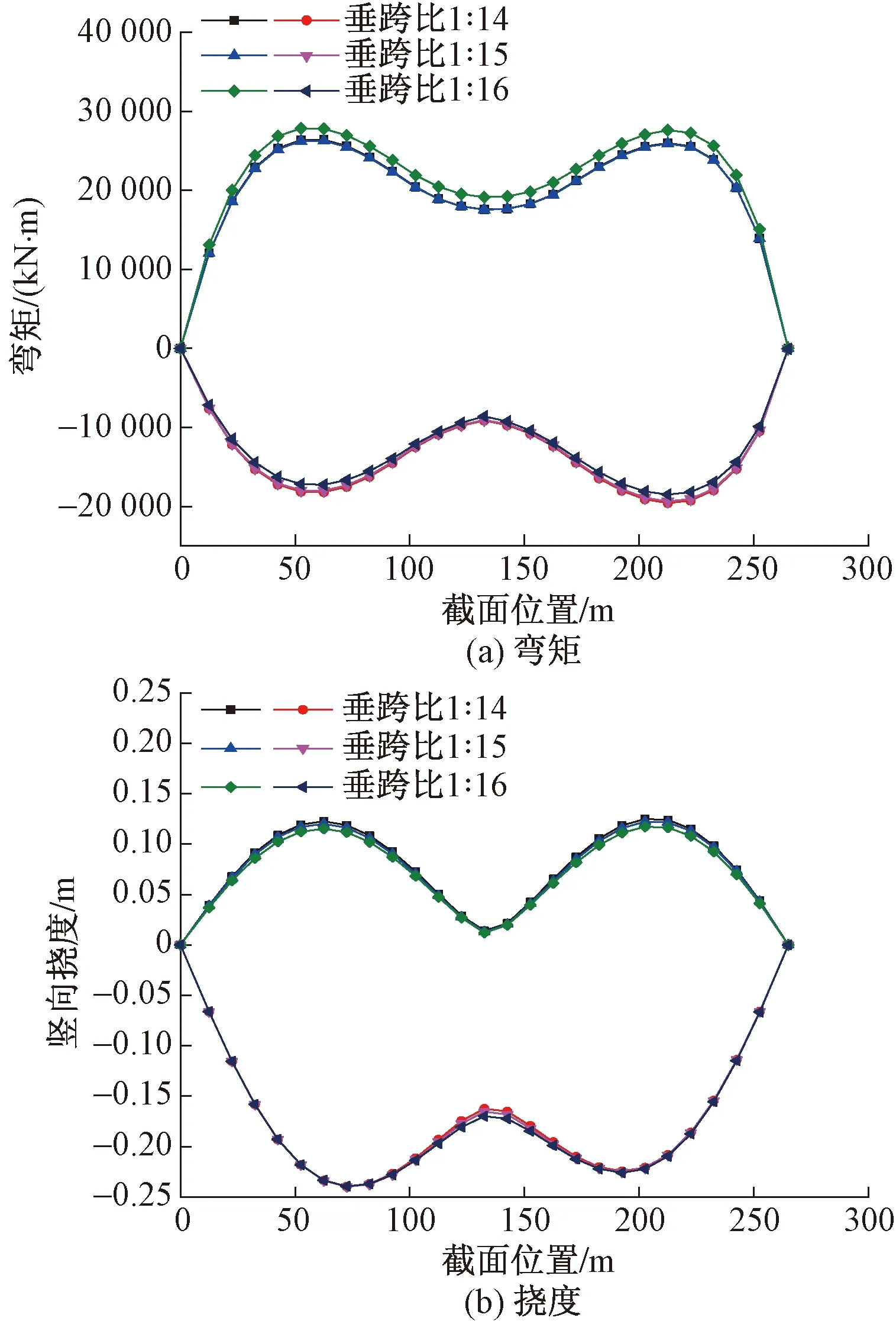
图6 不同垂跨比活载效应下主梁弯矩、挠度包络图Fig.6 Bending moment and deflection envelope of main beam under live load of different rise-span ratios

不同的主缆垂跨比引起了主缆受力的差异,且由于该桥为独塔结构,桥塔左右结构不对称,主缆力和主缆背索力对塔底将产生不平衡弯矩。对结构施加车道荷载并改变集中力的作用位置,可以得到不同垂跨比活载作用下的塔底弯矩对比,如图7所示。在同一种荷载作用位置下,随着垂跨比的增大,桥塔塔底弯矩逐渐减小；在不同荷载作用位置下,当荷载作用于跨中时桥塔塔底产生的弯矩最大。

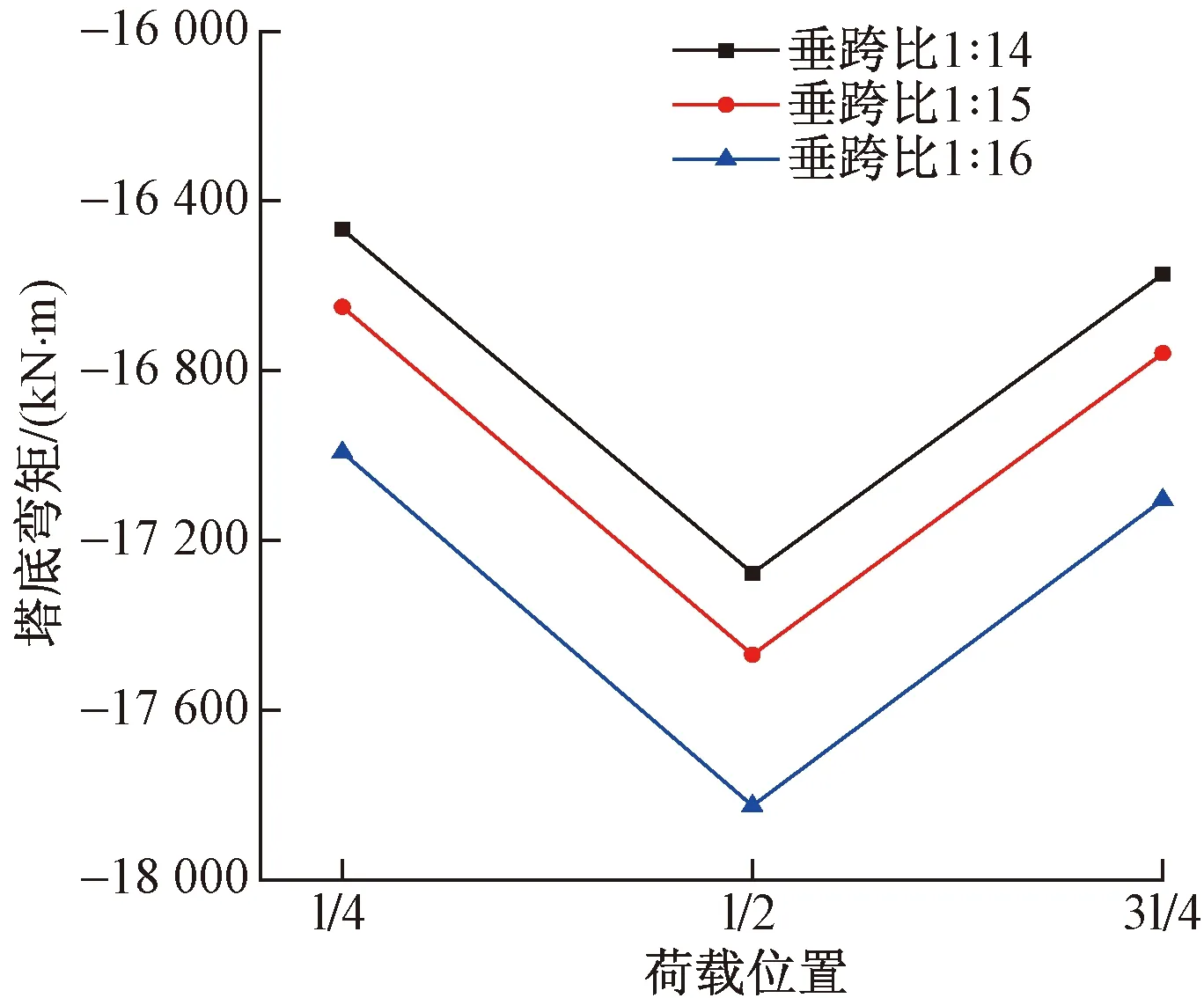
图7 不同垂跨比活载效应下塔底弯矩对比Fig.7 Comparison of bending moments of tower bottom under live load of different rise-span ratios

温度对结构的受力影响较大,该工程的环境温度变化较大,通过对结构进行温度影响分析,可以得到在不同垂跨比下,结构的温度效应对比如图8所示。在温度荷载作用下,最大挠度发生在跨中位置；随着垂跨比的增大,主梁因温度作用产生的弯矩与挠度呈减小趋势。

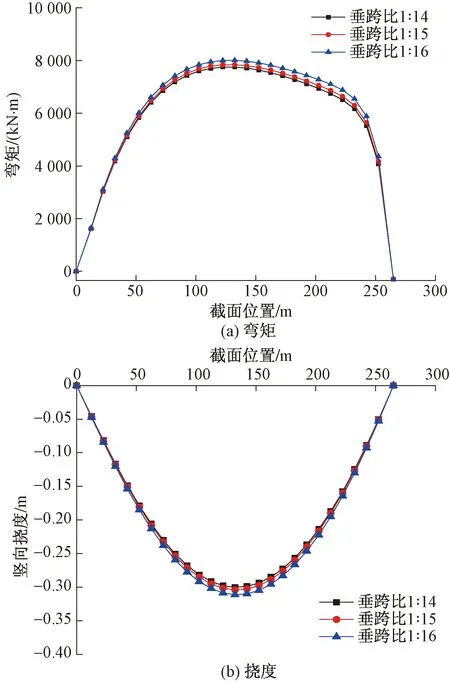
图8 不同垂跨比升温荷载下主梁弯矩、挠度对比Fig.8 Comparison of bending moment and deflection of main beam under heating load of different rise-span ratios

3.2 边跨主缆锚固角度

边跨不同的主缆锚固角度对主缆的受力有影响,对边跨主缆的锚固角度设置45°、60°、75°锚固形式,具体表现如图9所示。

图9 边跨不同锚固形式示意图Fig.9 Schematic diagram of different anchoring forms

不同主缆锚固角度下的主缆受力及吊杆受力对比如图10所示。分析可得,相对于背索而言,锚固角度的不同,对主缆受力的影响不明显,但对主缆背索力影响较为明显,且随着锚固角度的增大,主缆背索力减小。锚固角度的改变,对靠近改变锚固角度端的吊杆受力影响较大,对远处的吊杆受力影响不明显。不同边跨锚固角度下的主梁主要截面的弯矩效应对比如图11所示,随着锚固角度的增大,主梁的弯矩随之减小,同理,由于吊杆的“多点弹性支承作用”,主梁的弯矩分布较为均匀。

图10 不同锚固形式恒载效应下主缆、吊杆受力对比Fig.10 Comparison of the force of the main cable and the boom under dead load of different anchoring forms

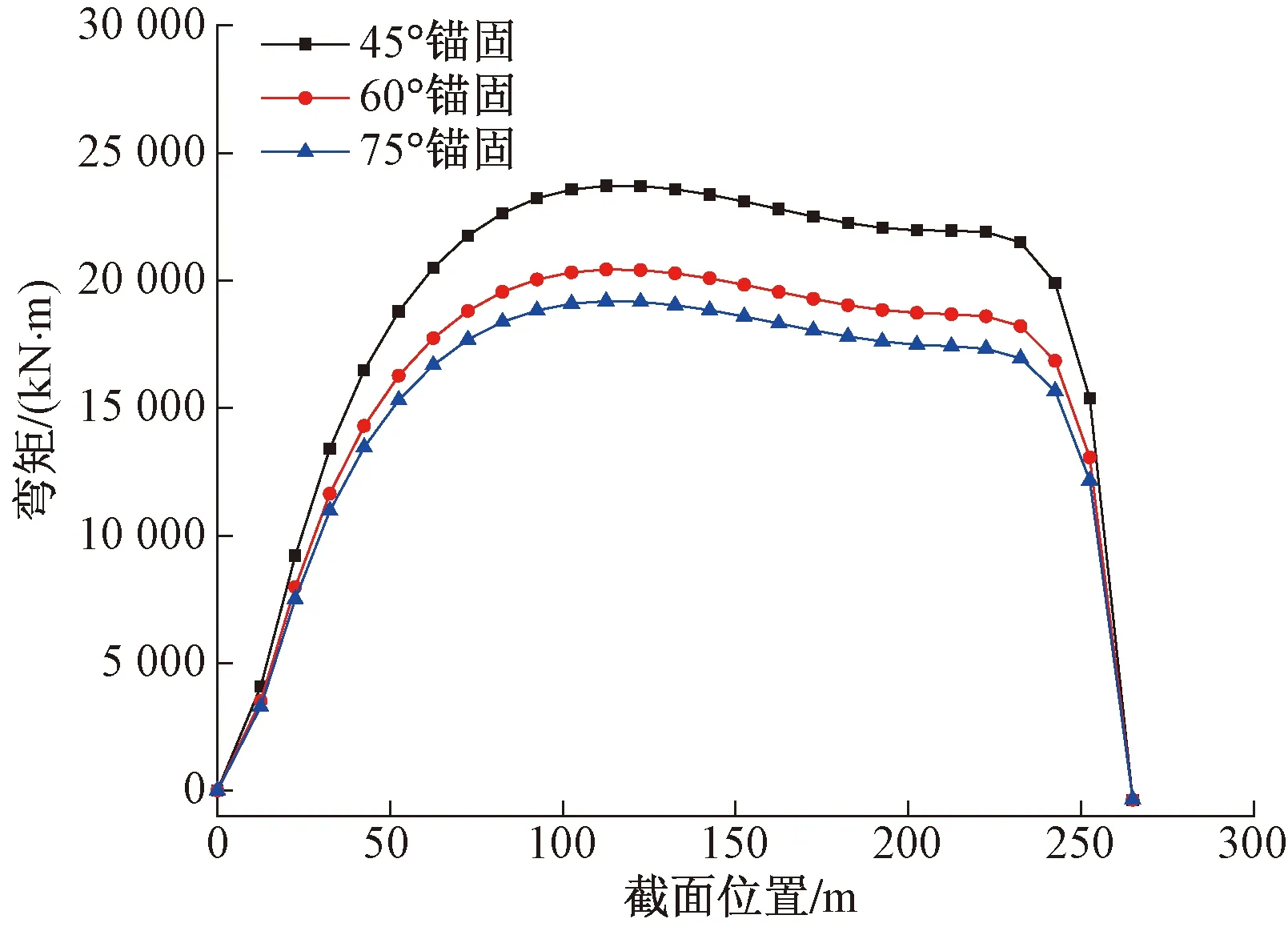
图11 不同锚固形式恒载效应下主梁弯矩对比Fig.11 Comparison of bending moments of main beam under dead load of different anchoring forms

通过对结构在设计活载作用下的效应计算,可以得到在不同锚固角度下主梁的弯矩包络图和挠度包络图如图12所示。活载作用下,最大弯矩及最大挠度发生在1/4跨和3/4跨；随着锚固角度的增大,主梁弯矩及挠度均呈减小趋势。

不同锚固角度会引起主缆受力的差异,主缆力和主缆背索力对塔底将产生不平衡弯矩。对结构施加车道荷载并改变集中力的作用位置,可以得到不同锚固角度活载作用下的桥塔结构塔底弯矩对比如图13所示。在同一种荷载作用位置下,随着锚固角度的增大,桥塔塔底弯矩逐渐减小；在不同荷载作用位置下,当荷载作用于跨中时桥塔塔底产生的弯矩最大,且锚固角度的增大能减小这种差异。

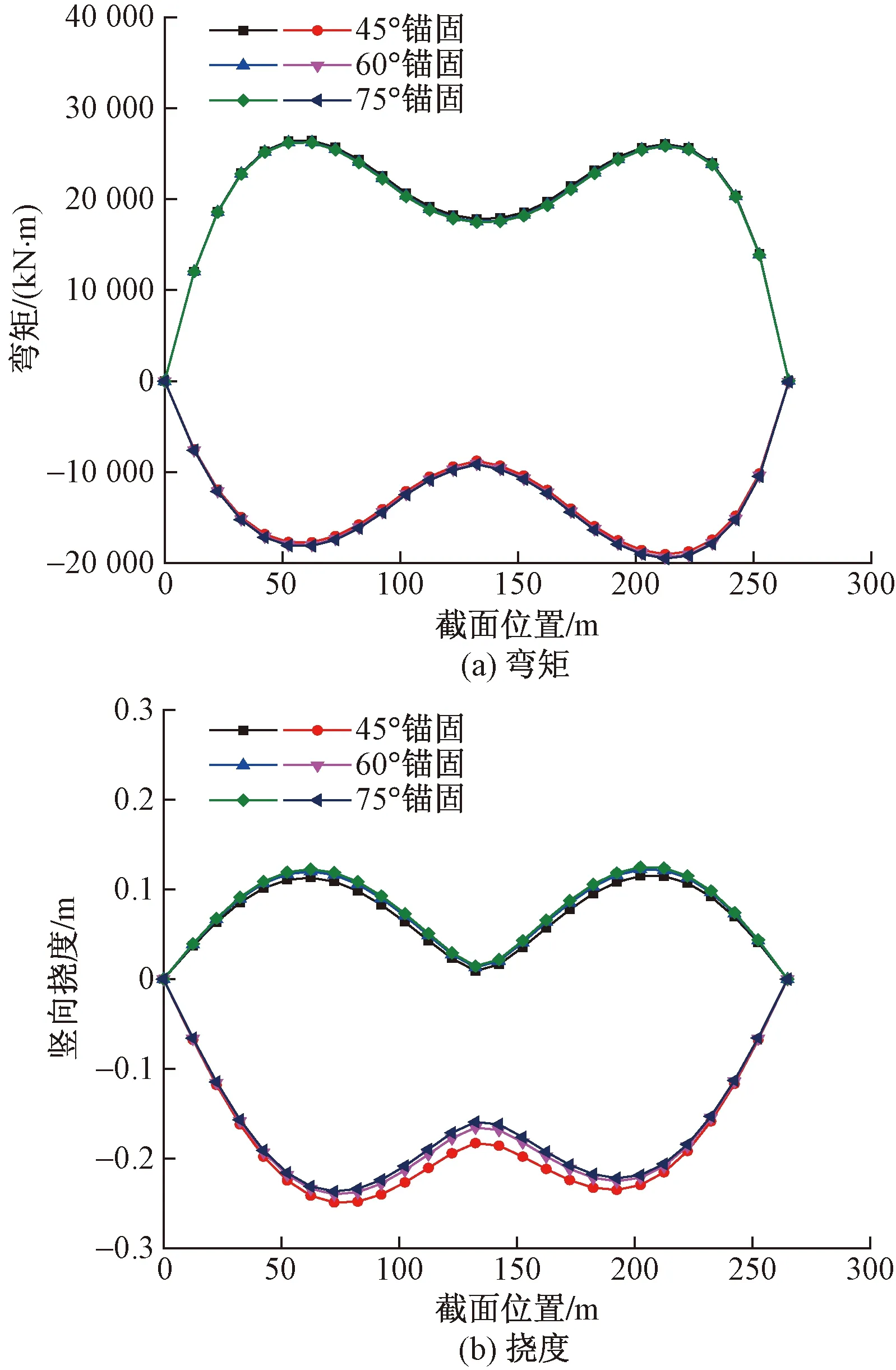
图12 不同锚固形式活载效应下主梁弯矩、挠度包络图Fig.12 Bending moment and deflection envelope diagram of main beam under live load of different anchoring forms

图13 不同锚固形式活载作用下塔底弯矩图Fig.13 Bending moment diagram of tower bottom under live load of different anchoring forms

主梁在升温荷载效应下,弯矩、挠度对比如图14所示。在温度荷载作用下,最大挠度发生在跨中位置；随着锚固角度的增大,主梁因温度作用产生的弯矩与挠度呈增大趋势。

图14 不同锚固形式升温荷载下主梁弯矩、挠度对比Fig.14 Comparison of bending moment and deflection of main beam under heating load of different anchoring forms

3.3 加劲梁截面形式

图15 不同主梁形式恒载效应下主缆、吊杆受力对比Fig.15 Comparison of the force of the main cable and hanger under dead load of different main beam forms

选取π型钢梁、钢桁梁两种加劲梁截面形式对结构的分析,得到不同主梁形式下的恒载效应下主缆受力及吊杆受力对比如图15所示。采用的钢桁梁截面形式所引起的主缆受力及吊杆受力普遍比采用π型钢梁截面形式的大,原因是钢桁梁的自重较π型钢梁的自重较大,结构的重力刚度较大。

活载对结构的影响程度与结构的重力刚度大小密切相关。而桥梁结构的刚度一般以活载作用下桥梁挠度来衡量。通过对结构在设计活载作用下的效应分析,得到主梁形式活载效应下结构挠度包络图如图16所示。在活载作用下,钢桁梁截面形式下的活载引起的挠度比π型钢梁的明显较小,因在分析中钢桁梁结构形式的重力刚度较π型钢梁的大,故活载效应下钢桁梁的挠度较π型钢梁的小。

通过对结构进行温度影响分析,得到在主梁形式下,主梁的温度效应对比如图17所示。在温度荷载作用下,最大挠度发生在跨中位置；由于π型钢梁与钢桁梁所形成的结构刚度不同,且在本次分析中钢桁梁结构的刚度较π型钢梁的大,所以在荷载作用下钢桁梁结构产生的挠度较π型钢梁的小。

图16 不同主梁形式活载效应下主梁挠度包络图Fig.16 Deflection envelope diagram of main beam under live load of different main beam forms

图17 不同主梁形式升温荷载下主梁挠度对比Fig.17 Comparison of deflection of main beam under heating load of different main beam forms

4 结论

通过对地锚式独塔单跨空间双缆面悬索桥结构体系分析在主缆垂跨比、边跨主缆锚固角度、加劲梁截面形式等方面进行了的深入研究,可得到以下主要结论。

(1)增加和减小主缆的垂跨比,对主缆受力及主梁的内力和挠度影响较大,对中吊杆受力影响不明显,边吊杆影响较大。在所取恒载、活载等荷载工况下,随着垂跨比的增大,主缆受力逐渐减小,主梁的弯矩及挠度随之减小,塔底弯矩也随之减小。

(2)增加和减小背索的锚固角度,相对于背索而言,对主缆力的影响不明显,但对主缆背索力影响较为明显,且随着锚固角度的增大,主缆背索力减小；对靠近改变锚固角度端的吊杆受力影响较大,对远处的吊杆受力影响不明显。在所取恒载、活载和等荷载工况下,随着锚固角度的增大,主梁的弯矩及挠度随之减小,塔底弯矩也随之减小。

(3)增加钢桁梁的主梁截面形式,对主缆受力、吊杆受力及主梁的挠度影响较大。在所取恒载、活载等荷载工况下,钢桁梁截面形式主梁的结构所产生的主缆受力及吊杆受力较π型钢梁的大；主梁挠度较π型钢梁的小。