基于平行黏结模型的类岩石材料宏细观参数影响
2020-09-04刘远明
王 唯, 刘远明
(贵州大学土木工程学院,贵阳 550025)
由于工程岩体内部有原生裂纹的存在,压剪应力作用使得新生裂纹不断产生,岩石内部逐渐损伤弱化,最终原生裂纹与新生裂纹形成宏观裂缝。研究岩石裂纹的扩展对岩体工程施工与防灾减灾工程有非常重大的意义[1]。由于现场试验中无法观测岩石微裂纹的发育、扩展与贯通。基于颗粒离散元法将岩石离散成细观颗粒,并赋予颗粒之间接触模型,通过数值模拟手段监测岩石裂纹的生成。但是,岩石材料的宏观力学性质与细观参数并不一一对应,细观参数种类繁多相互之间交错影响,因此参数合理标定能响应宏观力学性质是岩土工程的重点和难点。
国外学者[2-4]对参数标定研究进行大量数值试验,建立了细观参数与宏观力学性质之间的关系。颜敬等[5]对无黏结颗粒材料设计正交试验研究了宏细观参数的关系;陈亚东等[6]通过三维颗粒流仿真试验,利用土体内摩擦角与静止土压力的关联,标定了砂土颗粒间的摩擦系数;刘富有等[7]用单轴压缩和巴西劈裂试验对灰岩的细观参数进行标定,牛林新等[8]采用多因素方差分析宏细观参数之间的影响,以单轴压缩实验匹配参数;赵国彦等[9]、丛宇等[10]研究了平行黏结模型的细观参数对宏观变形参数的影响;田世雄等[11]通过引入clump单元建立卵石颗粒,使其增大颗粒之间的咬合作用,分析了不同粗粒含量对土石混合体的力学性能影响。
综上所述,响应岩土材料的宏观力学特性值得深入研究。较多研究成果偏重于砂土无黏性材料,较少的黏结材料主要进行定性分析以及单轴抗压强度参数的匹配。因此基于离散元方法尝试设计正交试验,期望得到宏细观参数定量的表达式,同时结合室内常规三轴压缩实验、巴西圆盘劈裂试验为细观参数的选取进行验证,不仅为模拟岩石类材料细观参数提供参考借鉴,也为后续模拟非贯通节理直剪试验提供可靠依据。
1 实验方案
1.1 数值模拟
数值模拟试验通过计算机建模计算,能全面再现试样受力产生的力学行为,具有经济,可重复性强等特点。为能较好吻合岩石类材料的力学性质,赋予颗粒之间平行黏结接触模型。如图1所示为圆柱体试件,直径为50 mm,高度为100 mm。通过建立墙体来设定边界,预先设定最小颗粒半径Rmin=0.35 mm,最大半径Rmax=0.58 mm,在此半径范围内随机生成颗粒。

图1 建立数值模型Fig.1 Generate numerical model
选定岩石单轴抗压强度50%处为弹性阶段,以此求得弹性模量E和泊松比μ。岩石抗拉强度由σt=2P/πDh求出。剪切强度参数c、φ通过双轴试验设置不同围压σ3求得峰值应力σ1,以峰值应力σ1为纵坐标、围压σ3为横坐标,绘点拟合出最佳关系曲线并通过式(1)求出。宏观参数以相同方法求得。

(1)
式(1)中:m为拟合曲线斜率;σc为拟合曲线在纵坐标上的截距。
1.2 室内试验
材料选用海螺牌32.5R快硬硅酸盐水泥和贵阳市某砂场细砂,质量比为砂子∶水泥∶水=3∶2∶1。预先制作200 mm的立方体再钻芯取样,根据工程岩体试样方法标准[12]人工打磨成直径50 mm、高度100 mm的圆柱体,如图2所示。试验设备选用中科院武汉岩土力学研究所自行研发的RMT-301岩石与混凝土伺服压力机。试验过程中,将试样转入三轴压力盒中,先达到预设围压,伺服稳定控制围压,再以0.005 mm/s的速度施加轴向压力。

图2 试验试件Fig.2 Experiment sample
2 宏细观参数影响研究

2.1 正交试验设计

根据上述假设以宏观力学性质作为正交试验的衡量指标,挑选因素进行表头设计,由于部分因素的影响规律呈非线性,将每种因素细分为7水平,再根据正交原理设计。正交试验设计如表1所示,正交矩阵序列如表2所示。从表2可看出大部分宏观参数符合多数微风化岩石的力学参数范围内,单一对比各项指标可发现存在一些偏差,例如第23组数据不符合弹性模量低而泊松比高的一般规律,但这并不影响整体宏细观规律的适用性。

表1 平行黏结模型细观参数正交试验设计

表2 平行黏结模型细观参数正交矩阵序列及数值模拟结果
2.2 多因素方差分析
多因素方差分析是研究多个自变量对一个因变量是否具有显著影响的统计学分析方法。方差分析采用F检验,查F表并作出判断。若计算的F远小于显著性水平的临界值,则认为对自变量的影响不显著,反之显著。使用SPSS(statistical package for the social sciences)软件计算时,也会给出概率相伴值Sig.,假设取显著性水平为α=0.05,若Sig.≤α,则自变量对因变量产生显著影响。若Sig.>α,则自变量对因变量无显著影响。

多因素方差分析的结果如图3所示,可得出以下结果。

图3 多因素方差分析F统计量Fig.3 Multivariate analysis of variance F statistic
(1)图3(a)中颗粒模量与半径乘子的概率相伴值Sig.均小于0.05,则对宏观参数弹性模量E产生显著影响,从F统计量看,摩擦角、颗粒半径与刚度比的影响程度处于弱势,黏结强度几乎不对弹性模量产生影响。
(2)图3(b)中刚度比与半径乘子的概率相伴值Sig.均小于0.05,对泊松比μ产生显著影响,其余参数影响不大,对比F统计量刚度比对泊松比的影响最大。
(3)图3(c)中主要由法向黏结强度与切向黏结强度对抗压强度产生显著影响,其余细观参数中仅有半径乘子的概率相伴值Sig.小于0.05,但相比于黏结强度的F统计量,其影响程度甚微,颗粒模量的Sig.接近于1,几乎不影响抗压强度,该宏观参数最易标定。
(4)图3(d)中黏聚力主要受切向黏结强度与法向黏结强度影响,半径乘子与摩擦角的影响程度不大,参考抗压强度影响参数,黏结强度细观参数直接影响宏观强度。
(5)图3(e)内摩擦角受多种细观参数影响,包括摩擦角、切向黏结强度和颗粒模量。其中摩擦角与切向黏结强度影响最为明显,颗粒模量次之,其余参数无明显影响。
2.3 回归分析
根据以上方差分析结果可知,宏观参数可由多个细观参数影响,但并不是所有都能达到显著影响条件,即Sig.≤0.05。因此在进行回归分析时,剔除非显著性影响参数,只对个别达到显著影响因素(Sig.=0.000)进行分析,以下对上述定性分析进行定量描述。


(2)
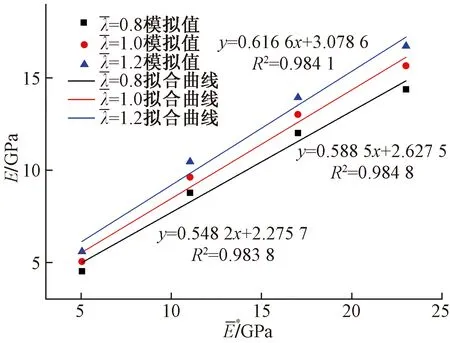
图和对弹性模量E的影响Fig.4 Influence of elasticity modulus E

μ=0.151 4lnk*+0.005 03
(3)


(4)


(5)
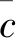
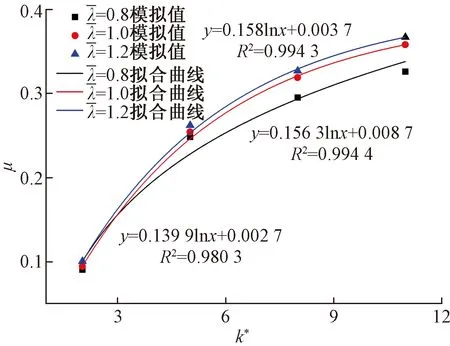
图5 k*和对泊松比μ的影响Fig.5 Influence of poisson ratio μ
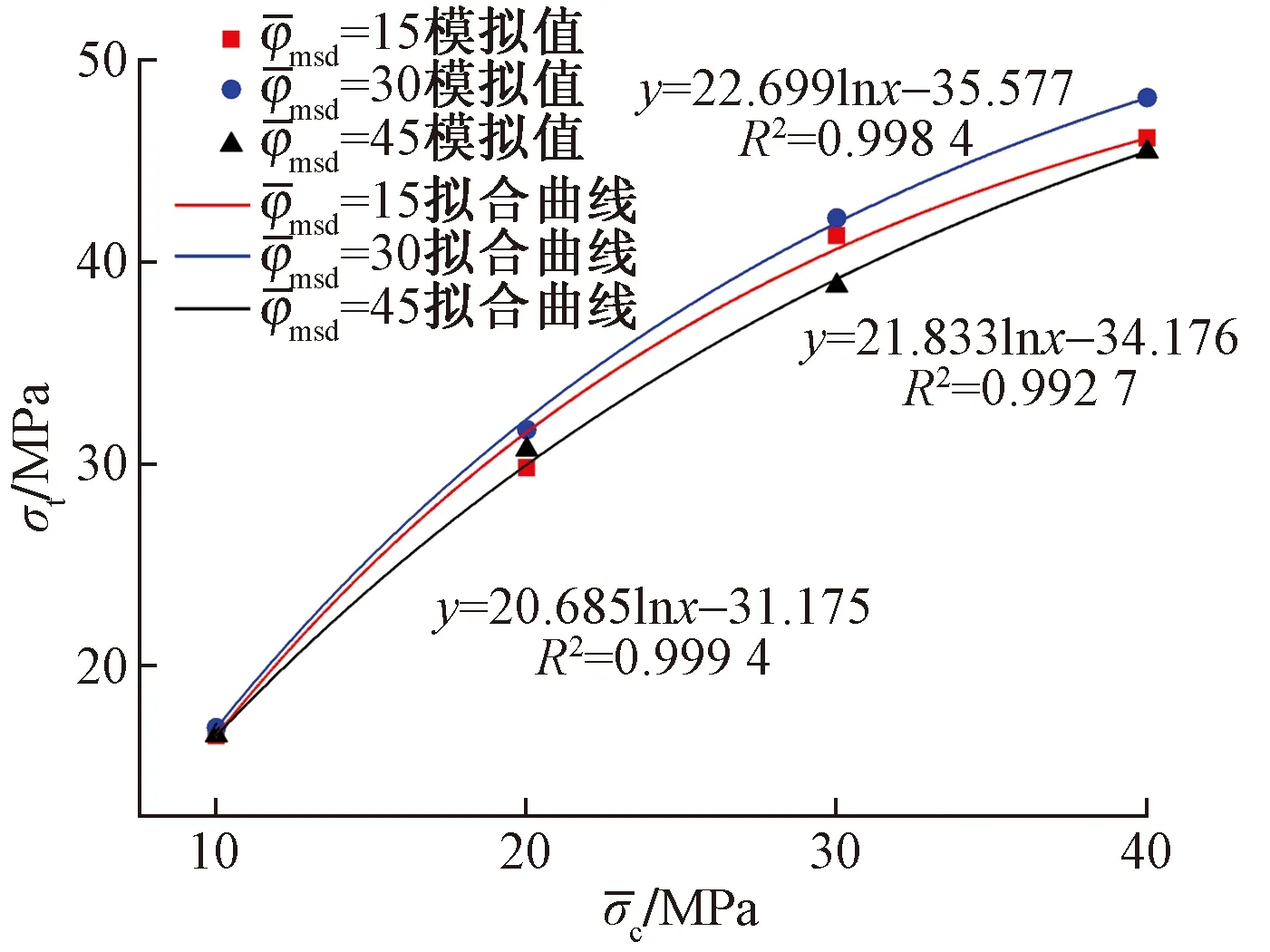
图和对抗压强度σt的影响Fig.6 Influence of on compressive strength σt

图和对黏聚力c的影响Fig.7 Influence of on cohesion c
逐渐增大,仅考虑显著因素的影响,内摩擦角φ的定量表达式为

(6)

图和对内摩擦角φ的影响Fig.8 Influence of on internal friction angle φ
3 细观参数快速标定方法及实例验证
3.1 平行黏结模型标定参数流程
根据回归分析中得到的拟合公式,若已知宏观参数可反演出对应的细观参数,由于拟合公式仅选取显著影响因素,在进行某一参数标定时,可先将其他细观参数设定较小值,利用反演公式逐一确定。细观参数反演公式如表3所示。

表3 细观参数反演公式
根据上述反演公式,对应快速标定流程如下:

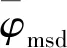
3.2 类岩石常规三轴试验
为验证上述标定方法与反演公式的可行性与正确性,将打磨后的试件在RMT-301岩石与混凝土力学伺服压力机进行力学实验,测定E、μ、σt、c、φ。每组4个试样,实验结果取平均值,具体结果见表4。

表4 物理试验与数值模拟结果
表4为物理试验与数值模拟的宏观力学参数值。弹性模量E误差为2.2%,泊松比差值为0.02,单轴抗压强度误差为0.18%,常规三轴试验不同围压下的峰值应力接近,最大误差为1.1 MPa,其中黏聚力c差值为0.71 MPa,内摩擦角误差为8.6%。尽管数值模拟与物理试验的裂纹扩展模式几乎一致(图9),但数值差异很大,其原因可能是采用纯圆颗粒导致颗粒之间咬合不足,无法抑制颗粒的旋转所造成。

图9 巴西劈裂试验裂纹扩展Fig.9 Crack propagation in Brazilian splitting test
5个宏观参数需由7个细观参数标定,结合三轴试验结果,代入表3的公式反演,可初步确定该类岩石材料的细观参数。再根据全应力应变曲线,微裂纹破坏特征等微调细观参数,最终调试的细观参数如表5所示。

表5 类岩石材料细观参数
3.3 应力-应变曲线
宏观应力-应变曲线能反应岩石的参数演化规律。该类岩石材料常规三轴应力-应变曲线如图10所示。数值试验与物理试验在弹性阶段基本一致,但斜率略低于物理试验。是由于颗粒流模型无天然裂隙与孔隙存在,在压密阶段保持线性增长。而天然岩石或人工制备的类岩石材料存在裂隙或孔隙,在初试伺服阶段,应力-应变曲线会微微上翘,再保持线性增长。不同围压下的峰值应力基本一致,残余强度比较接近,围压越大,应力软化越不明显,即软化段下降率降低。

图10 物理试验与数值模拟常规三轴应力-应变曲线Fig.10 Physical test and numerical simulation of conventional triaxial stress-strain curve
3.4 裂纹演化
五级不同围压加载试验破坏形态如图11所示,室内试验中试样的主破坏面与水平面呈夹角为62°左右,在主裂纹附近存在多条微裂隙。数值模拟同样存在一条60°的主贯通面,由张拉裂纹产生,剪切裂纹随机分布于主破坏面周围,且随围压增大,裂纹数量也逐渐增大。模拟结果与室内试验相近。常规三轴裂纹的破坏模式表明正交试验设计的7个参数对数值试验是可靠的。

图11 常规三轴裂纹扩展模式Fig.11 Conventional triaxial crack growth model
4 结论

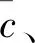
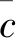
(4)基于平行黏结模型宏细观参数分析,尝试设计正交试验得到类岩石细观参数,通过常规三轴加载试验及劈裂试验验证了细观参数的可靠性,为课题组下一步研究节理岩体剪切力学特性提供依据。
