面向不平衡数据集融合Canopy和K-means的SMOTE改进算法

郭朝有，许 喆，马砚堃，曹蒙蒙

(海军工程大学动力工程学院,武汉 430033)

在类别数量上分布不均衡的数据集称为不平衡数据集[1],一般将类别数量多的数据样本称为多数类,类别数量少的数据样本称为少数类。不平衡数据集在信用卡诈骗、医疗诊断、网络入侵、故障诊断、网络事件发现等领域均广泛存在[2-4],如何利用现有分类算法对不平衡数据进行有效分类是数据挖掘领域面临的挑战之一[5]。目前,主要从两个方面解决不平衡数据集的分类问题:一是从数据层面出发,利用数据平衡化方法使数据集达到平衡,如过采样或欠采样技术[6]等；二是从算法层面出发,通过改进现有算法使其能够针对性地处理不平衡数据,如代价敏感学习[7]、集成学习[8]和单类学习[9]等。

过采样或欠采样技术通过人为地增加或减少原始不平衡数据集中的少数类或多数类样本以改变数据样本的不平衡分布,从而使新的数据集在类别数量上达到平衡。Chawla等[10]提出的(synthetic minority over-sampling technique, SMOTE)算法是最为经典的启发式过采样技术,该算法在少数类样本和其近邻样本之间利用随机线性插值的方法合成新的少数类样本。但因对少数类样本进行无差别地选择,导致其合成样本质量不高。为此,Han等[11]提出了Borderline-SMOTE算法；Yen等12提出了先聚类再抽样的数据平衡化方法；曹正凤[13]提出了C_SMOTE算法；陈斌等[14]提出了KM-SMOTE算法,该方法先利用K-means算法聚类,然后再运用SMOTE算法进行过采样；刘丹等[15]提出了一种最近三角区域的NNTR-SMOTE算法,使生成的样本不突破原始类别边界地更接近少数类。虽然上述改进方法在一定程度上改善了数据集的不平衡分布,但也存在着一些不足,如数据样本分布模式改变、数据样本重叠导致合成样本有效性不足等。

综合上述SMOTE改进算法,本文融合Canopy和K-means算法优点,对SMOTE平衡化方法进行改进,并将其定义为C-K-SMOTE算法,然后利用随机森林算法开展了分类实验。

1 相关算法

1.1 Canopy算法

Canopy算法[16]基于欧式距离测度等快速距离测度和距离阈值T1、T2(T1>T2),将数据划分成一些重叠的簇(canopy簇)以实现近似聚类,是一种快速近似聚类技术,能够实现海量高维数据的聚类分析。

Canopy算法基本流程如下：

(1)根据数据集的特征或通过多次交叉实验优选确定距离阈值T1和T2。

(2)数据集中任取一点A,若无canopy簇存在,则把A点当作第一个canopy簇,否则计算A点与各个canopy簇簇心间距离D={D1,D2,…,Dk}(k为canopy聚类簇簇数)。

(3)比较D与T1和T2,若D≤T1,则点A归入相应的canopy簇,并根据canopy簇中各点几何平均值重新调整canopy簇的簇心；若D≤T2,则将点A从数据集中剔除；若D>T1,则将生成一新的canopy簇,并以点A作为该canopy簇的簇心。

(4)重复执行步骤(2)和(3),直至数据集为空,算法结束。

该算法原理简单、易于实现,由于采用了简单快速的距离测度,使得其计算耗时少,数据划分效率高,可迅速地对大量数据进行粗略聚类。此外,该算法无需事先设定聚类簇数,避免了随机确定聚类簇数的盲目性。但也正是由于其距离测度的简单化也导致其聚类输出的聚类精度不高。

1.2 K-means算法

K-means算法[17]核心思想:基于Euclidean Distance Measure等距离测度,结合预设聚类簇数k和初始聚类中心,通过不断迭代运算,实现数据集的划分聚类。基本流程如下。

(1)数据集中随机选择k个点作为初始聚类中心(k为聚类簇簇数)。

(2)计算剩余数据到k个聚类中心的距离,将它们划分至距离最近的簇中。

(3)计算每个聚类簇中所有数据样本的平均值,将其作为新的聚类中心,并计算目标函数E。

(4)重复步骤(2)和(3),直至聚类中心不再变化或E达到收敛条件,算法结束。

目标函数E如式(1)所示,E越小,聚类效果越好。

(1)

式(1)中：xi表示数据集中第i个数据样本；ωj表示第j个聚类簇；zj表示第j个聚类簇的簇心。

该算法原理简单、易于操作且能够快速收敛,能够高效地处理大规模数据。但也存在一定的不足,如聚类簇数k选取盲目和初始聚类中心敏感等。

1.3 SMOTE算法

SMOTE算法基于在相距较近的少数类样本之间仍然存在少数类样本的假设,采用随机线性插值的方法在少数类样本之间合成新的样本,进而使不平衡数据集趋向平衡。基本流程如下：

(1)获取不平衡数据集中的少数类样本{X1,X2,…,Xn}。

(2)基于欧氏距离求取每个少数类样本的m个最近邻样本{Yi1,Yi2,…,Yim}。

(3)在少数类样本与其m个最近邻样本之间进行随机线性插值处理,这样每个少数类样本Xi经过插值都可以得到m个合成样本Pj(j=1,2,…,m)；

(4)将插值得到的少数类样本放入不平衡数据集中,得到新的数据集并计算不平衡度。

(5)若不平衡度已达到要求,则程序结束,否则转步骤(1)。

其中,随机线性插值公式为

Pj=Xi+rand(0,1)(Yij-Xi)

(2)

式(2)中,Xi为少数类样本；Yij为与Xi相邻的m个最近邻样本；rand(0,1)为(0,1)区间的随机数。

2 C-K-SMOTE改进算法

2.1 SMOTE算法问题

深入分析SMOTE算法,并结合相关文献,总结其存在的自身难以克服的问题[18]如下：

2.1.1 近邻样本选择盲目性问题

SMOTE算法合成的新样本与每个少数类样本的m个最近邻值密切相关,因此,近邻值的选取关乎着合成样本的数据质量,但m的选择具有一定的盲目性。

2.1.2 样本分布模式失真问题

数据集均存在一定的原始分布模式,而SMOTE算法在合成少数类样本时,未考虑数据集的原始分布,极易导致新生成的数据会影响原来的分布模式。

2.1.3 样本边界模糊化问题

当对处于多数类和少数类边界处的少数类样本进行过采样时,新生成的数据也会位于样本边界附近,从而使得少数类样本越来越边缘化,进而造成多数类与少数类的边界越来越模糊。

2.1.4 插值样本失效问题

SMOTE算法合成新样本时,不能很好地处理少数类样本存在噪声数据的情况,往往会导致合成样本有效性不足。

2.2 C-K-SMOTE算法

针对SMOTE算法存在的上述不足,借鉴曹正风提出的C_SMOTE算法和陈斌提出的KM-SMOTE算法,融合Canopy和K-means聚类算法,形成了一全新的SMOTE改进算法——C-K-SMOTE。C-K-SMOTE核心为:利用Canopy算法对少数类样本进行快速近似聚类,得到一系列canopy簇；然后再利用K-means聚类算法对canopy簇再聚类,得到精准聚类簇,最后再利用SMOTE算法基于精准聚类簇进行插值处理,从而增加少数类样本数量使数据样本趋向平衡。

2.3 C-K-SMOTE算法核心步骤

(1)少数类样本的粗、细聚类,得到精准簇。运用Canopy算法进行粗聚类,生成以A、B和C为簇心的三个canopy簇；运用K-means算法对canopy簇进行再聚类,得到三个精准簇,经过不断的划分和初始中心优化调整之后,三个精准簇的中心分别为C1、C2和C3,聚类过程示意图如图1所示。

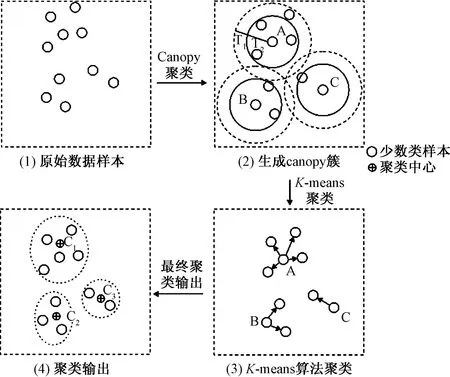
图1 基于Canopy算法和K-means算法对少数类样本聚类Fig.1 Clustering of minority samples based on Canopy and K-means algorithm

(2)基于精准簇随机插值合成新数据集。基于步骤(1)得到的精准簇,运用SMOTE过采样算法,采用修正的随机插值公式即可合成新样本,如图2所示。

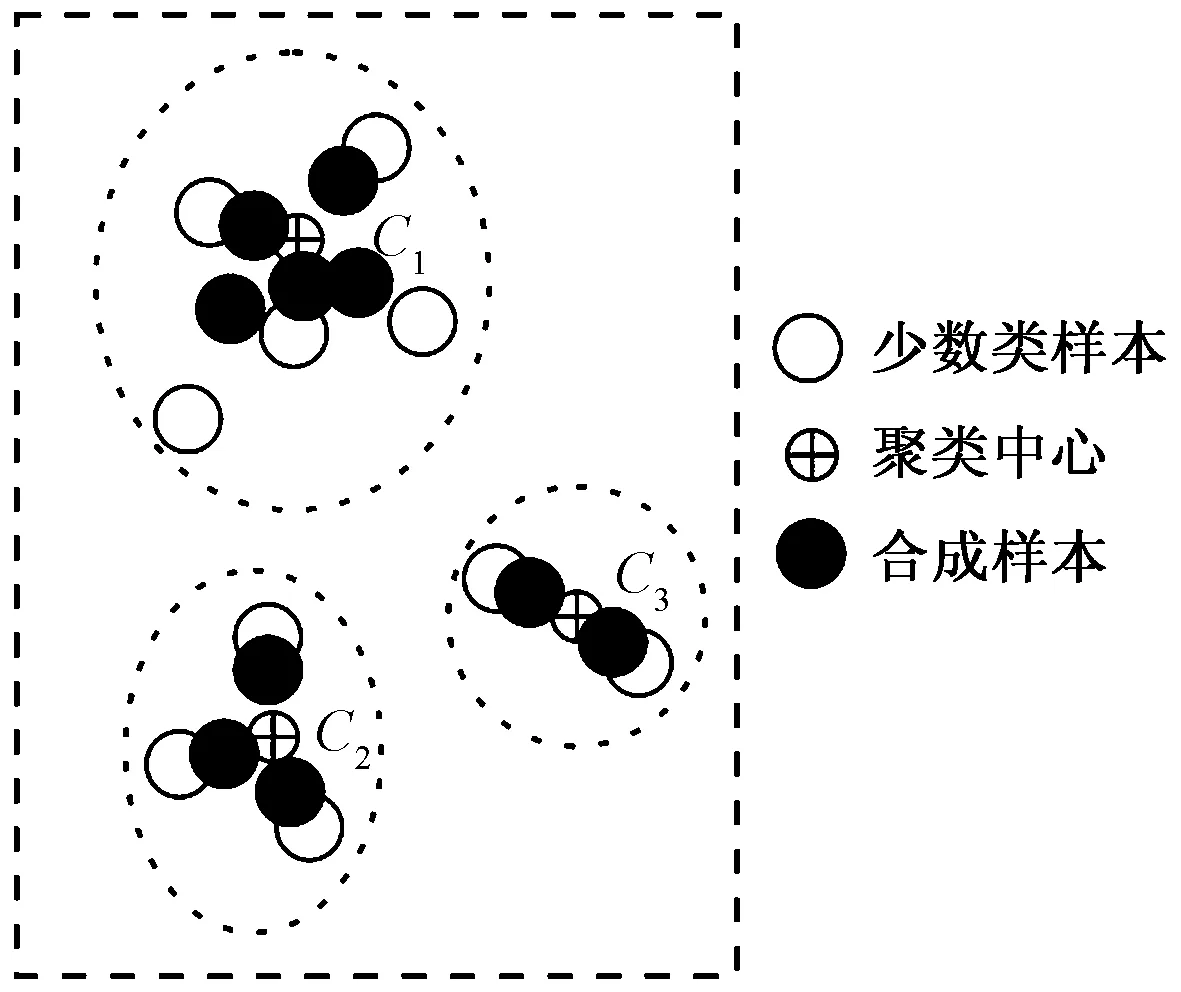
图2 基于CKSMOTE算法合成新样本Fig.2 Synthesis new samples based on CKSMOTE algorithm

其中修正的随机插值公式为

Pi=Xi+rand(0,1)(ut-Xi)

(3)

式(3)中：Xi(i=1,2,…,n)为少数类样本,n表示少数类样本总数；ut(t=1,2,…,k)为精准聚类簇簇心,k表示聚类簇数；Pj(j=1,2,…,m)为合成的新数据,m表示新合成数据的总数。rand(0,1)表示(0,1)区间的随机数。

3 算例验证

3.1 数据集

算例数据集来自于公开数据集KEEL(knowledge extraction on evolutionary learning)数据库[19]中的不平衡数据集,共选取了Yeast、Ecoli和Page-blocks三组不同不平衡度的数据集(如表1所示)，并采用10倍5折交叉验证方法将数据集划分为训练集和测试集。

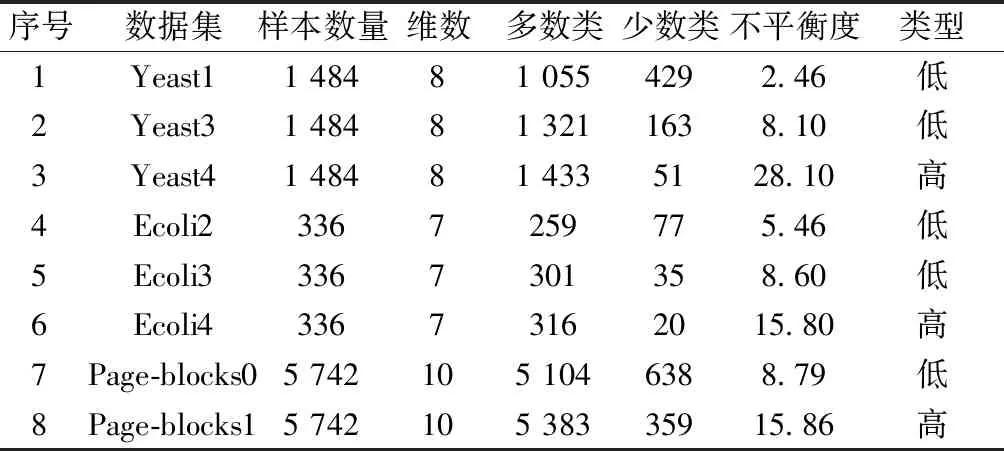
表1 测试数据集Table 1 Testing data sets

3.2 评价指标

由于不平衡数据本身的特殊性,仅凭某单一性能指标无法综合评价基于不平衡数据的分类性能,为此,优选G-means和TP/FP(ture positive/false positive)散点图作为不平衡数据集分类效果的综合评价指标。

基于表2的混淆矩阵,可定义真正率(TPrate)、假正率(FPrate)等其他常见的性能评价指标,如表3所示。

表2 混淆矩阵Table 2 Confusion matrix for binary classification

表3 其他的性能评价指标Table 3 Extra performance evaluation indicators

G-means是真正率和真负率乘积的平方根,如式(4)所示:

(4)

G-means综合了真正率、真负率,较好地反映了面向不平衡数据集的整体分类能力。

TP/FP散点图是反映分类器正确分类率和错误分类率之间关系的可视化表示方法,是以假正率(FPrate)为横轴,真正率(TPrate)为纵轴的二维曲线图,如图3所示。

图3 TP/FP散点图Fig.3 TP/FP scatter plot

图3中每个点(FPrate,TPrate)对应一个分类器模型。当FPrate越小且TPrate越大时,分类模型的分类效果越好；在TP/FP散点图上表现为越靠近左上方,分类性能越优。

3.3 实验

为对比测试SMOTE算法和CKSMOTE算法的数据平衡化性能,设计了如下三组实验方案。其中随机森林的决策树数目设定为100,SMOTE算法的最近邻值设定为3[20]。

方案一运用RF算法对原始不平衡数据进行分类

方案二运用RF算法对利用传统SMOTE算法平衡化后的数据集进行分类

方案三运用RF算法对利用C-K-SMOTE算法平衡化后的数据集进行分类

3.4 实验结果及分析

按上述实验方案对表1所列8个不平衡数据集进行实验,实验G-means如表4所示。表4所列为实验G-means指标值,转换为柱状图为图4所示。

表4 实验G-means指标值Table 4 G-means indicator of the experiment

图4 实验G-means指标柱状图Fig.4 The histogram of G-means indicator

由表5、图4分析可得以下结果。

(1)CKSMOTE+RF模型在8个数据集上的G-means值均高于SMOTE+RF模型,平均提高了8%左右,这表明CKSMOTE算法相比传统的SMOTE算法在处理不平衡数据时的平衡效果更好,在提升随机森林算法分类效果上更为显著。

(2)数据集的不平衡度越高,C-K-SMOTE算法的数据平衡化性能更好。以Yeast数据集为例,相比于SMOTE算法,Yeast1、Yeast3和Yeast4数据集C-K-SMOTE算法的G-means分别提高了5.66%、5.78%和26.47%。

TP/FP散点图如图5所示。

图5 TP/FP散点图Fig.5 TP/FP scatter plot

由图5分析可得以下结果。

(1)C-K-SMOTE+RF模型在8个数据集下的TPrate均比SMOTE+RF算法有提升,平均提高了约4.48%,同时FPrate均有所降低,平均降低了约22.02%。即相比SMOTE+RF模型,C-K-SMOTE+RF模型平衡化不平衡数据性能更优,随机森林分类效果提升程度更高。

(2)数据集的不平衡度越高,C-K-SMOTE+RF模型的平衡化效果越显著。以Page-blocks数据集为例,由TP/FP散点图可以看出,经CKSMOTE改进算法平衡化处理后,数据集Page-blocks0和Page-blocks1Ecoli4的坐标位置相比于SMOTE+RF算法更趋近于左上角(0,1)的位置,这直观地表明了CKSMOTE改进算法能够更好地平衡不平衡数据集,同时也能改善随机森林的分类效果。

综合上述G-means值和TP/FP散点图的分析,设计的C-K-SMOTE算法在平衡化处理不平衡数据集时效果更优,CKSMOTE+RF分类模型对少数类样本识别准确率更高,特别是对于不平衡度较大的数据集,其效果更加显著。

4 结论

针对SMOTE算法存在的问题,结合Canopy和K-means算法,设计一种新的C-K-SMOTE改进算法:采用“先聚类后插值”的方法,既保证了新生成的样本的有效性也保留了原数据分布模式且不存在边界模糊问题；利用修正的SMOTE算法插值公式避免了近邻样本选择盲目性问题；实现了Canopy算法和K-means算法有机融合,利用K-means再聚类解决了Canopy算法聚类精度低的问题,同时利用Canopy聚类克服了K-means算法聚类簇数难以确定以及初始中心过于随机的问题。

基于公开数据集的算例,验证了改进算法的有效性。但该算法也存在一定的不足,如Canopy算法中两个距离阈值T1和T2的选取,采用多次实验交叉验证方法进行设定,虽然该方法快速有效,但仍具有一定的随机性和盲目性,还需要进一步的深入研究。