南京大胜关长江大桥轻轨列车走行性研究
2020-09-04马舜李小珍张弘肖林
马舜 李小珍 张弘 肖林
(1.中铁大桥勘测设计院集团有限公司,南京 210000;2.西南交通大学土木工程学院,成都 610031)
目前车桥耦合振动的理论研究已经比较完备[1-4],以车桥耦合振动理论为基础,关于不同轨道结构形式、桥梁结构特征以及环境荷载特征的车辆、桥梁结构的响应分析层出不穷[5-7]。随着城市建设的发展,越来越多的轨道交通(轻轨、地铁)使用桥梁作为轨下基础,但在大跨度桥梁上承载轨道交通的情况尚不多见,相关研究并不充分。
南京大胜关长江大桥是国内首座在高速铁路桥上搭载城市轨道交通的桥梁,轻轨托架的支撑刚度、高铁列车与轻轨列车运行干扰等对轻轨列车走行性的影响有待深入研究。本文基于车桥耦合振动分析理论,建立包含正线铁路结构以及悬挑轻轨结构的南京大胜关长江大桥车桥耦合振动分析模型,分析其列车运行时的车辆、结构响应,研究轻轨列车的走行性。
1 车桥耦合振动分析流程
车辆-线路-桥梁系统是一个复杂的多体、多态耦合系统,是桥梁结构动力学、车辆动力学、轨道动力学等学科的交叉。应用系统方法分别建立车辆、桥梁子系统,通过各子系统间的相互耦合作用,建立车辆-线路-桥梁系统动力学模型,考虑车辆系统中存在的轮轨接触几何非线性、轮轨蠕滑率及蠕滑力的非线性以及车辆一系、二系悬挂系统的非线性特性。在轮轨耦合模型中采用目前最完善的动态轮轨关系。
车辆的运动方程用矩阵形式可表示为
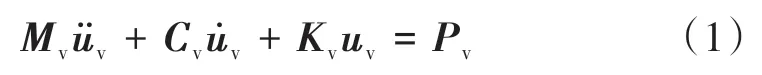
式中:Mv,Cv,Kv分别为车辆的质量、阻尼、刚度矩阵;分别为车辆的加速度、速度、位移列向量;Pv为车辆的荷载向量,一般是轨道不平顺及桥梁各自由度的函数。
桥梁的运动方程用矩阵形式表示为
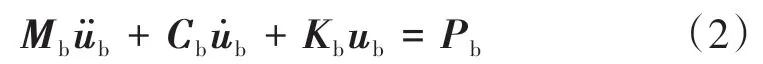
式中:Mb,Cb,Kb分别为桥梁的质量、阻尼和刚度矩阵;分别为桥梁的加速度、速度、位移列向量;Pb为桥梁的荷载向量,是车辆振动状态的函数。
求解式(1)、式(2)组成的方程组时,其右端项Pv与Pb通过轮轨关系关联在一起,以车轮-钢轨相互作用力的相对误差小于允许误差作为收敛条件。轮轨法向力通过Hertz 非线性弹性接触理论计算;轮轨蠕滑力基于Kalker 线性蠕滑理论和沈氏理论进行计算[3-4]。车桥耦合振动响应是复杂的时变动力过程,本文基于时域分析对上述方程组编程求解。采用多刚体动力学方法建立车辆动力学子系统模型,并采用显式积分法求解;采用有限元方法建立桥梁子系统模型并采用隐式积分法中的Newmark-β积分法求解其动力响应。
2 分析模型
2.1 桥梁模型
南京大胜关长江大桥承载沪汉蓉快速客运通道和京沪高速铁路四线铁路,在主桁架外侧分别挑出5.2 m的悬臂托架支撑南京地铁S3号线(轻轨)。该桥为(108+192+336+336+192+108)m 连续钢桁拱结构,轨道交通采用由纵梁、横梁组成的格子梁体系的明桥面结构承载。轻轨托架悬挑在下弦边主桁的外侧,与节点处的横梁等高,为焊接的工形板梁。轻轨纵梁为一组高0.9~1.1 m的工形梁,间距2.0 m,用联结系角钢相连。该桥轻轨托架通过栓接、焊接连接在主桁节点板上,由于托架的长度与高度较小,其节点刚度介于铰接与固结之间。因此,在桥梁结构分析中必须考虑节点刚度的影响。通过板壳模型(图1)计算结果得到杆系分析模型的节点刚度。
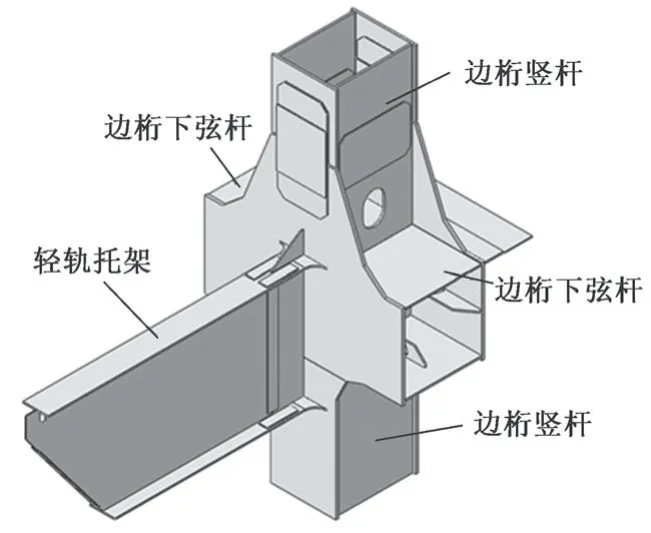
图1 轻轨托架的板壳模型
采用MIDAS/Civil 软件建立主桥连续钢桁架拱的杆系模型(图2),将模型中的单元、节点、质量、阻尼等结构参数导入车桥耦合振动分析程序。

图2 桥梁结构杆系分析模型
2.2 车辆模型
轻轨列车是由车体、转向架构架、轮对等基本部件组成的多自由度系统。研究表明,不同车辆模型与自由度数目对车桥空间振动响应影响较大;按等效一系悬挂处理的车辆模型不能真实反映车辆振动的实际情况;将同一转向架下的轮对合并成一个等效轮对会导致车桥竖向振动响应偏大。本文采用地铁B 型车,车辆主要参数见表1;采用考虑一系、二系悬挂23个自由度的车辆模型(图3)来进行分析,其中车体考虑5 个自由度,即横向(yc)、垂向(zc)、侧滚(φc)、摇头(ψc)、点头(βc);x为车辆行进方向。
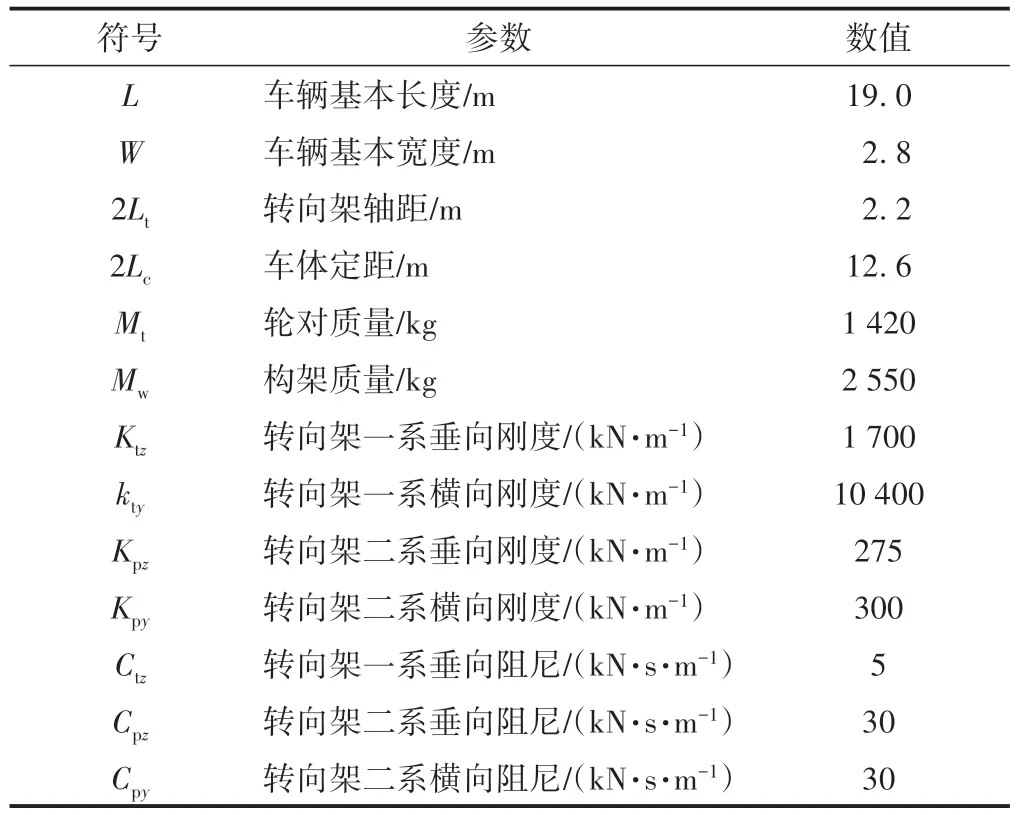
表1 车辆主要参数
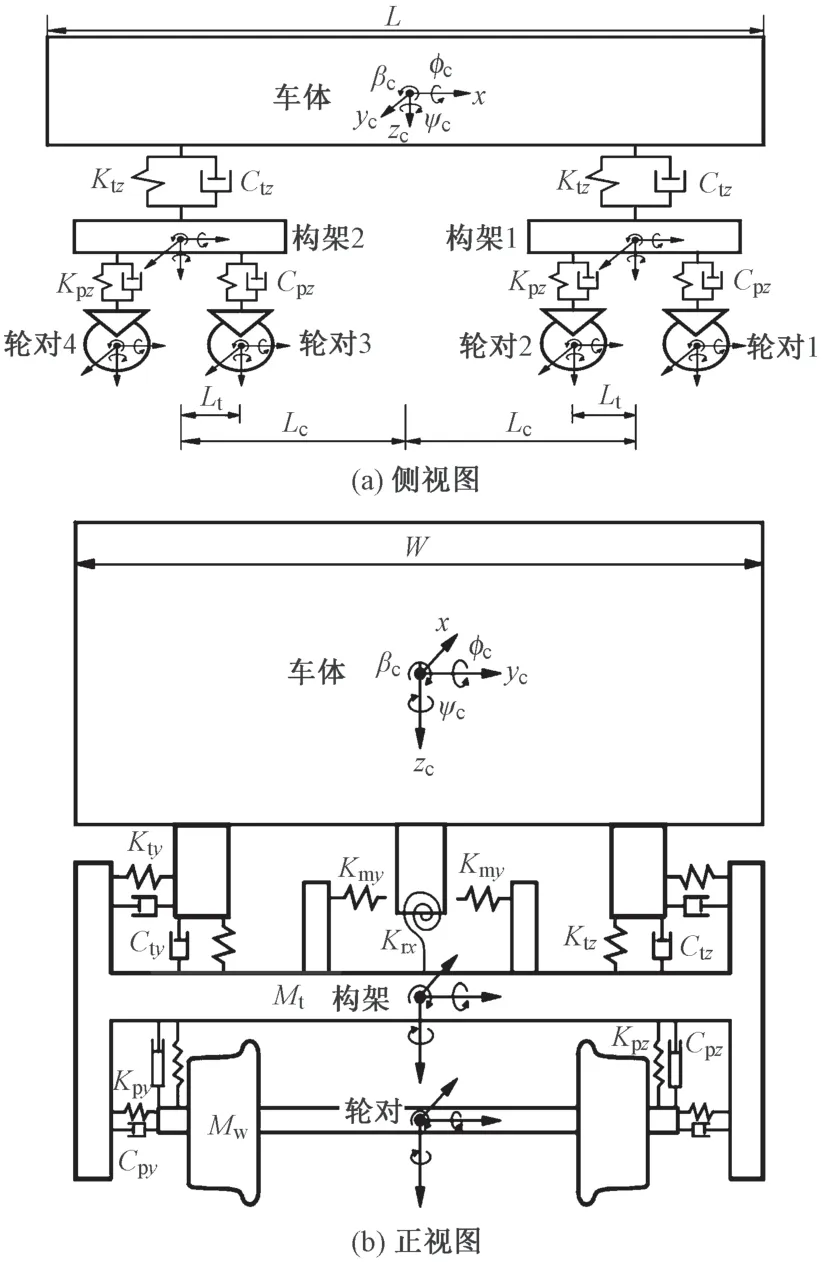
图3 车辆动力学模型
车型编组为动+拖+动+动+拖+动。不同负载状态下车辆的静轴重见表2。

表2 不同负载状态下的车辆静轴重 t
2.3 轨道不平顺
轨道不平顺是车辆振动的关键影响因素。根据桥梁的线路状况及轻轨运营速度,选取美国6 级谱作为轨道不平顺输入。根据功率谱转换得到的不平顺样本序列长2 000 m,不平顺测点间距0.5 m,见图4。
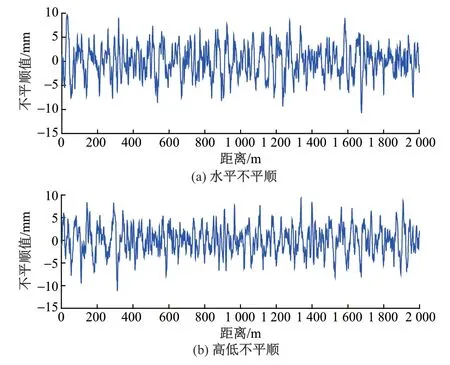
图4 时域不平顺样本
3 结果分析
考虑不同车速(v=40,60,80,100 km/h)及轨道交通负载状态(空载、定员、超员)下车辆和桥梁的动力响应,对该桥列车走行性进行分析。
3.1 桥梁振动响应
分析结果表明,轻轨列车过桥时连续钢桁拱动力响应最大处为6#—7#墩间主桁与主拱。各种负载状态的轻轨列车以v=100 km/h 过桥时,6#—7#墩间主桁下弦跨中与拱顶位置的振动位移时程见图5。

图5 大桥6#—7#墩间典型位置振动位移时程(v=100 km/h)
由图5 可知,超员状态下,主桁下弦跨中的横向、竖向振动位移最大值为2.450,20.298 mm,分别为空载状态下的1.66 倍和1.44 倍;主桁拱顶处横向、竖向振动位移最大值为16.134,18.783 mm,分别为空载状态下的1.83 倍和1.65 倍。车辆负载状态对桥梁的位移影响较大,超员状态下桥梁位移响应最大,定员次之,空载状态下最小。
3.2 车体振动响应
各种负载状态的轻轨列车以速度v=100 km/h 通过时,轻轨动车及拖车的振动加速度时程见图6。
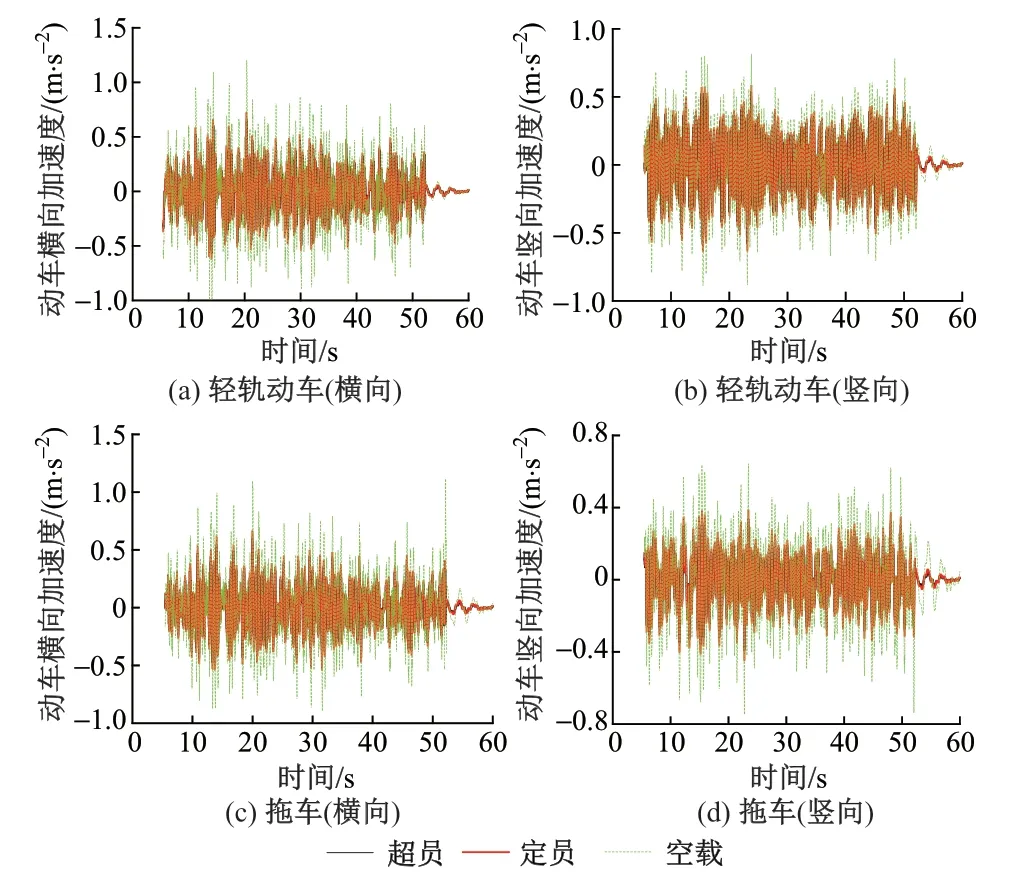
图6 轻轨动车及拖车振动加速度时程(v=100 km/h)
由图6 可知,超员状态下,轻轨动车的最大横向、竖向振动加速度为0.662,0.587 m/s2,分别是空载状态下的0.55 倍和0.66 倍;拖车的最大横向、竖向振动加速度分别为0.599,0.483 m/s2,分别是空载状态下的0.55 倍和0.53 倍。车辆负载状态对车体振动响应影响较大,超员状态下车体振动加速度最小,空载状态下最大。
3.3 轻轨列车走行性指标
基于各工况计算得到的车辆轮轨力、振动加速度等时程结果,根据规范[8-9]可得到脱轨系数Q/P、轮重减载率P/P0、倾覆系数Pd/P0、舒适性指标(Sperling 指数)等列车走行性指标,其中Q为轮对横向力,P为垂向力,P0为静轴重,Pd为单侧轮轨垂向动荷载。不同运行状态轻轨列车动车过桥时各项指标的最大值见表3。可知,车辆负载状态对其运行状态影响较大。整体上,脱轨系数、轮重减载率、倾覆系数、车体振动加速度、舒适度指标均随轴重的减小而增大。因此,轻轨列车的安全性主要由空载状态控制。
对轻轨列车运行安全性与舒适性进行评价。各种运行状态下的脱轨系数、轮重减载率、舒适度指标均小于规范[8-9]限值(分别为0.8,0.6,2.5),表明列车运行安全性、舒适性均满足要求。
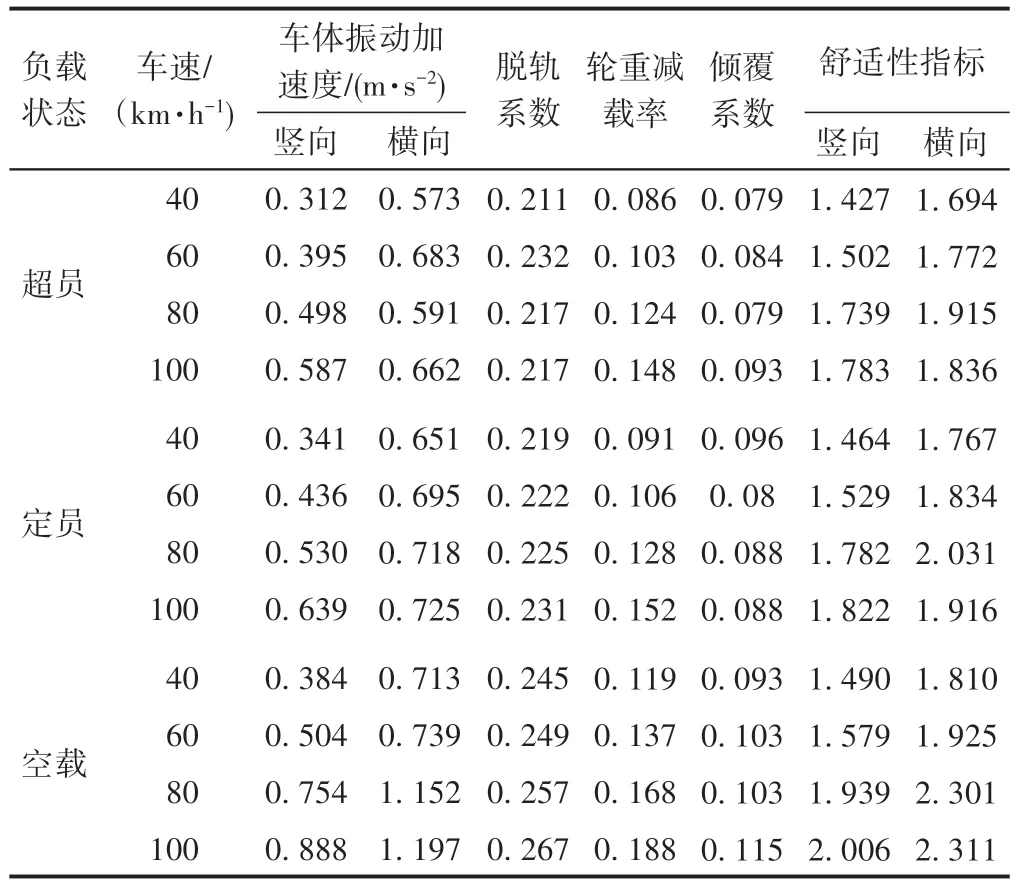
表3 轻轨列车的走行性指标
4 结论
本文结合南京大胜关长江大桥搭载轨道交通结构,基于车桥耦合振动分析理论对其列车走行性进行分析,得出如下结论。
1)车辆负载状态对桥梁的位移影响较大。超员状态下桥梁位移响应最大,空载状态下最小。
2)车辆负载状态对车体振动响应影响较大。超员状态下车体振动加速度最小,空载状态下最大。
3)车辆负载状态对其运行状态有较大的影响。轻轨列车的安全性主要由空载状态控制。
4)轻轨列车以40~100 km/h 的运行速度过桥时,对于空载、定员、超员状态,桥梁结构响应均较小,列车运行安全性、乘坐舒适性均满足规范要求。
