基于EMD-PSO-ELM的基坑变形时变序列预测研究
2020-09-04王景春宋培林王炳华何旭升
王景春,宋培林,王炳华,何旭升
(1.石家庄铁道大学土木工程学院,石家庄 050043; 2.南宁轨道交通集团有限责任公司,南宁 530029)
引言
基坑变形对于基坑的安全施工起着关键的影响作用,在施工过程中应及时对其进行监测,以确保准确掌握基坑的变形信息,这对于基坑的安全预警是十分有效的途径[1]。基坑变形是引起基坑发生坍塌的最主要因素,其本身便携带有多种引发基坑坍塌的关键信息,在外界自然条件、时空效应等非线性因素的综合作用下,基坑的变形体现出明显非平稳性特点,且在施工过程中受施工工序、场地条件等因素的影响给变形预测工作增加了一定的难度。目前深基坑工程多位于城市人流量密集,建筑物复杂的地铁车站地区,各种非稳定性因素都可能会造成施工过程中事故的发生,带来无法估量的后果。因此,从基坑变形的时序序列出发,基于监测数据掌握基坑的非平稳变形规律,实现精准的实时动态预测,对于防治基坑变形、坍塌的发生,实现基坑的安全施工具有重要意义。
对于基坑变形的预测,国内外学者从不同方面进行了研究并取得了一定的成果。PROTOSENYA A.G.等[2]通过三维数值模拟深基坑施工过程,对其产生的土体变形进行了预测;Benin Andrey等[3]通过考虑基坑施工的阶段性,对基坑结构以及周围建筑物的变形做出了评价;焦仓等[4]结合现场监测的支护变形资料,通过优化土体m值利用有限元软件对基坑变形进行预测;任超等[5]通过提出一种集合经验模态分解的方法来预测大坝的时序变形,与传统的神经网络方法相比其结果精确度有了明显提高;吴欢等[6]利用粒子群算法改进的支持向量机对基坑的变形进行预测,得到改进的预测模型,最终预测结果与监测数据拟合度相对较好;李思慧等[7]将局部均值分解(LMD)与神经网络相结合,建立了基于时变序列的基坑变形预测模型;王涛等[8]运用RBF神经网络对基坑变形的时变序列进行预测,通过误差下降和高斯函数中心宽度调节的方法,从而对RBF神经网络模型的预测精度进行了提高;方林胜等[9]将灰色理论与神经网络相结合,建立了地铁深基坑变形预测模型;郭建等[10]依据小波分解理论对深基坑变形的时序序列进行分解,建立了预测深基坑变形的小波分解模型。和常见的神经网络预测模型相比粒子群算法具有收敛速度快、通用性强的特点,对于预测基坑变形较为有效。虽然上述神经网络预测模型一定程度上对于基坑变形的非平稳特性有所体现,但是基坑变形的时序序列所表现出来的物理特性,携带信息的意义并未从深层次进行挖掘。神经网络预测模型固有的缺点,监测数据的误差都严重影响着预测结果的准确性。故预测模型在基坑变形的非平稳变化特性上和其预测精度上有待进一步提高。
经验模态分解(EMD)算法将复杂的非平稳信号进行去噪处理,分解成多维度携带有不同物理意义的本征模态函数(IMF),进而可以看出时序序列在空间各尺度上的分布规律[11]。极限学习机(ELM)是一种不需要多次迭代,只需要设置隐含层个数的适用于单隐含层前馈神经网络的高效学习方法[12]。粒子群算法(PSO)是在对生物种群行为进行观察的基础上得到启发,进而发展起来的求解优化问题的一种算法,该方法具有精度高、收敛快的特点[13]。本文将EMD、PSO、ELM三种算法结合起来建立基坑变形预测模型。采用经验模态分解将基坑变形的监测数据时序序列分解成多个具有物理意义的IMF分量,利用伪近邻法[14]重构相空间,利用重构后的时变序列对PSO-ELM模型进行训练和预测,得到最终变形预测结果。结合南宁市某地铁车站明挖基坑具体实例进行基坑变形量预测,以此验证模型的适用性。
1 模型原理与方法
1.1 经验模态分解(EMD)原理
针对非平稳信号的分析处理问题,HUANG等[15-16]在1998年提出了经验模态分解法(EMD)和连续均值筛选法,EMD通过将原始数据分解为不同维度的变化趋势,并引入了本征模态函数(IMF)理论对其不同的变化趋势进行解释,EMD算法通过对非平稳变化的信号进行去噪声处理,将信号分解为多维度的IMF函数,其基本原理如下:若原始信号数据x(t)中在零点上下的点数比其极大值或极小值的个数少2个及2个以上时,则该原始的信号数据应该利用EMD算法进行去噪处理,将处理后的原始信号数据分解为多维度的若干个IMF函数和一个残余分量R,这些分量体现出了原始数据不同时间维度内的信号信息。EMD算法进行分解基本步骤如下。
(1)若原始数据时变序列为x(t),首先找出原始数据中的全部极值点,利用3次曲线函数拟合出上下极值点的包络线,并求解出包络线的数据平均值,设为m1(t),则原始序列x(t)和m1(t)的差值为第一个分量,记作h1(t)
h1(t)=x(t)-m1(t)
(1)
(2)如果h1(t)符合IMF函数条件,则h1(t)为第一个满足条件的IMF分量,否则将h1(t)作为原始信号数据代入式(1),即
h11(t)=h1(t)-m11(t)
(2)
(3)重复进行以上筛选步骤k次,直到h1k(t)满足IMF条件为止。令h1k(t)=c1(t),则c1(t)为包含原始数据最优的第1阶IMF函数分量。
(4)将c1(t)从原始数据x(t)中分开得
r1(t)=x(t)-c1(t)
(3)
式中,r1(t)表示残余函数分量。将r1(t)作为新的原始数据并重复进行以上步骤,得到x(t)的第2阶IMF分量,如此进行n次循环,得到原始序列x(t)的n个IMF分量,其表达式为

(4)
(5)当rn(t)循环过程中再也无法分解出满足条件的IMF分量,此时循环宣告结束,得到最终原始数据x(t)的表达式如下

(5)
1.2 极限学习机(ELM)基本原理
极限学习机[17](ELM)是一种基于前馈神经网络构建的学习算法,较传统的神经网络具有模型简单易用、参数选取简单、泛化性能好等优点。
对于任意M个不同样本(xi,ti),其中xi=(xi1,…,xin)∈Rm,ti=(ti1,…,tin)∈Rm。若隐含层神经元个数为n,其标准形式如下
αi=(αi1,…,αin)T
(6)
根据零误差逼近原则,在该前馈神经网络中存在参数αi,bi,βi使得

(7)
式中,Fp(x)为输出向量;βi为第i个隐含层节点与输出层节点之间的权值向量;G(x)为激励函数;ωi为第i个隐含层节点与输入层节点之间的权值向量;bi为隐含层的神经元偏置向量。
式(7)可化简为:Hβ=Y,H为隐含层的输出矩阵。在ELM中随机确定阙值和权值,将输出矩阵H确定下来,β可以由式子β′=H+Y′求解得到。式中H+表示隐含层的输出矩阵的Moore Penrose广义逆。
1.3 PSO-ELM耦合算法
在大部分情况下ELM算法可以获得良好的效果,但算法中的阀值ω、权值b和隐含层的节点个数均会对其精度产生较大的影响。在算法的执行过程中可能会存在部分节点无效的情况,故在应用中需要大量的隐含层节点数才能使ELM算法获得预期的效果,而节点个数的增加将会使复杂度和运算量大大提高,使算法的泛化能力下降。故采用PSO算法优化极限学习机中的阀值和权值,以降低模型的复杂程度和运算量。粒子群算法(PSO)是由Eberhart和Kennedy在1995年提出的一种可以进行全局优化的算法,其基本原理为[18],若粒子处于D维空间,某个种群由n个粒子组成X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维向量Xi=[Xi1,Xi2,…,XiD]T,其含义为第i个粒子在D维空间中所处的位置,这也意味着此问题的潜在解。根据相对应的目标函数,即可求解出此粒子Xi所对应的适应度的值。则第i个粒子的速度为Vi=[Vi1,Vi2,…,ViD]T,其个体极值为Pi=[Pi1,Pi2,…,PiD]T,种群的全局极值为Pg=[Pg1,Pg2,…,PgD]T。粒子通过每一次的迭代相应地会更新自身的极值和全局极值的位置和速度。当逐渐达到满足条件时,迭代终止,更新后的公式如式(8)、式(9)所示。
(8)

(9)
具体优化步骤如下。
(1)给定包含输入向量和期望输出向量的学习样本。
(2)建立PSO-ELM神经网络拓扑结构。包括确定输入层、隐含层、输出层的神经元个数即粒子维数和选择激活函数为sigmoid。
(3)产生种群。该种群由极限学习机的输入权值矩阵ω和隐含层偏置阙值b组成,初始化粒子位置和粒子速度,根据权值和阈值的范围设置粒子速度和位置的寻优范围。
(4)得到最优参数。根据PSO-ELM模型对重构后的时序序列进行训练,以获得最佳的模型参数,主要包括,最大迭代次数T=500、种群数量M=30、学习因子c1=c2=2、r1和r2为两个随机产生的参数,范围为(0,1),粒子维数D等。
(5)确定以极限学习机训练集的均方根误差作为适应度值函数,计算出每个粒子的适应度值,求出每个粒子的个体极值和全局极值。
(6)通过比较,不断更新粒子的速度和位置[19]。
(7)判断是否达到最大迭代次数或者最小误差,若达到,则停止迭代;若没达到,转到步骤5,继续迭代。
1.4 伪近邻法原理

(10)
则Ym(n(i,m))为Ym(i)的虚假邻近点,对于实际工程中的时序序列,取Rt为[10,50]之间的某一数值[18],当m从1开始时,计算出此时虚假邻近点所占的比例大小。然后将m的值逐渐增加,当其中的虚假邻近点所占的比例低于5%,或者是虚假邻近点的比例不随着m的增加而降低时,可以认为此时吸引子的结构被完全打开,此时的m即为嵌入维数。
2 基坑变形的EMD-PSO-ELM的预测方法
本文将EMD算法与粒子群优化后的极限学习机算法结合在一起,建立EMD-PSO-ELM预测深基坑变形的动态时序序列模型,模型的工作流程如图1所示。
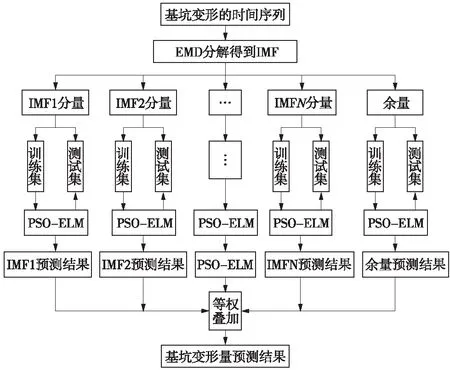
图1 EMD-PSO-ELM预测步骤流程
若深基坑变形的时序序列为U(t)(t=1,2,…,N),预测变形的基本过程如下。
(1)用EMD算法将监测的基坑变形量时序序列进行分解,获得n个本征模态函数(IMF)分量Ci(t)(t=1,2,…,N)和一个余量rn。
(2)将分解出的若干IMF分量和余量分成训练集和测试集两部分,对PSO-ELM模型进行初始化,选择适当的参数。采用伪近邻法将得到的分量和余量进行相空间重构,利用PSO-ELM预测模型对空间重构后的训练集进行学习,以获得模型的最优参数。利用经过学习之后的PSO-ELM预测模型对分解出的各分量测试集进行预测。
(3)将经过PSO-ELM模型预测后的数据利用等权求和的方法进行叠加,获得最终基坑时序序列变形量的预测结果。
3 工程算例
3.1 实验数据的获取及分析
将EMD-PSO-ELM组合模型应用于南宁某地铁车站深基坑变形预测中,车站明挖站厅基坑设计开挖长度为82.4 m,基坑开挖宽度41.8 m,标准段基坑底部埋深约24.35 m。基坑南侧和东侧的围护结构体系采用两种钻孔灌注桩,分别为φ1 500@1 700 mm和φ1 200@1 500 mm,钻孔灌注桩桩长均为35 m,基坑的北侧和西侧围护结构采用φ1 200@1 500 mm钻孔灌注桩,桩长分别为40 m和35 m,在竖直方向采用了4道支撑体系,均为钢筋混凝土支撑。此基坑工程地下分布有广泛的粉砂岩、泥质粉砂岩以及粉细砂岩等对基坑的变形极易产生不利影响,且该基坑附近有较多的小区、商业区,为确保基坑的安全施工,在施工过程中对基坑的变形进行了监测,基坑监测点如图2所示。

图2 基坑监测平面
本次训练集样本共选取J7监测点2016.4.25-2016.7.7的基坑变形原始监测数据进行分析和预测,基坑的变形如图3所示。

图3 基坑变形监测曲线
从图3可以看出基坑在开挖与支护的过程中变形并非是平稳的线性变化,而是伴随基坑施工波动性变化。基坑的变形属于非平稳的时序序列,造成非平稳现象的主要原因有:自然因素、施工因素、支护结构设计因素。利用EMD算法将基坑变形的原始监测数据进行分解,把原始时序序列中的高频和低频信息量进行逐级分离,有效地分解成相对平稳的分量。分解结果如图4所示。

图4 EMD的多尺度分解结果
由图4可以看出,基坑变形时序序列具有明显的多尺度特征。4个IMF分量按照从高频到低频的顺序排列,呈现出来了不同维度的波动信息。其中,IMF1属于高频分量,体现了基坑变形时序序列中的噪声信息,造成此种波动的原因主要有外界环境、测量仪器产生的误差等;IMF2、IMF3属于中频分量,其波动程度较大,造成此种现象的主要原因有施工工序、基坑支护方案的选取、地质条件、时空作用等的影响;IMF4和R属于低频分量,其中R为残余分量,其变化较为平稳,体现除了基坑的变形趋势,可以从本质上反映基坑变形的本质特征。基坑的监测数据经过经验模态(EMD)分解,可以从各种不同的层面对基坑的时序序列进行分析,同时可以消除原始信号中高频频率带来的噪声信息,从而得到基坑变形的本质信息,反应基坑变形的本质特征。
进行相空间重构时采取伪近邻法获得相空间的嵌入维数m,对分解出来的各维度IMF分量和余量进行空间重构,嵌入维数如表1所示,然后得到重构之后的基坑每日变形数据,利用其对基坑变形量做出相对应的分析和预测,最后采取等权求和的方法获得最终基坑变形量的预测结果。

表1 空间重构参数
3.2 预测结果的对比分析
为了验证分析本文提出的模型适用性和可行性,将空间重构后的时序变形数据分为两组A和B。取A组前30 d的时序变形数据作为训练集,对PSO-ELM网络模型进行训练,将后15 d的重构数据利用训练后的预测模型对时序变形量作出相对应的预测,同时B组后15 d的监测数据作为验证集,将测试集预测结果与验证集进行对比分析,最终结果如图5所示。

图5 基于EMD-PSO-ELM的基坑变形量预测
为验证经验模态分解(EMD)应用于基坑变形非线性时序序列的优越性,将经过训练后的PSO-ELM模型用来预测验证集的基坑变形量,预测结果如图6所示。

图6 基于PSO-ELM的基坑变形量预测
将两种模型的最终预测结果进行对比分析,由图5和图6可知,未经EMD算法分解的PSO-ELM预测模型在预测基坑非线性、非平稳条件下的变形量时有着较大的误差;而EMD-PSO-ELM预测模型经过EMD算法分解后将基坑变形的监测数据分解为多个不同维度的平稳序列,然后利用PSO-ELM模型对各维度分量进行预测,结果和现场的监测值有着较好的统一性,EMD-PSO-ELM预测模型对非线性基坑变形量的预测有着很好的适用性。
以结果的相对误差值为评价指标来验证模型的优越性,结果如表2可知,PSO-ELM预测模型相对误差为0.31%~0.75%,平均相对误差为0.64%,其预测精度在实际工程应用中尚有不足;EMD-PSO-ELM预测模型的相对误差为0.22%~0.42%,其平均相对误差为0.32%。由此可得出,EMD算法从数据时序序列本身挖掘其内在的隐藏规律,进一步提高了预测模型的精度,对于非平稳变化时序序列有很好的适应性。

表2 两种模型误差分析 %
从总体结果来看,基坑变形预测结果与实际监测值有着高度的一致性,这表明该预测方法可以较好地应用于基坑变形的预测工作中,同时该预测结果可以进一步对施工过程中的基坑非线性变形做出预警,从而保证了基坑在周围建筑环境复杂的地区开挖的安全进行。
4 结论
(1)由于基坑的变形受到场地条件、地质条件、施工工序等的影响,使得基坑的变形量呈现出了非平稳、非线性的时序序列。采用EMD算法可以将原始的时序序列分解成多维度体现基坑变形的波动性和变形趋势的IMF分量,从多维度反映了基坑变形的本质,进一步提高了基坑预测模型的精度。
(2)本文将EMD算法和PSO-ELM模型相结合,不仅降低了环境因素、时空效应等非平稳因素对于基坑变形的影响,还降低了人为主观因素对于模型参数选取的误差。运用EMD的方法将基坑变形的原始时序序列分解成4个IMF分量和1个残余分量。利用PSO-ELM模型对于基坑变形量进行预测,然后将得到的各预测值根据等权求和的方法进行叠加,进而得到最终的预测结果。同时以相对误差作为评价模型的基本指标,对模型的精度进行检验,结果表明EMD-PSO-ELM预测模型对于基坑变形的预测结果与实际监测值有着较好的一致性,且平均相对误差仅为0.32%,其预测结果的精度比未进行EMD算法分解的模型有着明显的提高。
(3)EMD-PSO-ELM的时序序列预测模型从本质上诠释基坑变形量非平稳性的特征,从深层次挖掘出了基坑变形的规律,降低了外界非平稳因素对预测模型结果的影响,实现了对于基坑非平稳变形的动态预测,为分析基坑非稳定特性提供了理论依据。
