页岩气井井下安全阀完整性研究*
2020-09-04赵苑瑾
张 智,赵苑瑾,吴 优,邓 虎,卢 齐
(1.西南石油大学,油气藏地质及开发工程国家重点实验室 四川 成都 610500; 2.中国石油川庆钻探工程有限公司钻采工程技术研究院 四川 广汉 618300)
0 引 言
根据联合国贸易和发展会议在2018年5月发布的一份报告显示,中国的页岩气储量排名全球第一(达31.6×1012m3),技术可采资源量仅次美国排名全球第二(达4.74×1012m3)。而在2019年,四川盆地长宁—威远和太阳区块的页岩气累积探明量为10 610.30×108m3,形成了四川盆地万亿方页岩气大气区。因此,中国的页岩气开采潜力巨大,国家也出台了一系列政策加大对页岩气的开采力度,根据《中国页岩气发展规划(2016—2020年)》公布的数据,2020年我国将力争实现页岩气产量300×108m3[1]。截止2019年,中国石油西南油气田的页岩气井泸203井日产量达到了137.9×104m3,成为国内首口单井测试日产量超百万立方米的页岩气井。但页岩气井产量的增加也引起了一系列的问题与挑战,如井口装置失效、套管变形等,对人身安全、经济发展和环境保护造成了严重威胁[2-3]。而井下安全阀作为井筒屏障单元之一,能够迅速自动关闭,阻止地层流体向地面无控制的泄流,因此高产页岩气井都应该安装井下安全阀。
但井下安全阀也会给页岩气井的生产带来一定风险,因此有必要对其进行风险评价和完整性管理,以保证页岩气的安全生产。目前,国内外学者对井下安全阀的风险评价进行了大量研究,如李建宏等[4]从井下安全阀弹簧的失效、操作条件、履历和管理水平4个方面对某油田井下安全阀进行了风险评估;刘益维等[5]基于马尔可夫模型,参考OREDA数据,对地面控制型井下安全阀进行了可靠性评估,确定了系统检修周期;Marvin Rausand等[6]分别建立了井下安全阀寿命的指数分布模型和威尔逊分布模型,讨论了井下安全阀作为防止井喷发生的安全屏障的可行性,讨论了平衡风险和运营成本的策略;J .M. Busch等[7]分析了Kuparuk地区井下安全阀完井与无井下安全阀完井井喷风险的大小,明确了油气井风险值与井下安全阀寿命的关系,为井下安全阀的使用提供了参考。然而,井下安全阀风险评估的复杂性和风险因素间的相关性等特点导致上述评估方法存在一定的局限性,由于部分难以定量的风险因素往往通过定性描述进行打分赋值,评价结果存在较大的主观随意性和模糊性。而贝叶斯网络可以表达及分析不确定事件,从模糊信息中实现学习与推理,是不确定性分析领域最有效的理论模型之一,但是贝叶斯网络模型中的条件概率往往依赖于专家知识及大量的统计数据,目前,在井下安全阀风险评估中,大多数区块并未建立完备的风险案例库,无法提供可靠的统计数据。因此需要结合模型,简化条件概率的计算,近似确定贝叶斯网络的条件概率参数[8-10]。
为此,建立了一套页岩气气井井下安全阀的风险评价方法,实现了井下安全阀的风险评价与管理。
1 页岩气井井下安全阀风险评价流程
页岩气井井下安全阀风险评价流程,如图1所示。首先通过故障树分析法系统地识别了页岩气井井下安全阀失效的主要形式和关键影响因素,再由贝叶斯网络结合Noisy-OR gate模型计算了井下安全阀的失效概率,并基于国际通用标准量化井下安全阀不同失效形式的影响程度,最后结合Sintef统计数据,计算失效形式的权重,得到井下安全阀风险值,确定其风险等级。
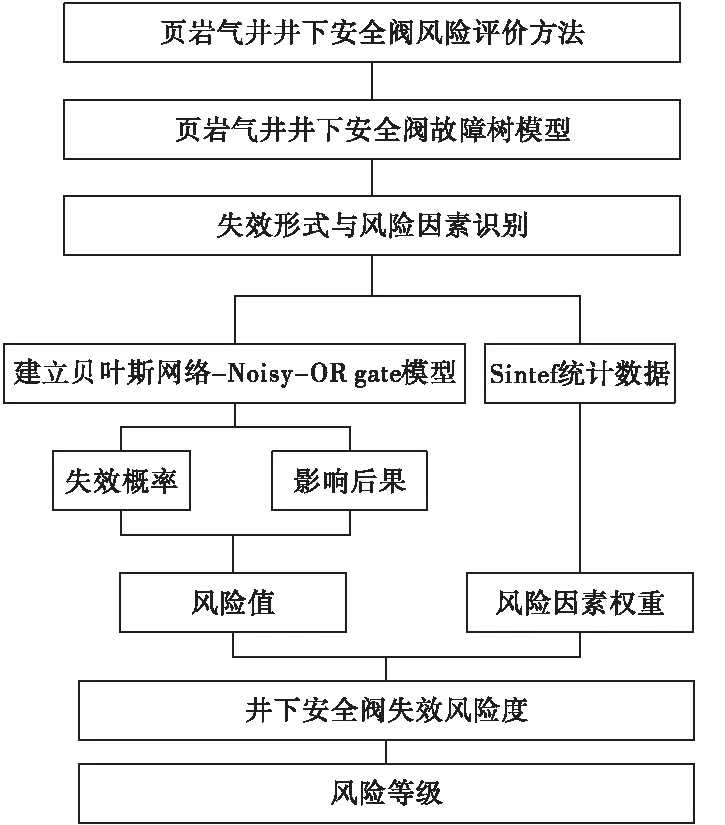
图1 页岩气井井下安全阀风险评价流程
2 页岩气井井下安全阀失效主控因素分析
目前较常用的是地面控制油管回收式井下安全阀,通常由地面液压系统、活塞运动部分、动力弹簧部分、阀板开关部分组成,其结构如图2所示。
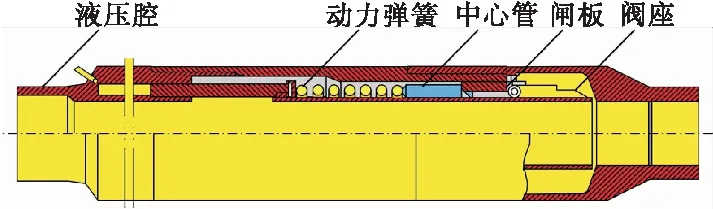
图2 井下安全阀结构图
通过分析以往井下安全阀失效的案例,结合OREDA标准和页岩气井特点,将井下安全阀失效分为2种类型:关键性失效及非关键性失效[11]。
2.1 关键性失效
井下安全阀发生关键性失效时,无法发挥井筒屏障单元的功能,同时只能在测试期间进行检测,影响后果严重,主要表现为密封泄漏及关闭失败。
1)密封泄漏(LCP,Leakage in Closed Position) 当阀门密封处的泄漏量超过了API RP 14B中的规定值时,就认为井下安全阀发生了密封泄漏。密封泄漏的影响因素较多,主要有阀体、阀座受损、不规范的电缆作业、腐蚀等。由于油气井生产过程中,井下安全阀通常都是打开状态,因此,只有在关闭井下安全阀,对其进行测试时,才能判断是否发生密封泄漏。
2)关闭失败(FTC,Fail to Close) 关闭失败是井下安全阀失效形式中最危险的一种,使井下安全阀完全失去阻止地层流体向地面无控制流动的能力。通常由地面控制管线堵塞,阀体、阀座受损,腐蚀等因素影响。同密封泄漏一样,井下安全阀关闭失败也无法被立即检测。
2.2 非关键性失效
当井下安全阀发生非关键性失效时,只是对生产造成了影响,仍能发挥井筒屏障单元的屏障作用,而且能立即被发现,因此给油气井正常生产带来的风险较小。
1)打开失败(FTO,Failure to Open) 打开失败是指井下安全阀关闭后,无法打开。通常是由地面控制系统出现故障引起的,发生后能立即被检测。
2)提前关闭(PC,Premature Closure) 当地面液压控制管线发生泄漏或阀体密封失效时,井下安全阀会提前关闭,导致生产立即停止,发生后也能立即被检测。
根据井下安全阀失效影响因素的逻辑关系建立其故障树模型,如图3所示。

X1-材料本身缺陷;X2-安装时操作不当;X3-密封面损伤或有附着物;X4-弹簧失效;X5-防腐措施失效;X6-材料抗腐蚀性能失效;X7-腐蚀环境;X8-活塞失效;X9-地面管线破裂;X10-地面管线堵塞;C1-阀体、阀座受损;C2-腐蚀;C3-地面控制单元失效;B1-密封泄漏;B2-关闭失败;B3-打开失败;B4-提前关闭;A1-关键性失效;A2-非关键性失效;T-安全阀失效图3 页岩气井井下安全阀失效故障树图
3 井下安全阀失效风险值计算
在风险评估中,通常将某种失效形式的发生概率Pi与失效所造成损失的影响程度Si用风险值Li来综合度量,该失效形式的风险值可由式(1)得到[12]。
Li=Pi×Si
(1)
由图3可知,井下安全阀有2类失效形式,因此其综合风险值R为:
(2)
式中,ωi为失效形式的权重,无量纲。
为了便于实际使用,将综合风险值R分为4级,并制定相应的管理措施,见表1[13]。

表1 井下安全阀风险等级
3.1 失效概率分析
参考国内外相关文献,井下安全阀的影响因素中腐蚀失效(C2)及弹簧失效(X4)具有时间效应,可由对应的数学模型进行量化,其他因素可根据现场统计数据或专家经验得到。
1)腐蚀失效 采用国际上通用的幂函数模型计算,见式(3),通过该模型计算出腐蚀速率后,可根据腐蚀速率的大小预测腐蚀失效的发生概率[14-15]。
ν=atb
(3)
式中,ν为腐蚀速率,mm/a;t为服役时间,d;a为试样暴露在初期腐蚀环境的腐蚀量;b为腐蚀产物保护性系数,无量纲。
2)弹簧失效 油井在正常生产时,井下安全阀始终处于打开状态,因此,由开关阀门引起的动载荷以及阀杆倾斜引起的非中心载荷均为0,只需考虑静载荷的影响,其计算公式见式(4),可知随时间增加,弹簧钢丝由于腐蚀,直径减小,导致弹簧所受实际剪切应力增大,更容易发生失效。通过比较弹簧的实际剪切应力与抗剪切强度的大小,可以推测弹簧失效概率。
(4)
式中,τ为剪切应力,MPa;F为轴向载荷,kN;D为弹簧中径,mm;d为弹簧钢丝初始直径,mm。
3.2 失效影响程度计算
对于影响程度,本文主要考虑了井下安全阀失效对人员、财产、环境的危害性以及现场的监测、应急能力这4个方面,并参考相关标准及文献进行了量化,以综合损失系数S来代表井下安全阀失效的影响程度,见式(5)所示。
S=(S1+S2+S3)×S4
(5)
式中,S1为人员损伤系数,无量纲;S2为经济损失系数,无量纲;S3为环境影响系数,无量纲;S4为监测和应急能力,无量纲。
S1、S2、S3、S4的量化指标见表2和表3[16]。

表2 S1、S2、S3的量化指标

表3 S4的量化指标
4 井下安全阀的贝叶斯网络和Noisy-OR gate模型
4.1 贝叶斯网络
贝叶斯网络是一种基于概率分析的现代不确定性推理方法,不仅利用样本信息,还考虑了参数的先验信息,适用于缺乏统计数据的概率计算,其数学表达式为B=(G,P),通常由有向无环图(Directed Acyclic Graph, DAG)与条件概率表(Condition Probability Table,CPT)两部分组成[17]。
根据故障树图与贝叶斯网络的对应关系,可将图3转换为20个节点组成的有向无环图,如图4所示,箭头代表了节点间的因果关系,通常由父节点(原因)指向子节点(结果)。父节点与子节点之间不是相互独立的,存在条件概率,体现了各节点之间的影响程度,通常任意节点Xi的先验概率由符号Pi表示,代表凭经验判断的节点Xi概率,CPT由符号P(Xi|π(Xi))表示,其中π(Xi)代表节点Xi的父节点集合。则包含n个变量(X1,X2,…,Xn)的联合概率分布P(X1,X2,…,Xn)可表示为[18]:
(6)
上式将联合概率分布的计算转化为条件概率乘积的形式,大大降低了贝叶斯网络模型的计算和推理过程。同时由于节点属于离散型变量,只存在两种状态:失效或正常工作,因此对于有n个父节点的节点Xi,其CPT的确定需要2n项条件概率和先验概率值,难以在实际生产中应用。因此,笔者引入Noisy-OR gate模型简化贝叶斯模型。
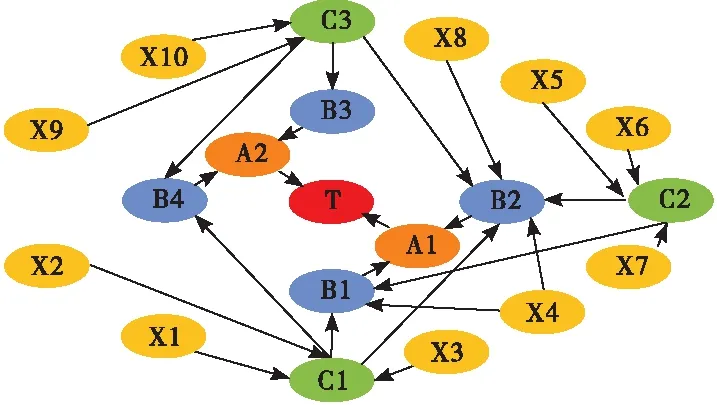
图4 井下安全阀的贝叶斯网络模型
4.2 Noisy-OR gate模型
图5所示为一典型的Noisy-OR gate模型,图5中每个父节点是条件独立的,每个变量仅有2种状态,为一典型的Noisy-OR gate模型,节点C有n个条件独立的父节点B1,B2,…,Bn,每个变量仅有两种状态,发生失效由真值1表示,正常工作由0表示,由π(C)代表节点C的父节点集合,其子集定为π(C)sub,由于各父节点独立的影响子节点C,父节点之间的连接关系为逻辑“或”,因此π(C)sub取真值时,节点C取真值的概率为:
(7)
实际上,除了列出的n个因素会影响节点C的发生外,还存在一些未知因素的影响,此时应采用Noisy-OR gate模型的扩展模型Leakage Noisy-OR gate模型,将这些未知因素视作一个父节点BL,如图6所示,其概率设为PL,加入模型中,则Leakage Noisy-OR gate模型中节点C取真值的概率为[19]:
(8)
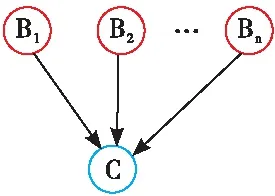
图5 典型Noisy-OR gate模型
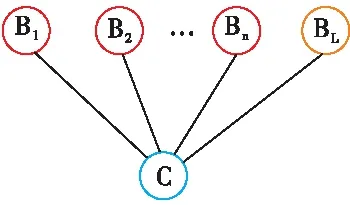
图6 典型Leakage Noisy-OR gate模型
此外,通过Leakage Noisy-OR gate模型还可以求解父节点与子节点的连接概率。将子节点C的父节点看作某一父节点Bi及除Bi外的全部父节点集合Ba,对应的概率分别为Pi及Pa,Pa中的事件总能导致子节点C发生,即Pa总为真值,由式(7)可得:
P(C=1|Bi)=1-(1-Pi)×(1-Pa)
(9)
(10)
因此父节点Bi的连接概率Pi为:
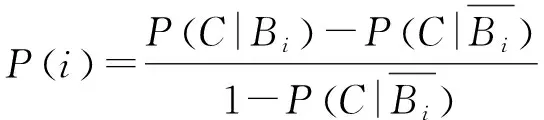
(11)
5 实例计算
5.1 井下安全阀初期失效概率
对于网络中父节点的条件概率,可以通过历史统计数据得到,或者在没有足够多的样本可供学习的情况下,可以先通过专家经验知识及相关文献标准等进行主观量化,随着生产的进行,有关井下安全阀失效的数据逐渐增加,将其导入模型中,利用贝叶斯网络的自主学习能力,提高原始模型的准确度。
四川盆地某高产页岩气井井下安全阀的阀体、阀座受损(C1)的父节点条件概率分别为:P(C=1|X1=1)=0.90,P(C=1|X2=1)=0.70,P(C=1|X3=1)=0.70,P(C=1|X1=0)=0.75,P(C=1|X2=0)=0.55,P(C=1|X3=0)=0.50。可由式(6)计算X1、X2、X3的连接概率分别为:0.60,0.33,0.40。同时考虑未知因素的影响,假设PL=0.05,由式(8)可计算节点C1的条件概率表,见表4。

表4 节点阀体、阀座受损(C1)的条件概率表
同理,可以计算其他节点的条件概率表。因为阀体、阀座受损(C1)、腐蚀(C2)、地面控制单元失效(C3)、弹簧失效(X4)、活塞失效(X8)发生必然导致井下安全阀失效,因此它们相对于井下安全阀的连接概率为1,未知因素的连接概率仍假设为PL=0.05,则可以确定计算井下安全阀失效的条件概率参数,由于该气井初期一切设备完好,操作、管理人员定期接受培训,因此除了腐蚀环境(X7)以外的根节点失效概率很小,定为0.05,将参数输入贝叶斯网络模拟软件GeNIe2.0,计算井下安全阀初期失效概率,如图7所示。可知在该先验条件下,井下安全阀失效的概率为26%,关键性失效概率为23%,非关键性失效概率为16%。
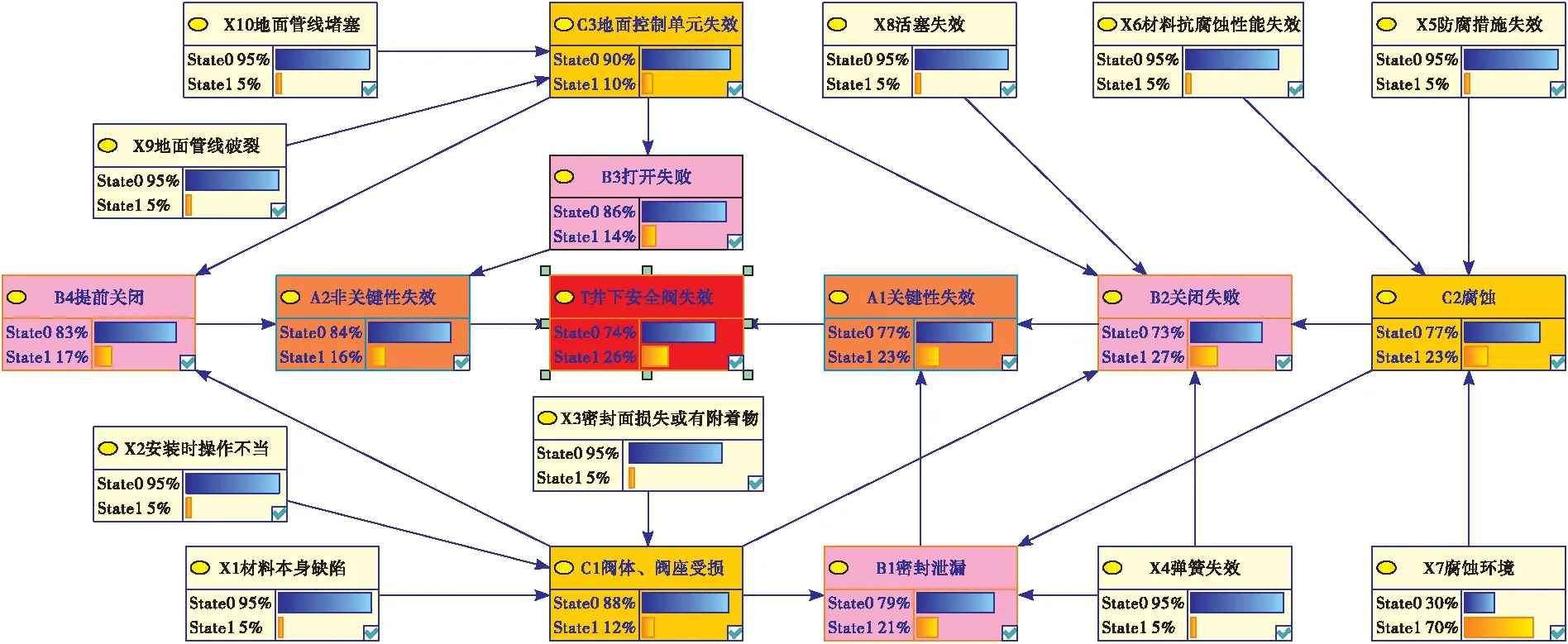
图7 基于贝叶斯网络的井下安全阀初期失效概率
当该井下安全阀发生非关键性失效时,仅对生产有轻微影响,其人员损失系数、环境污染系数均为0,经济损失系数为2,且能被及时处理,应急、处理能力系数为75%,即其影响程度系数为0.15。当该井下安全阀发生关键性失效时,井下安全阀无法作为井筒屏障单元阻挡流体的泄流,人员损失系数、环境污染系数、经济损失系数、应急处理能力系数分别为3、3、5、50%,即其影响程度系数为5.5。由式(5)可得到非关键性失效的风险值为0.09,关键性失效的风险值为4.35,该井的2种失效形式的统计数据参考Sintef井下安全阀失效数据,见表5,可知非关键性失效的权重为0.34,关键性失效的权重为0.66。

表5 Sintef关于井下安全阀失效的统计数据
因此,由式(9)可得该页岩气井初期井下安全阀的风险值为0.84,属于低风险,只需采取监测措施。
5.2 预测井下安全阀失效概率随时间的变化
在井下安全阀的整个服役寿命期间,并非所有根节点的发生概率都会发生变化,比如材料本身缺陷(X1)、操作、安装不当(X2)等,失效概率变化的是具有时间效应的节点:弹簧失效(X4)及腐蚀(C2)。因此,以1年为时间间隔,将失效概率发生改变的量输入模型中,预测15年内井下安全阀的失效概率变化情况,如图8所示。
由图8可知,井下安全阀刚安装时,失效概率较低,为26%,随着生产进行,失效概率迅速增加,第4年达到了73%,随后缓慢增加至90%后,不再发生变化。因此,该高产气井的井下安全阀检验周期应不超过3年,最好一年检测一次,这也符合标准所规定的高含硫气井检验周期。
该高产气井井下安全阀已服役4 a,将这4 a的现场统计数据与贝叶斯网络计算数据进行对比,见表6。
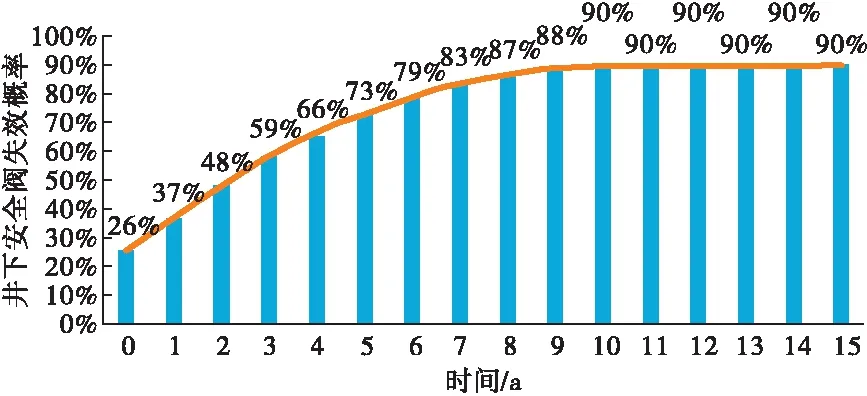
图8 井下安全阀失效概率预测值
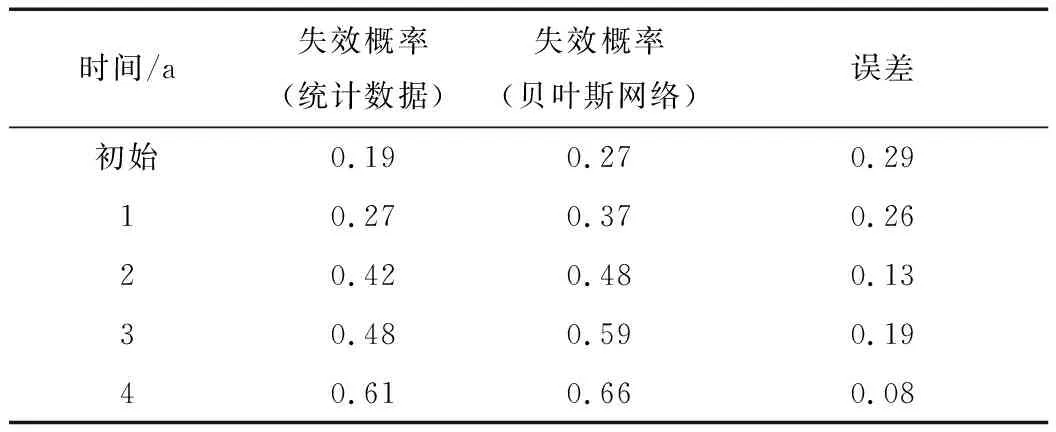
表6 井下安全阀失效的实测数据与计算数据误差分析
由表6可知,由贝叶斯网络计算所得的井下安全阀失效概率与现场实测数据较为符合,误差在工程允许误差范围内,初始失效概率误差较大是因为初始数据主观性较强,缺乏现场数据修正,而随着生产的进行,将生产数据加入贝叶斯网络模型中,利用其学习能力,计算结果逐渐向实际靠拢。因此,井下安全阀的贝叶斯网络模型能有效指导生产,其失效预测较为可信。
5.3 失效关键影响因素分析
井下安全阀的失效因素众多,对其影响的程度各不相同,为了更加有效地管控井下安全阀风险,可将建立的贝叶斯网络模型中T井下安全阀的发生概率设为100%,利用贝叶斯网络的反向推理,即可得到井下安全阀的关键影响因素,如图9所示。
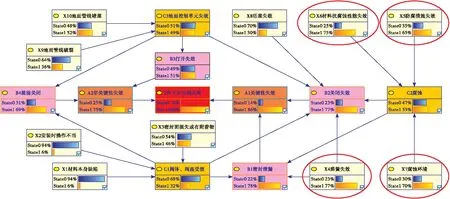
图9 井下安全阀失效主要影响因素分析
将图9中各影响因素的失效概率与正常工作概率绘制为柱状图,如图10所示,进行比较,可知主要影响因素为弹簧失效(X4)、防腐措施失效(X5)、材料抗腐蚀能力(X6)、腐蚀环境(X7),因此在生产中应重点关注这几个因素。
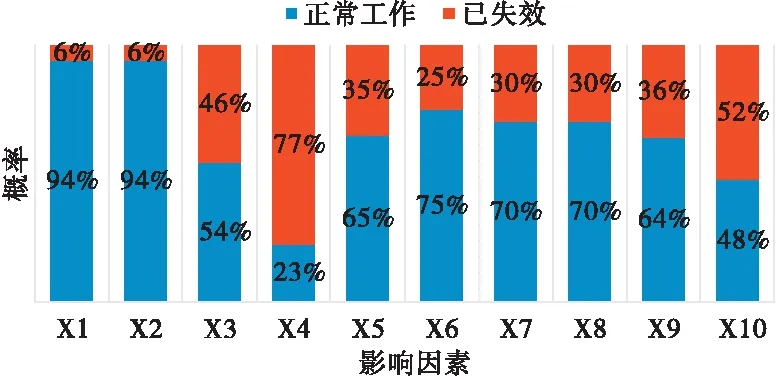
图10 井下安全阀的关键影响因素识别
6 结 论
1)以失效后井下安全阀能否发挥井筒屏障的功能,将井下安全阀失效分为了关键性失效和非关键性失效2类,并通过故障树分析法得到了井下安全阀的主要影响因素。
2)贝叶斯网络模型结合Leakage Noisy-OR gate模型简化了井下安全阀风险评估的计算过程,降低了主观因素的影响。计算结果表明,实例中井下安全阀失效影响最大的是腐蚀环境、弹簧失效、材料防腐性能、防腐措施失效,现场工作人员应加强对这四方面的监控管理。
3)井下安全阀的风险评估中涉及众多影响因素,对这些影响因素量化或定级需要收集大量的资料,尤其需要获得可靠的现场统计数据,需在今后的工程实践中逐步完成。
