基于高速SerDes中非等值尾电流源技术的新型高线性度相位插值器设计
2020-09-04郭凯乐王和明陆德超
郭凯乐,王和明,刘 涛,陆德超
(空军工程大学防空反导学院,西安, 710051)
高速串行接口(Serializer and Deserializer,SerDes)作为芯片间、背板间、机柜间和系统间的高速数据传输核心模块,其性能已经成为制约现代电子信息系统发展的关键因素[1-2]。时钟数据恢复电路(Clock and Data Recovery, CDR)作为高速串行接口中接收端同步数据的核心模块,其恢复时钟的抖动性能直接影响SerDes的误码率[3-4]。相比于模拟锁相环型CDR,相位插值器(Phase Interpolator,PI)型CDR采用数字滤波器和数字码实现时钟相位控制,在芯片面积、功耗和工艺易移植方面有非常大的优势,因此得到广泛应用[5-7]。然而PI型CDR最大的挑战是PI输入控制码和输出相位关系的线性度,它的性能会直接影响CDR的恢复时钟的抖动性能,进而影响误码率[8-9]。文献[10]采用了传统等值尾电流源阵列的相位插值器,其数学模型上固有的非线性因素导致相位插值器调节精度较低,恢复时钟的抖动较大。为了解决该线性度问题,文献[11]采用2个对称的相位插值器,对其输出进行平均来提升输出相位的线性度,但双相位插值器结构增加了电路的功耗、面积以及设计的复杂度。文献[12]采用8个相位间隔为45°的时钟,经4个相位选择器后输入2个相同的相位插值器,不仅结构复杂,且时钟信号时序紧张,不适用于高速CDR。
本文设计了一种新型非等值电流源的相位插值器,在研究传统相位插值器非线性产生机理的基础上,根据相位插值器输出时钟相位与尾电流源权重的反函数关系,计算出尾电流源阵列中每个电流源的精确设计比例,有效提高了控制信号与输出时钟相位的线性度。该技术克服了传统等值电流源相位插值器理论上固有的非线性因素,采用一个相位插值器,避免了双插值器设计的高功耗结构,采用2对正交的差分信号,最大程度上缓解了时序紧张问题,是一种非常适合高速CDR的高线性度相位插值器。
1 非等值电流源相位插值型CDR接收机系统架构
图1给出了本文设计的PI型CDR接收机系统架构。该CDR接收机采用1/4速率架构,主要包括相位插值器、采样器和相位追踪控制电路。为了降低系统功耗,CDR的高频部分采用CML电路设计,相位追踪控制电路采用标准的CMOS数字电路实现。该CDR的工作过程如下:本地时钟经1/2分频器后输出I、Q 2路正交的差分信号IP、IN和QP、QN,经相位插值器插值后生成IP*、IN*和QP*、QN*,产生八相采样时钟,8个时域交织采样器利用这八相1/4速率时钟,对输入的高速数据进行采样,得到4路数据信息流和4路沿信息流。受到数字电路运行速度的限制,将这8路信息流经分接器降速,得到32路对齐的信息流[13]。通过鉴相,得到16个超前/滞后/保持信号,送入滤波器。将滤波器输出的高7位通过编码器产生相位控制码,经相位插值器对应调整八相时钟的采样位置,使得数据采样沿位于数据位的中间,保证最佳采样[14]。

图1 PI型CDR接收机系统架构
2 相位插值器的理论分析
2.1 相位插值器的原理
相位插值器是PI型CDR中的关键模块,其输入控制码和输出时钟相位关系的线性度会直接影响CDR的动态特征,当输入数据与本地时钟存在频率差时,会影响它的时钟抖动[15-18]。因此,高线性度的相位插值器的设计是高性能PI型CDR的关键因素之一。
相位插值器最重要的特征是单调、线性的传输特性。从理论上讲,相位插值器的输出相位应与输入控制码呈一次线性函数关系:
φout=kPIn(0≤n≤N,0≤φout≤2π)
(1)
式中:kPI为相位插值器的增益;n为控制码。式(1)表明,当n从0增加到N,输出相位从0增加到2π,若kPI保持不变,则φout与n的关系曲线就是单调线性的。
由于2个非线性相关的向量可以张成整个平面,因此2个非线性相关的输入时钟信号c1和c2合成时钟的相位就可遍历0到2π。设c1=sin(ωt),c2=sin(ωt+φd),其中ω是输入时钟的角频率,φd是输入时钟的相位差,c1的相位为0。c1和c2的权重系数分别为A1和A2。相位插值器通过输入时钟在不同权重下的线性组合来输出不同相位的时钟,从而实现相位插值的功能[7]。相位插值器的输出信号可以表示为:
Vout=A1sin (ωt)+A2sin (ωt+φd)
(2)
将0到2π分为4个象限,每个象限关系等价,因此选择第一象限进行分析,A1,A2满足:A1+A2=1,0<(A1,A2)<1[15]。令a=A1+A2cosφd,b=A2sin (φd),则式(2)可改为:
(3)
由式(3)可知输出的相位和幅度是由A1、A2和φd决定的。其中:
(4)
(5)
文献[19~22]表明,90°相位差可以实现PI复杂度和线性度的折中,因此取φd为π/2,则式(4)和式(5)可以改写为:
(6)
(7)
由式(7)可知,PI输出时钟的相位是A1、A2的反三角函数。
2.2 传统等值电流源型相位插值器
图2为传统等值电流源型相位插值器结构,输入晶体管M1、M2、M3、M4的尺寸均相同,负载R1、R2相等,且等于R,输入信号为2对正交的差分信号VIP、VQP、VIN、VQN,其相位分别为0°、90°、180°、270°。相位插值器对这2对时钟进行相位插值,可得到相位介于二者之间的恢复时钟[16]。通过改变这2个差动对的尾电流可以调整恢复时钟的相位[17]。
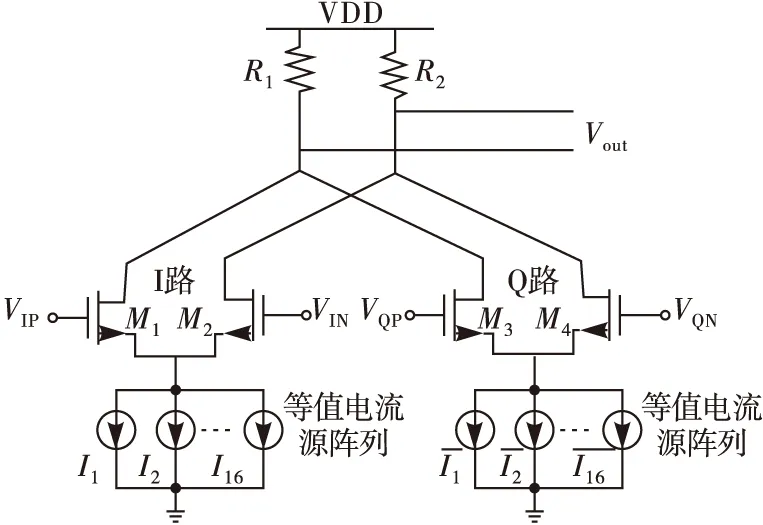
图2 传统等值电流源型相位插值器结构
由图2可得输出电压:
Vout=AvIVIP+AvQVQP
(8)
由半边电路法可求得:
(9)
(10)
联立式(7)(9)(10)可得:
(11)
式中相关参数符号定义见文献[17]。
输出相位如图3所示。
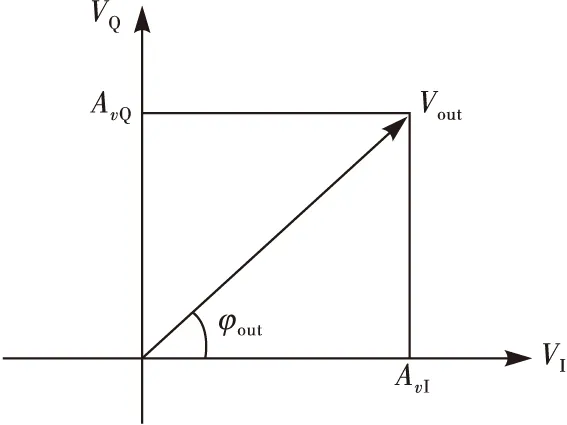
图3 输出向量示意图
由式(11)可知,φout大小仅由Q通路与I通路晶体管宽长比与电流之积平方根的比值决定,这样输出相位基本不随温度的变化而变化。这种结构的尾电流由16个等值电流源阵列组成,通过控制各支路尾电流源的比例来改变输出信号的相位,每个电流源的电流大小为:
(12)
电流源采用长沟道器件,因此式(12)中由沟道调制效应引起的λVDS部分可忽略。因为电流源的源极直接接地,因此由源极和基底之间的电压Vsb产生的体效应对VTH的影响也可忽略,而VGS由Vbias统一提供,因此式(12)中的(VGS-VTH)2部分相同。
根据上述分析可得:
(13)
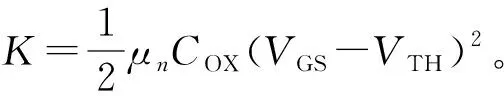
把式(13)带入式(11)可得:
(14)
式中相关符号定义见文献[10]。
对于上述的等值电流源阵列型PI,Q路尾电流源权重系数AvQ与PI温度控制码n成线性关系(AvQ=n/16)。由式(14)可得传统等值电流源阵列型PI、理想PI温度控制码n与输出相位φout之间的关系见图4。
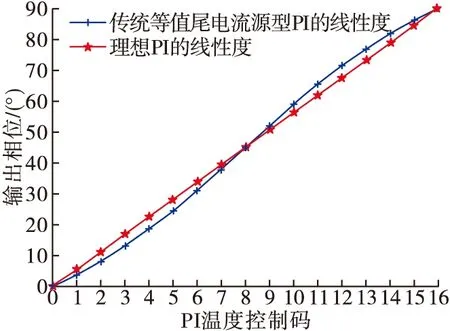
图4 PI线性度的MATLAB传真结果
由于4个象限的结果一致[6-7],因此这里只给出了第一象限中传统等值电流源阵列型PI和理想PI的n与φout之间的MATLAB仿真曲线。从数值仿真结果可知,等值电流源结构PI的线性度与理想PI线性度仍然有较大程度的偏离,而非线性问题会恶化CDR恢复时钟抖动性能,当时钟速率提高后甚至会造成严重的误码,因此要对等值电流源PI进行线性度改进,使曲线趋近于理想直线。
3 基于非等值电流源阵列的高线性度相位插值器设计
3.1 非等值电流源补偿算法
根据上述分析,对插值器的线性化改进的目的是使PI温度控制码n与输出信号相位φout呈线性控制关系,n通过改变插值器的尾电流源的权重来调节相位。若将n与AvQ的函数关系用AvQ=g(n)表示,φout与AvQ的函数关系用φout=f(AvQ)表示,则φout与n的函数关系为:
φout=f[g(n)]
(15)
因此我们的目标是找出式(15)中使φout与n呈线性函数的AvQ=g(n),并通过电路实现。因为n、AvQ、φout都是离散量,所以只要通过φout=f(AvQ)的反函数AvQ=f-1[φout]计算出0°到90°内均匀变化的16个φout值所对应的AvQ值,就可以反推出所需的非线性函数AvQ=g(n)[12]。具体实现时,保持总的尾电流源值不变,按照所得的AvQ=g(n)确定出16个电流源的具体值,便可确定电流源晶体管的尺寸。
由于Q路占总电流的比重系数为AvQ,I路占总电流的比重为AvI=1-AvQ,则式(14)改写为:
(16)
其反函数为:
(17)
把φout从0°到90°分成16等分,让φout与PI温度控制码成线性关系,可求得每个PI温度控制码对应的权重系数AvQ,如图5所示。

图5 PI温度控制码n与Q路尾电流源权重系数
3.2 非等值电流源阵列型高线性度PI电路设计
当φd=90°,N=16时,传统等值电流源结构中,每个电流源电流的大小占总电流的比例相等,均为6.25%,按照本文的算法,在保持总的尾电流值不变的情况下,根据图5计算出的权重系数,可得到每个电流源电流占总电流的比例关系以及晶体管的宽度尺寸见表1。
如图6所示,本文设计的非等值电流源阵列型相位插值器由4个差分对组成。
R1、R2为负载电阻且阻值相等,每个差分对管下面是由16个开关控制的非等值并联电流源,电流源尺寸参数按照表1设计。通过信号IG、QG、BIT 1~16控制电流源打开或关闭来确定相位插值后输出时钟的象限和相位。若将IP支路视为X轴的正半轴,则QP支路可视为Y轴的正半轴。同一时刻IP支路和IN支路、QP支路和QN支路均只有一个支路工作,选择不同的支路,就可以输出不同象限的相位,比如IN支路和QN支路工作,则相位插值器工作在第三象限,然后通过改变IP支路和QP支路的开关状态,就可以改变输出相位大小。在相位插值器工作过程中,同时只能有16个开关打开,这样就可保障相位插值器的总电流在任何状态都不会发生变化。

表1 电流源晶体管宽度取值

图6 本文非等值电流源阵列型PI电路结构
4 后端仿真结果
本文采用CMOS 65 nm工艺进行了整体电路设计,工作电压1.2 V,CDR芯片面积1.6×1.3 mm2,结构图见图7。
为了对比改进前后效果,在本地时钟为5.5 GHz时对电路进行仿真。图8(a)给出了采用传统等值电流源阵列相位插值器输出信号的眼图,图中每条曲线对应相位控制码的输出结果。输出信号过直流点的时间间隔反映其相位调整的步长。由图8(a)可知,改进前输出信号过直流点最大时间间隔为4.709 ps,与理想特性的误差为(4.709-2.84)/2.84=65.8%。
本文采用的非等值电流源阵列相位插值器仿真结果见图8(b)。改进后输出信号过直流点最大时间间隔为3.144 ps,与理想特性的误差为(3.144-2.84)/2.84=10.7%,线性度提高了55.1%。
图7 本文设计的接收机电路结构

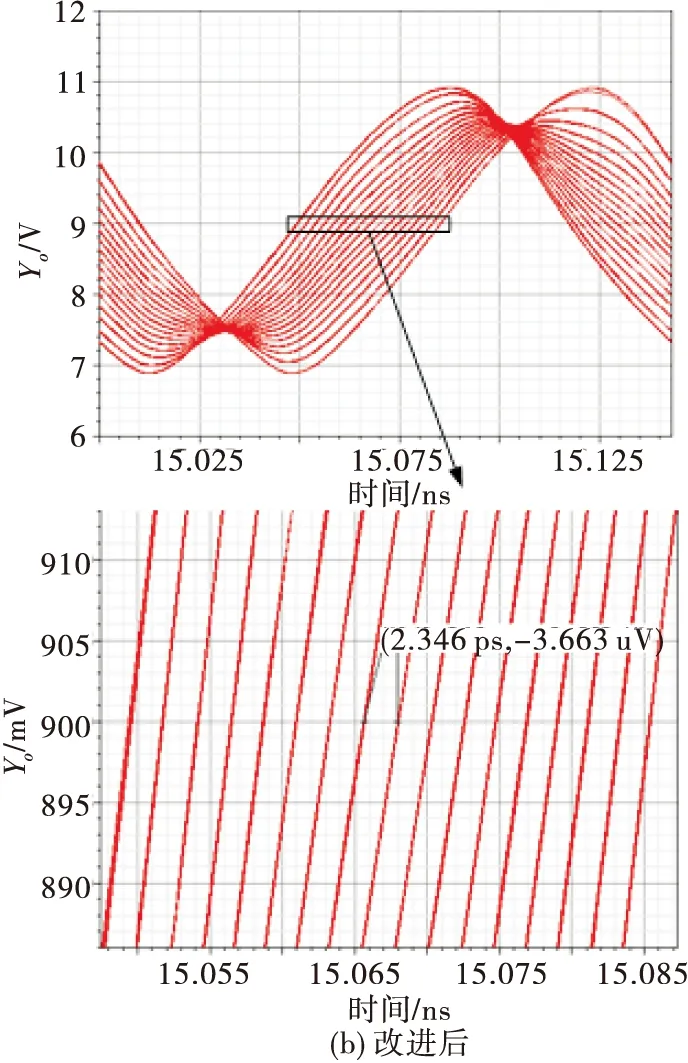
图8 改进前后PI输出时钟眼图对比
图9给出了改进前后PI的线性度曲线拟合对比。

图9 PI线性度的电路后仿结果
输出线性度决定相位插值器引入的额外抖动,是相位插值器的重要技术指标,主要通过微分非线性(Differential Non-Linearity,DNL)和积分非线性(Integral Non-Linearity,INL)来衡量。图10为PI在不同工艺角下INL和DNL与控制码的后仿曲线。由图可知,本文设计PI的DNL绝对值最大不超过0.42 LSB,INL绝对值最大不超过0.87 LSB。而传统PI的INL理论最大值为1.69 LSB[10],因此,相比于传统结构的PI,本文设计PI的线性度有了大幅提高。


图10 不同工艺角下PI的INL和DNL
本文相位插值器的参数在表2中进行了汇总,并与相关参考文献进行对比。

表2 相位插值器的性能对比
从表2中可以看出,采用本文设计的非等值电流源后,相位插值器的线性度得到了很大的提升。
考虑到版图和制程中器件的匹配度,对改进后的相位插值器进行了蒙特卡洛仿真,对尾电流管的宽度、长度、栅氧层厚度和阈值电压的失配度呈平均值为0、标准差为1的高斯分布时进行100次仿真,结果见图11。从图可以看出,相位插值器的控制码和输出相位能够保持很好的线性度,消除器件不匹配的影响。

图11 插值器线性度的蒙特卡洛仿真结果
为了进一步验证该技术,本文对22 Gb/s的接收机进行了最大频差的对比仿真验证。根据CEI标准,收发机的最大频差容限小于200 ppm,因此设定接收数据速率为22.004 4 Gb/s(与22 Gb/s数据频差为+200 ppm),本地时钟速率为5.5 GHz,仿真结果见图12,从图中可以看出,改进前时钟的抖动为8.9 ps,改进后时钟抖动为6.9 ps,恢复时钟的抖动性能提高了22.5%。
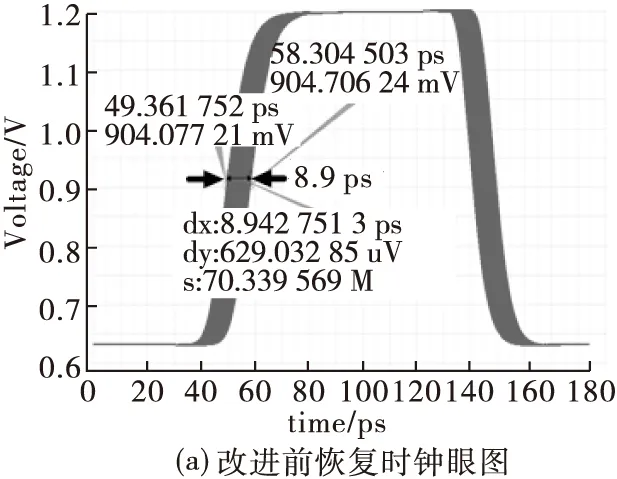

图12 改进前后PI控制码及恢复时钟抖动对比
5 结语
本文设计了一种基于非等值电流源阵列技术的高线性度相位插值器。该技术在分析相位插值器输入控制码和输出相位插值器产生非线性机理的基础上,通过计算相位插值器输出时钟相位与尾电流源权重的反函数关系,精确设计了相位插值器中尾电流源阵列参数,实现了高速率下相位插值器的高线性度关系,有效提高了相位插值器的线性度。采用65 nm CMOS工艺设计了一款基于本文线性相位插值器的22 Gb/s SerDes接收机。仿真结果表明:传统等值电流源结构相位插值器的最大相位误差为65.8%,本文设计的线性相位插值器的最大相位误差仅为10.7%,线性度提高了55.1%;CDR恢复出的时钟抖动从8.9 ps降低到6.9 ps,抖动性能提高了22.5%。
