数控车床宏程序编程加工非圆曲线(椭圆)案例分析
2020-09-03潘熠如
潘熠如

摘 要:本文以法那科(FANUC)系统数控车床宏程序加工非圆曲线(椭圆)研究导向,通过案例分析,解决非圆曲线(椭圆)在实际教学中编程加工的难题及宏程序应用难点,有效将案例的技能点和知识点转化为课程教学资源,用于数控车工(高级工、技师、高级技师)的实习教学中,同时也可为社会化数控车工(高级工、技师)技能鉴定考核提供技术借鉴。
关键词:非圆曲线;椭圆;宏程序
一、数控车床宏程序加工非圆曲线(椭圆)概述
在数控加工专业实训教学和数控车工(高级工、技师、高级技师)技能鉴定考核中,非圆曲线的编程加工常被作为一个重点的考核内容,对操作者的理论知识,和操作技能有比较高的要求。非圆曲线加工的难点是程序编写及计算,重点是如何理解非圆曲线(椭圆)标准方程及参数方程的转换。非圆曲线(椭圆)程序编写有两种形式,其一是以标准方程公式(几何尺寸)式编程,其二是以参数(几何角度)形式编程,前者编程应用比较广泛容易理解,后面是在特定的場合应用,不容易理解其原理。
二、数控车床宏程序加工非圆曲线(椭圆)编程加工案例
本文案例,主要针对工非圆曲线(椭圆)宏程序编写,工艺步骤,非圆曲线(椭圆)标准方程及参数方程的转换等方面进行分析。
(一)分析零件图
本案例零件图中有两处是非圆曲线,为便于程序写,设有三个工件坐标原点,两个非圆曲线坐标原点。工件全部表面粗糙度值要求Ra3.2μm,φ30mm、φ40mm、φ58mm外圆公差等级为h8,长度L00±0.1mm,未注明倒角按C1。非圆曲线(椭圆2)原点与工件回转中心轴线距离(X方向)为21mm,与工件坐标原点2的距离(Z方向)为45 mm,非圆曲线(椭圆1)为(1/2)椭圆。
(二)加工工艺路线
为保证加工精度及工件尺寸的稳定性,在工件加工时,分粗加工和精加工步骤。根据工件形状,先加工右端φ30mm、φ40mm、φ58mm、非圆曲线(椭圆2)外圆及长度,并且选工件右端面做为测量基准和装夹基准。工件右端的测量基准和装夹基准加工完成后,调头装夹工件,加工φ30mm、非圆曲线(椭圆1)外圆,取合工件长度L00±0.1mm总长。
(三)程序编写
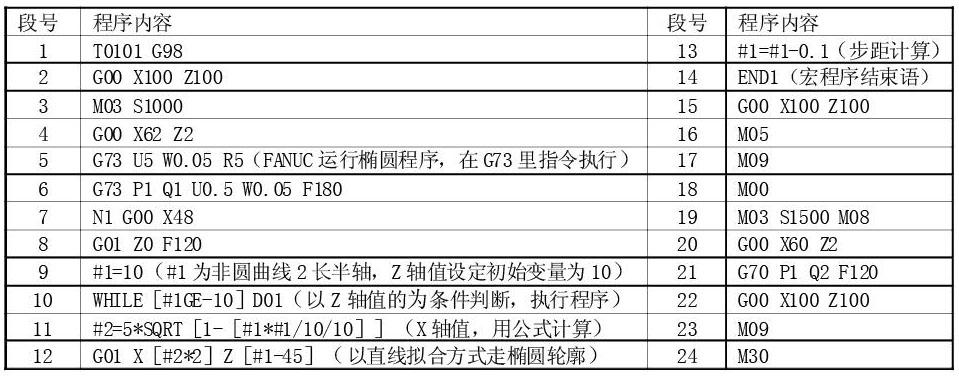
1.椭圆标准方程入值和转换程序编写
椭圆2标准方程为 ,不能直接写入程序运行,要进转换坐标才能在程序中运行。将短半轴(a)代入数值5,,长半轴(b)代入数值10,Y轴转换为Z轴,椭圆的标准方程代入值和转换后的方程式为, X2/52-Z2/102=1,非圆曲线(椭圆1)宏程序编写如下表:
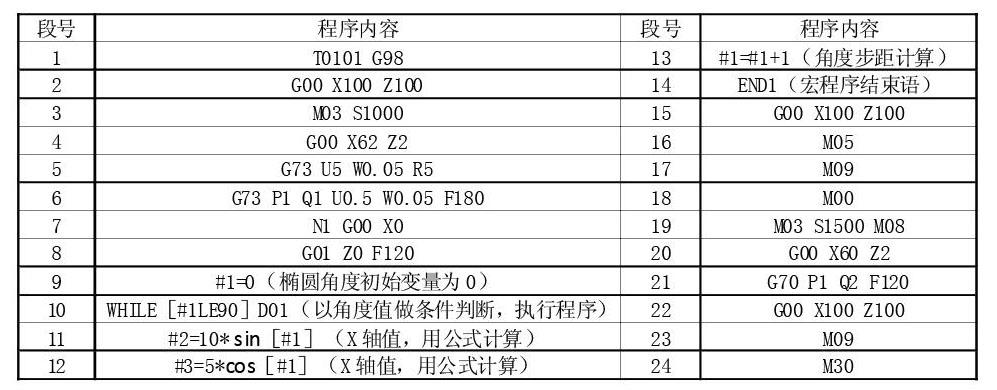
2.椭圆参数方程转换程序编写
椭圆1的参数方程为Y=a*cosθ,X=b*sinθ不能直接写入程序运行,和上述标准方程一样,需要进行坐标转换,Y=a* cosθ转换为Z=a*cosθ,“θ”取值为0o≤θ≤90o,椭圆1宏程序编写如下表:
3.程序编写注意事项
上述两种宏程序编程方法,都能完成非圆曲线(椭圆)的加工,以椭圆标准方程代入值和转换编写程序需注意要两处,其一是根据已知条件选择判断变量,初始变量赋值,运算步距依据表面粗糙度要求设定,其二是计算出非圆曲线原点坐标与工件原点坐标的距离,确定非圆曲线坐标原点的起始位置。以椭圆参数方程代入值和转换编写程序需注意的是,根据数控车床不超过坐标第二象限加工原理,“θ”取值最大的范围为0o≤θ≤180o,运算角度的初始赋值、终止变化量,要求依据实际加工要求设定。
三、总结
通过工非圆曲线(椭圆)编程加工案例分析及知识和技能点提炼,解决了非圆曲线(椭圆)编程加工难度的问题,上诉两种编程方式可以使得宏程序编写变得简化,有清晰的理论依据。在教学中使用学生能容易理解和掌握,拓展知识面增加学习兴趣。在社会化技能鉴定考核中使用,让考生更容易理解非圆曲线的加工原理,对宏程序的编写能力得到进一步提升。
参考文献:
[1] 陆华广.《数控车床切削加工》[M].现代教育出版社.2014.8
[2]黄松·《数控车床操作(高级工)》·(M)·现代教育出版社,2015.6
