数据生态系统—“数据海”

Zi-Kui Liu

Department of Materials Science and Engineering, Pennsylvania State University, University Park, PA 16802, USA

在最近的一篇文章[1]中，针对不断增长的计算能力和大量的在线数据存储库，笔者对“数据海”这一概念进行了深入探讨。这些新的发展需要一种全新的计算框架范式，用以连接各种数据存储库、整合机器学习、循环使用现有数据，以及为新的计算和实验工作提供参考，从而创建一种由数据和工具所组成的“可持续生态系统”（sustainable ecosystem）。笔者希望最近公开的一些开源代码能够促进各个数据存储库与“数据海”之间的低障碍交换路径的开发，同时，我们期待与“数据海”的数据交换能够提高每个独立的数据存储库中的数据的用途和价值，如图1 [1]所示。

热力学是一门研究系统与环境相互作用时的状态（包括稳定、亚稳定以及不稳定状态）的科学。Gibbs[2,3]提出的热力学第一定律和第二定律的结合，将系统的外部和内部紧密联系起来。尽管Gibbs关注的是非均相物质的平衡[2,4]，但是热力学第一定律和第二定律的结合亦将系统的平衡态和非平衡态包含在其中[5,6]。

基于相图计算（CALPHAD）方法[6–9]的热力学建模可以在系统外部和内部变量的整个空间中建立各个相的吉布斯能量，并且涵盖了每个相的稳定区、亚稳定区和不稳定区。事实上，对于纯元素的稳定结构与非稳定结构之间的能量差的定义是CALPHAD建模的基础，Kaufman将其称为“晶格稳定性”（lattice stability），Kaufman是开创CALPHAD方法的先驱，亦是该方法的命名者[10,11]。“晶格稳定性”概念的提出以及人们对一组“晶格稳定性”值的普遍接受使得多组分数据库得以发展并涵盖20多个元素，这些数据库已经成为集成计算材料工程（ICME）[12]和材料基因组计划（MGI）[13]的基础。

在2000年之前，CALPHAD建模几乎完全依赖于实验信息和一些相对简单的理论预测，其与基于密度泛函理论（DFT）的第一性原理得出的计算结果的集成相当有限[14]。计算方法和软件工具的不断发展，特别是维也纳ab-initio模拟软件包（VASP）[16–18]的出现，促进了CALPHAD建模中广泛应用DFT的第一性原理计算的结果，以及多学科信息技术研究（ITR）项目，即“多组分材料设计的计算工具”（Computational Tools for Multicomponent Materials Design）在2002年的启动，该项目得到了美国国家科学基金会（NSF）的支持。这项信息技术研究项目通过相场模拟及有限元法[19]将DFT和CALPHAD方法相结合，这一灵感来源于人类基因组计划[20]以及NSF支持的名为“计算热力学、计算动力学和材料设计的综合教育计划”（An Integrated Education Program on Computational Thermodynamics, Kinetics, and Materials Design）项目[21]，后者启发笔者在2002年创造了“材料基因”（materials genome）这一术语和概念[22,23]。

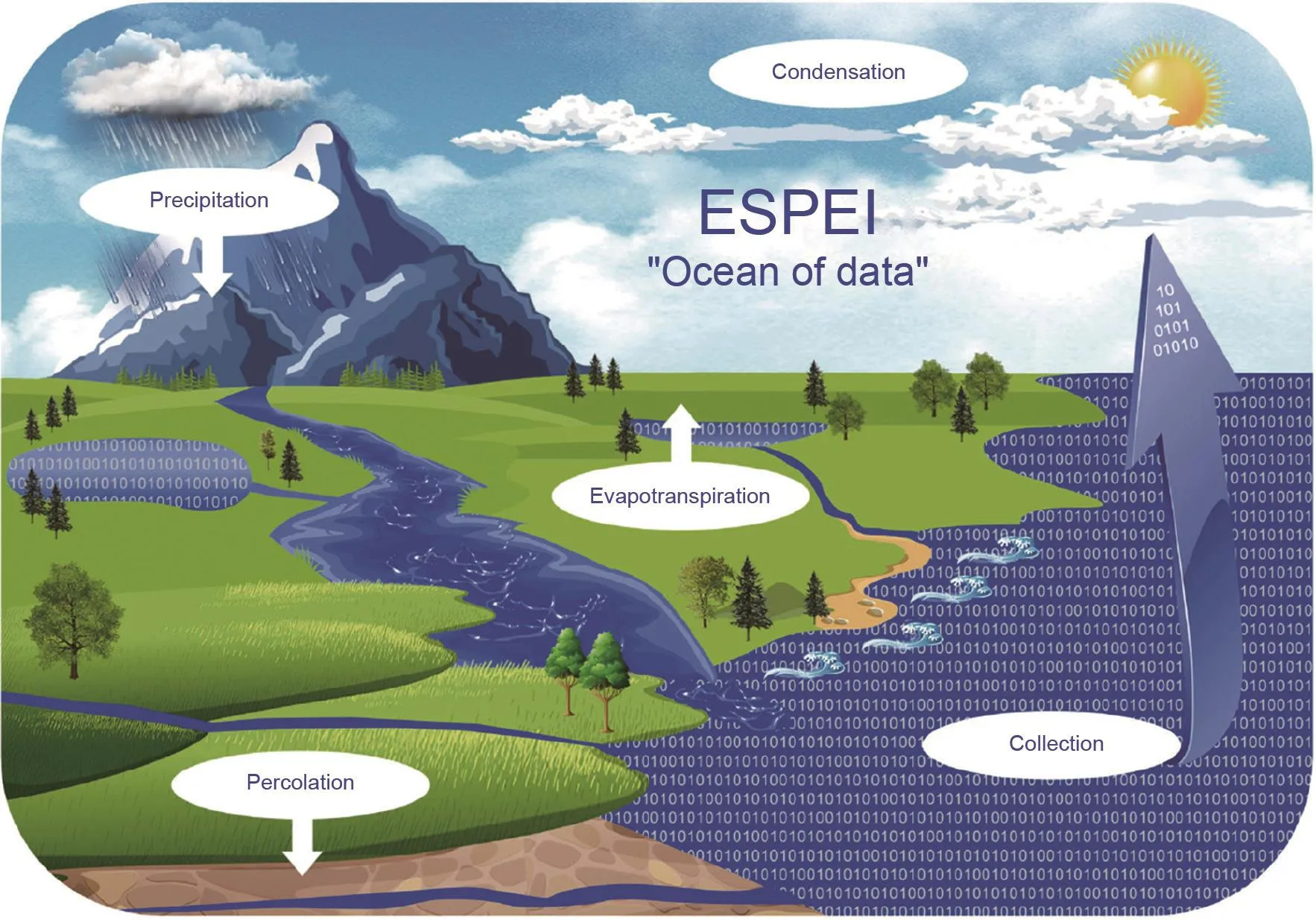
图1 .参考文献[1]所描绘的ESPEI数据的“可持续生态系统”示意图，图中显示了各种数据存储库（湖泊）、互联（河流）、私有数据（渗流）、数据处理（蒸发）、数据收集（海洋）、数据循环使用（冷凝与降水）。ESPEI：可扩展的、自我优化的相平衡基础设施。

2009年，笔者回顾了热力学的第一性原理计算和CALPHAD建模的新发展[24]。笔者的团队创立了可扩展的、自我优化的相平衡基础设施（ESPEI）概念[25–27]，该框架使用来自第一性原理计算的各个相的热化学数据进行CALPHAD建模，并使用实验相平衡数据完善模型参数。ESPEI概念的重要性体现在3个方面：①第一性原理计算提供的能量值是内部自由度的函数，即每个单独相的内部非平衡构型，该构型难以从实验中直接获得，因为实验数据往往来自多种构型的混合物[28–32]；② ESPEI建立了一种机制，该机制可以有效地评估模型参数、数据的不确定性以及计算性能中的不确定性传播[27,33]；③ ESPEI数据基础结构集成了基于CALPHAD建模中的原始数据和处理后的数据，从而可以有效地循环使用原始数据，并有效地更新和维护处理后的数据和数据库。在美国，随着越来越多的关于第一性原理计算的出版物面市，加之高性能计算工具逐渐普及以及诸如材料项目[34]、开放量子材料数据库[35]和材料发现自动流程[36]等大型在线数据库的发展，笔者相信基于DFT的第一性原理计算中的热化学数据，将在各种材料的CALPHAD建模中发挥越来越关键的作用，特别是在新材料的发现与设计中。

Olson系统地开发了基于CALPHAD数据库、热力学计算和动力学模拟的系统材料设计，以开发新材料并改进现有材料[37,38]。这种系统材料设计方法将加工过程中的可控参数与使用微观结构属性的可测量的数量属性联系起来。在众多微观结构属性中，最关键的基础变量是形成的相，这与CALPHAD方法中的单相建模概念完全一致。CALPHAD方法也已经运用了一系列其他属性。表1例举了本研究小组计算的一些性能[28–32,39–69]。此外还应特别注意的是，能量对其自然变量的二阶导数代表了许多物理量，如图2、图3 [6,13,70]所示，其中，一些正在开发的临时术语条目被划归至图2中最后一列和最后一行，包括图3中的压缩热。

材料设计是材料生命周期的第一步。设计完成后，材料被制造出来并投入使用，制造与使用过程会产生新的原始数据，从而丰富现有的原始数据和处理后的数据，或将二者进行对比。此外，材料回收对于环境和材料成本变得越来越重要。由于材料的回收通常会涉及多种材料的混合，因此与单独设计每一种材料所用的原始数据以及处理后的数据相比，回收材料的化学成分可能会更复杂。这些新的原始数据可能需要额外的第一性原理计算，已有的模型亦需要进一步修订和扩展[71]。如图4 [25–27,72–74]所示，这个连接对于可持续数据生态系统而言至关重要，但这并不是一件容易的事情，因为目前的热力学数据库可包含20多个元素，而这些非常多的外部和内部变量的多维空间中的原始数据是有限的[75–77]。我们希望在开发开元软件包方面所做出的努力，如DFTTK [78]、pycalphad [72,73]、ESPEI[25–27,74]和最近的SIPFENN深层神经网络机器学习†† Krajewski, A. M. & Liu, Z. K. SIPFENN: Structure-Informed Prediction of Formation Energy using Neural Networks. 2020. Available from: https://phaseslab.com/sipfenn.等能够激励业界进行新工具的开发，以进一步推动科学与计算驱动的材料研究范式的发展[79]。

表1 计算和建模属性的实例

图2. 与内部能量关于其自然变量的二阶导数相关的物理量[6,13]。

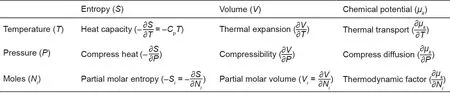
图3. 与吉布斯能量关于其自然变量的二阶导数相关的物理量[70]。

其他挑战主要在于材料在长度和时间尺度上的多层次复杂性，以及与信息如何在尺度之间传递以产生微观和宏观行为有关[19]。我们最近的研究证明，下列熵等式有希望通过熵实现材料性质和信息的多尺度集成[80]。

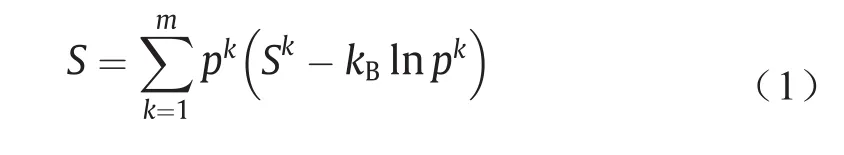
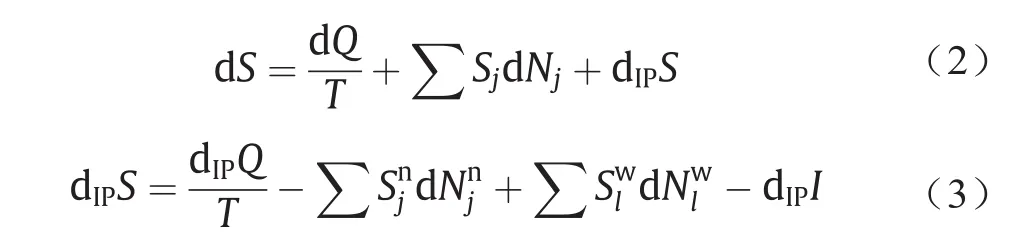
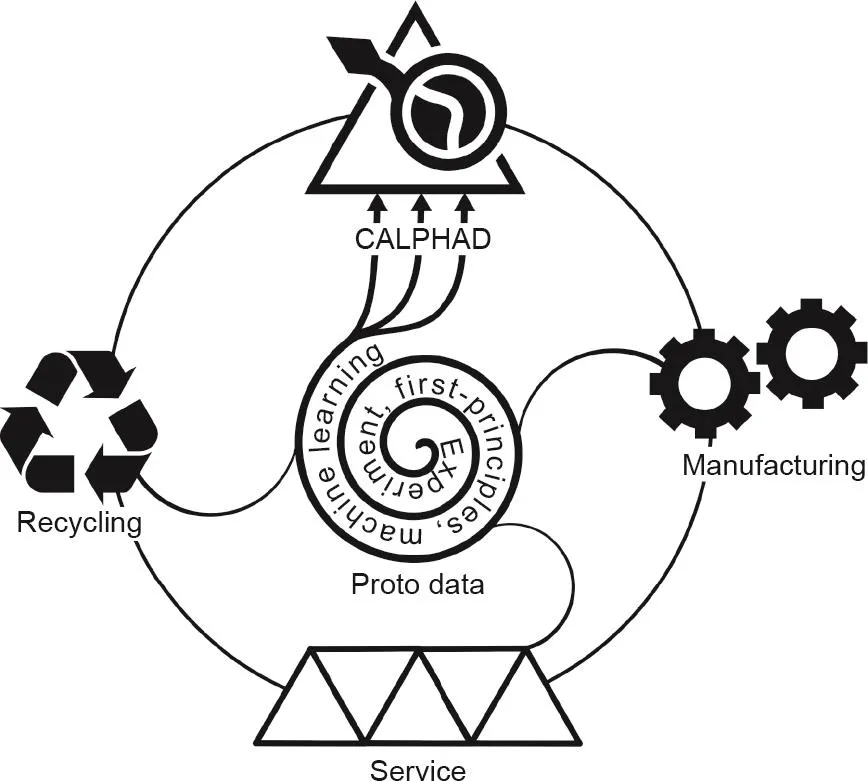
图4. 数据生态系统示意图，包括原始数据（实验、第一性原理计算和机器学习）、处理后的数据（建模——使用pycalphad [72,73]和ESPEI[25–27,74]的CALPHAD）、材料制造、材料服役和材料回收。

等式（1）表示系统的总熵S，可根据k尺度的系统构型计算得出。其中pk表示系统构型k∈{1, ...,m}的概率，且pk=1，Sk表示尺度k中每个构型的熵，而kB表示玻尔兹曼常量。需要注意的是，系统的熵包含了所考量尺度上的熵加上每个单独构型的熵，每个单独构型的概率与所有构型的自由能有关。每个单独的构型都由其另外的一组内部的构型组成，因此Sk可以用其自身的构型以与等式（1）相同的形式表达。这种拆分可以持续进行，直到所有的重要尺度都被纳入考量范围，并且这种多尺度的集成不止限于一个方向，可以是双向的[80]。材料科学与工程领域的研究重点是相的形成，原子构型代表了占主导地位的尺度，而电子和声子的密度则代表其子尺度[39]，同时外界宏观的制约可以改变材料内部相的形成和形貌。

在等式（2）中，dS表示系统的熵变化；dQ表示系统从周围环境接收（＞ 0）或释放（＜ 0）的热量；Sj表示组分j在环境或系统中的偏摩尔熵；dNj表示系统接收（dNj＞ 0）或释放（dNj＜ 0）到周围环境中的组分j的量；T表示温度；dIPS是由于独立的内部过程（IP）产生的熵。等式右边的第一项通常代表熵的概念如何被引入材料热力学，相对而言第二项则很少被讨论，其常被隐没在将化学势直接引入热力学第一定律和第二定律的过程中。第三项的细节，即熵的产生，通常被认为是动力学或者不可逆热力学的部分。由于我们的研究往往只考虑平衡态，因此第三项的内容在热力学中通常没有涉及。值得注意的是，热力学第一定律和第二定律中的熵包含了等式（2）中的三个项，尽管通常对此不作特别说明[80]。

等式（3）表明，通过将内部过程定义为IP系统，由内部过程产生的熵也可以用类似于等式（2）的形式表示[80]。该IP系统可能会消耗一些偏熵为Sjn的养分（dNjn）以及产生部分偏熵为Slw的废物（dNlw）和热量（dIPQ），并重组其构型以产生一定的信息量（dIPI）。然后通过等式（1）可得到如下等式：

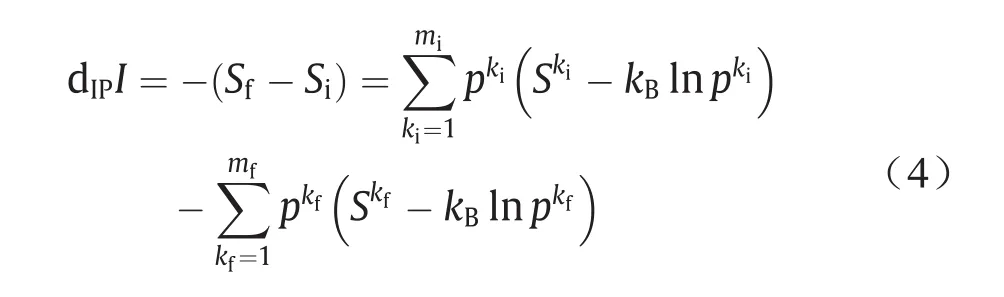
式中，下标f和i代表IP系统最终和初始的构型。对于自发或不可逆的内部过程，根据热力学第二定律，由式（3）表示的熵产生必须为正。然而，dIPI的符号可以是正（信息生成过程），亦可以是负（信息擦除过程）。参考文献[80]对各种设想的实验展开探讨。应该注意的是，等式（2）与等式（3）中的符号约定是相反的，等式（2）中的正号表示系统从环境中接收热量与质量，而等式（3）中的正号则表示IP系统随着熵的增加而释放热量与质量。

事实证明，基于单个相的属性的CALPHAD建模是计算材料科学和工程的基础。为了进一步提高基于CALPHAD方法的预测能力，笔者建议在相应尺度上将构型纳入考量范畴，如等式（1）所示，所以在预测过程中，不同尺度的属性可作为外部条件的一个函数，这样单个构型之间的竞争就有可能导致系统产生单个构型所不具备的突现行为。当温度对熵的导数从稳定的正值逐渐接近零时，系统稳定性极限的极端突现行为可被观察到[6]。由于温度和熵是热力学组合定律中的共轭变量，即熵变发散，所以熵对温度的导数变为正无穷大，这是由等式（1）所示的稳定和亚稳定构型之间的竞争所引起的。应该指出的是，当系统的熵发散的时候，单个构型的熵并不发散，这适合于系统所有的摩尔量。也就是说，系统的每一个摩尔量都会在稳定性达到极限时发散，而单个构型的摩尔量并不发散。此外，当用体积对温度的导数表示热膨胀时，系统的熵可能呈现负发散状态，因为体积和温度不是热力学组合定律中的共轭变量[6]。就热膨胀而言，我们已经证明了铈的发散为正，而Fe3Pt的发散为负[28–30]。同时，由于麦克斯韦关系[6]，体积对温度的导数等于熵对压力（我们称之为“压缩热”）的导数的负值，因此，图2与图3中的量是对称的。