基于动态阈值分段的激光扫描数据过滤算法
2020-09-03余松森曹一波刘好新
李 扬,苏 海,余松森,曹一波,刘好新
(1.华南师范大学计算机学院,广东 广州 510631;2.华南师范大学软件学院,广东 佛山 528225;3.海南大学信息与通信工程学院,海南 海口 570228)
1 引 言
激光头发出的红外激光打到物体表面时发生漫反射,旋转激光扫描仪接收漫反射回的激光信号,利用激光测距算法,如三角测距法[1],实现距离测量,具有成本低、计算快以及精度高的特点。而这正好满足移动机器人对环境感知类传感器实时性和高精度的要求,因此被广泛应用于移动机器人测距领域,用于获取环境障碍物的分布[2]。
但是基于漫反射原理的测距仪,常受环境影响而产生误差。尤其是产生的粗大误差严重偏离了被测量物体的真值,在后续的机器人任务中影响最大,必须被过滤[3-4]。粗大误差产生的原因有很多,分为主观原因与客观原因两类[5]。文献[6]-[8]详细分析了激光测距的误差来源,其中环境温度、物体材质、颜色和倾斜度等外界环境都会影响漫反射回的信号,进而影响测距精度。此外,粗大误差相对于系统误差和偶然误差,拥有更鲜明的特征,较容易在数据预处理阶段实现直接过滤。因此,进行粗大误差过滤是很有收益且必不可少的过程。
目前国内外针对粗大误差过滤的算法已有较深入的研究。总体分为两大类,一类是邻域比较法,如中值滤波[9]、弦夹角、弦高比[10]等通过和邻域的数据进行比较来进行误差判断,算法简单易实现,但是比较时使用的阈值难以定义,因此无法应对多变的环境,鲁棒性不强。文献[11]中提到了一种移动最小二乘中位数法,通过预先估计出测量数据集的标准差,然后以标准差作为判断依据,它能在一定程度上减轻过滤效果对阈值的依赖,但存在计算量大的问题。另外一类是分段法,将数据分段后过滤成员数少的段。文献[12]采用基于改进的连续边缘提取方法(Improved Successive Edge Following,ISEF)进行快速分段及滤波。文献[13]将扫描点进行区域转换后,计算相邻点间的距离,通过分析得出了不同测量距离下的阈值,从而分段过滤。然而这些算法除了本身的缺陷外均存在不适合应用于移动机器人领域的问题。装载到移动机器人上的旋转激光扫描仪,其测量数据具有缺失性(某些角度有数据缺失)、不确定性(测量长度随着环境不断变化)、数据量大(旋转激光测距仪随机器移动的同时以一定的角速度不断旋转采集数据)、粗大误差量少等特点。并且机器人在移动测量的同时进行环境地图构建,这要求数据过滤需要具备一定的实时性[14-16]。因此,本文研究了一种旋转激光扫描数据的实时过滤方法,解决如何在上述特性下实现粗大误差的实时过滤。
本文采用动态阈值分段,根据上一个相邻的有效采样点设定动态阈值,对当前采样数据进行同段判断,将数据分段后,过滤掉包含成员少的分段。文中给出了动态阈值的设定方法及原理推导,并建立了多组环境进行算法测试,同时为了量化分析算法的效果,通过构建实验环境的等比例平面图对测试数据进行了人工标注,且对特殊环境做了具体分析,最后的实验结果表明了算法的可行性。
2 移动旋转激光扫描仪数据分析
在对移动旋转激光扫描数据进行过滤之前,分析其数据来源及数据特点。
2.1 旋转激光扫描仪工作原理
三角测距法是常用的激光测距方法。通常旋转激光扫描仪使用三角测距法得到环境距离数据,而后经由机器人平台传输给上位机或后台等待处理。如图1所示为三角测距原理,激光头与摄像头处在同一基准线上,两者间距离为s,摄像头焦距为f,激光头与基准线呈固定夹角β。激光头发射的激光打在物体表面,经由漫反射被摄像头捕捉到,经过小孔成像,显示到成像面上。
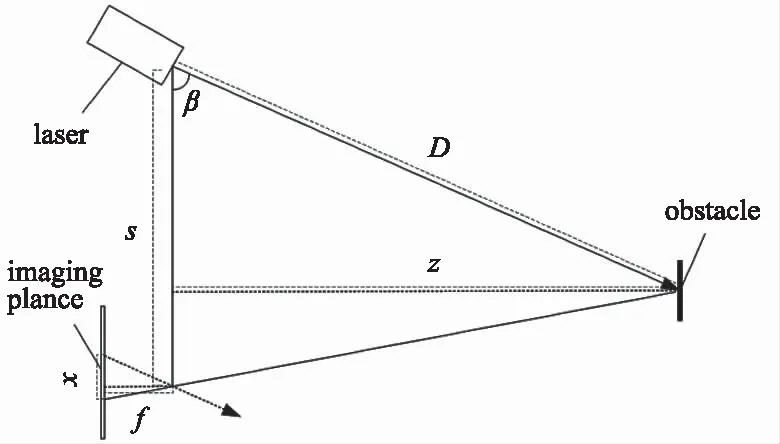
图1 三角测距原理
根据三角形相似和余弦定理可得:
(1)
以常见的传感器设备为例,参数为f=16 mm,s=41 mm,β=82.145°,每个像元的大小为5.5 μm,则其像元偏移X与测距长度D的对应关系如图2所示。

图2 X-D曲线
由于像元偏移X是离散值所以测距长度D也是离散的。这意味着对于300 cm处的障碍物,激光测距所得到的测距距离只能是301 cm或者漫反射的激光点投影错误时可能会得到293.7 cm的次等结果,此时的误差大概为2.1 %。由图2易知误差值随着测距距离的增大而增大,当测距距离为最大有效值Dmax时,误差最大。另一方面,随着X增大,距离D的变化逐渐放缓,且由于成像面有限,所以实际的X并不会无限增大,致使最终D会趋近于一个极小值Dmin。因此,系统会结合传感器的参数,在误差可接受范围内,定义一个有效测距范围[Dmin,Dmax],只处理有效范围内的数据。
2.2 旋转激光扫描仪数据分析
上位机接收到的数据经过奇偶校验以及范围筛选后才进行误差过滤,可以定义这样的数据为待过滤数据。如图3所示为在某室内环境下旋转激光测距仪旋转一圈所得到的待过滤数据,横轴为采样时间,纵轴为测距距离,测距仪每旋转一度进行一次采样,为方便显示,将缺失的数据用零填充。

图3 待过滤数据
结合图3以及移动机器人的工作特性可知,待过滤数据具有如下特点:
(1)缺失性。部分角度对应的测距数据有缺失,主要的原因可能是对应角度在有效范围内并没有障碍物存在,或者该角度所在的数据帧,因为传输错误而丢失。
(2)不确定性。角度所对应的长度变化完全由所处的环境决定,测距长度的走势具有不确定性。
(3)分段性。数据的不确定性和缺失性使得连续的角度所对应的测量数据被分割成了多个段,但是正确的数据在独立成段时往往会拥有足够多的段成员。
(4)数据量大。在机器人移动过程中,旋转激光测距仪一直在进行测距,新的数据一直在不断的传回给上位机等待处理,因此所提的算法应该具备实时性以及计算量小的特点。
(5)粗大误差量少。旋转一圈所采样数据中包含的粗大误差并不多,且不会多个连续出现。
3 基于动态阈值分段的实时过滤算法
搭载在移动机器人上的旋转激光扫描仪所产生的扫描数据具备其独有的特性,加上对实时性和计算量的要求,导致现有的一些过滤算法都不太适用。本文针对粗大误差与相邻数据差异较大,且数量较少的特点,通过设定动态阈值实现数据分段,最后定义成员数较少的段为粗大误差,进行过滤。算法总流程如图4所示。

图4 算法总流程
3.1 动态阈值分段
分段的依据是判断新的采样数据是否存在突变,即采样值是否大于动态阈值,若是,则需要分段,否则,定义为同段数据。现实环境中,对相对较平缓的物体表面进行采样所构成的点集通常会组成同段数据。另一方面,基于漫反射原理的测距传感器,在入射角θ较大时,传感器所能接收到的漫反射信号较弱,会影响到像元偏移量的计算。由前述可知,在测距很远时,较小的像元偏移计算错误也会导致较大的测量误差[17]。因此,本文通过分析平缓物体表面采样数据的分布推导动态阈值的设定方法,同时考虑入射角作为约束条件,构建了如图所示的约束模型,定义扫描仪逆时针旋转,lt-k为采样时刻t-k所对应的测距长度,α为入射角的余角。k既是角度也代表采样间隔(每隔一度进行一次采样)。
如图5所示,相邻的采样点间存在数据约束。对于lt时刻的数据,记其最近的上一个有效数据为lt-k,则lt相对于lt-k可能是递增的或是递减的。在限定了入射角的前提下,我们可以根据t-k时刻的数据lt-k计算在分别进行最大递增和最大递减变化的k个时刻后的数据值,作为t时刻数据lt的合理取值范围。
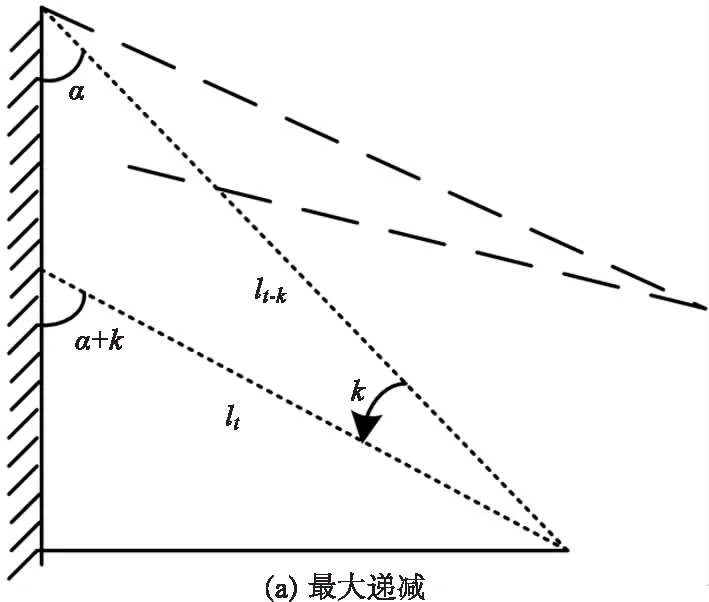
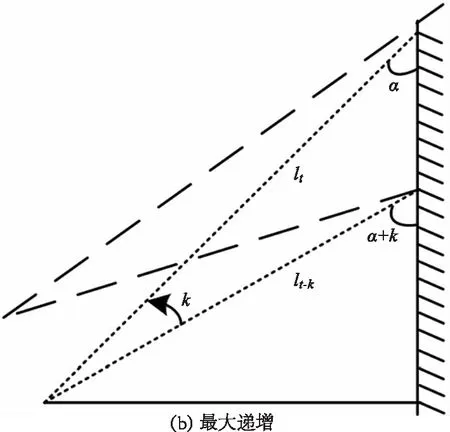
图5 约束模型
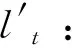
(2)
则合理的lt应满足:
(3)
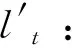
(4)
lt应满足:
(5)
综上,得到lt的合理取值范围:
(k (6) 式中,lt-k为最近的一个先前时刻的有效数据,即Dmin≤lt-k≤Dmax;α和N为预设参数,当且仅当lt满足上式且k 每当建立新段时,检查旧段的成员数,若小于N,则将旧段中数据均标记为粗大误差,进行过滤。在分段过程中,当检测到当前段成员数大于等于N时,段内的数据均能直接标记为正确数据,因此本文所提算法能在N个采样时间间隔内实现数据过滤。 如图6所示为实验所用的旋转激光扫描仪,以及装载有旋转激光扫描仪的机器人平台。旋转激光扫描仪使用三角测距法得到环境距离信息,后经由机器人通过ZigBee通信传输给上位机。 图6 旋转激光扫描仪与机器人 所用旋转激光扫描仪的参数为:f=16 mm,s=41 mm,β=82.145°,每个像元的大小为5.5 μm。由此,定义15~300 cm为激光扫描仪的有效测距范围,即Dmin=15 cm,Dmax=300 cm。 经过测试,发现所使用的移动机器人主要是在受环境影响时会产生粗大误差,尤其是在如图7所示的两种环境下。 图7 粗大误差环境 如图7(a)所示,激光头正对着的方向,若存在黑色且表面光滑的障碍物,则易产生粗大误差。其次,如图7(b)所示,对于由两个光滑平面所组成的夹角,被激光头直射到时,也容易产生粗大误差。基于此,我们构造了四组不同的能产生粗大误差的测试环境,并采集该环境下的测量数据进行实验,以验证算法的可行性。如图8所示,为构建环境所用到的障碍物,包括:两个边长为6 cm的六面体,一个边长为4.5 cm的八面体,一个直径为11.5 cm的圆柱及多个长为15 cm、宽为4 cm的长方体。图中瓷砖大小为50 cm×50 cm。 图8 障碍物集合 结合粗大误差产生条件,我们布置了如图9(a)所示的实测环境。除了用到了部分障碍物,实际环境中也包含了门及黑色墙砖。如图9(b)所示为由旋转激光扫描仪在该环境下所得到的激光点图。由激光点图可知,在某些夹角处产生了粗大误差。 图9 采样环境 测量现实环境能得到环境的测量集(一圈的有效扫描数据),为了方便分析所提算法的优缺点,我们对测量集的数据进行人工标注,标注每一个数据点的好坏。本文使用Auto CAD(Autodesk Computer Aided Design)按1∶10的比例重建了环境图,如图10所示为环境1的等比例平面图,并模拟激光束发射,每隔一度数据进行一次采样,得到每个角度对应的测距长度,构成环境的标准集。 图10 环境1等比例平面图 根据标准集标注测量集的方法为:对于测量集中每一个点数据,找到其在标准集中的值,若两者差值的绝对值小于阈值,则定义为好点,否则为坏点。本文取对应标准采样点的20 %作为阈值。如图11所示,为标准集和测量集的混合图,横轴代表采样时间,纵轴代表测距长度,为了显示方便,对于某些角度是无效数据的情况做了数据填充,无效点的纵坐标值填充为零,图中方点为测量集,圆点代表标准集。 图11 标准集与测量集 使用所提算法对测量集进行过滤,图11中“*”点即为算法认为需要被过滤的点。因为所提过滤算法将包含成员数较少的段定义为粗大误差,进行滤掉,因此会出现误过滤的情况。 根据多次实验测试,本文将使用参数α=20,N=4,如下表所示为过滤结果,错误数据标记为0,正确数据标记为1。以标准集对测量集的标记为准对比所提过滤算法对测量集的标记,可以得到过滤算法的过滤率等评价指标。对于环境1,正确率为98.12 %,有1.94 %的数据被误过滤,不过算法的未过滤率为0 %,这说明算法能准确的识别粗大误差数据并实现过滤,具体过滤结果如表1所示。 表1 过滤结果 同一个环境下,机器人运动时的测量数据与静止时的测量数据有很大差别,但是很难为移动中得到的测量集制定标准集,即难以人工标注,因此本文借助了相对运动的概念,使机器人静止,但布置了多种障碍物环境,在能产生粗大误差的同时让环境尽量复杂,如此既能得到和机器人移动时相近的测量集,也能进行人工标注。本文设置了多组实验,如图12所示为另外三组实验的环境图和激光点图。 (a)环境2 (b)环境3 (c)环境4 以上所述的四种环境的算法过滤效果汇总如表2所示。结合环境图和过滤结果可知,所提算法在不同的环境下均能实现粗大误差数据的过滤(未过滤率均为0 %)。在较为复杂的环境4中,误过率的数据最多,达到了5.05 %,这主要是因为,环境4中存在较多离散的障碍物。这些障碍物在离激光源较远的时候,其数据点集所对应的段成员数会很少,因此被误过滤。但因为数据量大,所以误过滤部分数据是可以接受的,又因为测距是在移动中进行的,所以不会出现某一障碍物所对应的测量数据一直被误过滤的情况。 粗大误差与相邻数据存在较大的距离差,为何不能用直接比较的方法进行过滤?是因为直接比较能过滤粗大误差,但只能做到部分过滤,无法应对某些特殊情况。如图13所示,a、b均为粗大误差,但是由于a点与b点的距离差较小,不满足粗大误差的判定条件,a点会被漏判为好点,同理b点也会被漏判。而且,距离差的阈值不好界定。因此,直接比较的方法在多样的环境下会存在漏判,不具备鲁棒性。 表2 过滤结果统计 图13 特殊粗大误差 那么基于分段法,应用弦夹角或弦高比进行分段的算法是否可行?仍存在阈值无法确定和特殊环境漏判的问题,如弦夹角法通过比较当前点的弦夹角和预设阈值来进行突变点判断,那么在a点所示环境下,其弦夹角较大,从而产生了漏判。但是本文算法能将a、b分为同一段,进而过滤。因此,本文算法具备一定的鲁棒性,且给出了动态阈值的设定方法。 理论上,本文算法对于离散环境会出现所有数据均被误过滤的情况。取N=4,当段成员数小于N时进行过滤,我们分析该条件下环境的离散程度。如图13所示为激光视野的极限模型,表示被测物体表面至少有多长才能被四个连续的激光点击中。设图4中圆的半径为r,相邻线段间的夹角为1°。如图14(a)所示,取r=300 cm,可得四条有效范围内最长的激光光束所击中的物体,其最小长度约为15.7 cm。这意味着在机器视野最远处的物体,若长度在15.7 cm以下,则会被误过滤,该物体对激光传感器不可见。如图14(b)所示,取r=30 cm,可得四条有效范围内最短的激光光束所击中的物体,其最小长度约为1.6 cm,即在机器视野最近处的物体,只要长度大于1.6 cm,激光传感器均能检测到。 本文认为,由于环境过于离散导致好点被误过滤的情况不需要视为特殊情况区别对待。因为机器一直在移动,在极限远时被误过滤的数据,会在机器人靠近物体的时候再次被检测到。如环境3和环境4中的两个圆柱体,环境3中的圆柱体离机器较近,测量数据被保留下来,而环境4中的因为过远,生成的段成员数较少而被过滤。 图14 激光视野极限模型 另一种离散环境,如图13所示,由于粗大误差的出现,将连续的序列分割成了两个子序列,由于某段子序列过小而产生了误过滤。对于该种情况可以通过合并两个子序列,进而再进行段判断,决定是否过滤。当然也可以不处理该种情况,如前所述,当机器人移动到近处时,自然会再次检测到误过滤的物体。因此,误过滤部分数据是可以接受的。 本文通过分析移动旋转测距数据的特点,提出了一种基于动态阈值分段的移动旋转激光扫描数据实时过滤算法,可应用于移动机器人领域,对机器移动中采集的旋转激光扫描数据进行实时过滤。算法通过前序有效采样值为当前采样点设定动态阈值,将满足阈值的采样点合并为同一个分段,再将段成员数量较少的段作为粗大误差进行过滤,通过考虑入射角作为约束条件,分析平缓物体表面采样数据的分布,推导出了动态阈值的设定方法,从而实现了使用动态阈值进行数据分段。算法兼顾了移动机器人对过滤的实时性需求,最后的实验分析表明,该算法具备一定的鲁棒性,能准确过滤粗大误差,虽然存在误过滤,但在可接受范围内。3.2 段判断
4 实 验
4.1 实验环境




4.2 实验分析
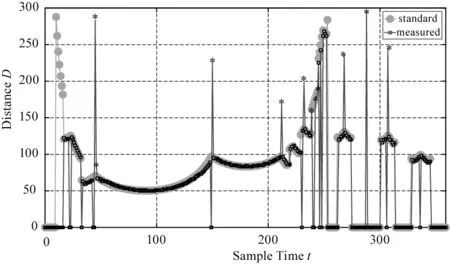

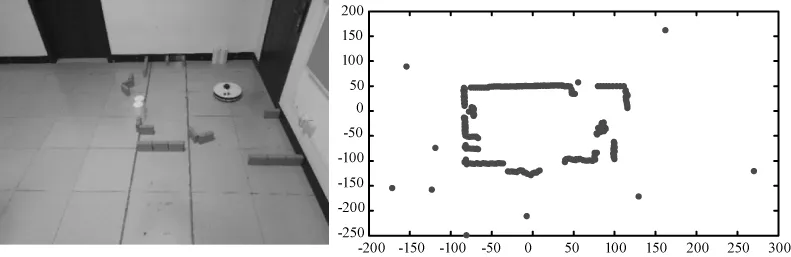


4.3 特殊环境分析



5 总 结
