一种曲轴磨削砂轮架的结构动力学分析与优化

曹火光,胡慧远,袁帅东,周怡君

(1.固耐重工(苏州)有限公司，江苏 苏州 215400)

(2.东南大学机械工程学院，江苏 南京 211189)

砂轮架作为曲轴随动磨床的核心功能部件，集砂轮旋转驱动、砂轮平衡调节、随动磨削进给、整机Z向运动等功能于一体，是机床技术水平的集中体现。砂轮旋转振动和复杂多变的磨削力，是引起砂轮架振动和产生噪声的根本原因，不仅严重影响机床的动态性能，而且降低了机床的加工精度。为获得较高的磨削加工精度，保证砂轮架的稳定性，需要深入研究砂轮架的动态特性。

在研究结构的动态性能时，集中参数模型法和参数灵敏度分析法是两种常见的分析方法。Guo等[1]在行星齿轮系统的研究中，利用系统集中参数模型，分析了固有频率对各参数的灵敏度，并优化了结构参数。Cha等[2-3]采用集中参数法，对多种磨床的动态性能和稳定性进行了研究。许丽娇[4]在刀架系统动力学特性研究中，通过刀架的集中参数模型对系统动态特性进行了深入分析。

结合他人研究结构动态性能的思路，本文采用集中参数法建立砂轮架动力学模型，然后使用参数灵敏度分析法研究砂轮架的动态特性并提出结构优化方案。

1 砂轮架动力学模型

如图1所示，曲轴随动磨床砂轮架主要由砂轮主轴模块、直线电机随动进给模块和Z向运动模块组成。

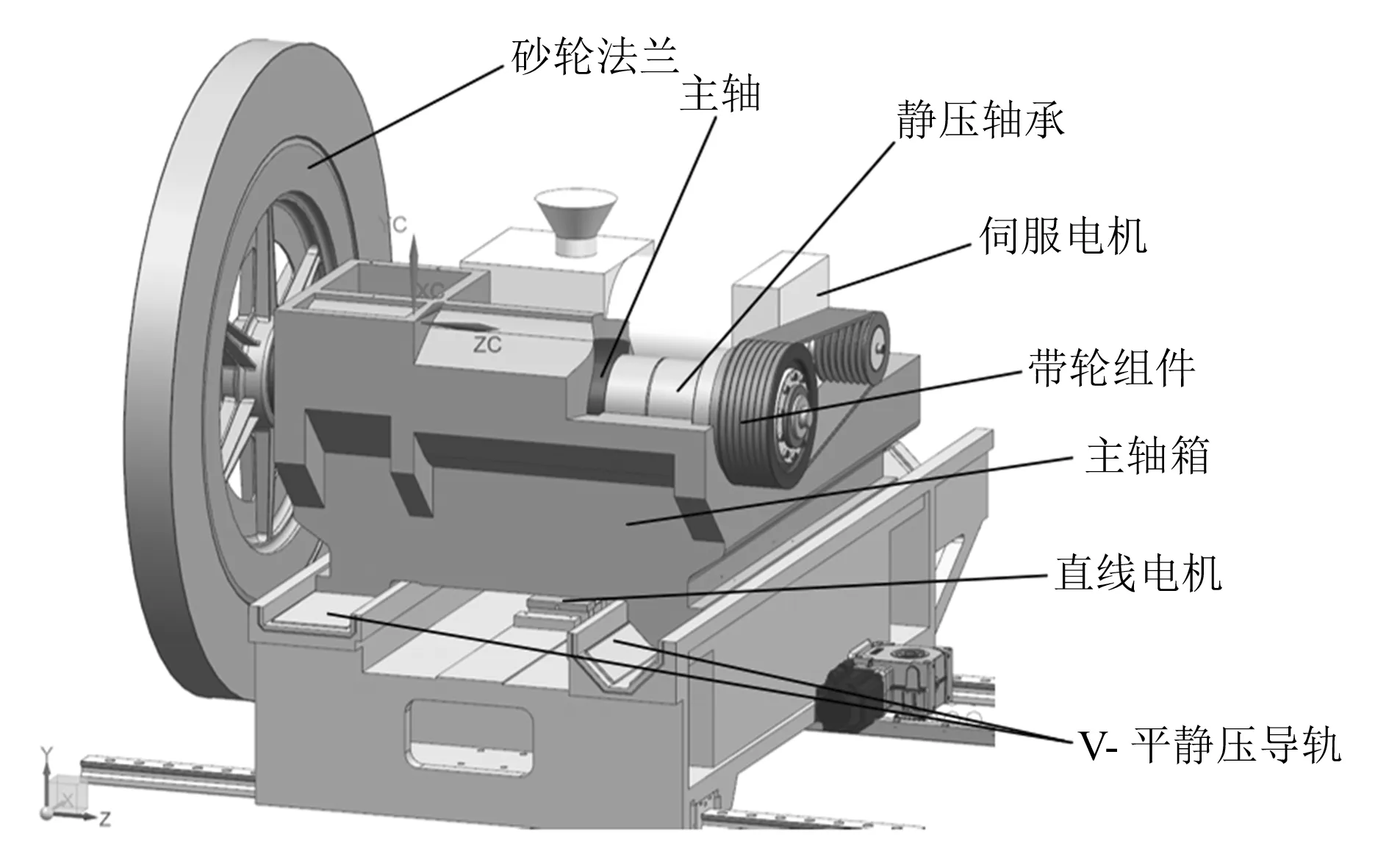
图1 砂轮架三维模型

本文建立的曲轴随动磨床砂轮架X向和Y向的非线性动力学集中参数模型，如图2、图3所示。模型中各参数含义如下：mb为带轮组件质量，ms为砂轮法兰质量，m1为主轴质量，m2为主轴箱质量，m3为拖板质量；J1x,J1y为主轴沿轴线方向的转动惯量，J2为主轴箱沿轴线方向的转动惯量；轴承和支撑采用等效的刚度元件和阻尼元件来描述，分别为kn和Cn(n=1,2 ,…,8)。

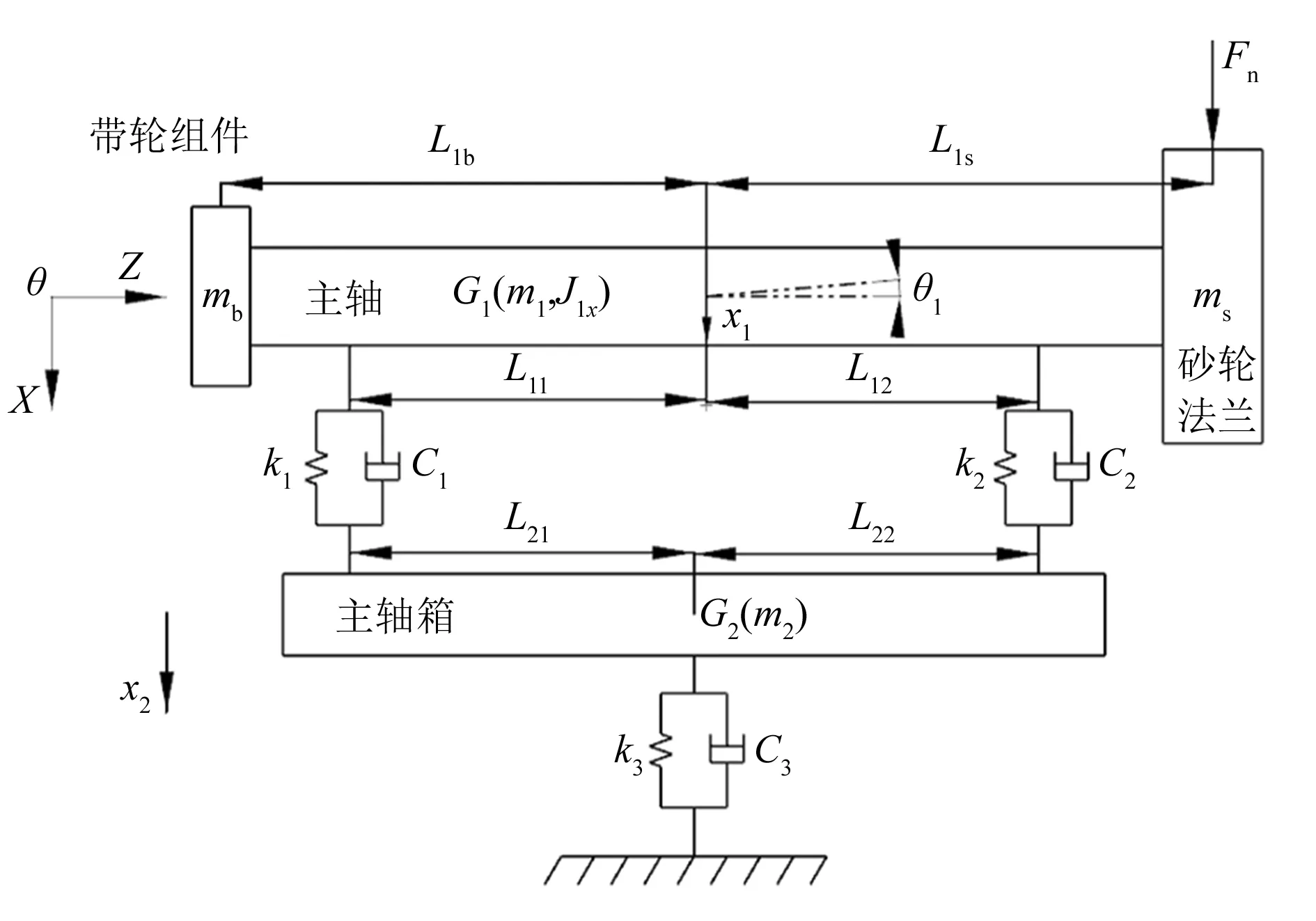
图2 砂轮架X向动力学模型

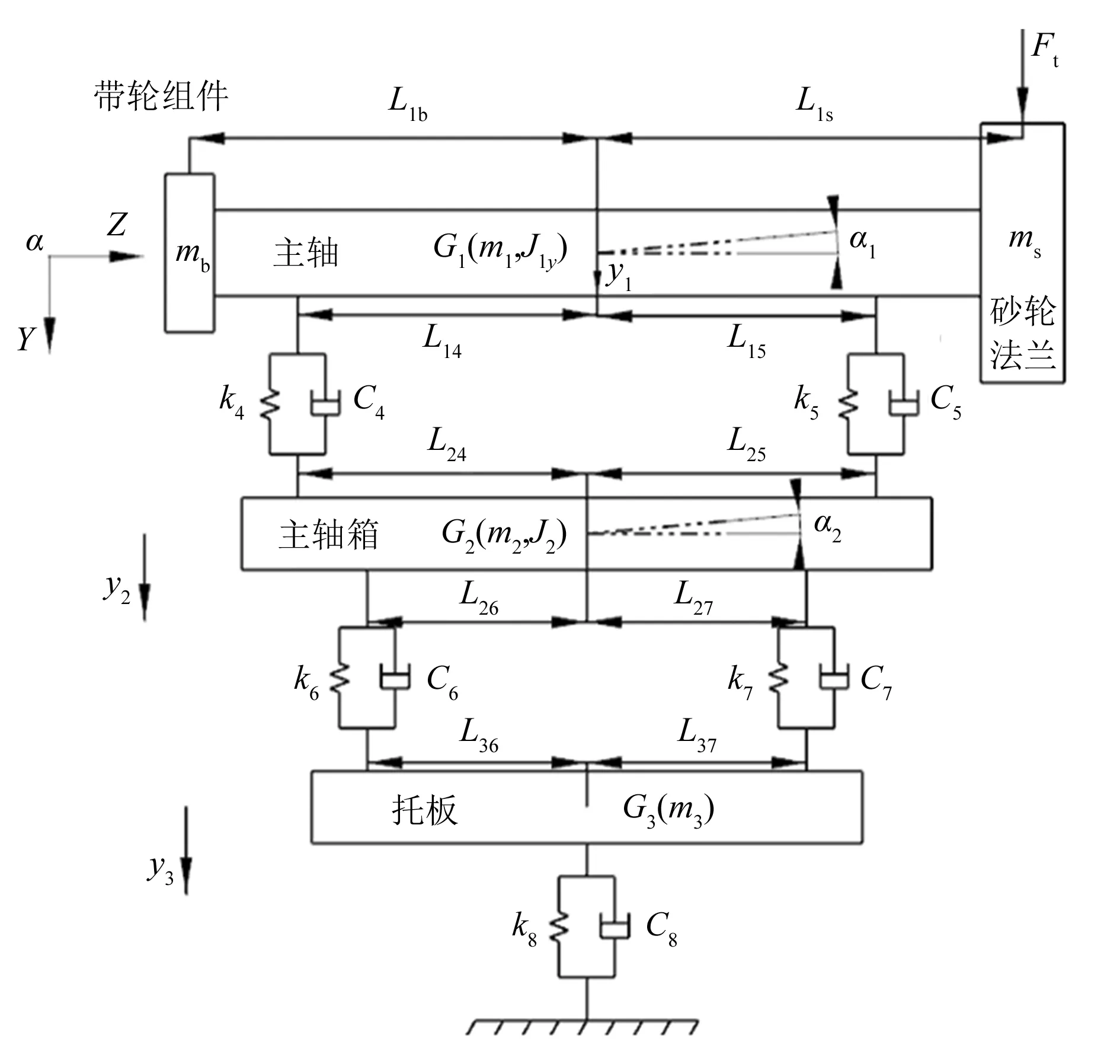
图3 砂轮架Y向动力学模型

对于一个n自由度的粘性阻尼系统，其拉格朗日方程表示为：

i=1,2,…,n

(1)

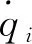
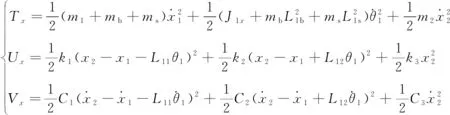
(2)

(3)

式中：Tx和Ty为系统X向和Y向动能；Ux和Uy为系统X向和Y向势能；Vx和Vy为系统X向和Y向阻尼耗能。由能量方程推导出砂轮架动力学控制微分方程，简化后为：

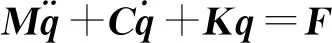
(4)

式中：M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；F为系统载荷向量；q为系统位移向量，q=[x1x2θ1y1y2y3α1α2]T。

2 固有特性分析

分析系统固有特性时，通常不考虑外界载荷、阻尼、接触间隙、加工误差等非线性因素影响。根据式(4)得出砂轮架系统无阻尼自由振动方程以及相应标准特征根方程为：

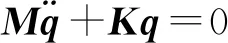
(5)

Kφ-ω2Mφ=0

(6)

式中：ω为系统固有频率；φ为系统模态向量，φ=[x1x2θ1y1y2y3α1α2]T。

将表1中砂轮架动力学主要参数代入式(6)，计算砂轮架系统的固有频率和模态振型，如图4所示。图4中横坐标为振动方向，纵坐标为去除单位归一化后的振动量。

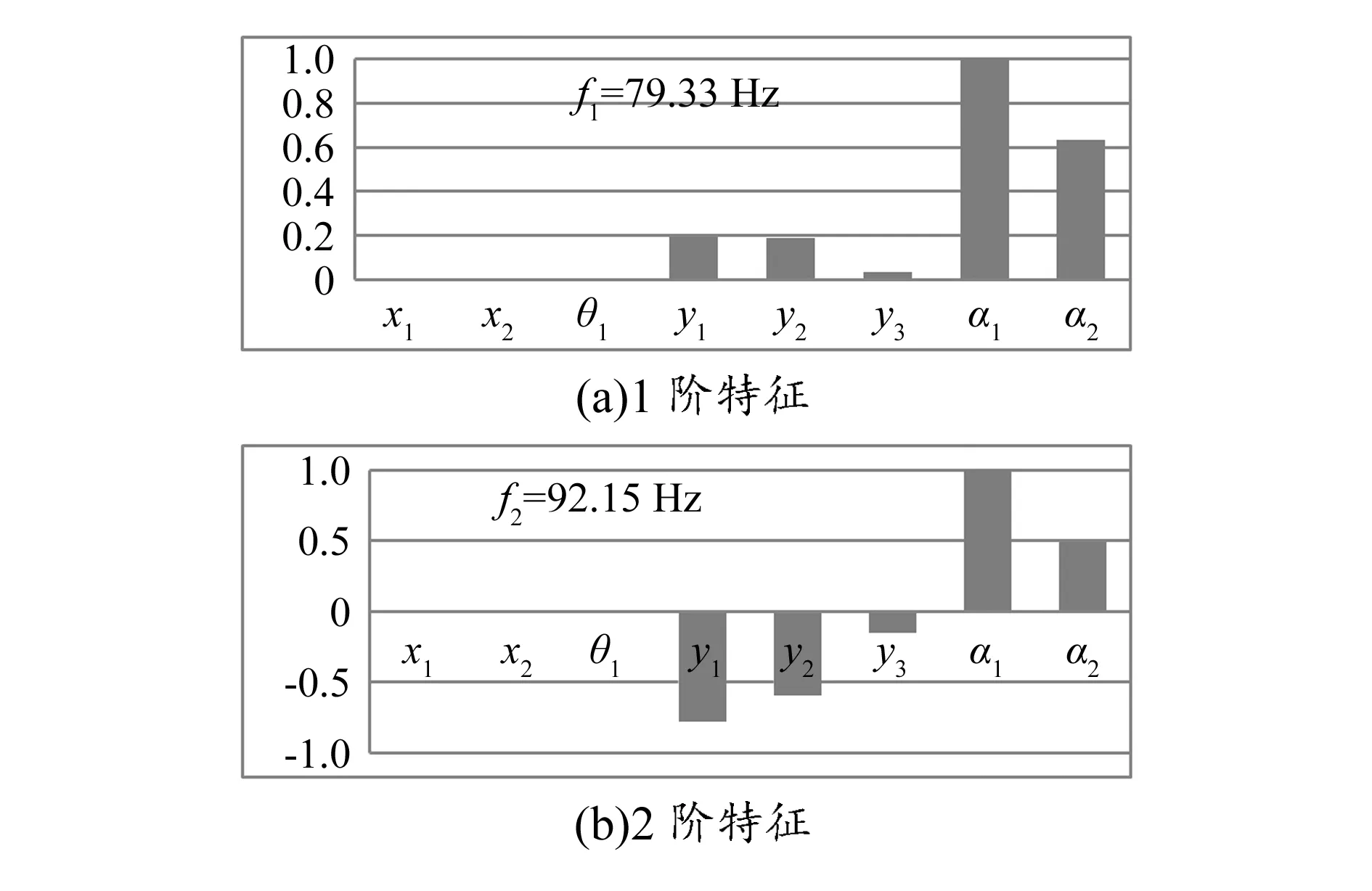
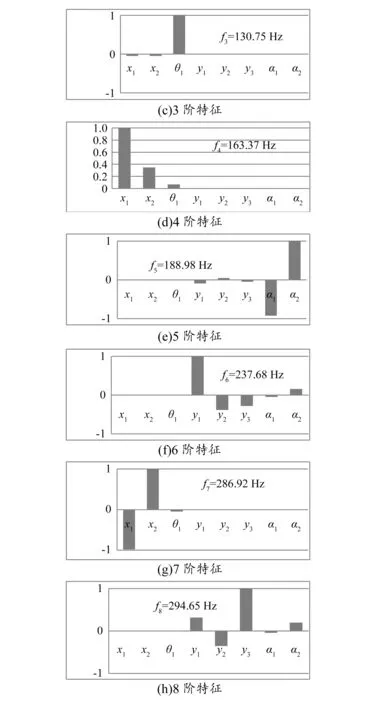
图4 系统固有特性

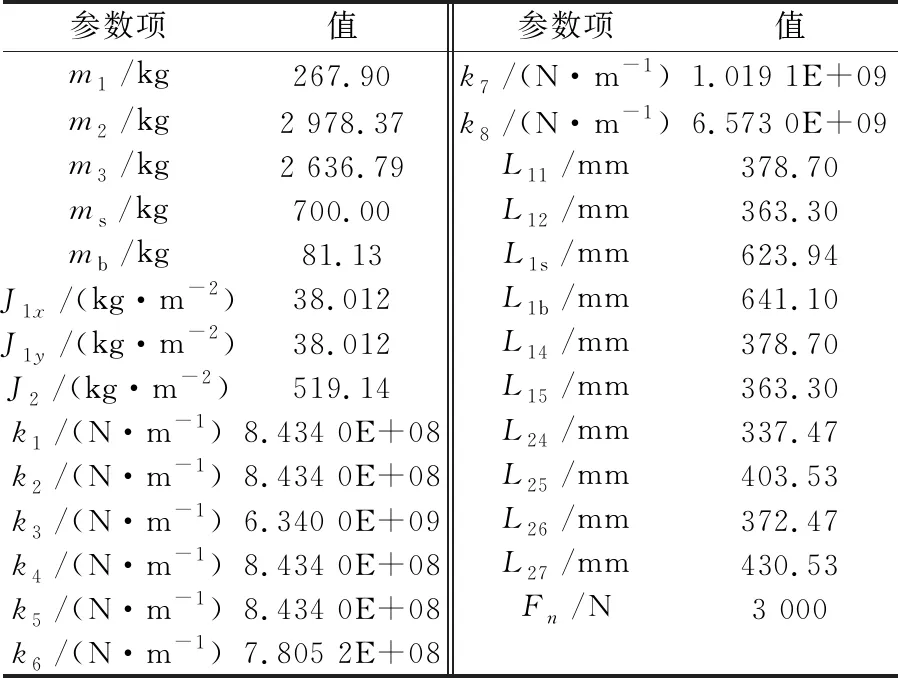
表1 砂轮架系统各参数

由图4可知，砂轮架系统各阶振型均为平移-扭转组合振动，其中低阶振型以扭转振动为主，高阶振型以平移振动为主。

3 参数灵敏度分析

3.1 固有频率对质量和转动惯量的灵敏度

采用直接微分法推导固有频率对质量和刚度的灵敏度公式为：

(7)

式中：ωr为第r阶固有频率；mλ为模型中的各质量变量；mii为质量矩阵M中第i行第i列的元素；φri为第r阶模态向量中第i个元素；kλ为模型中的刚度变量；kij为刚度矩阵K中第i行第j列的元素。

由式(7)可以计算固有频率对各参数灵敏度的值，结果见表2。

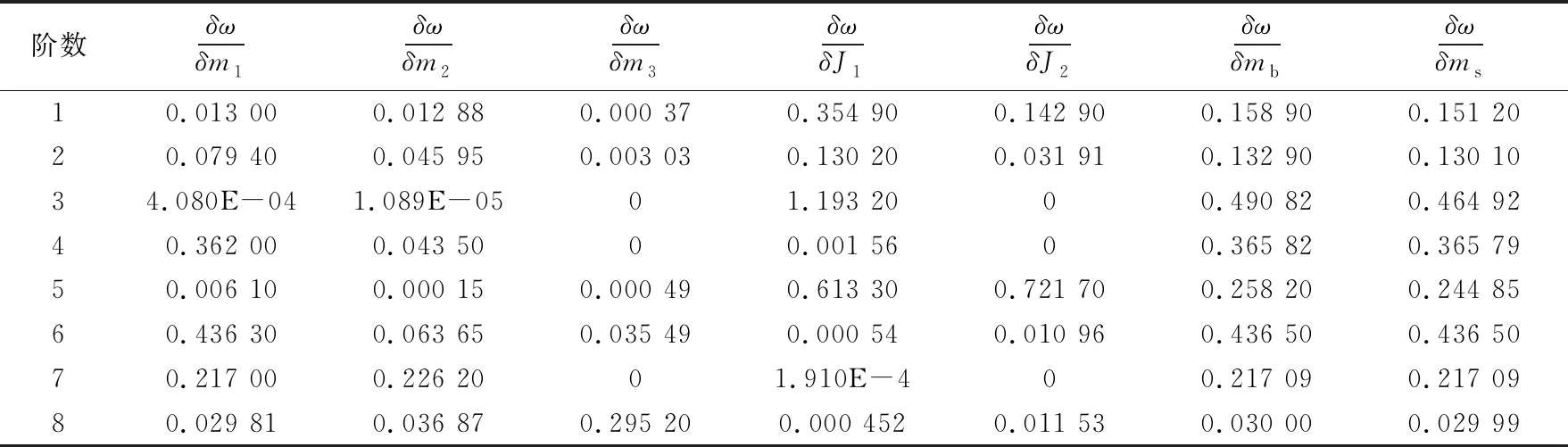
表2 固有频率对质量和转动惯量灵敏度

由表2可知：1)各阶频率对质量参数均比较敏感，其中对砂轮法兰和带轮组件更敏感。另外，砂轮法兰和带轮组件的质量对平移振动和扭转振动都有影响，但对主轴箱的扭转振动没影响；2)系统的扭转振动取决于砂轮架转动惯量，主轴扭转振动和主轴箱扭转振动均对其转动惯量最敏感。

绘制固有频率随参数变化曲线，验证灵敏度分析结果。以砂轮法兰质量对固有频率影响曲线为例进行分析，如图5所示，其余参数影响的分析方法相同，不在赘述。图中曲线从上至下模态阶数依次递减，最上方为第8阶模态，最下方为第1阶模态。

由图5可知，随着砂轮法兰质量增加，第2,8阶固有频率变化较小，其余各阶频率变化较大。当砂轮法兰质量小于750 kg时，第5,7阶固有频率曲线变化较大；第3,4阶及第6阶固有频率曲线，随砂轮法兰质量变化幅度均较大曲线分析结果和灵敏度分析结果相符。

图5 砂轮法兰质量对固有频率的影响曲线

分析各参数灵敏度和影响曲线，可得出以下结论：1)减小砂轮法兰质量可以有效降低多数振型的固有频率；2)减小主轴箱质量可以降低高阶固有频率。

3.2 固有频率对刚度参数的灵敏度的影响

固有频率与各刚度参数灵敏度值见表3。

由表3可知：1)锥面液体静压轴承刚度k1和k2对各阶固有频率均有影响；2)液体V-平静压导轨V形导轨支撑刚度k6主要影响主轴和主轴箱的平移振动，平端静压导轨支撑刚度k7影响拖板平移振动。

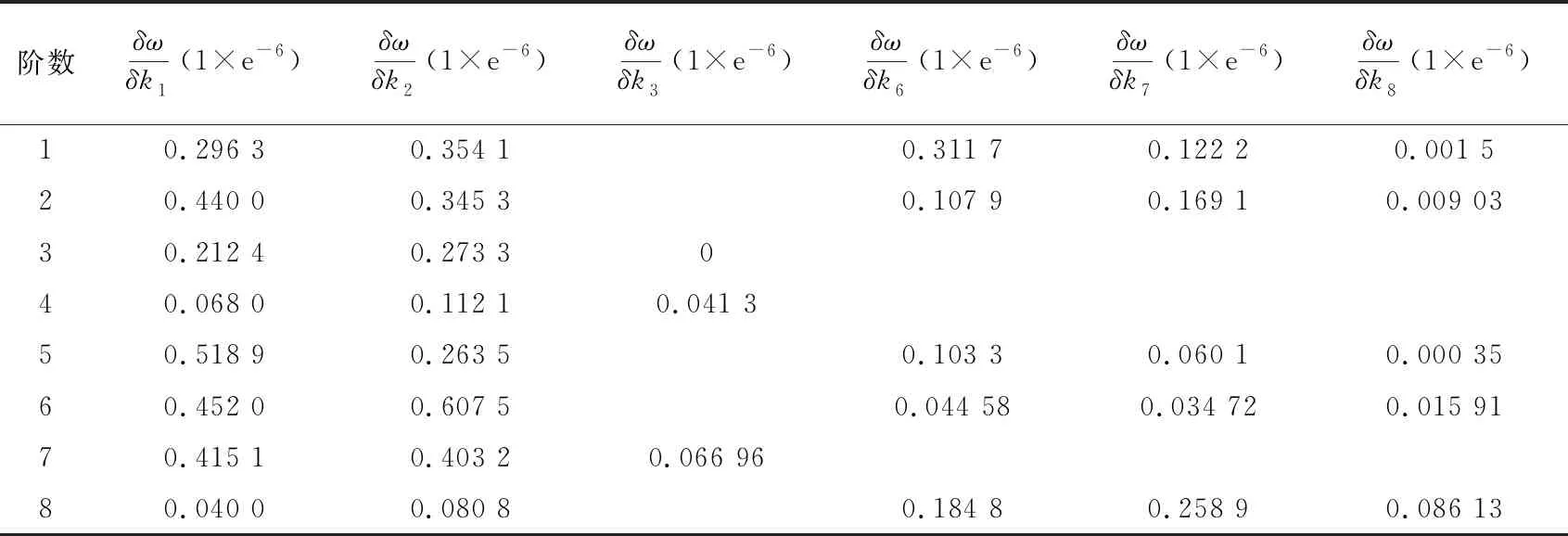
表3 固有频率与刚度参数灵敏度

固有频率随锥面液体静压轴承刚度k1变化的曲线如图6所示。其余刚度参数变化曲线分析方法相同，此处不再赘述。

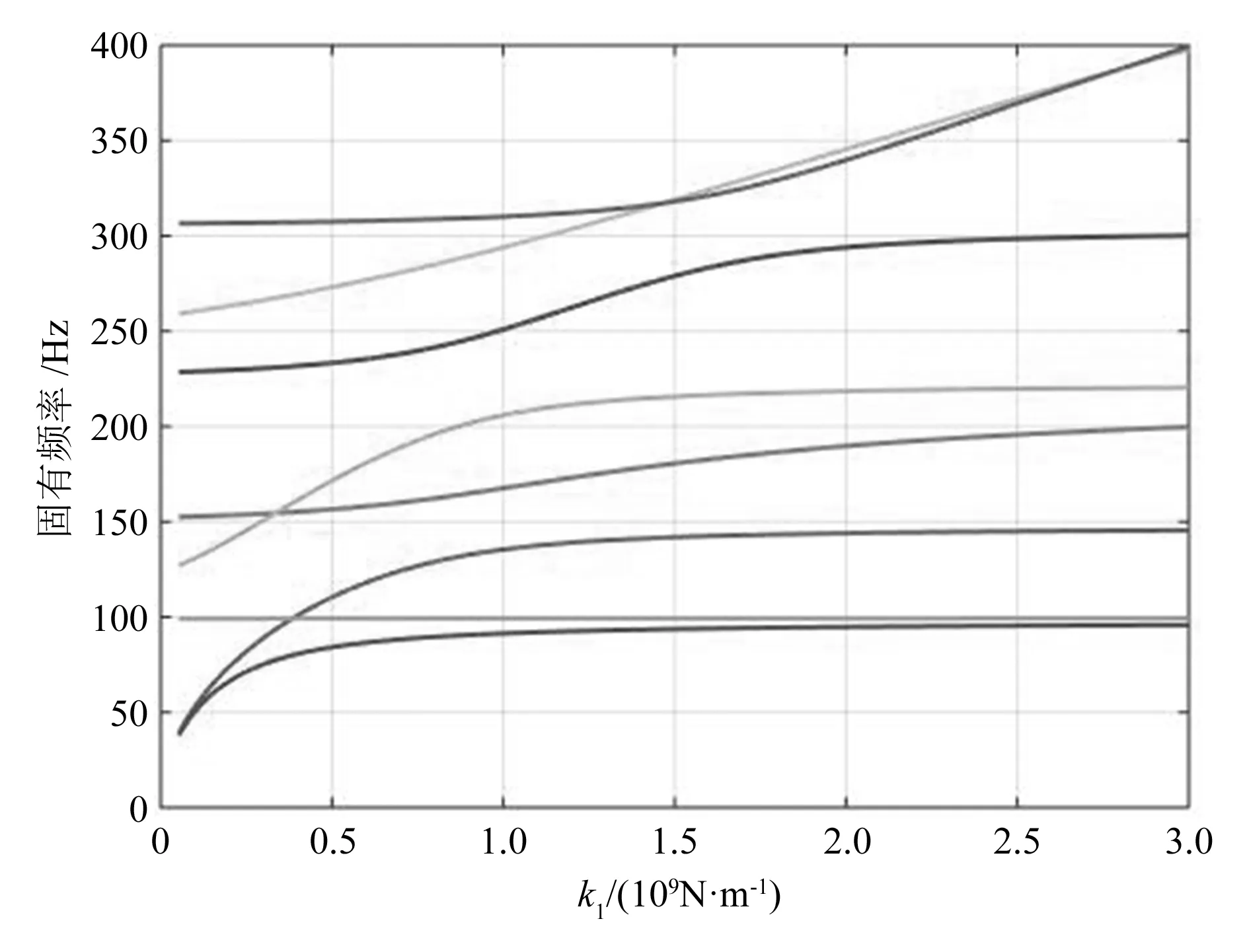
图6 固有频率随k1变化曲线

由图6可知，轴承刚度对多阶模态频率影响较大，且对各阶次影响程度不同。当轴承刚度值处于较小区间时，第1,2,4阶固有频率大幅提升，随着轴承刚度继续增加，这3阶固有频率曲线趋于平缓；第5,6阶固有频率曲线在刚度值前后两段较平稳，而在刚度值中部区间上升较快；第8阶频率在初始时较平缓，在刚度取值较大时上升明显。由此可知，提高锥面静压轴承刚度，可以提升多阶模态频率。

综合各参数灵敏度分析结果，可得出系统动态特性修改方案：

1)减小砂轮法兰质量、增加锥面静压轴承支撑刚度，可全面提高各阶固有频率。

2)减小主轴箱质量和拖板质量，可提高系统高阶固有频率，调整V-平静压导轨支撑刚度，可提高系统低阶固有频率。

3)修改主轴转动惯量可在一定程度上降低砂轮架系统的扭转振动。

通过以上方案优化后，再次计算砂轮架系统各阶固有频率。优化前后固有频率见表4。

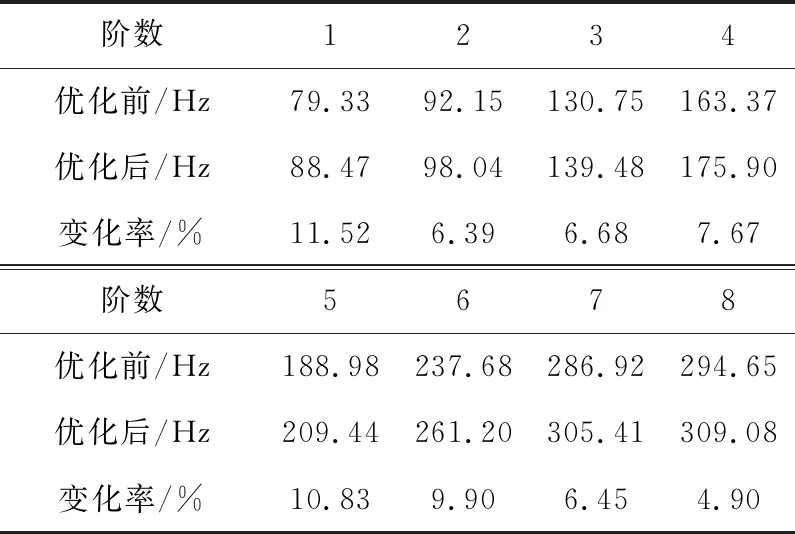
表4 优化前后系统各阶固有频率

4 结束语

本文以集中参数模型为基础，分析了系统固有特性，并讨论了固有特性对质量、刚度、转动惯量等参数的灵敏度，以此获得了砂轮架动态性能修改方案。优化后系统各阶固有频率平均提高8%，表明该方法可有效地改善砂轮架的固有特性。根据本文建立的结构参数模型，还可以进一步研究静压轴承和导轨阻尼对系统动态特征的影响，另外该参数模型也可用于开展系统减振降噪的研究，从而能够更加深入地分析砂轮架系统的动态特征。