GA-BP神经网络在老人负性情绪预测中的应用
2020-09-03王宇星潘英杰
王宇星,黄 俊,潘英杰
(重庆邮电大学 通信与信息工程学院, 重庆 400065)E-mail:tydch@foxmail.com
1 引 言
中国近十年的老龄化速度极快,越来越多的家庭成为“4∶2∶1”的家庭模式;即四名老人,两名中年人和一名青年,但与此同时我国在养老资源上仍有很大的空缺.目前社会上主要的养老方式有居家养老、机构养老和社区养老三种;其中居家养老是最主要的养老方式,其次是机构养老和社区养老.其中,位于养老机构的老年人由于长时间与家人分离,并且所处环境相较于另外两种养老方式比较封闭,因此更容易出现抑郁、焦虑等负性情绪[1].养老机构对老人心理健康关注度不够是现阶段机构养老方式存在的问题之一.
目前,有不少学者和研究人员通过机器学习方法预测人类的情绪.梅梅和刘颖使用SVM(支持向量机)的方式识别微博的语言情绪并应用到旅游推荐中[2];黄中海使用BP神经网络预测高校学生可能存在心理疾病[3];郝苗苗和徐秀娟等人使用朴素贝叶斯、支持向量机等多种分类方式对中文微博中的情绪进行分类[4].
人类的情绪受各方面因素的影响,因此情绪存在复杂性和多变性[5],传统的线性分类器在预测人类情绪时效果较差;而神经网络模拟人类大脑的运行方式,在非线性的分类问题上表现优秀,适合处理人类情绪的分类问题.但传统BP神经网络也存在收敛速度慢,容易陷入局部最优的缺陷[6];因此本文根据传统BP神经网络的不足,提出利用遗传算法优化BP神经网络的初始权值和初始阈值,建立基于遗传算法优化的BP神经网络预测模型,使得BP神经网络在预测养老机构老年人负性情绪时能够以更快的速度找到全局最优解,同时提高预测精度.
2 算法资料
2.1 BP神经网络
本文中使用的神经网络为多层前馈神经网络[7](Multilayer Feedforward Neural Network),BP(Back-Propagation)是神经网络中调节权值和阈值的一种算法;为了方便起见,后面将统一以BP神经网络代称.该神经网络由输入层、隐藏层(或隐含层)和输出层组成;其主要特点为信号沿“输入层—隐藏层—输出层”的方向正向传播,而信号误差则沿着相反的方向传播.图1是一个通用的三层BP神经网络示意图.
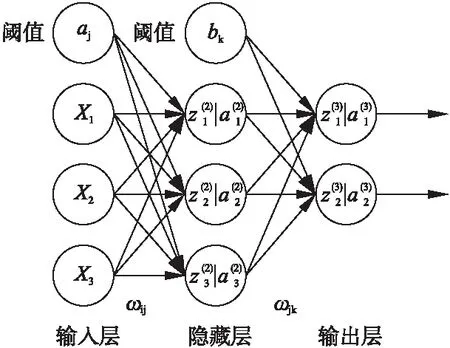
图1 三层BP神经网络
有监督的BP神经网络学习过程如下:
1)初始化神经网络,设置输入层节点个数n,隐藏层节点个数l,输出层节点个数m.输入层到隐藏层的权值ωij,阈值aj;隐藏层到输出层的权值ωjk,偏置bk.学习速率η,设置激励函数g(x),此处激励函数使用Sigmoid函数,形式如公式(1)所示;
(1)
2)计算隐藏层的输出Hj和输出层的输出Ok,计算公式如公式(2)所示;
(2)
3)取误差公式为公式(3),计算误差E;
(3)
4)根据BP(Back-Propagation)算法,为使误差函数达到最小值,本文使用梯度下降法更新权值ωij、ωjk和阈值aj、bk,其中权值的更新公式(4)所示,阈值更新公式(5);

(4)
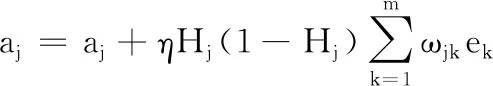
(5)
5)达到预先设定的目标函数值或者最大学习次数m,算法结束.
传统的BP神经网络应用非常广泛,但是为了满足不同的需求,出现了很多改进方案.齐银峰,谭荣建使用改进粒子群算法改进BP神经网络[8],使得BP神经能够以更快的速度收敛;沈夏炯,王龙将人工蜂群算法应用到BP神经网络中,经过优化之后的BP神经网络能够更好的检测网络入侵[9];钟建伟,刘俊夫使用遗传算法优化BP神经网络,在配电网故障定位方面取得进展[10].对于BP神经网络的优化大多都是根据不同应用场景的需求而有针对性的制定;本文在传统BP神经网络拟合结果不理想的情况下,通过分析养老机构老年人负性情绪产生的原因,结合多种优化方式的优缺点,最终选择遗传算法作为优化方式.
2.2 遗传算法
遗传算法(Genetic Algorithm,GA)是模拟达尔文生物进化论中自然选择和遗传学机理的生物进化过程的计算模型,其特点之一是:由于搜索始于解的一个种群,因此能够有效避免陷入局部最优[11].遗传算法能够在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得最优解.遗传算法一般过程为先对种群个体进行编码,初始化种群;然后按照优胜劣汰和适者生存的原理,使用选择函数挑选个体,最后得出结论.交叉和变异在选择时同步进行.
相关名词解释如下:
编码:编码可以理解为将种群中所有个体分别设定唯一的基因组或识别码.编码有三大类:二进制编码、浮点编码和符号编码.此处以二进制编码为例:二进制编码的染色体有“0”和“1”两种碱基.
适应度函数:也被称为评价函数,代表种群中个体被选中的概率,函数值越高则被选中留下的概率越大.
选择函数:选择函数决定存活的个体.常用的选择函数有随机轮盘、精英选择机制等.一般情况下,适应度越高的个体,被选择函数选中留下的几率越大.
交叉:遗传算法中的交叉操作,也被称为基因重组;交叉是使得子代不同于父代的关键步骤之一.不同的编码方式下的交叉操作也不同,此处的编码方式以二进制编码为例,简述交叉操作:二进制编码下的交叉类似生物体的同源染色体联会过程[12],即交换同一位置的编码,产生新的子类.
变异:遗传算法中的变异操作,也被称为基因突变;变异和交叉一样,都会随着编码方式的不同而发生改变.二进制编码的变异操作就是碱基有概率从“0”或“1”变为相反的“1”或“0”.
2.3 基于遗传算法优化的GA-BP神经网络
由于传统BP神经网络存在收敛速度慢,并且不利于全局寻优的缺点,因此本文利用遗传算法优化BP神经网络,建立GA-BP神经网络模型(GA-BP Neural Network Model),预测养老机构中老年人可能存在的负性情绪.主要优化方向为优化BP神经网络的连接权值和阈值,方法为使用遗传算法替代传统的学习方法,克服BP神经网络容易陷入局部最优同时收敛速度慢的缺陷.遗传算法共有4个参数需要提前设定,且较为依赖经验,本文选取遗传算法的参数为:
交叉率:交叉率影响种群更新的效率.过大会破坏已有的有利模式,错失最优个体,过小不能有效更新种群;本文选取交叉率为90%.
变异率:变异率影响种群多样性下降速率.变异率过小会导致多样性下降过快,有缺陷的基因迅速丢失且不容易修补,过大则会导致高阶模式的破坏概率增大;本文选取变异率为0.8%.
种群规模:种群规模太小会造成病态基因的出现概率增加,不利于种群进化,太大会造成难以收敛且浪费资源;本文选取种群规模为50.
进化终止代数:终止代数主要影响种群的成熟度.过小的终止代数会导致算法还未收敛,过大的终止代数可能造成过拟合现象;本文选取终止代数为100.
利用遗传算法优化的GA-BP神经网络的具体流程为:
1)初始化遗传算法的各项参数.
2)初始化种群,对结构进行编码,随机生成N个个体,每一个个体代表一个神经网络.
3)将当前代的个体解码,按照解码结果构造神经网络.
4)使用预设的神经网络参数和随机的连接权值训练神经网络.
5)根据训练结果计算每个个体的适应度,选取若干最优个体,将基因保留到下一代.
6)使用交叉、变异等处理方法,处理当前代种群,并生成下一代种群.
7)重复步骤3到步骤6,直到满足终止条件.
8)利用遗传算法得到的最优个体初始化BP神经网络的权值和阈值.
9)开始训练BP神经网络,直到满足终止条件.
利用遗传算法优化GA-BP神经网络的示意图如图2所示.
3 案例分析
本文选取北京大学开放研究数据平台的中国健康与养老追踪调查数据空间(CHARLS)中2008年的追踪数据作为研究数据,通过去除重复值、数据归一化和中心化等处理,按照一定比例划分训练集和测试集.
3.1 数据清洗以及输入、输出项的选择
中国健康与养老追踪调查数据空间(CHARLS)中2008年的追踪数据共有3047个特征项,包含16954项个案,本文仅采用部分特征项作为输入项.其中,特征项的选择采用单总体T检验对输出的负性情绪在所有特征项上进行考察,选取具有正向预测效果的特征项,其中统计量t和样本标准偏差s计算公式如公式(6)和公式(7)所示:
(6)
(7)
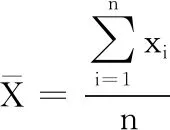
通过单总体T检验最终选出41项特征项作为输入项,包括性别,年龄,受教育年限等;输出项采用人工筛选的方式,选取数据集中已标识的5个负性情绪作为输出项,分别为:害怕、焦虑、孤单、悲伤和沮丧.
最终,数据集通过去除重复值、数据归一化和中心化等处理,筛选出9889项个案.其中归一化的计算公式如公式(8)所示:
(8)
公式(8)中的xi和xj分别为归一化之前和归一化之后的特征项,xmax和xmin代表该数据空间中xi对应特征项的最大值和最小值.
3.2 隐藏层节点数的确定
在神经网络初始化的过程中,为了避免隐藏层节点数目过多出现过拟合现象,部分学者采用公式(9)确定隐藏层节点数:
(9)
其中,Nhid为隐藏层节点数,Nin为输入层节点数,Nout为输出层节点数,α∈[1,10].本文中,根据输入项数目和输出项数目确定隐藏层节点数范围为[8, 17];为挑选最优的隐藏层节点数,本文采用均方根误差(Root Mean Square Error,RMSE)作为衡量指标。RMSE的计算公式如公式(10)所示:
(10)
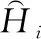
现将所有的GA-BP神经网络模型独立运行10次,得出隐藏层节点数和RMSE的关系如图3所示.由图3可以看出,当隐藏层节点数为11时,每种负性情绪预测模型输出的RMSE都能够取得最小值,说明此时GA-BP神经网络的性能最优.
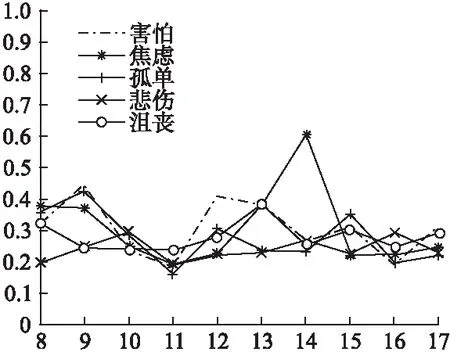
图3 RMSE与隐含层节点数的关系
4 结果分析
为比较不同神经网络在本文选取数据集上的性能差异,笔者选取了基于粒子群优化的PSO-BP神经网络和传统BP神经网络作为对比神经网络,比较两种神经网络与基于遗传算法优化的GA-BP神经网络在性能上的差异.神经网络的部分预设参数取自经验参数,部分参数根据不同优化算法获取.神经网络的学习率取为0.025,迭代次数取为200,隐藏层节点数取为11.
首先比较三种神经网络在不同训练集比例下的性能差异,现分别选取10%到90%的数据作为训练集,将三种BP神经网络独立运行10次,以均方根误差(RMSE)作为衡量指标,得到对比图如图4所示.
从图4中可以看出,随着训练集比例的上升,RMSE不断下降,说明训练数据集的增加提高了预测的准确性;同时GA-BP神经网络在相同比例训练集下的RMSE比传统的BP神经网络更低,与PSO-BP神经网络数据接近,说明GA-BP神经网络和PSO-BP神经网络在性能上相较于传统BP神经网络有较为明显的提升.

图4 三种神经网络在不同比例训练集下的对比
然后对比三者的收敛速率.为比较GA-BP神经网络、PSO-BP神经网络和传统BP神经网络在收敛性上的差异,此处选择均方误差(MSE)作为目标函数,均方误差计算公式如公式(11)所示:
(11)
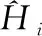

图5 收敛性能比较
从图5可以看出,PSO-BP神经网络在收敛速度上优于GA-BP神经网络与传统BP神经网络,这是由于遗传算法的染色体之间共享信息,整个种群的移动是比较均匀的向最优区域移动.粒子群算法中的粒子是通过当前搜索到的最优点进行共享信息,整个搜索过程是跟随当前最优解的过程[13].因此在绝大多数情况下,粒子群算法比遗传算法有更快的收敛速度.
最后比较三者在准确性上的差异.现将所有预处理后的数据按照4∶1的比例划分为训练集和测试集,分别对5种负性情绪进行建模和预测.表1是三种BP神经网络在5种负性情绪上的准确性对比.
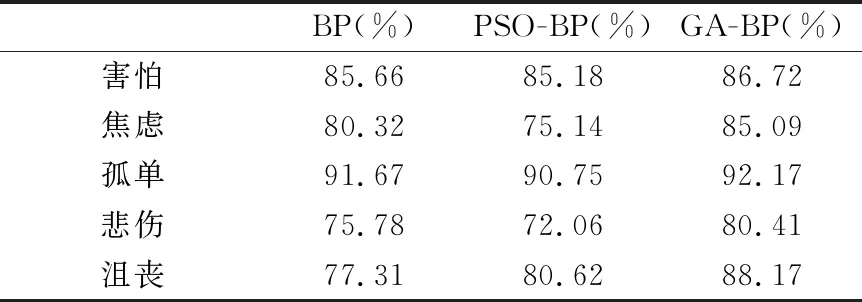
表1 三种神经网络准确性对比
由表1可以看出,在预测害怕和孤单时,三种BP神经网络的差异并不明显,但是在预测另外三种负性情绪时,GA-BP神经网络相较于其余两种神经网络在准确性上有较为明显的提升,说明GA-BP神经网络对老年人负性情绪的预测在准确性上有较为良好的表现.
5 结 语
在传统的BP神经网络中,权值和阈值的初始值对于BP神经网络的全局寻优和收敛速度有极为重要的意义[14].为了提高BP神经网络的全局寻优能力和收敛速度,本文分别选取了遗传算法和粒子群算法作为提高BP神经网络全局寻优能力和加快收敛速度的优化方案.结果证明,粒子群算法和遗传算法都能够提升BP神经网络的收敛速度,同时避免陷入局部最优;粒子群优化的PSO-BP神经网络在收敛速度上更快,遗传算法优化的GA-BP神经网络在准确度上更优.考虑到养老机构对于数据实时性要求不高,因此选取遗传算法作为BP神经网络在负性情绪预测上的优化方案是目前阶段较为良好的选择.但是由于数据集限制,目前只能对5种负性情绪建模;后续工作将在养老机构中实地调研数据,同时继续学习BP神经网络的优化方式,进一步完善养老机构老人的负性情绪预测系统.
