基于奇异值分解改进观测矩阵的FBG传感信号处理
2020-09-02刘航王波郎代志
刘航 王波 郎代志


摘 要:针对地下管廊环境恶劣复杂、噪声干扰较大的问题,提出一种基于奇异值分解的改进观测矩阵方法,通过提高压缩感知处理光纤布拉格光栅传感信号精度,完成噪声预处理。对观测矩阵进行分解重构,提高信号重构保真度。首先对随机观测矩阵进行正交化处理,再对其进行奇异值分解,将特征矩阵特征值改为恒定值,带入新的特征值后将产生新的观测矩阵。对信号进行观测,并采用信噪比、重构误差等指标确定稀疏度K。仿真结果表明,该方法重构精度提高约72%。
关键词:压缩感知;奇异值分解;观测矩阵;传感信号
DOI:10. 11907/rjdk. 192419 开放科学(资源服务)标识码(OSID):
中图分类号:TP393文献标识码:A 文章编号:1672-7800(2020)008-0202-05
Abstract: Aiming at the problem of large noise interference in the harsh complex environment of underground pipe gallery, we propose an improved observation matrix method based on singular value decomposition(SVD) to improve the accuracy of the compression sensing (CS) processing fiber Bragg grating sensing signal and achieve the purpose of noise preprocessing. The signal reconstruction fidelity is improved by decomposing and reconstructing the observation matrix. Firstly, the orthogonal observation matrix is orthogonalized, and then the singular value decomposition is performed. The eigenvalue of the feature matrix is changed to a constant value, and a new eigenvalue is generated to generate a new observation matrix to observe the signal. The SNR and reconstruction error are used to simulate and evaluate. The results show that the reconstruction accuracy of the proposed algorithm is improved by about 72%.
Key Words: compressed sensing; singular value decomposition; observation matrix; sensing signals
0 引言
随着我国城市化进程的加快,地下管廊设施规模建设逐渐庞大、密集,结构布局复杂,安全监管诉求十分迫切[1-3]。地下管廊因处于封闭的高湿恶劣环境,传感器稳定性差、寿命短、运维频繁。光纤传感器因其耐腐蚀、抗电磁干扰等优点被广泛应用于煤矿矿井安全检测[4-5]、地面沉降监测[6]、地下管廊等方面。由于应用环境恶劣,FBG传感信号在采集和传输过程中容易引入噪声,从而使信号后期分析更困难。因此,对被噪声污染的信号进行去噪预处理显得尤为重要。
小波去噪因其多尺度、多分辨率特性在信号处理领域受到广泛关注,但小波去噪效果受小波基、分解尺度、阈值和阈值函数影响,处理效率有限,若影响参数选择不合理将导致较大的重构偏差[7]。江虹等[8]采用小波处理FBG传感信号,得到的光谱图仍有较多毛刺;经验模态分解(Empirical Mode Decomposition,EMD)可根据信号频率特性将其自适应地分解,但耗时长,且无法将分布于整个频域的噪声与信号有效分离[9-11]。压缩感知(Compressed Sensing,CS)理论利用信号稀疏性和可压缩性,以较少的采样数据恢复原始信号,在采样同时完成数据压缩。通过非线性重构算法对采集得到的信号离散样本数据进行重构,恢复原始信号。相比于传统Nyquist采样,CS采样成本低、效率高,并在数据传输和存储过程中大幅提高了资源利用率。该理论主要包括3方面:信号稀疏度估计、观测矩阵设计及重构算法。陈勇等[12]提出多指标融合确定稀疏度,文献[13]采用相关系数变化规律确定稀疏度。观测矩阵设计方法主要有随机观测、确定性观测和自适应观测3种[14-18],王志文等[19]以高斯随机观测矩阵为基础,利用信号稀疏域的先验信息设计自适应观测矩阵,减少观测矩阵行数,降低了传输代价;彭玉楼等[20]对观测矩阵进行奇异值分解,并通过均值算法修改特征值产生新的观测矩阵,提高了信号重构精度。除观测矩阵外,重构算法也是影响去噪效果的因素之一,常用重构算法有凸优化算法和贪婪迭代算法两大类。凸优化算法把l0范数放宽至l1范数,通过线性规划求解,计算复杂度大,如梯度投影算法、基追踪算法等;贪婪算法通过选择合适的原子逐渐实现矢量逼近,算法结构简单,复杂度低,如正交匹配追踪算法(OMP),该算法以稀疏度K已知为先验条件,K值选择在很大程度上影响算法性能。因此,重构算法与观测矩陣设计是影响压缩感知性能的两个关键因素。
本文在文献[21]的观测矩阵设计方法基础上进行改进,以随机观测矩阵为基础,首先对观测矩阵进行正交处理,再通过奇异值分解将奇异值设定为恒定值,得到新的观测矩阵。通过考虑多指标的综合性能确定稀疏度K并采用OMP算法重构信号。仿真结果表明,本文算法重构信号性能更优。
1 CS理论基础
CS理论指出,若给定信号在某个变换域下是稀疏的,可通过一个与其不相干的观测矩阵将信号投影到低维空间上,再通过求解优化问题从低维信号中高概率地恢复原始信号[22-23]。
实常数[ω]始终为1的倍数,将奇异值置为实常数。由正交矩阵奇异值分解特性可知,该操作保证空间几何度量不变的同时,避免了所选原子信息特征冗余,使其构成的支撑集更加准确,从而提高信号重构精度。
3 OMP重构算法
贪婪迭代算法结构简单,计算量小,是求解式(2)得到原始信号最优逼近的恰当选择。OMP算法是贪婪迭代算法的典型代表,其核心思想是每次迭代选择与残差信号相关性最大的一个原子,通过多次迭代求解最优逼近,从而达到消除干扰噪声的目的。算法迭代次数K的选择是关键,即从库中选择K个与原始信号相关性最大的原子重构信号。
算法步骤为:
(1)输入:M×N维观测矩阵Φ,稀疏度K,观测向量y。
(2)输出:x的K稀疏逼近x。
(3)初始化:残差res=y,索引集[J0= ],支撑集[Λ0= ],t=1。
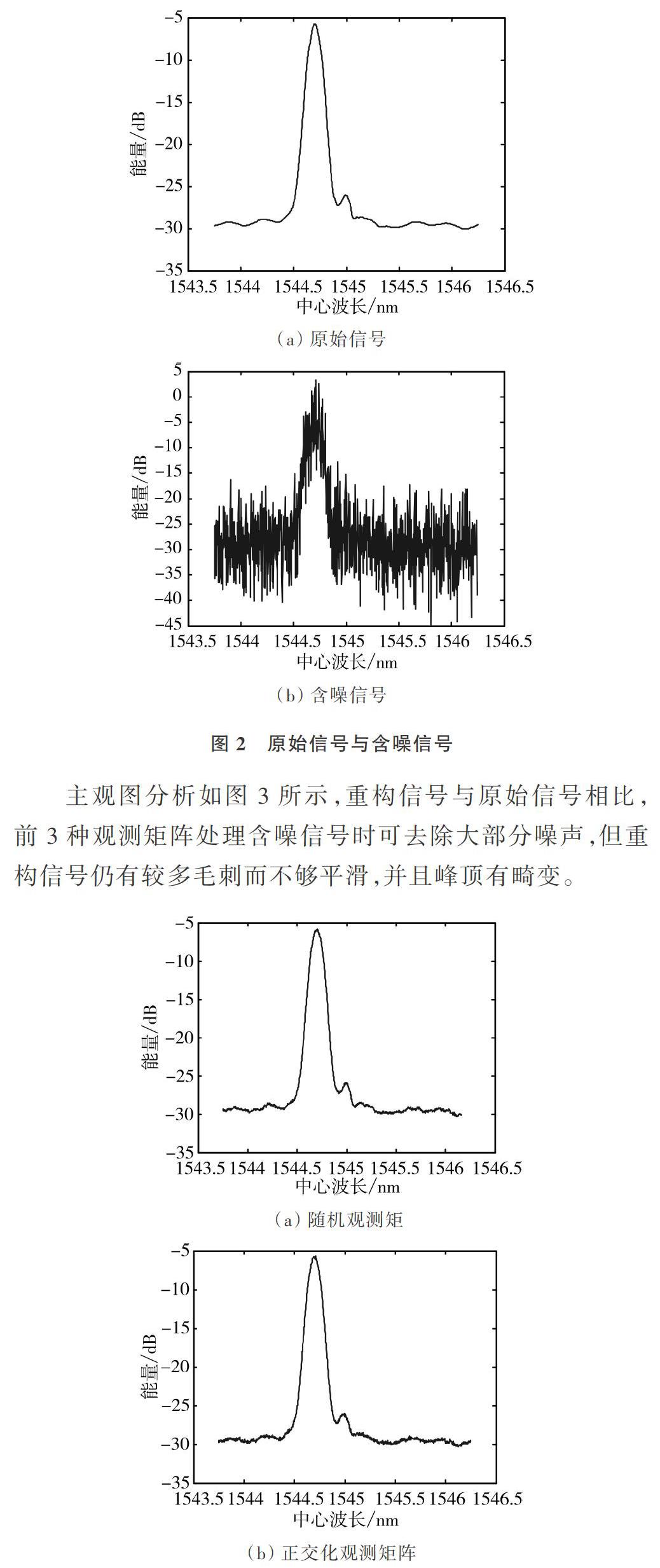
(4)循环执行:①计算第t次迭代[ut|ut= 从以上步骤中可知,OMP算法需先确定迭代次数,即K值。然而,FBG传感信号稀疏度K是未知的。 4 仿真验证 4.1 评价指标 为验证本文方法,分别对一维信号和二维信号进行去噪处理。在MATLAB软件环境下进行实验仿真,仿真重构算法选取经典匹配追踪算法(OMP),分别采用4种不同的观测信号:随机观测矩阵、正交处理的观测矩阵、文献[9]方法及本文提出的观测矩阵。 一维信号去噪的评价指标为信噪比(SNR)和均方根误差(RMSE)。SNR值越大且MSE值越小,说明去噪效果越好。SNR与RMSE如式(12)、(13)所示。 从图1可知,随着横坐标K值跨度从10到100,以步长为10不断增大,SNR总体呈上升趋势,而RMSE总体呈现下降趋势,并在K=80时分别达到最大和最小。原因在于随着K过小时选择的原子数太少而无法较好地恢复信号,从而丢失了细节信息;而K值过大容易导致数据冗余,恢复部分噪声。因此,K值过小或过大均会导致SNR较小而RMSE较大,只有恰当的K值才有助于信号恢复。 4.3 信号仿真及对比 采用Matlab软件仿真平台对本文算法进行一维信号仿真验证,实验信号为FBG传感信号,中心波长[λ=1 544.70],信号长度[N=1 000],压缩比[MN=0.4],稀疏度[K=80]。图2(a)、(b)分别为原始FBG信号与加入了15dB高斯白噪声的含噪信号。采用随机观测矩阵、正交化观测矩阵、文献[9]中提出的矩阵与本文观测矩阵,分别处理加入15dB高斯白噪声的测试信号,并通过OMP重构算法得到重构信号,如图3(a)-(d)所示。 主观图分析如图3所示,重构信号与原始信号相比,前3种观测矩阵处理含噪信号时可去除大部分噪声,但重构信号仍有较多毛刺而不够平滑,并且峰顶有畸变。 由于观测矩阵是随机生成的,观测采样后得到的观测值也不一样,因而每次重构信号的精度均存在细小波动,需多次实验取其平均结果。图4为设置的奇异值常量与信号重构误差关系,随着常量值的增大,重构误差逐渐缩小,且当常量值为60时,重构误差趋于稳定。因此,设置奇异值常量为60处理含噪信号。从图5的处理结果可知,选择本文设计的观测矩阵得到的信噪比最大。其中,横坐标为噪声含量,纵坐标为去噪后的噪声含量(SNR),SNR越大说明噪声含量越少。利用4种观测矩阵对图1(b)的含噪信号处理后得到的数据结果如表1所示,通过对比分析可知,本文观测矩阵处理信号得到的重构精度最高,得到的SNR最大且RMSE最小,分别为52.175 9dB和0.046 3。 对于二维图像信号,采用Lena图像作为实验信号,图6(a)、(b)分别为原始图像和加入密度为0.02的椒盐噪声含噪图像。采用4种不同观测矩阵处理含噪图像得到的结果如图5(c)-(f)所示。从表2分析可知,本文方法处理图像得到的峰值信噪比最大,为26.092 8,说明去噪效果最好。 5 结语 FBG传感信号采集和传输过程中不可避免地会引入噪声,采用压缩感知的方法进行去噪预处理。对随机生成的观测矩阵首先进行正交处理,再采用奇异值分解修改正交化的观测矩阵。仿真结果表明,与其它观测矩阵相比,本文观测矩阵基于改进压缩感知理论使信号在观测中保留更细节的特征,与其它算法相比,得到的重构信号SNR更大,去噪效果更好,但在算法时效性上还有提升空间。 参考文献: [1] 侯得林. 城市地下管廊结构变形缝止水工法[J]. 科技创新与应用, 2017(9):253-253. [2] 周刚基. 基于光纤传感技术的城市地下管廊综合监控系统的应用及发展[J]. 中国安防, 2015(24):26-30. [3] 劉敏敏, 周峰, 杜志顺,等. 光纤传感器在石油测井中的应用[J]. 光学与光电技术, 2008, 6(3):18-21. [4] 杨洋, 杨哲. 光纤检测在石油勘探中的测量优化设计研究[J]. 中国仪器仪表, 2014(10). [5] 侯培虎, 付晓宁, 王颖,等. 矿井光纤物联网云连接平台技术的研究[J]. 山东科学, 2011, 24(2):41-46. [6] 方文浩, 关涛, 叶炜,等. 面向地面沉降长期自主监测的分布式光纤物联网系统[J]. 上海国土资源, 2014(4):85-89. [7] 王维博,董蕊莹,曾文入,等. 基于改进阈值和阈值函数的电能质量小波去噪方法[J]. 电工技术学报, 2019, 34(2):409-418. [8] 江虹, 苏阳, 李进等. 一种小波阈值去噪在FBG解调中的改进方法[J]. 光通信研究, 2016(2):40-43. [9] ROHILA A. ECG signal denoising by empirical mode decomposition[C]. International Conference on Emerging Trends in Electrical, Electronics and Sustainable Energy Systems, 2016:308. [10] 王杰华, 夏海燕, 孙万捷,等. 基于EMD和SVD的光电容积脉搏波信号去噪方法[J]. 现代电子技术, 2018, 41(4):65-69. [11] 王星. 基于EMD的分布式光纤管道测温信号去噪分析[J]. 电脑与电信, 2019, 269(3):51-54. [12] CHEN Y,ZHANG Y, LIU H L, et al. FBG sensing signal dealing with improved orthogonal subspace pursuit method[J]. Optik-International Journal for Light and Electron Optics,2015,126(21):3303-3309. [13] 陈勇, 张玉兰,刘焕淋,等. 改进的多原子匹配追踪算法处理FBG信号[J]. 光电子·激光, 2016(6):580-586. [14] 赵玉娟, 郑宝玉, 陈守宁. 压缩感知自适应观测矩阵设计[J]. 信号处理, 2012, 28(12):1635-1641. [15] 邓小炼, 王星, 艾思敏,等. 奇异值分解和阈值分割的遥感自适应变化检测[J]. 测绘科学, 2016, 41(8):38-42. [16] 孔英会, 胡启杨. 一种改进K-奇异值分解稀疏表示图像去噪算法[J]. 科学技术与工程, 2018, 18(1):287-292. [17] 李周, 崔琛. 压缩感知中观测矩阵的优化算法[J]. 信号处理, 2018, 34(2):201-209. [18] 张春妹. 压缩感知观测矩阵及重构算法的智能优化策略设计[D]. [19] 王志文, 徐以涛, 黄鑫权,等. 基于观测矩阵优化的自适应压缩宽带频谱感知[J]. 通信技术, 2016, 49(1):62-67. [20] 彭玉楼, 何怡刚, 林斌. 基于奇异值分解的压縮感知噪声信号重构算法[J]. 仪器仪表学报, 2012, 33(12):2655-2660. [21] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306. [22] 裴立业, 江桦, 麻曰亮. 基于选择性测量的压缩感知去噪重构算法[J]. 通信学报, 2017, 38(2):106-114. [23] 黄胜强. 基于压缩感知去噪算法在地震勘探随机噪声压制中的应用[D]. 东北石油大学, 2016. [24] 桑雨, 高树生, 宋宏文,等. 利用奇异值分解方法提高地震数据信噪比[J]. 石油地球物理勘探, 2014, 49(增刊1):72-75. (责任编辑:江 艳)
