基于直接配点法的智能汽车避障路径规划研究

薛国号，陈巧玉，许银胜，叶 杰

( 华南理工大学汽车零部件技术国家地方联合工程实验室，广东 广州 510640)

0 引言

避障路径规划是智能汽车控制的一项关键技术。对于智能汽车的避障路径规划而言，要解决的问题可概括为以下3点：能实现汽车从起始位置到目标位置的过程；整个行驶过程中智能汽车能避开所有障碍，安全行驶；使用最优或近似最优的行驶路径[1-4]。

目前，学者们对智能汽车避障路径规划问题开展了大量研究工作[5-9]。传统的人工势场法易陷入局部最小值的困境[10]。基于随机采样的概率路图法具有规划出来的路径不平滑等缺点[11]。以遗传算法和蚁群算法为代表的智能优化算法整体上极大改进了传统避障算法的缺点，但其对计算机硬件的要求较高，在普通车辆上难以大规模应用。高斯伪谱法在路径规划领域以其较快的收敛速度和较高的收敛精度而具备较大优势[12]。

本文基于伪谱法的“离散优化”思想，将在航空航天领域已广泛应用[13]的直接配点法运用到智能汽车避障路径规划问题的求解中。

1 智能汽车避障路径规划建模

1.1 车辆运动学模型

采用包含侧向运动、横摆运动的二自由度二轮车模型作为智能汽车的运动学模型，并以车辆后轴中心的坐标(x,y)表示车辆位置O，所构建的车辆运动学模型如图1所示。图1中，(x,y)为车辆后轴中心位置坐标；(xf,yf)为车辆前轴中心位置坐标；θ为车辆横摆角；δ为前轮转向角；L为车辆轴距；υ为车速。

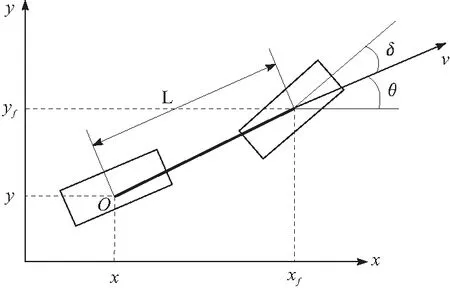
图1 二自由度车辆运动学模型

构建二自由度车辆运动学模型前，提出以下假设：忽略车辆转向系统的动力学特性，以前轮转向角作为转向系统的输入；忽略悬架系统的作用，不考虑垂向及俯仰运动。

智能汽车的非线性运动学模型可表示为

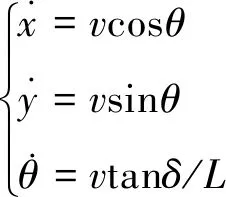
(1)

车辆行驶过程中不仅受到运动学约束，同时也受到转向系统的机械约束，转向角应限制在一定的范围之内。故引入转向角的不等式约束：

δmin≤δ≤δmax

(2)

δmin和δmax分别为转向系统机械约束的最小和最大转向角。同时假定车辆行驶过程中，其速度大小保持恒定，且为v0，即：v=v0

1.2 道路可行驶区域模型

智能汽车在每条车道宽为h的双车直道上行驶，由于直道两边路沿的约束，车辆的可行驶区域可以看成一个尺寸为l×2h的矩形，如图2所示。同时假设车长为a，车宽为b，以尺寸为a×b的矩形刻画智能汽车的边界轮廓，并以矩形的几何中心代表智能汽车的位置O(x,y)。

车辆的行驶区域左边界横坐标为—l/2，右边界横坐标为l/2，因此可得到智能汽车位置O(x,y)约束条件为

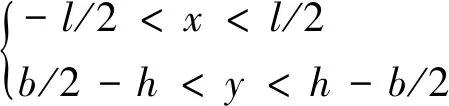
(3)

双车直道车辆可行驶区域如图2所示，图2中阴影部分即表示智能汽车位置O所满足约束条件的区域。

1.3 障碍车辆边界模型

假设障碍车量的尺寸及形状与智能汽车的尺寸及形状一致，障碍车的尺寸如图3a所示，障碍车辆车长a，车宽b。可将障碍车进一步简化为如图3b所示的长为a、宽为b的矩形。如图3c所示，可进一步将障碍车辆简化为以车宽b为直径的车头圆和车尾圆，且2个圆分别与障碍车的矩形边界相切。最终，障碍车边界模型可简化为如图3d所示的半径为b/2、圆心相距a-b的车头圆和车尾圆。

图2 双车直道车辆可行驶区域示意

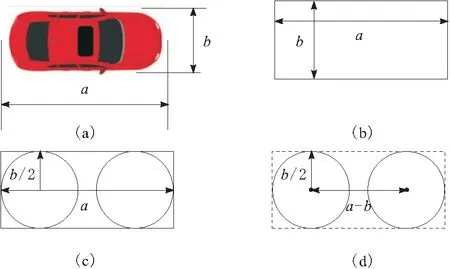
图3 障碍车辆的边界模型

1.4 避免碰撞的临界条件

(4)

为保证智能汽车行驶过程中与障碍车绝对不发生碰撞，智能汽车质心O至车头圆与车尾圆圆心的距离必须大于SOb′+ε(ε为预留阈值)。故可引入智能汽车避免碰撞的约束条件为

(5)

图4 车辆不发生碰撞的临界条件示意

2 避障路径规划问题的建立与求解

2.1 避障路径规划问题

选取智能汽车的位置坐标(x,y)及横摆角θ作为状态变量，选取前轮转向角δ作为控制变量，在如图5所示的双移线工况下，智能汽车的初始状态为(x0,y0,θ0)，终值状态为(xf,yf,θf)。由于智能汽车的起始位置与终点位置处于同一纵坐标，故可引入约束条件：y0=yf同时，在起始时刻车辆的横摆角与终止时刻车辆的横摆角相等且均为0，则施加如下约束条件：θ0=θf=0。

图5 智能汽车双移线工况示意

在双移线工况下以智能汽车的避障时间最短为目标，并考虑了车辆运动学约束、转向系统的物理学约束、可行驶道路区域约束及避免碰撞约束条件，将避障路径规划问题归结最优控制问题为

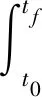
初始条件：x(t0)=x0,y(t0)=y0,θ(t0)=θ0

终止条件：x(tf)=xf,y(tf)=yf,θ(tf)=θf

(6)

2.2 避障路径规划问题的数值求解

2.2.1 时域离散化

将时间区间等间(t0,tf)隔地离散为N个片段(tk,tk+1)，其中k=0,1,2,…,N。将每个阶段的2个端点称为节点，则可得到N+1个节点为

(7)

2.2.2 状态及控制变量的离散化

在(tk,tk+1)的时间区间内，将连续的状态及控制变量在节点处进行离散化处理，并将各时间片段的中点tk+0.5=(tk+tk+1)/2定义为配点。分别在节点及配点处对状态及控制变量离散化，可得到(2N+1)×3个状态变量的离散值和(2N+1)×1个控制变量的离散值。

离散化后的状态变量为

(8)

离散化后的控制变量为

δ=[δ0，δ0.5，δ1，δ1.5，δ2，…，δN-1，δN-0.5，δN]T

(9)

则各阶段内配点处的状态变量可基于节点处的状态通过Hermite插值得到

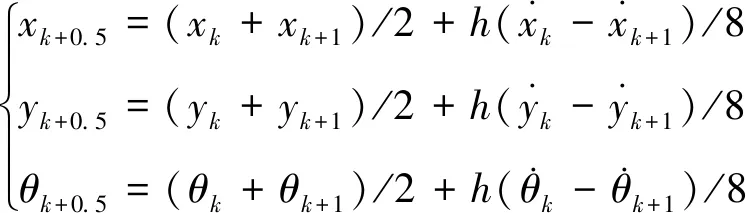
(10)

类似地，配点处控制变量可表示为

(11)

2.2.3 运动学约束的转化

利用三阶Simpson积分公式可得

(12)

则可将运动学方程约束(1)转化为

(13)

2.2.4 目标函数的转化

时间区间(t0,tf)经离散化处理后，可得到N个时间片段。基于此，可将目标函数转化为

(14)

2.2.5 其他约束条件的转化

可将控制变量的约束条件(2)施加于节点及配点处控制变量离散值处，则可得

δmin≤δk≤δmax,k=0,0.5,…,N-0.5,N

(15)

可将道路可行驶区域的约束和碰撞临界约束(即状态变量的约束条件)转化为节点处的状态变量离散值的约束：

(16)

(17)

式(16)和式(17)中，k=0,1,2,3,…,N。

综上所述，通过优化目标、运动学方程约束、转向系统物理学约束、道路可行驶区域约束、碰撞临界条件约束等的转化，可将避障路径规划问题转化为如式(18)所示的非线性规划问题。基于SNOPT对非线性规划问题式(18)的数值求解即可得到节点及配点处的最优状态及控制变量，通过Hermite插值即可获得避障过程中的最优状态和控制变量的轨迹曲线。

(18)

3 仿真分析

在如表1所示的输入条件下，基于配点法对双移线工况的智能汽车避障路径进行规划，所得到的智能汽车路径规划结果分别如图6和图7所示。由图6和图7可知，智能汽车行驶过程中均在道路可行驶区域内，且未与障碍车发生碰撞，最后仍回到原车道实现了双移线避障。

双移线工况下智能汽车避障过程中的车辆坐标、车辆横摆角及车轮转向角的轨迹曲线如图8所示。由图8可以看出，智能汽车避障过程可分为3个阶段。第1阶段(即0～1.2 s)，在开始时刻车轮

表1 车辆双移线工况仿真输入条件

图6 双移线工况下避障路径示意

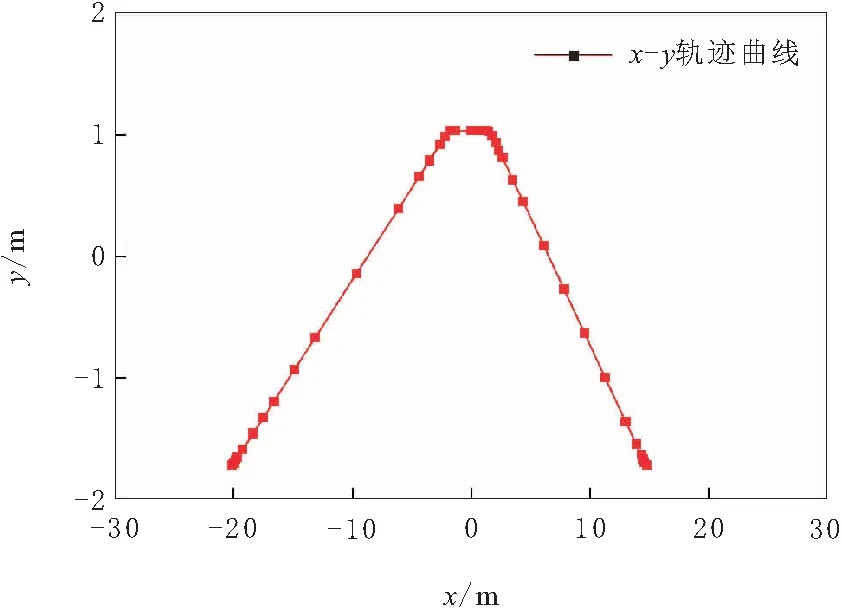
图7 双移线工况智能汽车位置变化曲线

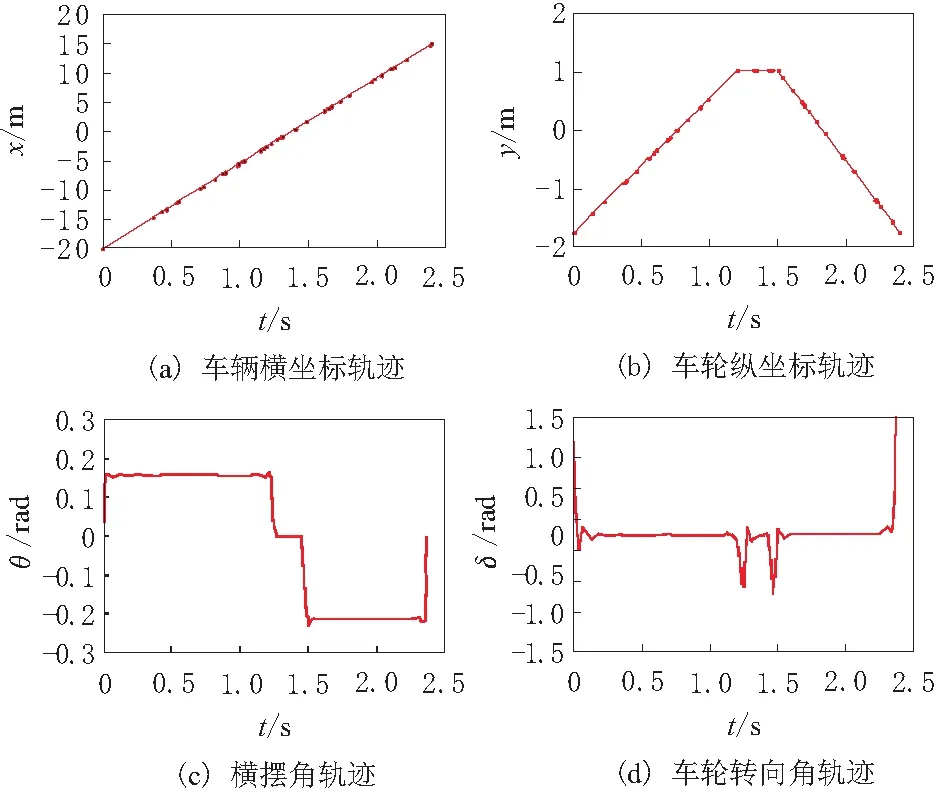
图8 最优状态及控制变量轨迹曲线

转向角有1个突变值(值为1.2 rad)，使横摆角由0迅速升高至0.15 rad，车辆的纵坐标平滑上升，即车辆由原车道行驶至目标车道；且在智能汽车驶至目标车辆，车轮转向角有一个突变值(值为-0.7 rad),使横摆角由0.15 rad迅速减小至0。第2阶段(即1.2～1.45 s)，车轮转向角和横摆角均保持在0，使智能车辆在目标车辆匀速行驶以超越障碍车辆。第3阶段(即1.45～2.4 s),开始时刻车轮转向角有一个突变值(值为-0.75 rad)，横摆角由0迅速减小至-0.24 rad，即使智能车辆由目标车道驶回当前车道；在智能车驶回至原车道，车轮转向角有一个突变值(1.6 rad)，使横摆角由-0.24 rad迅速减小至0，即保证智能汽车在原车道上继续纵向稳定行驶。

上述基于配点法的路径规划算法是在配置为Intel i7，内存16G的Ubuntu18.04系统下基于SNOPT求解器开展的，其求解时间为0.83 s，相较于基于高斯伪谱法的路径规划算法的求解时间(2.90 s)[9]减少了71%。由此可见，基于配点法的避障路径规划算法具有良好的实时性，更适合实际应用。

智能汽车在不同的起始点(即距离障碍车分别为6 m和20 m的起始点)执行双移线避障，目标位置均是，规划所得到的最优避障路径如图9所示。由图9可以看出，不同起始点下的避障路径均能顺利到达目标位置。

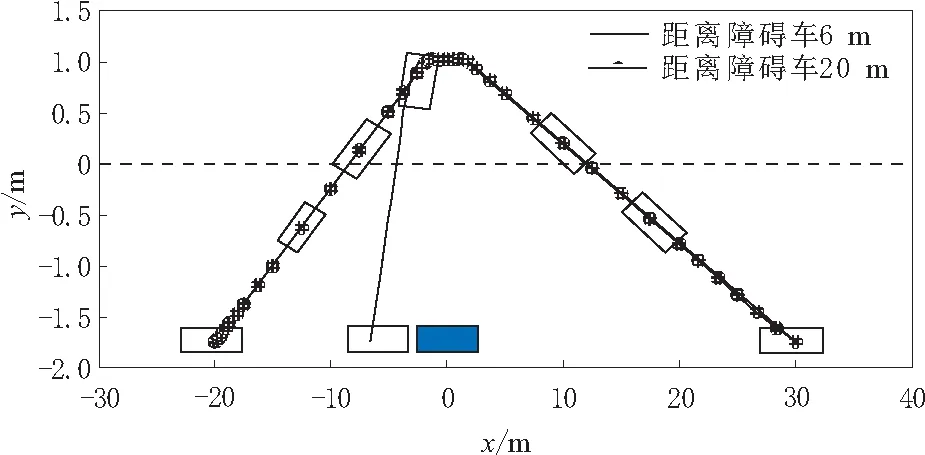
图9 不同起始点的最优避障路径

在不同初始位置且对目标位置不施加约束的条件，智能汽车的最优避障路径如图10所示。由图10可以看出，不同条件下所得到的最优避障路径均平滑过渡，满足约束条件，进一步验证了所提出的路径规划算法的适用性。

图10 不同约束条件下的最优避障路径

4 结束语

构建了智能汽车的简化二轮车模型，并构造了其避障行驶过程中的可行驶区域、避免碰撞的边界约束及物理约束，将双移线工况下的避障路径规划问题归结为最优控制问题。基于直接配点法通过将避障路径规划问题的优化目标、运动学约束及其他约束进行离散化，从而可将其转化为非线性规划问题，并基于SNOPT求解器进行数值求解以获得最优避障路径。数值仿真结果表明：基于直接配点法可较好地规划出平滑的避障路径，且具有良好的实时性和适应性，在实际智能汽车控制中具有良好的应用价值。