基于分布式电源接入的低压台区节点模型抗损研究
2020-09-02刘金亮宋文乐王立宗董成哲
刘金亮,宋文乐,黄 庆,王立宗,董成哲
(1.国网沧州供电公司,河北 沧州 061000;2. 国网河北省电力有限公司沧州 供电分公司,河北 沧州061001;3.北京新源绿网节能科技有限公司,北京101100)
0 引言
线损管理一直是供电领域中的重点工作之一,其对供电行业的经济效益有着直接的影响。随着供电规模的不断扩大的提高,低压台区节点模型线损管理逐渐受到越来越多的关注[1]。
线损是指电力传输过程中所产生的有功电能损失。电能从发电站输送到用户端的过程需要经过不同的输变电元件,这一过程难免会造成一定的电能损失。一方面,电网中各个元件存在电阻和电抗,另一方面,电能在交换过程中需要一定的励磁功率,从而造成电能损失[2]。除此之外,电力设备泄露、计量设备偏差和人为误差等原因也会造成电能损耗。同时,由于低压台区数量较多、缺乏高效的技术手段、管理工作相对落后,导致低压台区配电网络线路节点损耗较大。
目前,分布式电源接入方式以其形式灵活、便捷可靠等特点得以广泛应用。分布式电源一般采用自发自用模式,可以实现功率的就地消纳,继而通过减少功率传输而减少配网的电能损耗。
因此,为有效减少低压台区配电网络线路的节点损耗,基于分布式电源接入方式,设计了一种低压台区节点抗损模型。
1 低压台区节点负荷矩计算
负荷矩代表某一电压损失条件下电力负荷与线路长度的乘积,线路的电压降落与线路的负荷矩成正比。在实际应用中,只能够获取少数节点的电压值,所以能够提供计算的线路电压值[3]较少,甚至存在不能获得的情况,因此为了反映电压值与线路负荷矩的关系,重新对节点的负荷矩进行定义。
在不考虑用户功率[4]的情况下,每条线路的线路负荷矩为
(1)
gj为流过j线路的负荷;d为电网线路距离。
低压配网拓扑结构简化如图1所示。
假设h代表电网j线路中i节点与第一个节点之间线路上的所有节点结合(i为图1中的1,2,3,4,5,6,7,8),则电网中每个节点的节点负荷矩为

(2)
p为电网线路的功率分布参数。

图1 低压配网拓扑结构简化
依据上述过程可知,负荷矩累积一段时间后,线路上的负荷矩[5]也会随之增加,从而增加节点负荷矩。并且节点负荷矩越大节点电压越低,因此将电网中线路负荷矩对电压的影响看做负荷矩对电压的影响,是影响台区配网损耗的直接因素[6]。
2 分布式电源接入下的综合线损率确定
在接入分布式电源后,由于接入系统的差异会产生电量倒送的情况,即负荷会倒送会配电端。若电网难以完全消化负荷时,负荷也会进一步倒送[7]。因此需要从始端向末端计算各个节点电压,其计算流程如图2所示。

图2 电压计算流程
在上述节点电压计算完成基础上,对负荷进行计算,将供电量与实际供电量之间的差值定义为统计线损[8],其计算公式表示为
(3)
Ah代表线损电量,即供给电量与销售电量的差值;Δa为线损率。
在此基础上,分析低压台区线损构成与分类,如图3所示。
在此基础上,根据电网中的等值电阻将低压台区部分的电网从源端到尾端、从主干线到分支线划分为若干计算点[9],从而确定低压台区综合线损率,为低压台区节点抗损提供基础依据,过程为
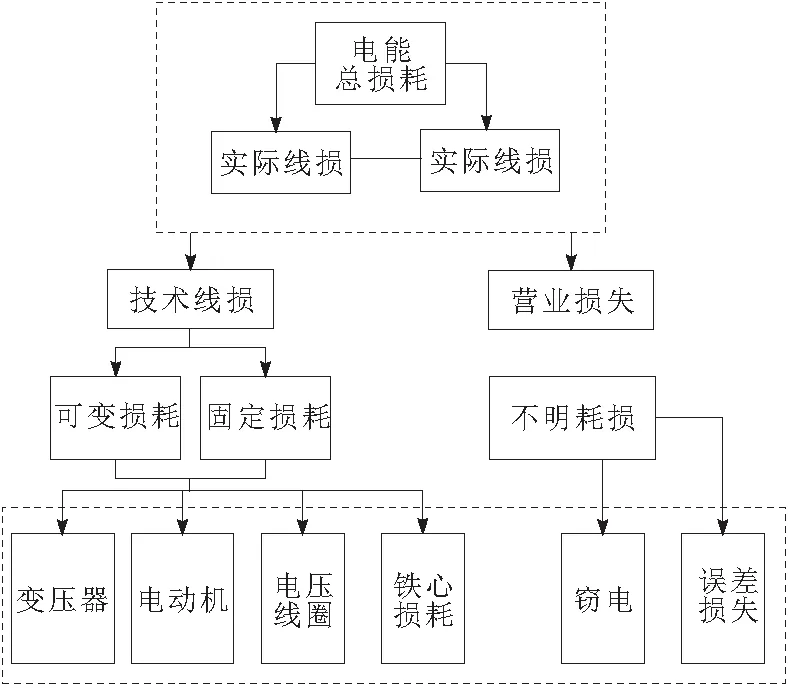
图3 低压台区线损构成与分类
(4)
e为实际抄表参数;y为某一供电阶段的抄表电量和;w为某一计算线段的结构常数。
3 低压台区节点抗损
依据上述过程构建低压台区节点抗损模型。低压台区线损管理部分模型框架如图4所示。

图4 低压台区管理部分架构
在此基础上,选择合适的导线截面[10-11]。计算导线电阻与导线截面积之间的关系,即
(5)
P为电网中导线的电阻率;Y为电网导线长度;s为导线截面积;t为电阻参数。
假设电网元件中电阻为Q,通过该元件的电流为I,当电流通过元件时产生的损耗为
(6)
一般情况下,电网中产生的损失通常在主干线上,需要合理调整运行电压[12-13]。因此,利用调相机等手段对电压调整,从而达到降损需求。电网电压与线损之间的关系为
(7)
V为台区配网额定电压;α为电压提高百分比。
根据上述计算,提高能够降低电网中的功率损失率[14]。在实际运行中,可适当的提高电压降低线损率,从而达到抗损目的,还能够增加输配电的能力。
为进一步提高低压台区节点的抗损能力,还需要对电网升级改造。目前,一些地区的电网相对落后,一些基本设施较为陈旧,在长期运行下,计量本身的损耗和计量本身计量误差都较大,因此需要根据实际情况实现抗损。同时,在同一台区,根据实际计算与往年数据统计分析,计算时按照统计后的值进行相应分配避免电流过大造成浪费。对于线损计算而言,电网在电能传输过程中也会造成有功损耗,并且会影响电能质量[15],所以在低压台区节点模型抗损中需对变压器进行无功补偿,减少电能传输过程中的损耗。
4 实验与分析
为检测基于分布式电源接入的低压台区节点抗损模型的应用性能,设计仿真实验加以验证。通过对比负荷、电压实测数据与实际数据,判断抗损模型的有效性。并以电压偏差为检验指标,对比本文模型、计及DG随机性的配网无功优化及抗损模型(传统模型1)、基于改进和声搜索算法的配电网抗损优化模型(传统模型2)的有效性。
4.1 实验准备
以某低压台区为实验对象,台区中设有2台变压器(容量均为1 500 MVA),其余的设备参数如表1所示。
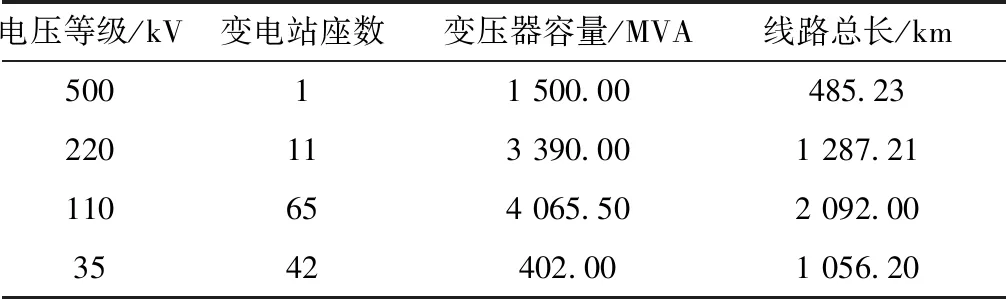
表1 实验台区输变电设备统计表
在MATLAB平台进行此次实验,其运行过程如图5所示。
根据变电站实际情况完成建模。实验采用RS485通信接口电能表获取数字电能表,并利用于GPRS通信实现实验数据的实时传输。在获取实验信息后,通过采集器对实验数据进行采集与管理,之后发送到管理系统中,并在仿真平台中完成对实际电量统计与计算。

图5 MATLAB运行过程
实验信息传输结构如图6所示。
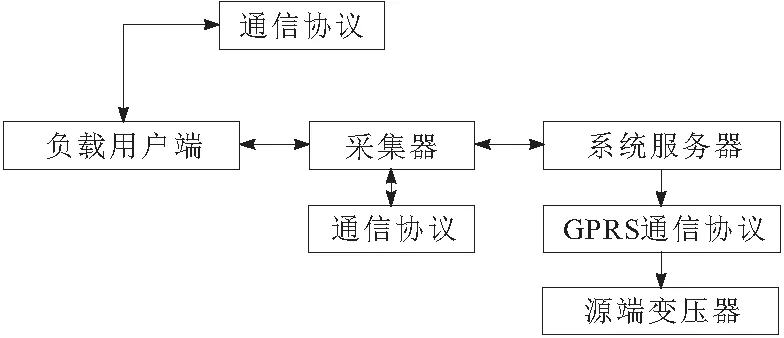
图6 实验信息传输结构
传输结构主要分为两部分,一部分是源端进入变压器的统计电量,另一部分为变压器负载用户的统计变量。源端数据直接通过GPRS通信,负载用户端采用采集器收集固定范围内的用户用电数据,然后将采集完成的数据传输至服务器,完成实验数据的采集。
4.2 实验结果与分析
选取110 kV、220 kV、500 kV 3条配电线路,分别编号为A、B、C,将线路尖峰负荷与电压值作为对比对象,分别使用不同抗损模型对上述2个内容进行计算,以该值判定模型计算的精准度。
3条线路的负荷与电压实际值如表2所示。
不同模型计算后的实验线路尖峰负荷与电压值如表3所示。

表3 实验结果对比
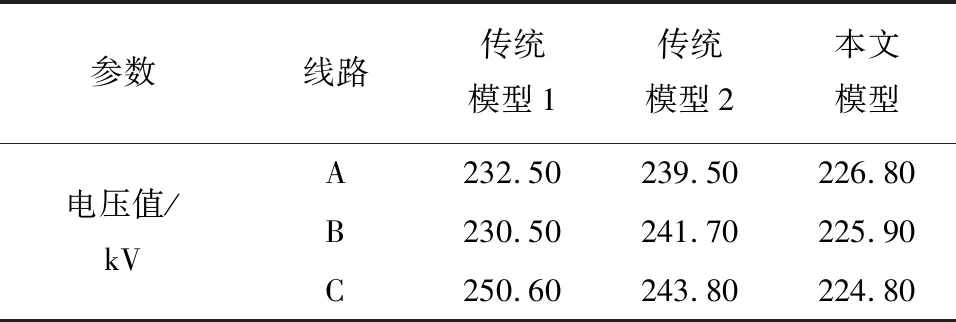
表3(续)
分析表3可知,将不同模型的计算得到的线路尖峰负荷值、电压值与实际的负荷值、电压值对比可知,2种传统模型的计算结果与实际值相差较大,而本文模型的计算机结果与实际的负荷值、电压值相差较小,在一定意义上可忽略不计。由此可以说明本文模型的计算精度较高,在此基础上,以电压偏差为验证指标,判断不同模型的抗损性能。电压偏差计算过程为
(8)
ΔU为电压偏差百分比;U为低压台区配网实际电压;Us为电网标称电压。
不同模型下的配网节点电压偏差对比如图7所示。
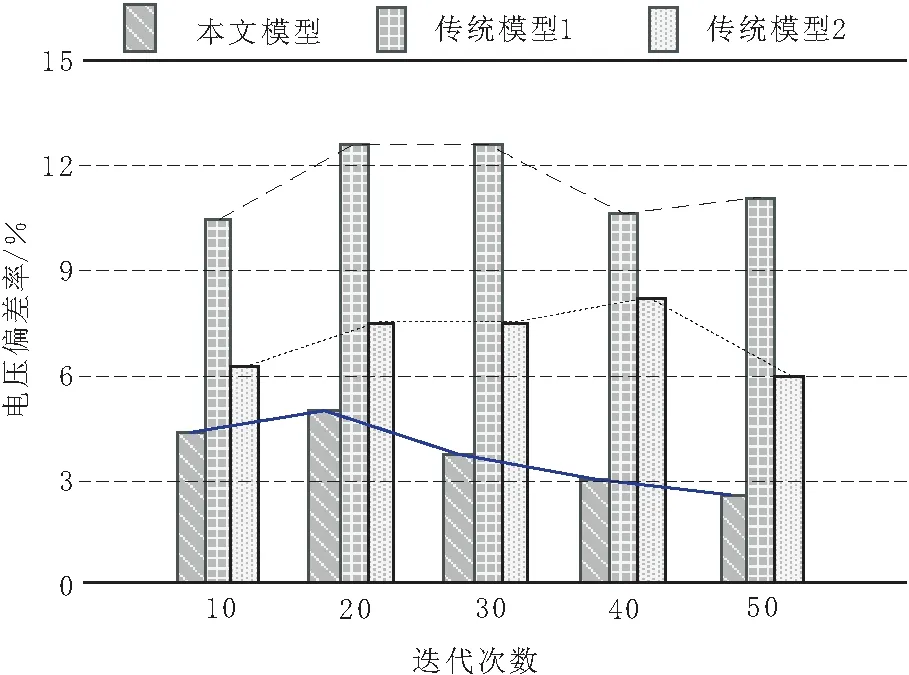
图7 不同模型电压偏差对比结果
分析图7可知,随着迭代次数的增加,不同模型下的电压偏差值也在不断发生变化。传统模型1的电压偏差始终保持在10.30%~12.50%之间,传统模型2的电压偏差始终保持在6.00%~8.10%之间,而本文模型的电压偏差始终保持在2.30%~4.80%之间。通过对比可知,本文模型下的低压台区配网节点电压偏差较小,说明本文模型的抗损性能好,具有一定的实际应用意义。
5 结束语
从影响配电网电量损耗的因素分析以及低压台区节点抗损的角度出发,基于分布式电源接入方式设计了一种低压台区节点抗损模型,并通过实验结果证明了该模型对负荷值、电压值的计算精准度较高,且该模型下的电压偏差较小,说明该模型能够保证供电可靠性,为智能电网的发展提供支持。但是此次研究的方法还存在一定的不足,在低压台区节点负荷预测中还存在欠缺部分,在后续研究中将充分分析节点负荷,完善方法的动态分析能力,从而进一步提高负荷值、电压值的计算精准度,为电网运行提供帮助。
