基于TDR的多孔介质中含水/水合物饱和度测量方法仿真研究

王亚军，贺世超，邢兰昌，魏 伟，韩维峰，齐淑英

(1.中国石油大学 (华东) 控制科学与工程学院，山东 青岛 266580;(2.中国石油勘探开发研究院 新能源研究所，河北 廊坊 065007)

0 引言

天然气水合物是由天然气与水在高压低温条件下形成的类冰状的结晶物质，自然界中的水合物主要分布于深海沉积物或陆地永久冻土中[1]，原位测量十分困难，因此通过室内模拟实验模拟储层中天然气水合物的生成/分解过程探究其物性响应规律，是准确评价实际储层水合物资源量的重要手段。含水合物沉积物样品中含水/水合物饱和度的实时在线监测是水合物模拟实验中的重要环节。目前模拟实验中测量含水/水合物饱和度的方法主要有直接测试估算法[2]、压差法[3]、时域反射法(Time Domain Reflectometry,TDR)[4]等。

直接测试估算法通过测量样品中水合物分解释放的气体体积来计算水合物的量进而求得含水合物饱和度，但实验中释放出的气体有可能来自未完全反应所剩余的游离气，从而导致测量结果偏大；压差法根据反应前后容器内气体压力的变化计算甲烷气体消耗量及含水合物饱和度，但此方法需将气体看作理想气体，测量结果同样存在偏差。通过上述两类方法得到的含水合物饱和度是对反应体系的整体描述，并不能对反应体系的局部进行测量。TDR技术通过测量样品的表观介电常数来监测含水合物饱和度的变化，介电常数几乎不受样品孔隙水盐离子浓度及温度、压力的影响[5]，而且通过设计TDR探针的结构能够测量样品局部的含水合物饱和度值，因此在含水合物饱和度测量方面具有独特的优势。

TDR技术最初用于查找通讯电缆的受损点，Topp等[6]提出将TDR用于土壤含水量的监测，得到了估算土壤中含水量的经验关系式；Wright等[7]将TDR应用于室内水合物模拟实验中，建立了含水合物沉积物的介电常数与含水量之间的关系式。针对电磁波衰减严重的高电导率测试环境，胡高伟等[8]应用聚烯烃材质热收缩套管对TDR探针进行了改进，并建立了不同盐度下沉积物介电常数与含水量的经验关系式；Chen等[9]基于时域分析提出了表面反射系数法，但未将其应用于沉积物的测量。近年来陈仁朋等[10]基于频率步进原理开发了新型的TDR系统并应用于测量土体含水率。

含水合物/水沉积物的各向异性、变化的孔隙水盐度、黏土等储层因素影响沉积物的介电常数和电导率，从而对TDR响应特性产生复杂的影响，并且对TDR探针的结构参数提出了特殊的要求。为了将来优化设计TDR探针结构，建立可靠的含水/水合物测量模型，本文利用有限元数值模拟方法建立了TDR测量过程数值仿真模型，基于该模型分析了电磁波穿过具有不同电导率、介电常数被测介质时的波形变化特性，讨论了不同被测介质参数对反射波形的影响规律。

1 TDR工作原理及仿真模型建立

1.1 TDR工作原理

TDR探测仪主要包括发射机、接收机、发射接收系统、电缆、TDR探头、信号处理器和显示器，各部分之间的连接关系如图1所示。图2为三针式TDR探头及仿真模型结构。TDR探测仪采用形成时间法，其工作过程为[11-12]：TDR发射机发射一个电压脉冲，其以电磁波的形式经同轴电缆传输至TDR探针起始端；电磁波从起始端进入探针和被测介质，传播到探针末端后发生反射，经探针和被测介质后返回到探针起始端；反射波被接收机所接收，经信号处理器处理后由显示器进行波形显示。

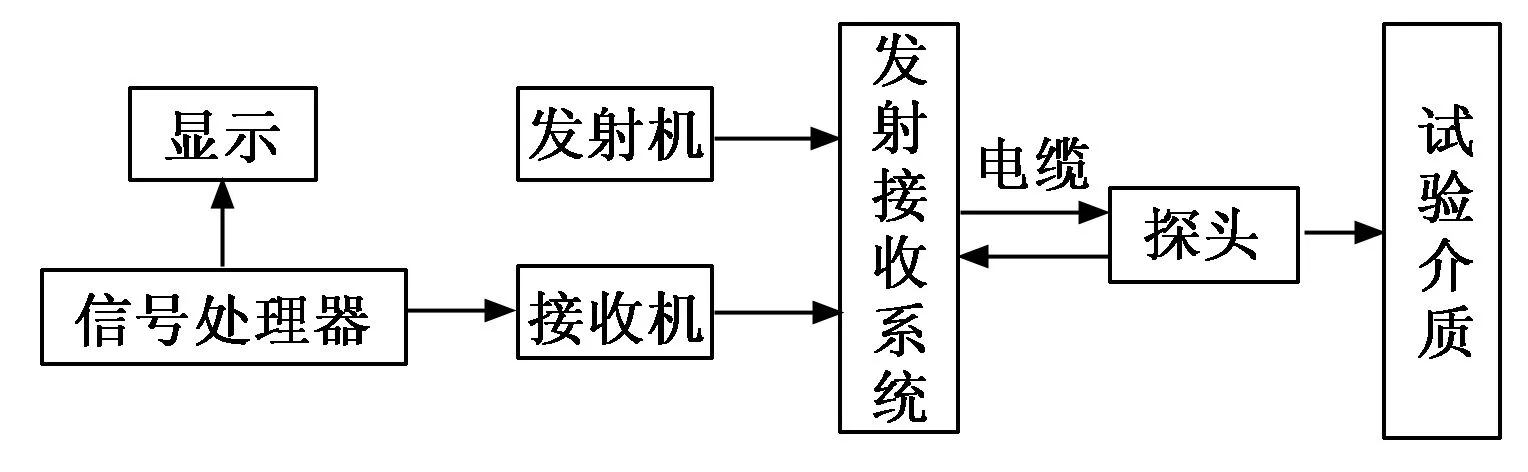
图1 TDR探测仪基本组成

图2 三针式TDR探头及仿真模型结构

参照图2，电磁波从探针起始端传播到末端并返回到起始端的总时间为Δt，由Δt和探针长度L可计算出被测介质的相对介电常数εr[13]：

εr=(CΔt/2L)2

(1)

式中，C为真空中电磁波的传播速度。

对于含有水和水合物的沉积物，其体积含水量可以由Wright等提出的经验关系式来计算：

θV= -11.967 7 + 4.506 072 56εr-

0.146 15εr2+ 0.002 139 9εr3

(2)

式中，θV为沉积物的体积含水量。通过测量得到样品的初始孔隙度Φ，进而可得出含水合物饱和度Sh为：

Sh=(Φ-θV)/Φ×100%

(3)

1.2 数值仿真模型的建立

1.2.1 几何结构与网格

根据电磁波在波导中的传播规律，TDR探头的中间探针可模拟为同轴电缆的内导体，外部探针模拟为同轴电缆的外导体，探针间的试验介质则充当同轴电缆的填充介质[14]。本研究选取探针起始端与末端之间的部分进行建模，考虑到所研究部分的几何结构具有轴对称特性，因此建立二维模型。参照图2，探针长度L为15 cm、探针直径为2 mm，相邻探针间距为2 cm。

模型网格划分越精细，计算结果的准确度越高，但是所需的计算时间越长。为保证模拟结果的准确性并考虑计算速度和计算量，该模型采用最大单元尺寸为5×10-5m的三角形网格。

1.2.2 模型参数设置

1)发射信号:选取调制高斯脉冲信号为TDR发射机输出的发射信号，其时域表达式为式(4)，脉冲频率f为100 MHz，脉冲幅值为1 V，脉冲宽度为40 ns。

V0=S(t)sin(2πft)

(4)

式中，V0为输入TDR探针的信号，S(t)为调制前的高斯脉冲，f为正弦波频率。

2)材料特性参数:根据被测介质的不同性质设计了3组仿真实验，即空气、浓度不同的氯化钠溶液和水合物含量不同的石英砂。通过设定材料的特性参数来模拟上述3种被测介质，主要材料参数包括：相对介电常数、电导率和相对磁导率，其中相对磁导率值均设为1。

模拟空气时，相对介电常数为1、电导率为0 mS/m；模拟浓度不同的氯化钠溶液时，相对介电常数为81，电导率变化范围为0～500 mS/m；模拟水合物含量不同的石英砂时，相对介电常数的范围为12～18(参照式(2))、电导率为0 mS/m。

3)边界条件和求解模型:在TDR探针的末端，即被测介质底部(参见图2)设置3种不同的边界条件来模拟负载情况，即：理想导体(PEC)、完美磁性导体(PMC)和集总端口(波激励为关闭状态)，分别用来模拟电磁波传播过程中的短路、开路和阻抗完全匹配的情况。

根据同轴线的传输理论，定义电磁波沿探针传播方向为z，电磁波在其中以TEM波的形式传播，则仿真中求解电场参数的解析式如下[15]：

V=V+e-γz+V-eγz

(5)

其中：V为内外电极之间的电压；z代表传输线中的位置；V+、V-是一般解的未知常数，可通过边界条件确定；γ为传输线的传播常数。

在数值仿真模型求解过程中，实时获取了TDR探针起始端的信号波形数据，通过分析入射脉冲信号与反射信号的波形特征来讨论被测介质特性参数与反射波之间的关系。

2 模型应用与结果分析

2.1 仿真模型的检验

首先模拟被测介质为空气(介电常数为1，电导率为0)的情况，通过分析模型求解结果来验证仿真模型的正确性。图3所示为分别对TDR探针末端边界设置为短路、开路和阻抗完全匹配等3种情况时在探针起始端采集到的信号波形。

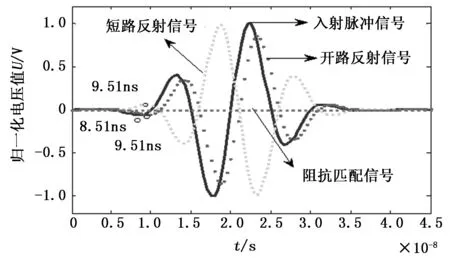
图3 被测介质为空气时所获取信号的波形

分析图3可见：当负载阻抗为0(短路)时，反射信号幅值等于入射脉冲信号幅值，两者极性相反；当负载阻抗为∞时(开路)，反射信号幅值等于入射脉冲幅值，两者极性相同；负载阻抗匹配时，无反射信号产生。

选取图3所示入射脉冲信号的第一个波谷点作为信号起始位置，反射信号的第一个波峰(谷)点作为反射起始点。负载为开路时，两点之间的时间差为约1.03 ns，已知TDR探针长度为15 cm，计算得到电磁波传播速度为2.91×108m/s；负载为短路时，两点之间的时间差约为1.001 ns，传播速度为2.99×108m/s。电磁波在真空中传播速度速为2.997 9×108m/s，仿真结果的误差处于3%以内。

上述结果表明仿真计算与理论分析一致，从而验证了所建立仿真模型的正确性。

2.2 以不同浓度氯化钠溶液为被测介质

通过调节电导率值来模拟氯化钠溶液浓度的变化，电导率的变化范围是0～500 mS/m，图4所示为电导率分别为0 mS/m、100 mS/m和350 mS/m时的信号波形。由图可见，电导率为0 mS/m时，介质对电磁波信号无抑制作用，反射信号幅值等于入射信号幅值。当电导率不为0时，反射信号的幅值出现衰减，电导率越大衰减越严重。当σ=350 mS/m时，反射信号幅值衰减为原来的1%。

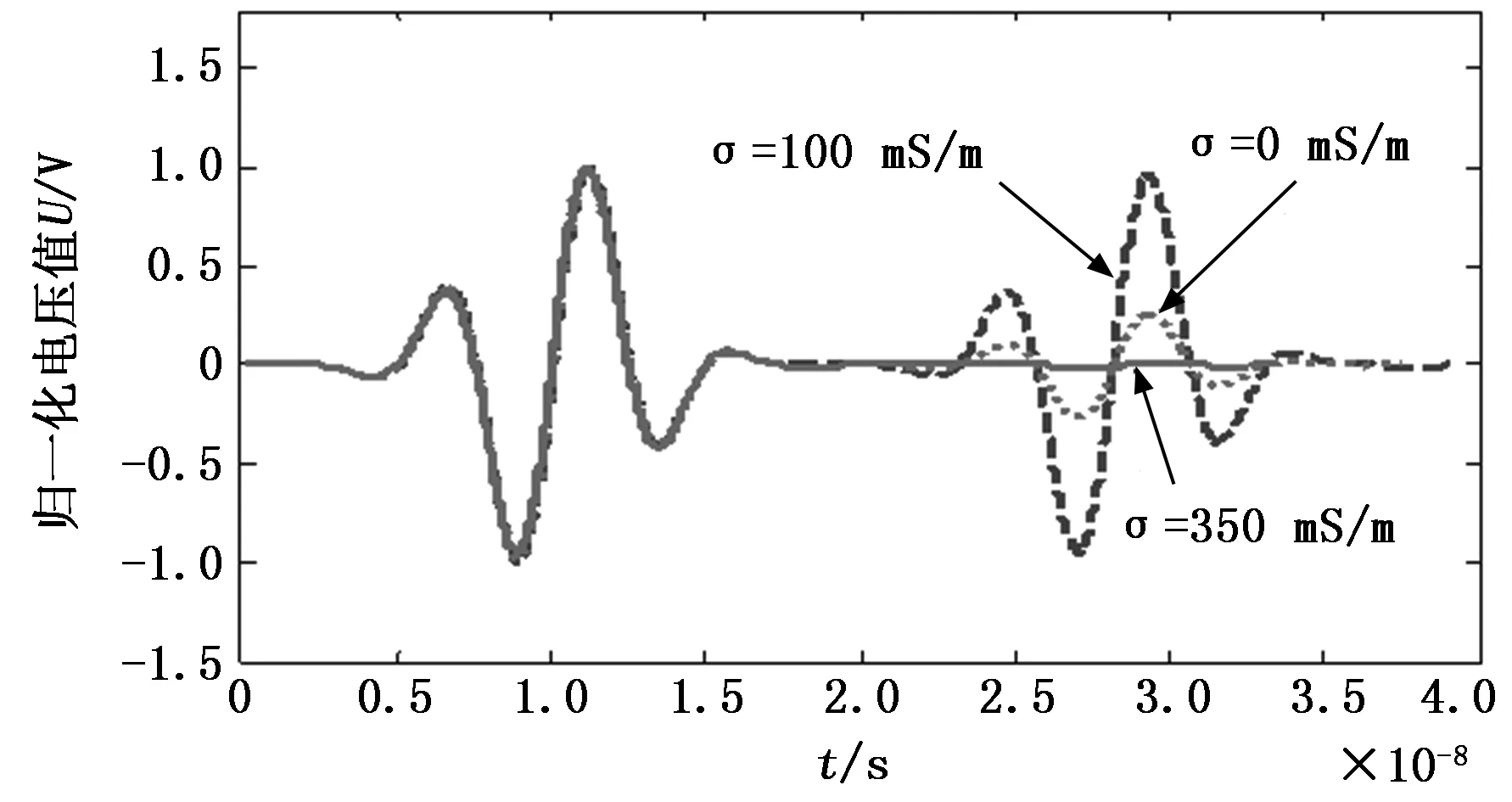
图4 不同浓度的氯化钠溶液为被测介质时的波形

电磁波在均匀有耗导电媒质中传播，当频率f满足式(6)时，媒质中位移电流占主导地位，传导电流影响很小，可以忽略不计[17]。此时，反射信号衰减系数与介质介电常数、电导率之间的关系可表示为式(7)。由式(7)可知，当被测介质为不同浓度的氯化钠溶液时，假定介电常数不变，则衰减系数只与电导率有关[18]。

(6)

(7)

沿着插入介质中的TDR探针传播的电磁波信号，其电压幅值按照式(8)所表示的规律衰减。

(8)

式中，VR是探头末端反射信号的电压幅值；VT是入射脉冲信号的电压幅值；α为衰减系数；L为探针长度的2倍(数值模型中信号获取点为探针起始点)。

用1-VR/VT来表示电磁波沿探针传播过程中的衰减幅度。依据仿真结果与式(7)和式(8)，得到反射信号衰减幅度随电导率变化的曲线，如图5所示。当电导率小于290 mS/m时，反射信号幅值随电导率的增加而衰减的较快，当电导率为290 mS/m时衰减幅度达到90%；当电导率大于290 mS/m时，反射信号幅值衰减变缓，当电导率为500 mS/m，电磁波信号能量衰减到0。由图可知，反射信号衰减幅度的仿真曲线与理论曲线几乎重合，二者所反映的规律一致，验证了仿真模型的准确性。

图5 反射信号衰减幅度随电导率变化的曲线

2.3 以不同水合物含量的石英砂为被测介质

当被测介质为水合物含量不同的石英砂时，保持电导率和相对磁导率不变(σ=0，μ=1)，依据现有模拟实验数据中样品的饱和度变化范围，分别取含水合物饱和度在0%～40%变化范围内相应的相对介电常数值进行研究[18]。假定样品孔隙度为40%，此时体积含水量为40%～24%，由式(2)计算得到表观介电常数的变化范围为23～12。

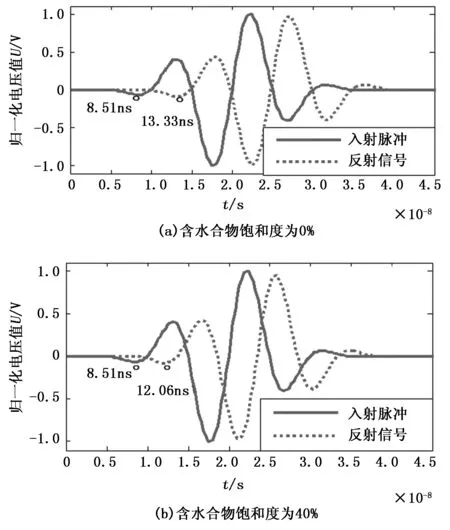
图6 不同水合物含量石英砂的相对介电常数对电磁波传播速度的影响

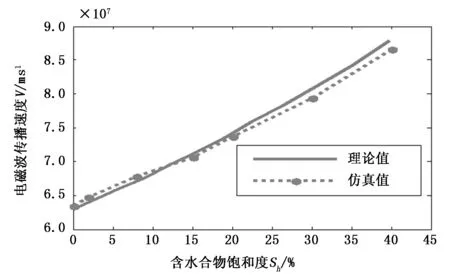
图7 电磁波传播速度随含水合物饱和度变化的曲线

3 讨论

在目前所进行的仿真工作中，设定材料参数为固定值，即被测介质的材料具有理想的均一性。而在含水合物沉积物模拟实验的实际应用中，水合物在多孔介质中的分布并不均匀，这将会对TDR测量波形造成干扰，如产生反射杂波、测量误差增大等。因此，在下一步仿真工作中，可将被测区域填充各向异性材料，这对于研究TDR在实际环境下的测量特性具有重要指导意义。

4 结束语

利用有限元数值模拟方法建立了TDR测量过程数值仿真模型，分别以空气、不同浓度氯化钠溶液以及不同水合物含量的石英砂为被测介质验证了模型的正确性、研究了被测介质电导率和介电常数对反射波形的影响规律。

通过改变被测介质的介电常数来模拟含水/水合物饱和度不同的石英砂，随着石英砂中水合物含量的增加，含水量逐渐降低，表观介电常数随之减小，电磁波传播速度随之以非线性形式增加；与理论值相比较，仿真计算所得到的传播速度最大误差处于5%以内。

建立TDR测量过程数值仿真模型为优化设计TDR探针结构，建立基于TDR响应的含水/水合物测量模型提供了研究工具。下一步需要在被测区域中填充各向异性材料，更加真实地模拟含水合物沉积物被测介质。