基于匹配理论的电力物联网边缘服务器选择机制
2020-09-02王一然
王一然
(华北电力大学,北京 102200)
泛在电力物联网就是围绕电力系统各环节,充分应用现代信息技术,实现电力系统各环节的智能化。随着泛在电力物联网的建设,上传数据量爆炸式增加,集中式的处理不再能够满足需求[1]。移动边缘计算(Mobile Edge Computing,MEC)被认为是解决此问题的有效方式,它将具有空闲资源的MEC服务器等各种设施当作分布式边缘,将计算任务加载到物理上靠近数据源的移动边缘,以显著减少传输延迟[2]。
1 介绍
文章考虑移动设备和MEC服务器的计算能力、无线信道条件和时延约束,将MEC系统中的任务分配问题归结为一对一的匹配问题。该任务分配机制的主要目标是在满足设备延迟需求以及良好可扩展性的同时,降低总体能耗[3]。
文章主要进行了以下研究:(1)MEC系统中的任务分配问题。提出了分布式执行的任务分配机制[4]。(2)理论上证明了该任务分配机制能够使设备和MEC服务器之间保持最稳定的匹配。(3)该任务分配机制可以显著降低总体能耗,并能够良好地平衡计算的复杂性和能耗。
2 系统模型
文章假设所有移动设备都能生成任务,但仅具有过多计算能力的设备和MEC服务器[以下统称为边缘节点(Edge Nodes,ENs)]才能进行计算任务。文章假设大多数任务可以在一个时隙内完成,而大型任务被分成若干子任务,子任务可以在一个时隙内完成。下文中的“任务(Tasks,Ts)”将用于指在一个时隙中作为一个整体计算的任务[5]。
文章模拟了一个MEC场景。该场景中有M个Ts,Ts集为T={T1,……,Tm},有N个ENs,ENs集为E={E1,……,Em}。ENs可以将资源平均划分为多个虚拟资源单元(Virtual Resource Units,VRU),从而实现任务的并行计算。Ej处的VRU数量称为Ej的配额,用Qj表示。假设VRU在不同ENs下的计算能力不同,用CPU频率(Hz)来描述ENs的计算能力,即Ej处的每个VRU的CPU频率用Fj表示。
3 问题描述
匹配理论是描述随着时间的推移形成互惠关系的数学框架。匹配时,双方会形成对彼此的偏好列表。因此,基于匹配理论的协议一般无需集中式协调器,且具有良好的可扩展性。文章将MEC系统中的任务分配问题转化为匹配博弈。Ts和ENs是要互相匹配的不相连代理集。假设一个Ts只能分配给一个ENs,一个ENs只能接受一个Ts。Sij表示Ti与Ej是否匹配。Sij=1表示匹配,而Sij=0表示不匹配。

3.1 时延问题
时延是任务分配中需要解决的主要问题,不同的设备对时间的敏感度不同。延迟容限定义为从计算请求发出到任务完成的时间,表示设备的时间敏感性。Ti的延迟容限用表示。加载Ts会产生额外的传输能耗和传输延迟,因此每个Ts必须仔细决定任务加载到哪个相邻的ENs。总体延迟通常由3个部分组成:(1)传输延迟。(2)排队延迟。(3)计算延迟。
传输延迟是指通过无线连接将Ts传输到ENs的时间。队列延迟是任务在队列中等待直到可以执行的时间。文章假设每个Ts均使用EN或VRU的全部资源执行Ts(即可以省略排队延迟)。计算延迟取决于EN的计算能力,是执行Ts所需的时间。Ti与Ej匹配时的总延迟Lij表示如下:

其中,Ci表示成功执行Ti所需的CPU周期数。
文章假设Ts使用正交信道进行输入数据传输(即用户间干扰可以忽略)。每个设备传输数据是独立的,不受其他设备及ENs的干扰。则传输延迟如下:

其中,Mi表示Ti的输入数据大小;γij(t)是Ti在第t个时隙中到Ej的信道功率增益;是传输功率;B是系统带宽;N0是接收器处的噪声功率谱密度。
3.2 效用函数和优化问题
在匹配算法中,效用函数用于衡量Ts或ENs从任务分配中获得的净收益。根据Ej计算的Ti的效用定义如下:

其中,ri是Ti的满意度,即Ti在指定的延迟容限内的完成度;a是能源成本系数;λ表示ENs计算Ti时,Ti为每个CPU周期支付的单价。(总付款λCi与任务的大小Ci成比例)。
Ej完成Ti获得的效用如下:

资源有限的设备在考虑设备和MEC服务器的计算能力、无线信道条件和延迟限制的同时,将Ts加载到附近的ENs。此时,问题被转化为效用最大化问题,任务分配受延迟的约束。所有Ts和ENs在Sij上的总效用如下:
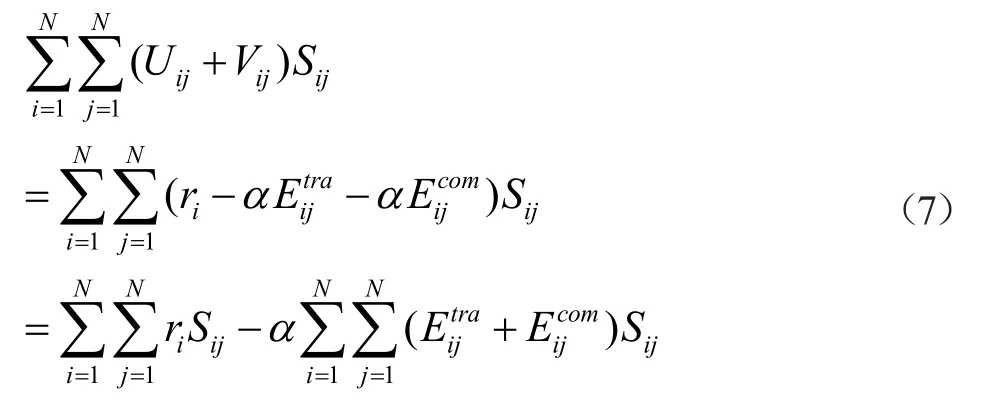
整体效用最大化问题即整体能耗最小化问题:

延迟约束能耗优化问题定义如下:(1)保证每个Ts只分配给一个EN;(2)保证每个Ts按时完成;(3)保证每个Ts和EN的效用为正;(4)信噪比应高于阈值,以保证成功传输(可靠传输约束)。
4 基于匹配理论的解决方法及性能分析
文章的任务分配算法是分布式的问题优化算法,该算法由初始化阶段和多次迭代组成。
4.1 初始化部分
为所有任务建立偏好列表。偏好是根据本地信息进行评估的,本地信息被定义为一个效用函数,表示通过特定任务匹配所获得的收益。效用函数如下:

公式(10)表示能够将Ti的输入数据传输到的ENs的一组可靠连接。

4.2 迭代部分
文章定义已匹配的任务集为Mmatch,未匹配的任务集为Munmatch。属于Munmatch的Ti向在其偏好列表中排名第一的Ej发送请求且Ti宣布其计算要求。如果Ej未匹配并且满足Ti的计算要求,则接受Ti的匹配请求,并将Ti从Munmatch中删除,添加到Mmatch中。否则,Ti的请求将被拒绝。
如果Ek已与Ti匹配,但Ej能更好地满足Ti的计算要求,则接受Ej,并将Ek从Mmatch中移除,添加到Munmatch,将Ej从Munmatch中移除,添加到Mmatch。否则,Ej的请求将被拒绝。
如果Ti不与任何ENs匹配,表示没有ENs能够满足Ti的计算要求,则将Ti从Munmatch中删除,直至Munmatch为空集。
4.3 稳定性分析
匹配的关键在于结果是否稳定。在任务分配系统中,匹配的稳定性偏差是固定的,这使得任何一个匹配对都不会偏好先前的匹配结果。
引理:当算法结束时,任务和边缘节点的匹配是稳定的。
证明:如果Ti和Ej都完成匹配(但并非Ti和Ej进行了匹配)。算法完成后,Ti和Ej不能继续匹配,如果Ti偏好Ej而非当前匹配对象Ek,则Ti必定在与Ek完成匹配之前向Ej发出过匹配请求。如果Ej接受其匹配请求,但在算法结束时并未与Ti配对,则说明Ti因Ek更好而放弃与Ej匹配。
5 结语
文章提出了基于匹配理论的MEC系统任务分配机制,该任务分配机制是优化驱动的,可以分布式执行。文章在考虑到移动设备和MEC服务器的计算能力、无线信道条件和延迟约束的条件下,以最小化能耗为目标,建立了任务分配问题,并提出了一种基于一对一匹配的算法,从理论上证明了该任务分配机制能够使设备和MEC服务器之间保持稳定的匹配,并且良好地平衡了计算复杂性和能耗。
