基于粒子群算法的分布式电源优化配置研究
2020-09-01杨更宇
杨更宇
(华北电力大学电气与电子工程学院,北京 102206)
0 引言
当前,随着互联网和信息技术的发展,产生了“能源互联网”这一概念。局域能源互联网是一个局部能量系统,在其内部各种形式的能源和区域负荷相满足。局域能源互联网中包含了各种类型的分布式电源,如风力发电机、光伏发电系统、燃气轮机等,利用分布式电源就能满足终端的负荷需求,具有减少输电损耗、减轻环境污染、供电可靠性高的优点。当前,能源互联网的研究刚刚起步,其规划设计和运行控制都还有待深入研究。分布式电源的优化配置是局域能源互联网规划设计中的一个重要环节,这是保证其可靠、经济运行的关键。
目前,国内外学者对微网中的电源优化配置问题进行了相应的研究。文献[1]考虑了需求侧响应,建立了以总成本最小为优化目标的产业园区供电系统分布式电源/储能系统优化配置模型,并利用组合型智能算法求解该问题;文献[2]针对典型混合能源微网系统,以年现金流最小为优化目标,采用变步长空间搜索方法计算最佳分布式电源容量;文献[3]针对并网运行的微电网,以计及设备投资及运行成本、电能交易成本为主的系统等年值成本最小为优化目标函数,并采用自适应权重粒子群算法进行求解。文献[4]分别建立了配电网和分布式电源双层优化模型,上层规划配电网的网架结构和联络线方案,下层规划DG的位置和容量,并采用改进的粒子群—模拟退火算法求解该问题。
本文以局域能源互联网为研究对象,首先介绍了局域能源互联网的基本概念及组成。在此基础上,介绍了分布式电源的出力模型。然后,建立分布式电源优化配置的数学模型,并采用粒子群算法对其进行求解。最后,结合实际算例进行了仿真计算,给出了分布式电源的配置方案,并详细分析了粒子群算法参数变化对配置结果及算法性能的影响。
1 局域能源互联网的概念
局域能源互联网是一个利用分布式电源产生电、热、冷、气等多种形式的终端能量、区域内用户就地利用、储能装置参与调配的综合能源系统。它是一个自成系统的完整的底层单元,是自治运行的能量系统[5],所供给的是一个局部用能单位,如工业园区、大学校园、商业区、居民社区等。
从物理结构层面上,通常将局域能源互联网分为源、网、荷、储4部分。
1)源:即能源供应侧,如风电、光伏、燃气轮机、溴化锂制冷机等。
2)网:分为能源耦合网络和信息互联网络。能源耦合网络即冷、热、电各种能量的传输网络,信息互联网络即采用各种传感检测装置,实时采集能源供应侧、能源网络、用户侧的信息,并传递给能量管理设备(如能量路由器等)的网络。通过信息互联,区域能源供应商和用户能够进行互动,用户可以进行需求侧响应,能源供应商可以进行动态调度,二者共同实现利益最大化。
3)荷:即该互联网内部的负荷,它包括电力负荷、热负荷、冷负荷等。冷、热、电的负荷预测对于局域能源互联网的规划、运行有着重要的意义。
4)储:即储能系统,包括电储能、热储能和冷储能,通常指的是电储能。储能系统可以有效平抑分布式电源的功率波动,并可以在出现功率缺额时进行弥补。同时,在并网运行模式下,利用峰谷时段的电价差,储能系统可以在用电高峰放电,用电低谷充电,起到盈利的作用。

图1 局域能源互联网示意图
2 分布式电源出力模型
2.1 风机出力模型
风电机组输出功率PWT与风速v之间可以近似用以下分段函数表示[6]:
(1)
式中,vci为切入风速,vr为额定风速,vco为切出风速,Pr为风机额定功率。A、B、C为功率曲线的参数,可由下列公式得出:
(2)
(3)
(4)
2.2 光伏阵列出力模型
光伏阵列实际输出功率可由标准条件下的输出功率、光照强度、环境温度计算得到[7]:
(5)
式中,PPV表示工作点的输出功率;STC特指太阳辐照度GSTC为1 kW/m2,电池表面温度TSTC为25℃,相对大气光学质量为AM1.5的条件;Gc为工作点的辐照度;k为功率温度系数;PSTC为标准条件下光伏阵列的额定输出功率;Tc为工作点的电池表面温度,它通常是环境温度Ta与风速的函数:
Tc=Ta+αGc
(6)
其中系数α为风速v的指数函数:
α=f(v)=c1+c2ec3v
(7)
式中c1、c2、c3为常系数。
2.3 燃机出力模型
本文考虑燃气轮机—烟气型吸收式冷热电联产系统,其示意图如图2所示[8]。

图2 燃气轮机—烟气型吸收式冷热电联产系统
该系统的基本工作原理为:首先使用天然气进入燃气轮机做功,驱动发电机发电,然后由烟气型溴化锂吸收装置回收利用烟气中的余热,溴化锂机组可以同时提供冷、热负荷,或在不同时段分别提供这两种负荷以满足用户需要[9]。该系统适用于没有蒸汽热负荷需求,仅有冬季采暖、制冷及生活热水负荷的用户。
基于冷热电联产的燃气轮机数学模型可表示为:
(8)
QHE(t)=QGT(t)KHE
(9)
QCO(t)=QGT(t)KCO
(10)
(11)
式中,QGT(t)为t时刻燃气轮机排出的烟气中的余热量;PGT(t)为t时刻燃气轮机发出的电功率;ηe为燃气轮机的发电效率;ηl为燃气轮机的热量损失率;QHE(t)表示t时刻溴化锂吸收式制冷机的制热量;KHE为制冷机的制热系数;QCO(t)表示t时刻溴化锂吸收式制冷机的制冷量;KCO为制冷机的制冷系数;VGT(t)为t时刻燃气轮机消耗的天然气量;LNG为天然气的低位热值,取9.78(kW·h)/m3;Δt为时间步长,取1 h。
3 分布式电源优化配置数学模型
3.1 优化目标函数
以局域能源互联网系统年均成本最小为目标函数,如下式所示:
minC=CDG+CGT+CGrid
(12)
式中,C表示局域能源互联网系统年均成本;CDG、CGT、CGrid分别表示风光、燃机系统的年成本以及系统的年购电成本。
各项费用的具体表达式如下[10-12]:
1)风光的年成本。
(13)
式中各参数的含义见文献[13]。
2)燃机系统的年成本。
CGT=Cinv+Cgas
(14)
Cinv=(Ntur·Ctur+Ntur·Cass+Creg+Cspp)
(15)
(16)
式中各参数的含义见文献[13]。
3)年购电成本。
(17)
Pgrid(t)=PLoad(t)-PWT(t)-PPV(t)-PGT(t)
(18)
式中各参数的含义见文献[13]。
3.2 约束条件
1)设备出力应满足其出力上限约束[13],即:
(19)

2)能量平衡约束[13-14]。
式中各参数的含义见文献[13]。
3)电源占地面积约束。
Ni≤Ni,max
(23)
式中,Ni,max表示受当地面积限制,第i种电源所能安装的最大数量。
4)联络线路功率约束。局域能源互联网和大电网之间交换的功率值应在联络线路功率限制的范围内:
|Pgrid(t)|≤Pline,max
(24)
式中,Pline,max表示局域能源互联网与大电网间联络线路功率限制。
3.3 求解算法
本文的分布式电源优化配置模型为一个含约束条件的线性规划问题,考虑采用粒子群算法进行求解[15-16]。粒子群算法初始化为一群随机粒子(即随机解),然后通过不断迭代找到最优解。在每一次迭代中,粒子通过跟踪个体极值与全局极值来更新自己。在找到这两个最优值时,每个粒子根据如下的公式来更新自己的速度和位置:
(25)
(26)
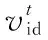
约束条件的处理:约束条件1)在本文的算例前提条件中已经保证,约束条件2)中的冷、热平衡约束已在燃机供热方案制定过程中得到满足,约束条件3)将处理为优化变量的上限。因此,将等式约束条件2)中的电功率平衡约束中的自变量Pgrid(t)表示成其他自变量的形式,不等式约束4)转化为罚函数加在目标函数上构成适应度函数,如下式所示:
(27)
g=|PLoad(t)-[PWT(t)+PPV(t)+PGT(t)]|-Pline,max
(28)
其中,φ为适应度函数,C为本文目标函数,W为惩罚因子。
基于粒子群算法对分布式电源优化配置模型的具体求解流程如下。
1)步骤1:根据热负荷和以热定电原则,初步确定几种预选的燃机供热方案,并给出每种预选方案下的燃机电出力。
2)步骤2:根据气象参数和设备参数,计算单台风机、单片光伏组件的出力。
3)步骤3:在每一种燃机方案下,采用粒子群算法,将风机、光伏的数量N作为优化变量,适应度函数为φ。
4)步骤4:随机生成M组风光数量N作为初始群体,初始化风光数量N的值x。
5)步骤5:根据群体中每一组风光数量的值x,将x代入φ计算每一组风光数量N的适应度值。
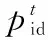
7)步骤7:根据公式(25)(26),更新风光数量N的迭代量v和值x。
8)步骤8:转到步骤5,若达到最大迭代次数则停止迭代。
9)步骤9:输出全局极值及其对应的目标函数值。
10)步骤10:比较所有方案下的全局极值对应的目标函数值,取其中的最小值作为局域能源互联网最优系统年均成本,并输出此时的燃机型号、容量、风光的数量。
4 算例分析
4.1 分布式电源优化配置
以某工业园区为研究对象,对该工业园区分布式电源容量进行优化配置。考虑并网运行,联络线功率限制为15 MW,风光数量受其安装上限限制,风机上限4台,光伏上限6 500片。燃机系统考虑采取“以热定电”的配置原则。优化的变量包括风光的数量、燃机的型号及容量。粒子群算法的初始参数设置为:种群规模M取100,最大迭代次数gmax取100,学习因子c1=c2=1.5,惯性权重系数ω取0.8,最大速度vmax=[1 200],最小速度vmin=[-1 -200],最大位置xmax=[4 6 500],最小位置xmax=[0 0]。惩罚因子W取106。
计算结果如表1所示。
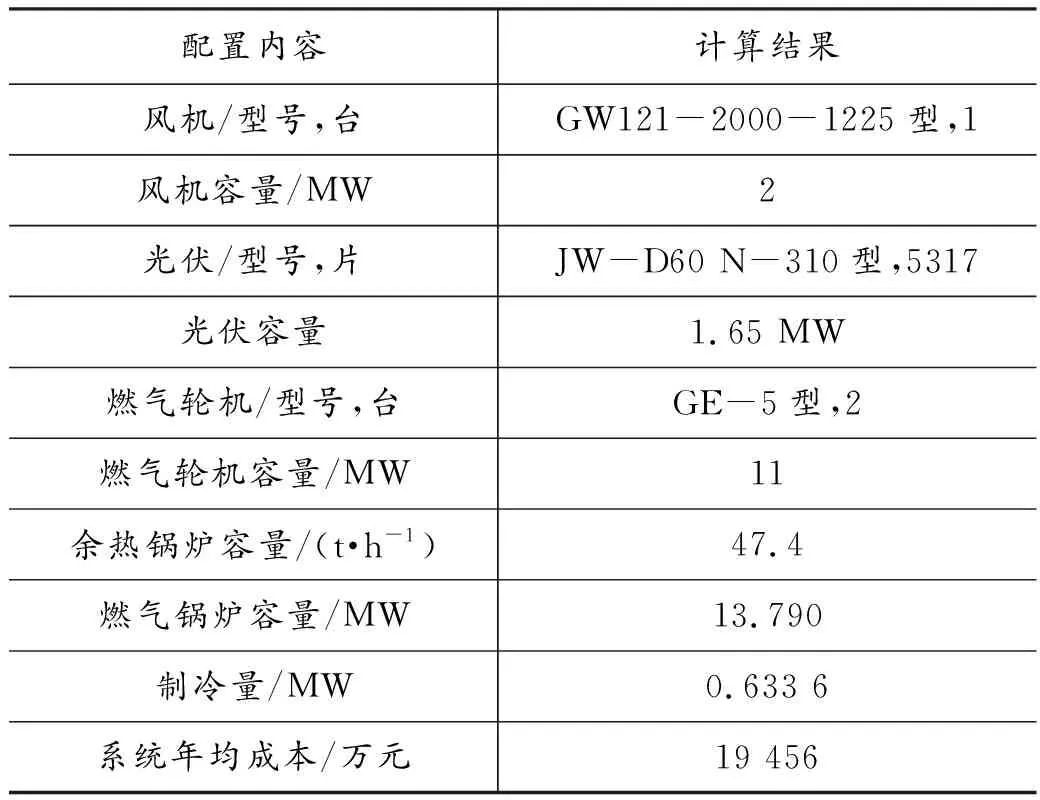
表1 优化配置结果
配置的数量均取整数。燃机为满足热负荷的需求配置为2台,额定容量为11 MW。风机配置1台,总容量为2 MW。光伏配置5 317片,总容量为1.65 MW。优化出的系统年均成本为19 456万元。
适应度函数随迭代次数的变化曲线如图3所示,可以明显地看出从第16代时开始收敛。
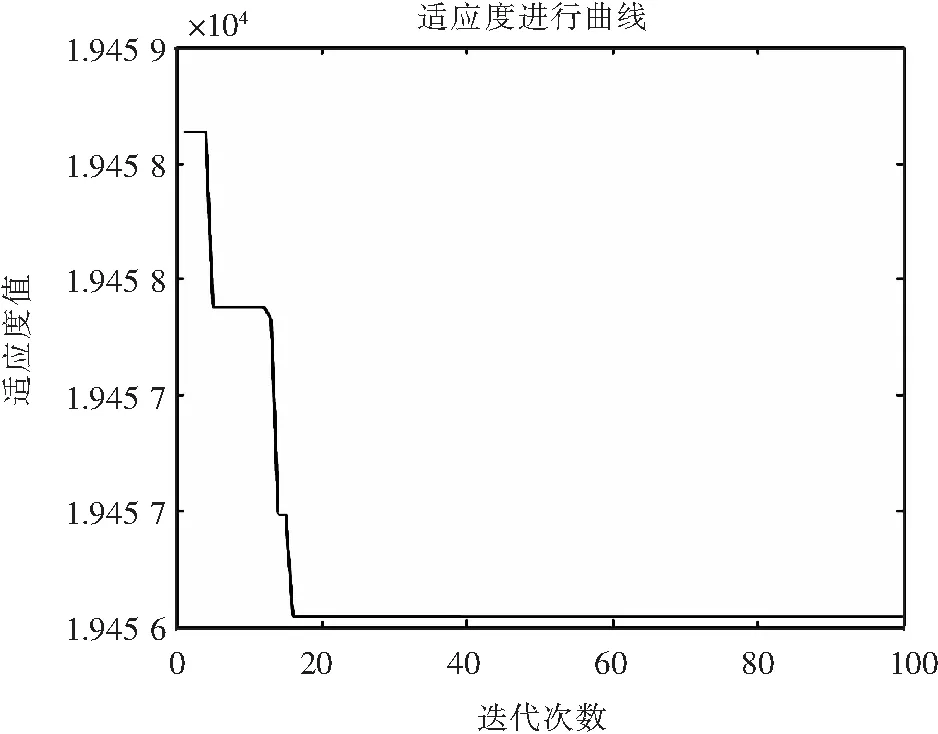
图3 适应度进化曲线
4.2 粒子群算法参数分析
分别调整粒子群算法的参数以分析其对配置结果和算法性能的影响。
4.2.1 学习因子c1、c2的变化
保持其他参数不变,分别将[c1、c2]调整为[2.0 2.0]、[1.5 2.5]、[2.5 1.5],配置结果以及算法的收敛性对比如表2所示。
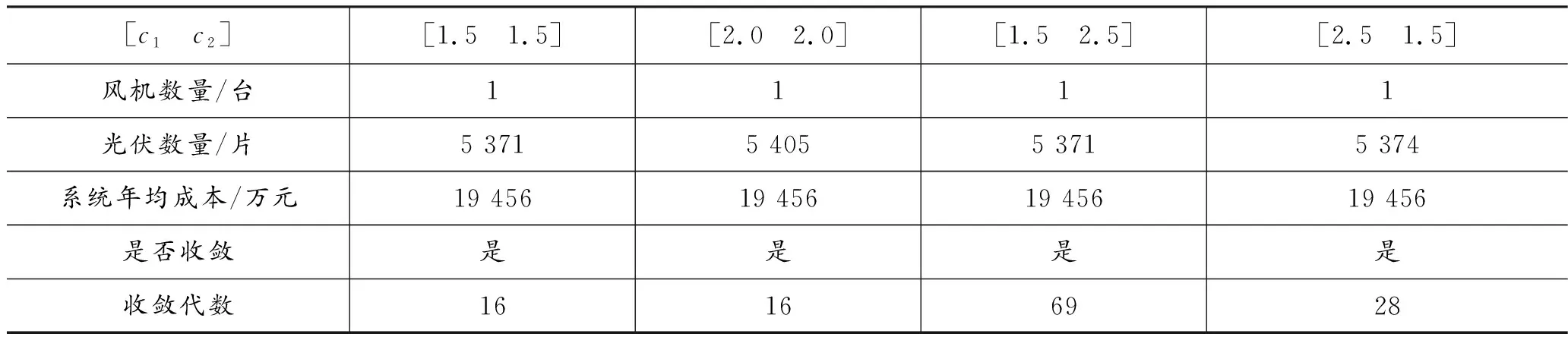
表2 学习因子对粒子群算法的影响
可以看出,当c1、c2调整之后,对优化结果的影响不大,对算法的收敛性会有一定的影响。
4.2.2 惯性权重系数ω的变化
保持其他参数不变,分别将惯性权重系数ω调整为0.6、1.0以及随迭代次数线性递减的惯性权重系数。线性惯性权重系数的表达式为:w=wmax-g(wmax-wmin)/gmax,其中最大惯性系数wmax=0.8,最小惯性系数wmin=0.2,g为当前迭代次数。配置结果及算法的收敛性对比如表3所示。
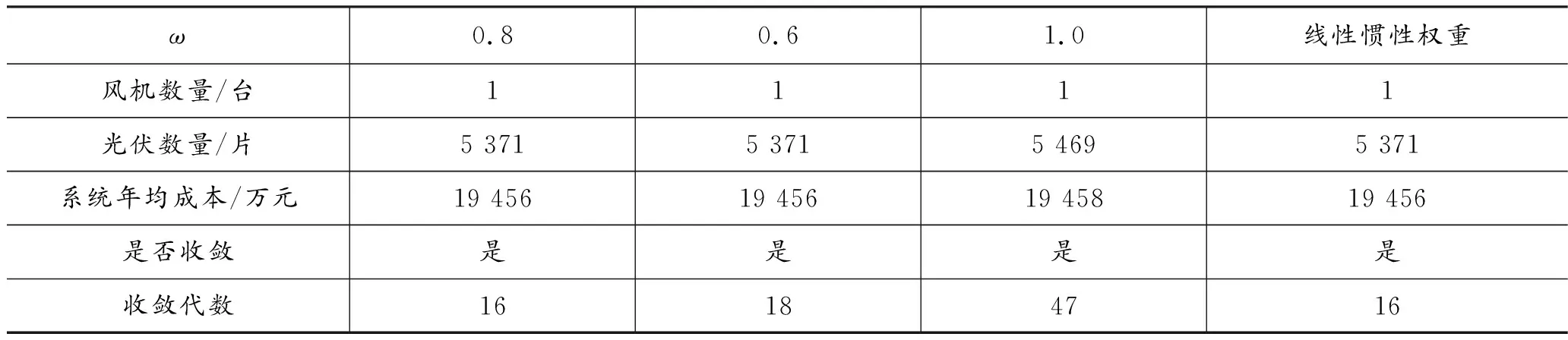
表3 惯性权重系数对粒子群算法的影响
可以看出,将ω调整为1.0时,收敛速度较0.8时慢,且优化结果不如0.8时的好。ω=0.6和线性惯性权重对优化结果和算法收敛性的影响不大。
4.2.3 种群规模M的变化
保持其他参数不变,分别将种群规模M调整为50、150,配置结果以及算法的收敛性对比如表4所示。

表4 种群规模对粒子群算法的影响
可以看出,当种群规模M调整为50时,配置得到的结果没有M=100时的更优,且收敛速度较慢。当种群规模M调整为150时,配置得到的结果与M=100时的相同,收敛速度相差不多。
4.2.4 速度范围的变化
保持其他参数不变,分别将速度的上限调整为[0.5 50]、[1 500]、[1 1000],下限为其对应的相反数,配置结果以及算法的收敛性对比如表5所示。

表5 速度范围对粒子群算法的影响
可以看出,速度范围主要影响算法收敛性。当设置较小的速度范围时,算法的收敛性较好。当设置较大的速度范围时,算法的收敛性较差。
4.2.5 迭代次数的变化
保持其他参数不变,将迭代次数gmax分别调整为50、150、200次,配置结果以及算法的收敛性对比如表6所示。

表6 迭代次数对粒子群算法的影响
可以看出,过大或过小的迭代次数都会影响优化结果。迭代次数为100和150时的优化结果相差不大,但100时的收敛性更好。
4.3 联络线功率限制Pline,max对配置结果的影响
保持其他参数不变,调整联络线功率限制Pline,max分析其对配置结果的影响。由于燃机系统需要满足热负荷,其配置结果基本不变,此处主要分析对风光配置结果的影响,结果如表7所示。

表7 联络线功率限制对配置结果的影响
可以看出,当联络线功率限制过小时,无法配置出能够满足约束条件的容量,因为此时即便风光满装也无法满足约束条件,售电或购电会产生联络线功率越限的情况。当联络线功率限制逐渐增大时,局域能源互联网与电网之间允许交换的功率增大,此时风光的配置数量可以适当减小,功率缺额靠购电满足,功率盈余可以卖向电网。当联络线功率限制大到一定程度以上时,配置结果趋向于不装风光,即除了燃机的出力外,剩余的负荷功率全部由向电网购电来满足,且这种配置结果下的系统年均成本最小。
5 结论
本文在介绍局域能源互联网概念的基础上,以局域能源互联网系统年均成本最小为优化目标,建立了分布式电源优化配置的数学模型,采用粒子群算法进行求解,并进一步分析了算法参数和联络线功率限制对配置结果和算法性能的影响。研究结论如下。
1)本文所提分布式电源优化配置数学模型,能够给出经济性较好的分布式电源配置方案,有效降低系统年均成本。
2)在粒子群算法的参数中,学习因子、速度范围主要影响算法的收敛性,惯性权重系数、种群规模、迭代次数主要影响优化结果。
3)联络线功率限制会影响优化配置结果。过小的联络线功率限制将导致无法配置出满足约束条件的方案,随着联络线功率限制的增大,风光的配置数量逐渐从上限向下减小,最终至0,系统的年均成本也逐渐减小,说明从电网购电比装风光更经济。
