利用等维新息灰色模型的互联网人数预测方法

刘 樱，李月明，柯紫云

(西安欧亚学院，陕西 西安 710061)

1 概述

伴随 “互联网+”行动的兴起，互联网对于整体社会的影响已进入到新的阶段。网络规模持续扩张，互联网用户人数日益增长，使得互联网的影响不断扩大，并且成为社会的重要基础设施。通过对我国互联网用户人数的分析预测，可以对国家和企业掌握互联网的动态发展情况进行相关决策提供十分重要的依据[1]。

目前，互联网用户人数预测模型主要有Bass模型法、回归分析法、BP神经网络预测法等[2-4]。Bass模型法参数确定运算量大，复杂度高；回归分析法需要大量的样本；BP神经网络预测法建立和训练神经网络的过程复杂，运算量大。另外，针对互联网用户人数这种小量且规律相当复杂的数据，很多数据挖掘技术很难发挥其自身优势。

邓聚龙提出灰色模型(GM，Grey Model)，是一种用于有效处理小样本、贫信息、不确定性问题的一种方法[5]。灰色系统理论认为：一切随机变量或随机过程都可以看做在一定范围内、一定时段上变化的灰色量或灰过程，处理灰色量，不是对它的统计规律和概率分布的寻求，而是借助数据来探寻数据之间的规律，从而将其变成比较有规律的数据序列，再建立模型进行预测。文献[6]应用灰色预测与马尔可夫链理论结合来预测交通事故，通过无偏灰色预测模型拟合系统的发展变化趋势，并以此进一步进行马尔可夫预测，在逐步预测中持续推陈出新，更新原始数据。文献[7]利用灰色新城代谢模型对建筑废物输出进行预测。文献[8]用灰色预测模型预测天然气消耗。目前，最常用的灰色模型为GM(1，1)模型，此模型在科技[9]、农业[10]、经济[11]、城市化[12]等各个领域被广泛应用。然而，传统的GM(1，1)灰色预测模型的精度有时难以达到要求，究其原因主要有：一是发展系数和灰色作用量的值依赖于原始序列和背景值的构造形式；二是使用GM(1，1)模型预测时，仅考虑过去的全体数据，未充分利用新信息，因而导致精度较高的仅仅是原点数据以后的1或2个数据。

近年来，众多学者致力于寻找改进GM(1，1)模型来提高其预测精度的方法，例如初始条件优化的近似指数序列灰色建模方法[13]。通过这些方法的使用，虽然GM(1，1)模型的预测精度一定程度上得到提高，但并没有从根本上对GM(1，1)模型进行改进。基于此，本文通过重构背景值和等维新息的思想对传统的灰色预测模型进行两次改进，建立背景值重构的等维新息灰色模型。

2 灰色GM(1，1)模型

2.1 建模原理

灰色模型具有微分、差分、指数兼容的性质，即灰色模型是通过建立差分方程，进而推导出微分方程，且最终求得具有指数性质的时间响应函数，进而对原始数据进行拟合和预测。GM(1，1)模型有3个基本操作：累加生成(AGO)、灰色建模和反向累加生成(IAGO)。

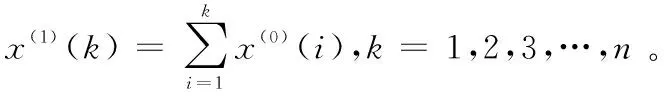
z(1)={z(1)(1)，z(1)(1)，…，z(1)(n)}，
z(1)(k)=(x(1)(k-1)+x(1)(k))/2
k=2，3，…，n

(1)

设x(1)满足：

dx(1)/dt+ax(1)=b

(2)

其中，a代表发展系数，b代表灰色作用量。对应的灰微分方程形式为：

x(0)(k)+az(1)(k)=b，k= 2，3，…，n

(3)

通过最小二乘法估计

(2)式的离散解为：

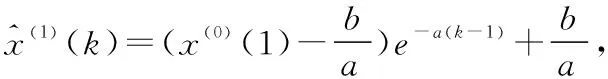
(4)

将上式累减还原，即可得到预测值：

(5)

2.2 模型的检验

众所周知，对未来数据进行预测是建模的主要目的，则评判模型效果的核心指标是拟合的精度。越高的模型的精度，展示的是越好的预测效果。若模型的精度差，则对后期数据的分析处理将毫无意义，所以对模型精度的评定是非常有必要的。因此，灰色预测模型必须先通过精度检验再决定其是否可以用于模拟、预测。模型精度的检验参数主要有2个：绝对误差AE(k)、平均相对误差MAE，分别定义为：

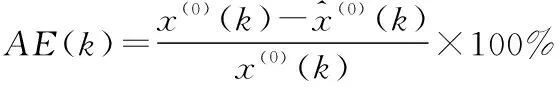
3 背景值重构的灰色模型

由(4)式可以看出，GM(1，1)模型的模拟及预测精度取决于发展系数a与灰色作用量b，而由(3)式能够得知，求解a和b的数值依赖于背景值的构造方式。所以影响GM(1，1)模型精度的关键因素之一就是背景值的构造方法。

图1描述的是背景值误差，在区间[k-1，k]上对(1)式两边同时求积分可得：

图1 背景值误差的描述

背景值重构的思路[11]：由(4)式可知x(1)(t)为非齐次指数函数，不妨将x(1)(t)抽象为

x(1)(t)=Bexp (At)+C

(6)

(7)

当t=1时，有x(1)(1)=x(0)(1)，即

BeA+C=x(0)(1)

又由于

x(0)(k)=x(1)(k)-x(1)(k-1)=BeAk-BeA(k-1)

可得：

(8)

对上式进行化简得：

最后求得：

A=lnx(0)(k)-lnx(0)(k-1)

(9)

将(9)式代入(8)式得：

(10)

其中L(k)=lnx(0)(k)-lnx(0)(k-1)。

将(9)、(10)式代入(7)式得：

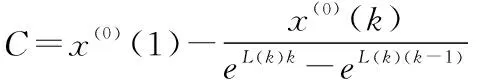
(11)

最后将式(9-11)代入式(6)得到新构造的背景值计算公式为：

(12)

其中L(k)=lnx(0)(k)-lnx(0)(k-1)，k= 2，3，…，n。

由以上分析可知，重构的背景值减小了传统模型背景值所产生的误差。

4 背景值重构的等维新息灰色模型

对灰色系统来说，干扰系统的因素和系统的状态都会随着时间的变化而不断变化。传统的灰色预测模型下原点数据以后的1～2个数据准确度较高，随着时间推移，离时间原点越远，模型的预测精准度越低。所以，系统的变化和状态必须由引入已知信息来反映，或在全未知信息的状态下，由灰色信息来淡化灰平面的灰度，这种模型通过及时地加入了新的已知信息或灰色信息、删除旧的数据，因而可以较准确地反映系统的变化状态，故称为新息灰色模型[14-16]。但是灰色GM(1，1)模型长期预测的有效性受时间序列长短和数据变化的显著影响，若数据序列太短，则长期的预测模型难以建立；序列太长，系统受干扰的成分变大，将增多不稳定因素，系统预测精度下降。因此通过在GM(1，1)模型中引入等维约束条件，构建等维新息GM(1，1)模型，能够弥补灰色系统模型的不足，使得预测预报的精度有效提高[17]。

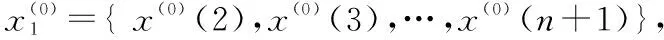
5 实例分析

自1997年以来，CNNIC开展统计调查工作已有22年，并于每年1月、7月分别发布统计报告2次，发布我国因特网上用户人数、信息流量分布、用户分布、上网计算机数、域名注册等方面的统计信息情况。这给我国信息化发展提供了重要的咨询，同时给政府、机构和企业各界提供了关键的决策参考。根据中国互联网信息中心(CNNIK)第44次发布的《中国互联网络发展状况统计报告》[1]，截至2018年12月，中国网民规模达8.26亿，互联网普及率达61.2%。本文选取CNNIC于2019年7月发布的第44次报告数据(见表1)，以我国互联网用户人数为例进行分析。取2010-2015年的数据组成原始序列，在3种不同方案下运用MATLAB 预测2016-2018年的互联网用户人数。

表1 2007-2015年我国互联网用户人数

灰色GM(1，1)模型。利用灰色系统建模方法，对2010-2015年的数据构建灰色GM(1，1)模型。解得：a=-0.145 1，b=27 116。由此得到我国互联网用户人数的传统灰色GM(1，1)模型为：

表2 传统GM(1，1)模型的预测结果

背景值重构的GM(1，1)模型。对2010-2015年的数据构建背景值重构的GM(1，1)模型，解得：a1=-0.133 1，b1=27 960。得到我国互联网用户人数的背景值重构的GM(1，1)模型为：

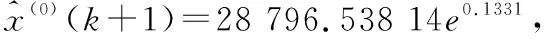
表3 背景值重构的GM(1，1)模型的预测结果

由表2～表4可以看出，背景值重构的等维新息灰色预测模型的预测精度最高，它的平均相对误差约比背景值重构的GM(1，1)模型减少约2.30%，比传统GM(1，1)模型减少5.83%，效果较好。

表4 背景值重构的等维新息GM(1，1)模型的预测结果

对比各模型预测值与实际值可知，在互联网用户人数预测过程中，传统GM(1，1)模型的预测结果只能反映用户人数的大致趋势；背景值重构的GM(1，1)模型在传统GM(1，1)模型基础上做了改进，预测精度高于GM(1，1)模型；而背景值重构的等维新息GM(1，1)模型则是将2013年的实际值加入到系统中，去除了老数据，使预测精度进一步提高。因此，背景值重构的等维新息GM(1，1)模型可以更好地预测互联网用户人数。

6 结语

本文在白化方程上利用积分重构的方式构造了GM(1，1)模型的背景值，减少了传统背景值对模型造成的误差，提高了模型的精度。接着在背景值重构的前提下，实时地加入了新的信息，建立等维新息GM(1，1)模型。结合第37次中国互联网络发展状况统计报告的数据，通过仿真分析对互联网用户人数进行灰色建模并进行预测，结果表明：使用背景值重构的等维新息GM(1，1)模型的预测准确率明显高于背景值重构的GM(1，1)模型和传统GM(1，1)模型。