有限维非退化可解李代数顶点算子代数模的结构

范 洪 霞

(哈尔滨商业大学 基础科学学院，哈尔滨 150028)

顶点算子代数起源于数学中的魔鬼群表示、月光猜想和物理学中的共形场理论.顶点算子是顶点算子代数结构中的核心部分，它最早出现在物理学的弦理论中.为了描述弦之间的相互作用，物理学家引入了一种局部算子，即某种顶点算子.在弦理论和共形场论中，弦之间的相互作用是由顶点算子在一个无穷维向量空间上的作用来表示.在某种意义下，顶点算子是场算子的代数描述.

R·E· Borcherds[1]首次引入了顶点代数的数学定义，这标志着顶点代数理论的诞生.1988年，Frenkel L, Lepowsky和Meurman[2]引入了顶点算子代数的概念.至今顶点算子代数理论已有完备公理体系和结构及表示理论.Frenkel I和Zhu[3]分别构造了许多顶点代数例子.Meurman,Primc[4]、Xu[5]构造了一些Virasoro代数、Heisenberg代数、仿射李代数、格相关的顶点代数的例子.李海生[6-8]等人给出了素特征域上仿射顶点代数的扭模，建立了一些经典代数(如双杨氏代数)同量子顶点代数的自然联系以及探索了三角李代数、仿射李代数、顶点代数的内在联系.姜翠波,林宗柱[9]用范畴的语言对顶点算子代数理论中的一些构造加以解释.李杨[10]素特征域上顶点代数的局部系.程俊芳,楚彦军[11-12]给出了扭的Heisenberg-Virasoro顶点算子代数的一个特征.王书琴[13-15]构造了相应于非退化可解李代数的顶点算子代数以及它的一类子代数结构.本文研究相应于非退化可解李代数的顶点算子代数的模的结构性质.并且得到了以下结果: 仿射李代数的水平为的限制模与顶点算子代数模一致；的顶点算子代数的不可分解模存在子模的合成列.

φ∶→EndWa⊗tn|→φ(a⊗tn)=aW(n),

K|→φ(k)=l·1W

(1)

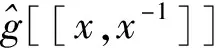
YW(a,x)

(2)

换位运算可等价表示为

(3)

[YV(a,x1),YV(b,x2)]=

YV((YV(a,x1-x2)-YV(a,-x2+x1))b,x2)=

(4)

a⊗tn|→=a(n)=aV(n),k|→l

(5)

ψ(a(x))=aV(x)=YV(a,x)

(6)

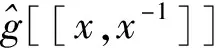
[YV(a,x1),YV(b,x2)]=

(7)

比较式(6)、(7)有：

i=0,a0b=[a,b];i=1,a1b=l;i≠0,1,aib=0.

(8)

[YW(a,x1),YW(b,x2)]=

(9)

将式(8)代入得

(10)

即

φ([a(x1),b(x2)])=[φ(a(x1),φ(b(x2))],φ[a⊗tn,b⊗tm]=[φ(a⊗tn),φ(b⊗tm)].

(11)

aW(x)nbW(x)=Eesx1((x1-x)naW(x1)bW(x)-(x1-x)nbW(x)aW(x1)),

(12)

aW(x)nbW(x)∈ε(W)，

令

UW(x)=span{aW(1)(x)n1…aW(r)(x)nr1W|a(i)∈g,ni∈Z,r≥0}.

规定

Yε(x)(aW(1)(x)n1…aW(r)(x)nr1W,x0)=

a(1)(x0)n1…a(r)(x0)nr1W.

(13)

YW(x)(aW(1)(x)n1…aW(r)(x)nr1,x0)=

a(1)(x0)n1…a(r)(x0)nr1W.

(14)

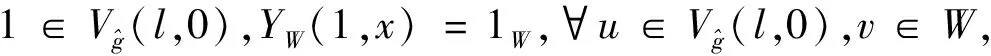
由Yε(·,x0)满足Jacobi 等式

YW(x)(aW(1)(x)n1…aW(r)(x)nr1,x0)=

Yε(aW(1)(x)n1…aW(r)(x)nr1W,x0)

(15)

所以YW(·,x0)也满足Jacobi等式，综上(W,YW)是一个顶点代数模.

(16)

由PBW定理

M(l,W)={a(1)(-m1)…a(r)(-mr)u|r≥0,a(i)∈g,mi≥1,1≤i≤r,u∈W}.

(17)

(18)

(19)

其中

(20)

并且

[L(m),a(n)]=-na(m+n),

(21)

[L(m),L(n)]=(m-n)L(m+n)+

(22)

由定理1.1知M(l,W)是顶点代数模.记L(n)=LM(n),a(m)=aM(m)因为模作用乘法保持换位运算，所以式(21)、(22)在M(l,W)也成立,且

(23)

(24)

(25)

所以

(hM+n)v}.

(26)

下面讨论作为顶点算子代数模M(l,W)的合成列.

定理1.3 设W是非退化可解李代数g的有限维模,诱导模M(l,W)作为顶点算子代数模, 那么

1)存在顶点算子代数模Mi,i=1,…,t.使

M(l,W)=Mt⊃Mt-1⊃…M1⊃M0=0

(27)

2)不存在顶点算子代数真子模M,使MiMMi-1(i=1,…,t)成立.

证明1)W是有子模合成列

W=Wt⊃…W1⊃W0=0 dimWi/Wi-1=1

(28)

构造诱导模

(29)

由式(28)得

M(l,W)=Mt⊃Mt-1⊃…M1⊃M0=0

(30)

2)若存在顶点算子代数模M,使MiMMi-1,i=1,…,t.则有

(31)

又g=g⊗t0,∀a∈g,a=a(0),a∈g,v∈M(h+n),n∈N,L(0)v=(h+n)v,则有

L(0)av=L(0)a(0)v=a(0)L(0)v+[L(0),a(0)]v=a(0)L(0)v=(n+h)a(0)v=(n+h)av

(32)

所以

g·M(h+n)⊂M(h+n)

(33)

从而每个齐次子空间M(h+n)都是g模.最低权空间M(h)是g模.若M(h)⊄Wi,必存在u∈M(h),u∉Wi,从而u∈M(h),u∉Wi从而

(34)