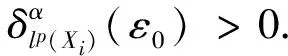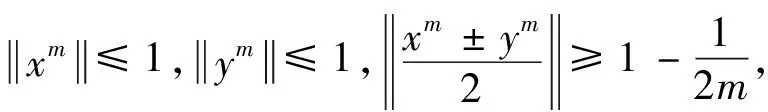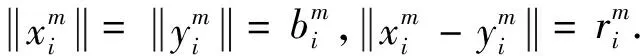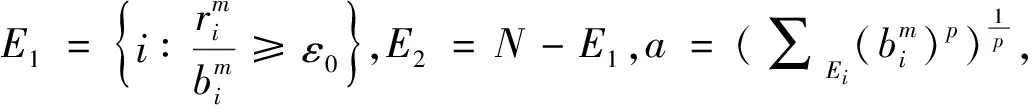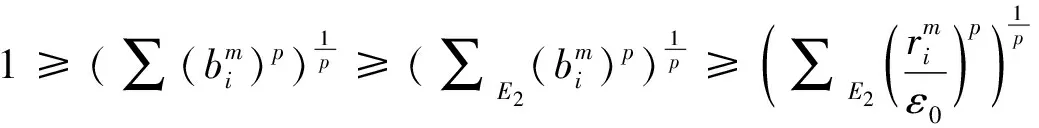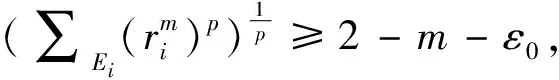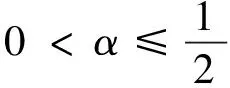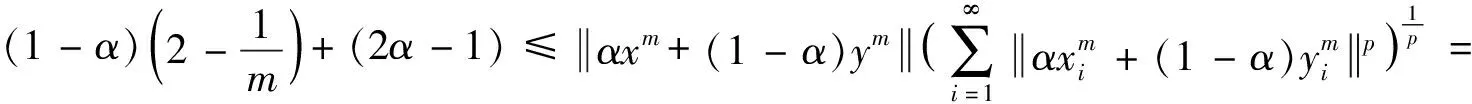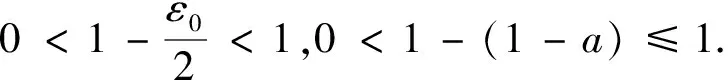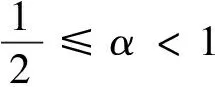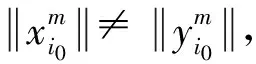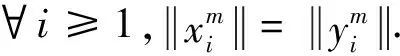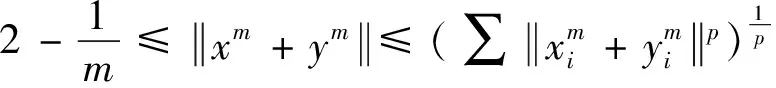广义凸性模与一致非方空间

赵 亮，韩朝阳

(哈尔滨理工大学 理学院，哈尔滨 150080)

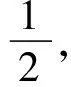
1 基本定义

本文以X表示Banach空间，用S(X)来表示X的单位球面，l(c)表示Banach空间X中的线段c的长度.

定义1[1]函数δX(ε)∶[0,2]→[0,1],

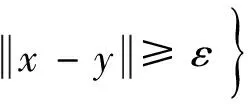
定义2[2]Banach空间为一致非方：如果存在正数δ，使得对单位球中所有的点x,y有

定义3[4]函数

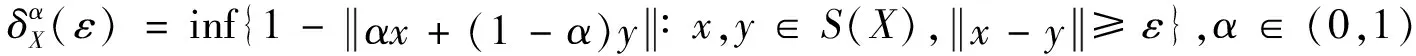
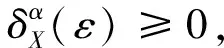
引理1[7]

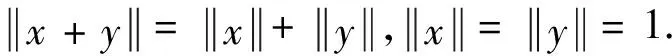
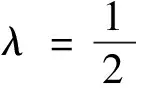
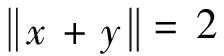
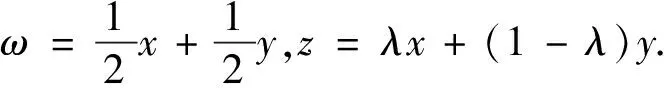
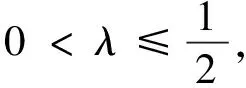
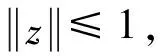
2 主要结果

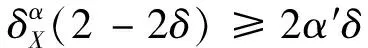
其中α′=min{α,1-α}.

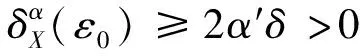
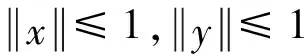
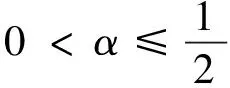
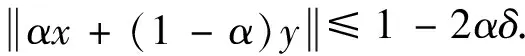
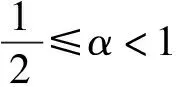
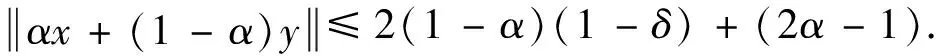
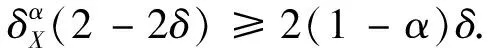
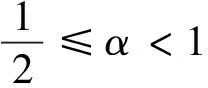
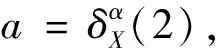
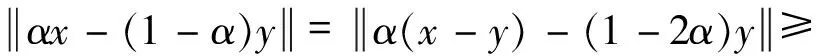
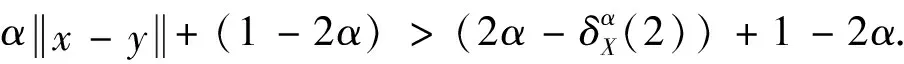
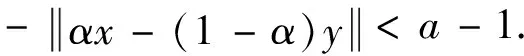
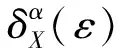
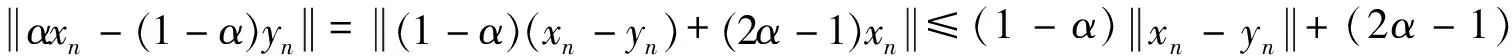
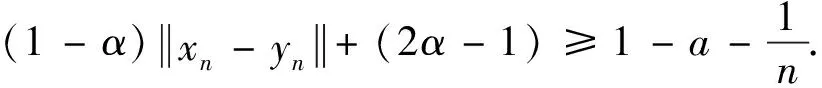
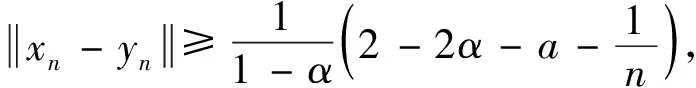
综上所述，结论得证.

我们知道一致非方空间的子空间也是一致非方的，所以若lp(Xi)(1

(1)

(2)

由式(1),(2)可知

令m→∞,

(3)

所以

与式(3)相矛盾，故假设不成立.

同理可证.

令：

现将xm,zm分别视为(ⅰ)中的xm,ym由于ε可取任意小，m可取任意大，所以仿照(ⅰ)的讨论，得出矛盾.

综上所述，充分性得证.