基于Midas对梁桥温度荷载试验研究

谢栋明，王艳军

(福建农林大学 金山学院，福州 350000)

自然环境的温度和太阳光的辐射会导致梁体外表面温度快速变化，而结构内部的温度一直不变或者变化很小，这种结构的内外温差就形成了温度梯度，温度的散失会在结构的材料中形成非线性温度分布状态，让整个结构每个部位的温度状态各有不同.当存在温差时结构会产生形变，变形受到约束时，产生的温度应力就要重视.有些温度导致的应力相当于活荷载产生的应力，会导致结构产生裂损，给桥梁的安全运营带来危险[1].

1 国内外研究现状

2004年国外学者Thomas 用FETAB软件分析了混凝土T形梁的温度效应并且与现场实测数据对比分析，结果表明：梁体表面对流换热系数的确定是影响计算结果准确性的主要原因之一；2008年国外学者Diger W H与Mase M A对加拿大跨径为200 m 的混凝土T形梁桥进行了连续观测及研究，结果发现加拿大桥梁设计规范对T形梁横向温差的规定不适用于所有的梁桥，至少对于所观测桥来说是相对不安全的[2-5].

2005年湖南大学方志对混凝土斜交T形梁进行了温差的实际测量，根据实际测量的数据分析并总结出了斜交T形梁的温度场变化规律，并推断出了适用于中国中西部地区的温度梯度模式[6]；2012 年，程海根和王美英建立了某简支桥梁二维模型，根据模型采取了温度应力计算和太阳光照温度场的分布情况，现场试验与计算结果分析对比，结果表明：温度作用所产生温度应力是不能忽略不计的[7].

2 通过Midas-civil建立梁桥温度荷载试验有限元模型

2.1 建模依据

依据桥梁检测荷载试验来测量桥梁在其影响下的相关参数.温度荷载试验主要是研究升温和降温时桥梁结构内力和应变的变化.本文研究结合桥梁结构Midas-civil有限元分析软件和现场实际试验数据，模拟出斜交T形梁桥进分析，为桥梁载荷试验提供了有力依据.

2.2 建立梁桥有限元模型

实例采用梁格法建立有限元模型, 桥梁纵向为X轴，横桥方向为Y轴，桥梁垂直方向为Z轴，坐标系选取默认坐标系，单位系选取t/m，并根据桥梁的几何尺寸建立结构模型.有限元模型如图1所示.

图1 梁桥有限元模型示意图

材料：采用外径D=70 mm的圆形塑料波纹管；C50的混凝土；预应力钢绞线直径为15.2 mm，单根钢绞线截面积为AP=140 mm2，抗拉强度标准值为1 861 MPa，钢筋与管道壁的摩擦系数μ=0.17，管道每米局部偏差对摩擦的影响系数K=0.002，预应力钢绞线松弛系数&=0.35;钢筋采用HRB335直径D=12 mm和HRB335直径D=25 mm的钢筋.

结构：共有5个横隔板，有3个是中横隔板，2个为端横隔板，横隔板都是倾斜放置；横桥向布置5片梁，共计125个节点,110个梁单元，84个板单元，标准跨径为30 m、斜交角度30°.

3 施加温度荷载的有限元模型分析

3.1 温度梯度

温度梯度是指桥梁结构在受到太阳辐射的影响之后，桥主梁部分的温度顺着梁高度方向变化的模式.把温度梯度模式大致可以分为两类：线性温度变化模式和非线性温度变化模式.如图2所示.

图2 温度梯度示意图

3.1.1 线性温度变化

桥结构的主梁结构在线性温度模式下产生弯曲变形.在静定结构情况下，线性温度变化会引起桥梁结构的位移变形；而在超静定结构情况下，因为有了多余约束的影响，桥结构才会产生温度次内力[8-10].

3.1.2 非线性温度变化

在静定结构情况下，非线性温度梯度会让桥梁结构产生弯曲变形；在超静定结构情况下，多余约束阻止了桥梁结构发生变形产生的应力即为温度次内力[11].

3.2 温度梯度效应的研究

在分析试验桥梁的温度梯度效应时，通过计算得到的温度梯度以温度荷载的形式应用到计算模型中[12].当加载温度荷载时，有限元模型软件MIDAS-civil仅允许加载线性的温度梯度，因此要把非线性温度梯度等效成线性温度梯度进行加载试验.将垂直和横向温度梯度作为荷载应用于有限元模型中予以施加[13].

结构竖向温度梯度可等效为：

T(y)=17.9……y=0

13.0……y=0.1

6.84……y=0.3

3.6……y=0.5

0……y=1.2

(1)

其中：T(y)是拉杆中每个点的温差值，它是坐标y的函数，单位℃；y为该点距离梁顶的距离，单位m.

在最不利的温度分布下，结构的横向温度梯度可以相当于：

T(x)=6……x=0

2……x=0.15

0……x=3

0……x=1.1

0……x=1.25

(2)

其中：T(x)为连接腹板的点和腹板边缘之间的温差，它是坐标x的函数，单位 ℃；x为该点距离梁顶的距离，单位 m.

3.3 荷载工况

为了直观的分析桥梁上不同方向的温度梯度的影响，以下两种荷载工况来进行研究：

工况1：主梁控制截面的内力和应力，施加温升20 ℃梯度荷载；

工况2：主梁控制截面的内力和应力，施加温降20 ℃梯度荷载.

3.3.1 在工况条件1作用下，主梁控制截面的内力和应力

测试结果与数值计算之间的比较如图3～5和表1、2所示.由图4、5可以看出边梁的跨中弯矩最大，是最容易出现裂缝的位置.当在荷载工况1作用时，是以边梁为主要受力点.由表1可知：在荷载工况1条件作用下，边梁所产生的轴向力是压力，并且从端部向中部逐渐减小，在顺桥方向边梁跨中的截面出现最大弯矩值为936.71 kN·m.

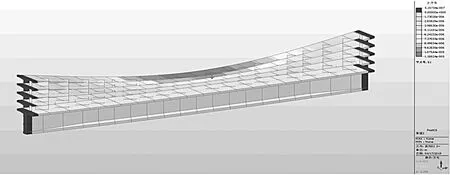
图4 中跨左边梁弯矩图

图5 中跨右边梁弯矩图

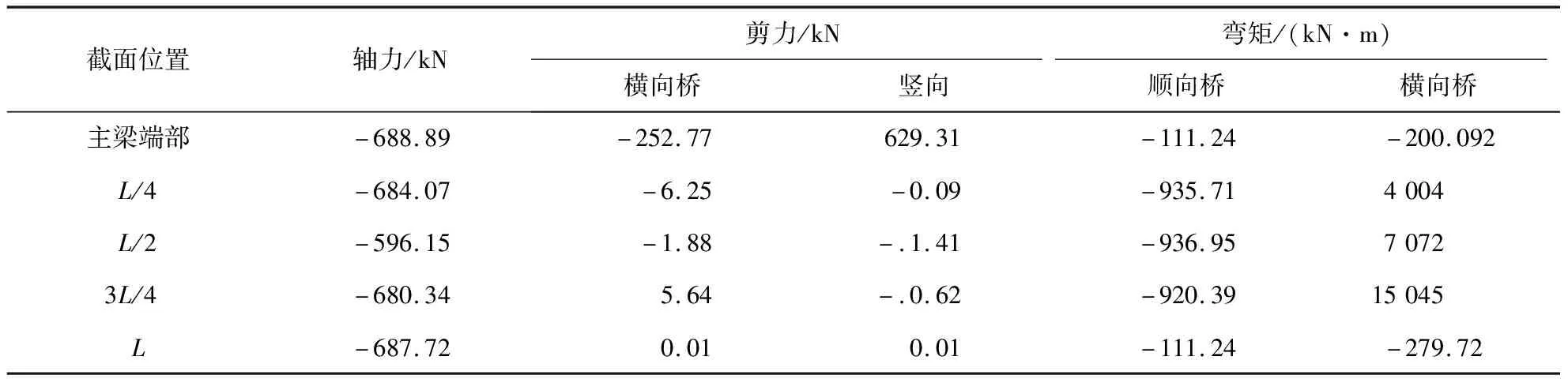
表1 边梁控制截面内力

由表2可知：在荷载工况1条件作用下，在截面上边缘出现最大应力值为5.23 MPa.

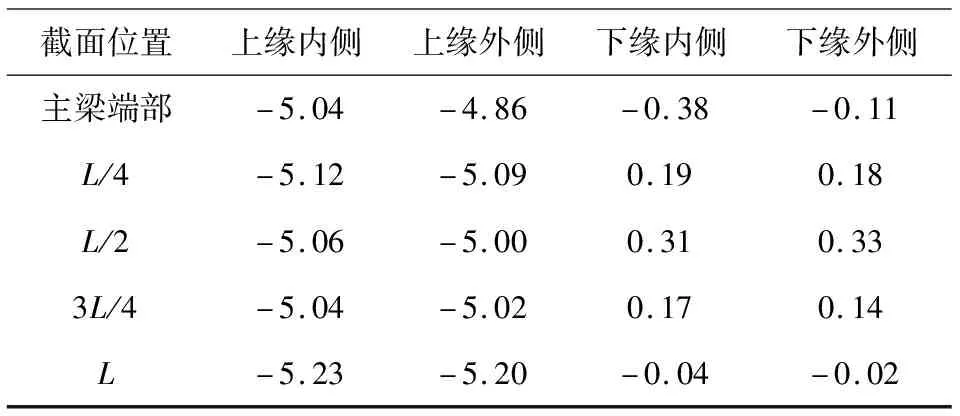
表2 边梁控制截面应力

根据工程概况和实际经验提出一些对温度变化引起的混凝土变形裂缝的处理意见：

1)有效设置后浇带：具体工程应结合建筑物的长度、气候环境特点综合考虑，一般控制在20m左右、宽度在考虑满足钢筋错开搭接的要求下，预留出1 m的宽度、浇筑时的温度要比主体浇筑时的温度低、后浇带混凝土要采用高于两侧混凝土一个等级的无收缩或微膨胀混凝土.

2)局部加强配筋：实际配筋要考虑温度收缩应力影响予以适当的增大，在边跨的位置要设置腰筋.

3)设置伸缩缝：在跨中位置设置垂直于顺桥方向的伸缩缝.

3.3.2 工况条件2下主梁控制截面内力和应力

试验结果与数值计算的对比分析如图6、7和表3、4所示.

图6 轴力图

图7 中跨弯矩图

表3 中梁控制截面内力

由图6、7可以看出,中梁的跨中弯矩最大，是最容易出现裂缝的位置.当在荷载工况2作用时，是以中梁为主要受力点.

由表3可知：在荷载工况2条件作用下，中梁所产生的轴向力是拉力，最大值出现在主梁L/4位置，其值为688 kN，轴力最小出现在主梁端部，其值为320.42 kN.在顺桥方向的中梁的跨中截面出现最大弯矩值为936.47 kN·m.

由表4可知：在荷载工况2作用下，应力最大截面出现在截面上缘内侧，最大值为5.23MPa.

表4 中梁控制截面应力

4 结 语

通过温度荷载工况作用下可以看出，斜交T形梁桥受温度影响很大，跨中产生很大的弯矩与剪力，因此跨中板面处是最容易出现裂缝的位置.外观检查中发现的桥面铺装及主梁病害均与此有关.

在温升20 ℃的梯度作用下，边梁跨中和中梁跨中所产生的轴向力是压力，在控制截面应力方面，边梁跨中和中梁跨中均在截面上边缘内侧产生较大的应力，在顺桥方向边梁跨中桥板面会受拉，板底受压，导致该桥的边梁跨中板上表面起拱度极大，最容易出现裂缝；在温降20 ℃的梯度作用下，边梁跨中和中梁跨中所产生的轴向力是拉力，在控制截面应力方面，边梁跨中和中梁跨中均在截面上边缘内侧产生较大的应力，在顺桥方向中梁跨中桥板面会受压，板底受拉，导致该桥的跨中板底最容易出现裂缝[14-15].

当混凝土桥梁因温度应力大于自身的抗拉强度时，就会产生温度裂缝，通过本文的研究分析，以期在今后的桥梁设计施工中，要按规范结合经验，采取相应的裂缝控制措施来增加桥梁的使用年限.