基于特征向量重叠特性的伪码序列盲估计
2020-08-31张润雨
张润雨,高 勇
(四川大学 电子信息学院,四川 成都 610065)
0 引言
直接序列扩频(DS-SS)采用了伪随机序列调制,将信号所占带宽扩大,而且功率谱密度很低,使得直接扩频序列具有低截获率和抗干扰的优点,在各个方面都有广泛应用。
目前,已有大量文献研究了短码直接扩频序列的伪码估计。文献[1]提出了一种Massey算法来估计伪码序列,但该方法在低信噪比下效果恶化。文献[2-5]利用单倍周期分段构造相关矩阵,再进行奇异值分解或特征值分解来估计伪码序列。文献[6-8]提出了一种基于子空间跟踪的扩频序列估计方法,降低了运算量和存储量。本文把采用双倍PN码周期分段的压缩投影逼近子空间算法称为DPASTd算法。文献[9-14]采用二倍伪码周期分段的方法构造相关矩阵,再进行奇异值分解或特征值分解来估计出PN码。其中,文献[10]的算法称为EVD算法;文献[11]的算法称为SVD算法,得到的最大特征向量的符号函数就是要估计的PN码。但是当时延十分接近一周期完整扩频码的首端或尾端时,就会存在最大特征向量与次大特征向量相近的酉模糊问题。针对此问题,本文利用分段后特征向量存在重叠的特点,结合最大特征向量和次大特征向量的线性关系,将相近的最大特征向量与次大特征向量明显地区分开来,解决之前方法存在的酉模糊问题。理论推导和实验结果均表明该算法有效。
1 信号模型
假设通过高斯白噪声信道后,接收到的DSSS基带信号模型为:
x(t)=s(t)+n(t),
(1)
式中,s(t)为信息部分;n(t)为零均值、方差为σ2的高斯白噪声部分,且
(2)
式中,{ak=±1,k∈Z}为服从等概率随机分布的信息序列;Ts为信息符号周期(也等于PN码周期);τ为在[0,Ts]上均匀分布的随机时延;h(t)为传输链路所有滤波器与一整周期扩频序列的卷积,即:
(3)
式中,{ci=±1,i=0,1,…,N-1}为扩频码序列;p(t)为持续时间为Tc的码片波形;Tc为扩频码码片宽度且Ts=NTc。
2 利用特征向量的重叠特性估计伪码序列及时延
2.1 扩频序列估计
不失一般性,假设已从文献[15-16]的方法中获得信号的伪码周期和码片宽度。本文提出的算法基于与文献[9-14]相同的分段方法,即以2倍信息符号周期为间隔,重叠一个信息符号周期的时间窗进行分段。本文算法信号分段方式如图1所示。

图1 本文算法信号分段方式Fig.1 Signal segmentation method in the proposed algorithm
由图1可知,按照2倍扩频码周期分段,不论时延为多少,每个时间窗内都至少包括一个完整周期的扩频序列,若时延不为零,则每个时间窗内都包含3个信息符号。以码片宽度为采样周期对接收到的信号进行采样可以得到2N×1维观测样本矢量,则观测样本向量可以表示为:
x(m)=a(m-1)hL+a(m)h+a(m+1)hR+n(m),
(4)
式中,hL表示一个时间窗内的第一个信息符号对应的伪码序列;h表示一个时间窗内的第2个信息符号对应的伪码序列;hR表示一个时间窗内的第3个信息符号对应的伪码序列,且均被扩展为2N×1维的向量,则hL,h,hR三者相互正交:
(5)
(6)
(7)
式中,d∈[0,N)表示传输时延对应的离散采样值。假设接收到M+1个信息码序列,则可以得到M个x(m),将其构成2N×M的矩阵为:
X=[x(1)x(2) …x(M)]=
[a(0)hL+a(1)h+a(2)hR+n(1)
a(1)hL+a(2)h+a(3)hR+n(2) …
a(M-1)hL+a(M)h+a(M+1)hR+n(M)]=
hLa0+ha1+hRa2+n,
(8)
式中,n是由n(1),n(2),…,n(M)构成的维度为2N×M的矩阵,
(9)
因为ak为服从等概率随机分布的信息序列,则aiaj(i≠j)也为服从等概率分布的、取值为±1的随机序列[12]。所以
(10)
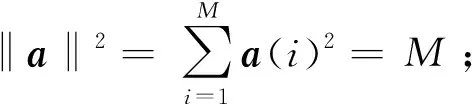
‖hL‖2=N-d,‖h‖2=N,‖hR‖2=d,
(11)
则可以计算接收信号的协方差矩阵:
R=E{XXH}=
E{[hLa0+ha1+hRa2+n]×[hLa0+ha1+hRa2+n]H}=
E{‖a0‖2hL(hL)H+‖a1‖2hhH+‖a2‖2hR(hR)H+σ2I}=
E{MhL(hL)H+MhhH+MhR(hR)H+σ2I}。
(12)
由矩阵论知识可得出R的特征值与特征向量的对应关系如表1所示。
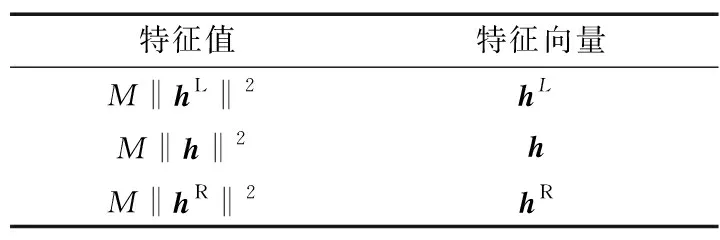
表1 协方差矩阵的特征值与特征向量对应关系

假设经过特征值分解,得到的最大特征向量为U1、次大特征向量为U2(均为2N×1维向量),则有:
(13)
(14)
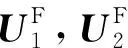
(15)
可写为:
(16)
即
Uq=0,
(17)
式中,

(18)
可以由下式得到q:
(19)
表示q是UHU的最小特征值对应的特征向量,到此求出q,则可以根据对时延的判断通过式(13)或式(14)来求出包含一周期完整的扩频序列的最大特征向量h。
2.2 时延估计
根据观察发现,由于可能存在反相情况:
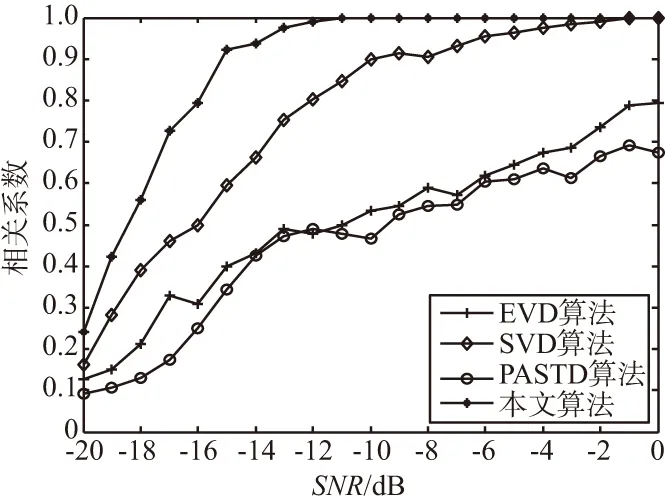
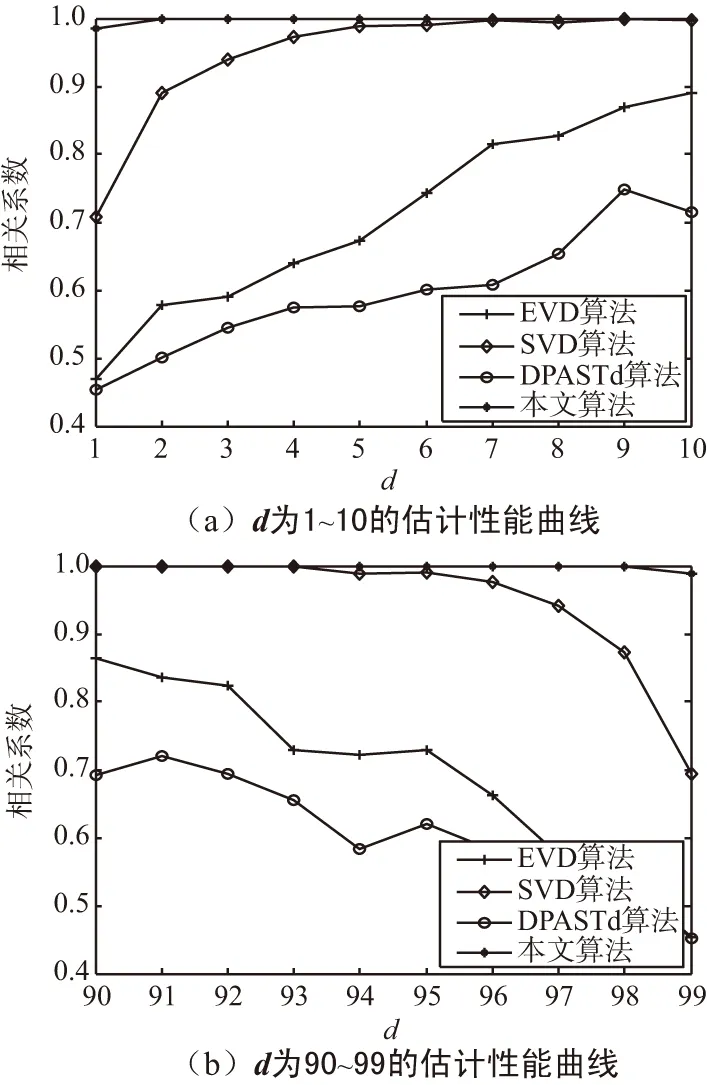
当d (20) 当d>N/2时, (21) 根据该结论可以大概判断出时延的位置,就可具体确定在求出q之后是使用式(13)还是式(14)来求解最大特征向量h。求出最大特征向量后,再利用滑动搜索法求出具体时延。 提出的扩频序列的估计算法步骤如下: 步骤1:对接收到的信号按照Tc进行采样,以2倍的扩频码周期为间隔、50%的重叠率进行分段形成2N×1维观测样本矢量x(m); 步骤2:对M个x(m)构成的2N×M矩阵X的协方差矩阵R进行特征值分解求得最大特征向量U1、次大特征向量U2(也可直接对矩阵X进行奇异值分解求得最大左奇异向量U1、次大左奇异向量U2,2种分解方法等效); 步骤4:d 在后面的仿真实验中,采用相关系数ρ来衡量各算法的估计性能: ρ=abs((S-D)/(S+D)), (22) 式中,S是估计出的扩频码序列与原始的扩频码序列相同的位数;D是估计出的扩频码序列与原始的扩频码序列不同的位数。相关系数越大,说明估计性能越好,相关系数为1时,表明扩频序列全部估计正确。 仿真信号采用的是二进制相移键控(Binary Phase Shift Keying,BPSK)调制的短码直扩信号,信号长度是601个扩频周期,伪码序列的长度为100的截断m序列,则选择τ=2Tc作为时延接近一周期扩频码的始端的情况(也可选取其他接近0的值),信噪比(Signal-to-Noise Ratio,SNR)为-8 dB,采样周期等于Tc。图2~图5是时延τ=2Tc(即d=2)时不同算法估计的最大特征向量。 图2 EVD算法估计的最大特征向量Fig.2 Largest eigenvector estimated by EVD algorithm 图3 SVD算法估计的最大特征向量Fig.3 Largest eigenvector estimated by SVD algorithm 图4 DPASTd算法估计的最大特征向量Fig.4 Largest eigenvector estimated by DPASTd algorithm 图5 本文算法估计的最大特征向量Fig.5 Largest eigenvector estimated by the proposed algorithm 根据理论分析(如式(12)推导)最大特征向量应该具有式(6)的形式,即前面为N-d个零值,中间是完整的一周期PN码,后面为d个零值。然而由于噪声干扰和时延导致的酉模糊,使得最大特征向量被严重干扰。结果表明,使用EVD、SVD、DPASTd算法得到的最大特征向量中属于噪声序列的部分几乎与属于伪码序列部分的幅度相同,给估计出正确的伪码序列带来困难。而本文算法仍具有类似式(6)的形式,其中理论上应为零值的部分在本文算法仿真下为幅度比扩频序列显著小的噪声序列,理论上不为零值的部分在仿真后是比噪声序列显著大的扩频序列,通过最大范数搜索可以正确地估计出伪码序列,可见本文算法是有效的。 实验条件与实验1相同,在SNR=-8 dB时延τ=2Tc(选一个接近零的时延即可)情况下,对使用本文算法估计到的伪码序列与原始伪码序列(为方便比较将原始伪码序列幅值缩小到0.1)进行了比较。比较结果如图6所示。因为时延τ=2Tc,一周期完整的伪码序列位于t∈[99Tc,198Tc]之间,位于t∈[Tc,98Tc]和t∈[199Tc,200Tc]之间的是幅度接近零的噪声序列。可以看出,使用本文算法消除了时延接近零时存在的酉模糊,可以正确估计出原始伪码序列,估计的伪码序列与原始伪码序列一致。 图6 本文算法估计PN序列与原始PN序列Fig.6 PN sequence estimated by the proposed algorithm and the original PN sequence 仿真分别使用EVD、SVD、DPASTd和本文算法在SNR为-20~0 dB下对PN码进行估计,每一个SNR使用300次蒙特卡洛仿真,其他条件与实验1相同。本实验使用的PN码是长度为100的截断m序列,则分别选取τ=2Tc和τ=98Tc作为时延接近一周期扩频码的始端和末端的情况。τ=2Tc和τ=98Tc时,各算法对PN码的估计性能曲线图如图7和图8所示。 图7 时延τ=2Tc各算法的估计性能曲线Fig.7 Estimation performance curve of each algorithm under τ=2Tc 图8 时延τ=98Tc各算法的估计性能曲线Fig.8 Estimation performance curve of each algorithm under τ=98Tc 由图7和图8可以看出,当时延τ=2Tc和τ=98Tc时,EVD、SVD和DPASTd算法由于最大特征向量和次大特征向量存在酉模糊导致算法估计性能差,即使在信噪比较高的情况下也无法实现完全正确估计,其中DPASTd算法的效果最差,SVD算法在信噪比为-2 dB以上能够达到正确估计。而本文算法有效消除了酉模糊,优于其他算法,在时延接近零和接近一周期PN序列末端时具有良好的估计性能,即使在-12 dB下也能达到完全正确估计。 仿真评估了各算法在SNR=-10 dB,不同时延下的评估性能曲线,每一个时延使用300次蒙特卡洛仿真,其他条件与实验1相同。其中d=τ/Tc,图9(a)和(b)分别是d为1~10和d为90~99的结果。 图9 各算法在不同时延下的估计性能曲线Fig.9 Estimation performance curve of each algorithmunder different time delays 由图可以看出,EVD、SVD、DPASTd算法在时延越接近一周期伪码序列的始端或者末端时估计性能越差,这是由于此时最大特征向量与次大特征向量接近而存在酉模糊造成的。而本文算法克服了这一问题,在时延接近伪码序列的始端或末端时几乎都能做到完全正确估计,性能总是优于其他算法。 本文方法首先按照2倍扩频码周期为间隔、50%的重叠率进行分段,对矩阵进行奇异值分解,利用矩阵线性变换消除最大左奇异向量和次大左奇异向量之间的模糊,然后利用二者的重叠特性判断时延大概位置,得到去模糊的最大左奇异向量,再利用最大1范数求得具体时延和PN序列。实验证明,本算法具有性能稳定且抗干扰能力强的优点,解决了最大特征向量与次大特征向量接近时的酉模糊问题。
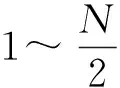

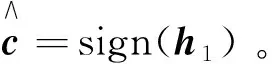
3 仿真实验结果
3.1 实验1




3.2 实验2

3.3 实验3

3.4 实验4
4 结束语
