基于故障树-贝叶斯-蝴蝶结分析的复合事故风险模型研究*

周浩东 姚锡文 许开立 徐晓虎 孙恩吉

(1.东北大学资源与土木工程学院 沈阳 110819； 2.中国安全生产科学研究院 北京 100012)

0 引言

在钢厂连续铸钢生产铸坯的过程中，连铸机浇注漏钢是连铸操作中极其危险的事故，可能造成浇注中断、烧坏设备，严重时甚至造成人员伤亡。韩敬洁等[1]统计发现，连铸各类操作事故中，漏钢事故发生几率最高，占总事故的61%，如图1所示。

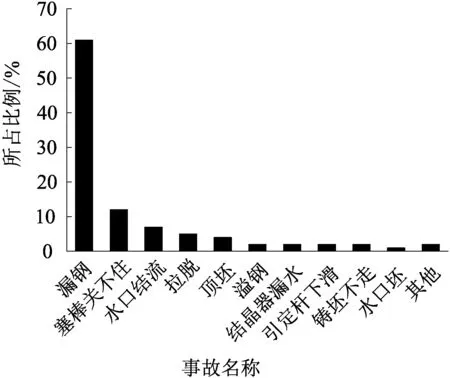
图1 连铸操作事故分布

在连铸漏钢中，根据其表现形式，可以分为粘结性漏钢、裂纹漏钢(包括角裂、纵裂、横裂)、夹渣漏钢、悬挂漏钢、起步漏钢、剪切漏钢等[1]。其中粘结漏钢约占其漏钢事故中的50%～70%，甚至更高。按照其发生概率绘制排列图如图2。

图2 漏钢事故分类分布

但是现阶段尚未从事故发生的角度分析粘结漏钢和其导致事故的后果，以及尚未根据其事故致因和事故后果提出相对应的有效措施。卜全民等[2]分析了故障树的优缺点，指出故障树具有因果关系清晰等优点，但其不能由结果逆向推理原因发生概率；周建方等[3]将事件树和故障树与贝叶斯网络进行了对比分析，指明了贝叶斯网络形式统一，易于统一处理，同时贝叶斯网络在计算方面，问题数量的增加与计算规模呈线性增长，而故障树等其他模型，计算规模大，不利于分析新发生的情况；李俭川等[4]提出了贝叶斯网络在故障诊断中的应用，指明了贝叶斯网络在不确定性和复杂关联性问题中应用的关键及优势；SHENOY P P等[5]将贝叶斯用于化学基础设施的多米诺效应风险分析；MISURI A等[6]将贝叶斯网络应用于关键设施的安全管理中，从而证实了BN网络在结合不同类型信息和参数之间相互影响中具有有效作用；VALDÉS A等[7]将贝叶斯推理用于预测飞机安全事故和风险；ZHANG L B等[8]将贝叶斯用于海上压力钻井动态风险评估。而目前钢铁行业事故复杂，单一的安全评价方法缺乏有效的防治措施，无法降低其危险性，对企业实际生产指导作用有限。

本文通过结合贝叶斯分析与Bow-tie分析，提出了一种故障树-贝叶斯-蝴蝶结复合模型，该模型首先运用故障树，清晰地表达出引起粘结漏钢的基本事件，然后运用贝叶斯网络，分析其基本事件重要度，最后，在贝叶斯网络分析出的基本事件的基础上，运用Bow-tie模型，提出预防该事故发生的措施以及防止事故造成人员伤害的应急保护措施。运用该模型对事故进行分析，不但可以找出引起粘结漏钢的基本事件并将其量化，使其在事故预防中更加具有针对性，而且对概率较大的事件提出预防措施，降低其危险性。该模型在粘结漏钢事故的应用，进一步证实了该模型的可行性。

1 故障树-贝叶斯-蝴蝶结复合模型

故障树虽然可以清晰地表明事故的起因、经过和结果，但是不利于计算和统一处理。在故障树中，我们计算出的结构重要度，在实际生产中并不具有指导作用，其基本事件的重要度不具有代表性，容易造成工作缺乏重点。同时故障树也无法指明事故可能带来的伤害类型，不能直观地提出引起故障的基本事件的改进措施和避免伤害的预防措施。若仅使用贝叶斯网络，虽然在计算方面有了一定的优势，但没有说明故障可能引起哪些伤害，以及没有明确指出相应的改进措施和预防措施。而Bow-tie模型可以将故障树和事件树相结合，同时分析了故障的起因和可能导致的伤害。基于此，本文提出了故障树-贝叶斯-蝴蝶结复合模型。该模型可以定量确定基本事件的危害性重要度，并对其危害性较高的事件分析，形象直观地指出故障可能带来的伤害，并提出预防和改进措施，为实际生产提供指导。

该模型具体方法和步骤如图3所示。首先对故障分析，找出引起故障的中间事件和基本事件，画出其故障树。之后利用故障树的直观性，将其转化为贝叶斯网络，从而可以利用贝叶斯网络强大的计算能力，计算其基本事件的后验概率，进一步可以计算得出基本事件的危害性重要度；最后对其危害性重要度进行分类，找出危害性较大的事件，利用Bow-tie模型分析，不但可以指明引起该事件的原因和该事件可能导致的各种事故类型，而且可以依照各类事件和后果，提出相对应的措施，从而更有效地指导现场安全管理和检查。

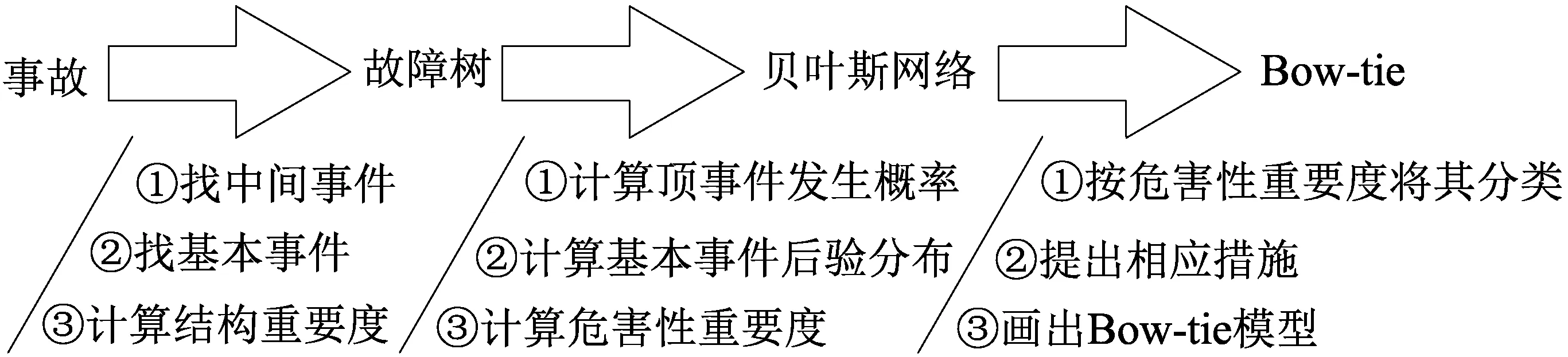
图3 故障树-贝叶斯-蝴蝶结复合模型思路导图

2 复合风险分析模型的应用实例

2.1 粘结漏钢事故故障树

2.1.1 绘制故障树

在炼钢厂中，漏钢是严重的生产事故。在连铸漏钢事故中，粘结漏钢事故比例占全部漏钢事故的一半以上。因此在连续铸钢过程中，应当避免粘结。本文围绕粘结漏钢事故，通过查阅相关文献，总结归纳出引起粘结漏钢的15个基本事件，并将其分为4类，分别为工艺操作不当、结晶器状态异常、钢水不符合标准和保护渣异常。围绕这4类中间事件，绘制故障树如图4，并分析该故障树的最小割集和最小径集以及其基本事件的结构重要度，其中各事件符号含义如表1所示。

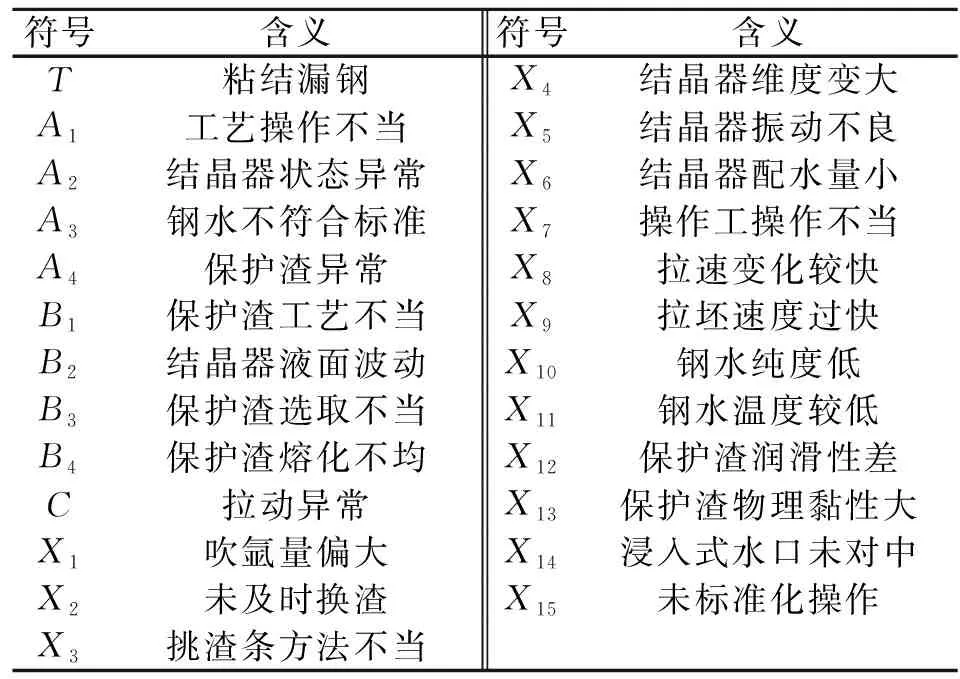
表1 故障树中事件符号及其含义

2.1.2 结构重要度分析

结构重要度从定性的角度，可以明了地反映出各个基本事件对顶事件的重要程度，从而为提出事故预防措施作为参考。

首先，求出故障树最小割集。最小割集中所有的事件发生就会导致顶事件发生，表示了系统的危险性。因为该故障树中或门较多，所以该顶事件最小割集所包含的基本事件较少，事故更容易发生。

该故障树包含13个最小割集，有：{X1}，{X10}，{X11}，{X12}，{X13}，{X14，X15}，{X2}，{X3}，{X4}，{X5}，{X6}，{X7，X8}，{X7，X9}。

根据最小割集，利用式(1)可以确定基本事件的结构重要度，如表2所示。结果从定性的角度，反映了每个基本事件对顶事件发生的影响的相对重要性。

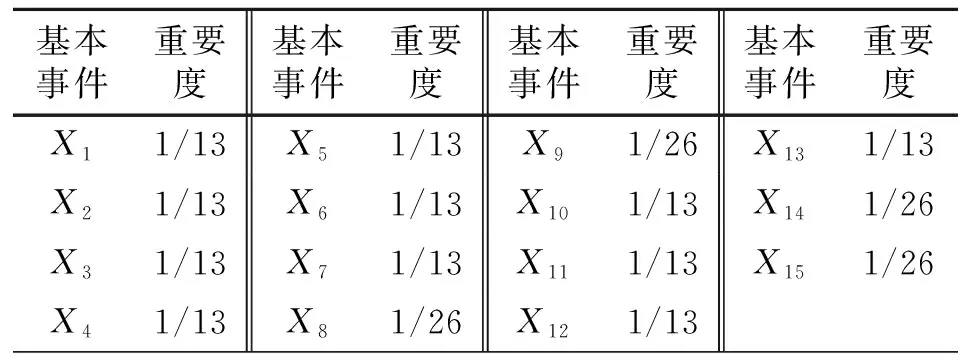
表2 基本事件结构重要度

(1)

式中，n表示最小割集合数量；m表示包含第i个基本事件的最小割集合数量；Rj表示包含第i个基本事件的第j个最小割集合中基本事件数量。

通过以上分析，可以看出单纯的故障树定性分析并不能看出基本事件的对顶事件重要性，不利于企业对事故进行有针对性的预防工作。因此，我们在故障树的基础上，进一步引入贝叶斯，利用其后验分布，从而更加准确地得出导致事故发生的基本事件之间的相对重要性。

2.2贝叶斯网络分析

贝叶斯网络是基于概率推理的数学模型[9]，通过利用一些已知的变量的信息来计算未知变量的概率信息。其数学理论基础为贝叶斯公式：

(2)

式中，P(A|B)是后验概率，P(B|A)是似然概率，P(A)是先验概率，P(B)是标准化常量。

贝叶斯网络具备不确定性推理能力，既可以向前推理，得出顶事件的发生概率，也可以向后推理，在确定顶事件发生的基础上，得出各个基本事件所占比重。因此，运用贝叶斯网络分析粘结漏钢，不仅可以得出其发生概率，而且可以定量地比较各个基本事件对顶事件的影响程度。

2.2.1 绘制贝叶斯网络图

因贝叶斯网络计算复杂，本文利用GeNIe软件，根据粘结漏钢故障树，绘制相对应的贝叶斯网络图，其中故障树中的基本事件对应贝叶斯网络中的根节点，中间事件对应非根节点，用箭头将根节点与非根节点连接并输入其逻辑关系，绘制如图5。通过对钢厂历年粘结漏钢事故原因的统计分析，得出其基本事件的概率分布，如表3。根据贝叶斯网络，计算得出粘结漏钢事故发生概率为0.022 8。

图5 贝叶斯网络

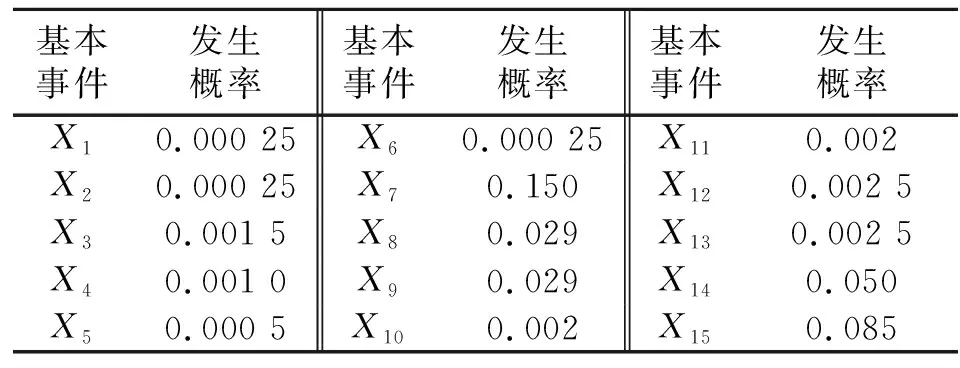
表3 各基本事件的发生概率

2.2.2 网络概率分析

利用贝叶斯网络，通过假设顶事件已经发生，可以逆向求得各个基本事件的发生概率，从而逆向推断出各基本事件的重要性。并考察各个基本事件发生与否对顶事件发生的影响，见表4。

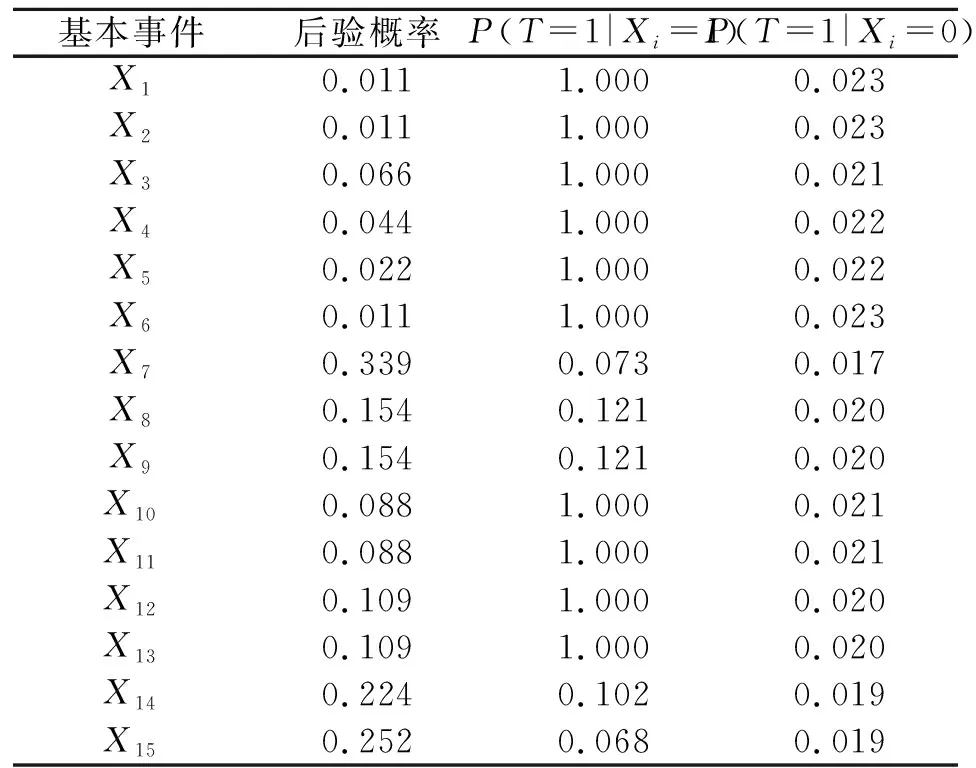
表4 基本事件的后验概率及其对顶事件的影响

通过分析各基本事件的后验概率P(T=1|Xi=1)，可以得出在炼钢中，粘结漏钢极易发生，X1，X2，X3，X4，X5，X6，X10，X11，X12，X13中任何一个发生，都会引起粘结漏钢的发生；通过对后验概率P(T=1|Xi=0)的分析，可以得出，X7，X8，X9，X12，X13，X14，X15中的基本事件对粘结漏钢总的发生概率影响较大。综上分析，可以得出X1，X2，X3，X4，X5，X6，X10，X11，X12，X13虽然可以直接引起粘结漏钢的发生，但是其发生概率较小，不发生的条件下，对顶事件的总发生概率影响微弱。而X7，X8，X9，X12，X13，X14，X15由于其发生频率较高，且其中有与门连接，若能够保证其中的基本事件不发生，可以显著降低事故的发生频率。通过假设X7，X8，X9，X12，X13，X14，X15都不发生，顶事件发生概率为0.007 73，较之前概率降低了3倍。

2.2.3 基本事件重要度分析

根据基本事件后验概率的大小及其对顶事件的影响程度，我们可以综合性地得出基本事件重要度。本文利用危害性重要度[10]：

(3)

式中，P(Outcome=j|xi=1)表示该基本事件发生条件下顶事件发生概率；P(Outcome=j|xi=0)表示该基本事件不发生条件下顶事件发生概率；P(Outcome=j)表示顶事件发生概率。危害性重要度是将基本事件对顶事件的影响以及基本事件本身发生概率结合起来考虑，具有很强的综合性。

通过利用式(3)分析计算，将引起顶事件的基本事件按照其危害性重要度分为3类，第一类为：{X12，X13，X14，X15}；第二类为：{X7，X8，X9}；第三类为：{其他基本事件}。

因此，本文重点研究X7，X8，X9，X12，X13，X14，X15的产生原因及其影响度。可以看出引起粘结漏钢的主要原因有：①由于浸入式水口未对中或未标准化操作从而引起的保护渣熔化不均和保护渣选取不当，都存在引起保护渣异常的可能性；②操作者操作不当，同时拉动异常，引起了液面波动，从而导致粘结漏钢。

2.3 Bow-tie分析

从贝叶斯后验概率可以看出，其后验概率大于0.1的有第一类基本事件和第二类基本事件，中间事件为液面波动和保护渣异常。其中保护渣异常所占比重略大。因此，我们利用Bow-tie分析法分析保护渣异常，分析了引起保护渣异常的原因和保护渣异常可能导致的各种伤害事故，从而可以精准地提出各种原因对应的安全措施，降低其风险设置事故后果的屏障。

Bow-tie模型是一种综合性的风险分析方法，其不但可以通过结合故障树模型，精确地表达出事故发生的途径，而且可以表达出事故可能导致的各种后果。结合事故发生途径和可能导致的后果，可以逐个提出措施和设置屏障。Bow-tie模型所提出的措施，一方面可以降低事故发生的可能性，另一方面可以减小事故带来的损失，阻止事故进一步扩大。因此，本文通过贝叶斯分析，找出发生概率较高的事件，并运用该模型，降低事故风险，减少事故损失。通过对保护渣异常原因的分析，提出了17条建议，见图6。

图6 Bow-tie分析

通过图中模型，可以清晰地看出引起粘结漏钢的4种原因和可能导致的3类事故，从而有针对性地提出17项安全措施，分别为10项防止事故发生的预防措施和7项防止造成人员伤害的人员应急保护措施。从而使粘结漏钢故障发生率进一步降低，有效地指导实际生产和应用。

3 结论

(1)提出了故障树-贝叶斯-蝴蝶结复合模型，从而解决了故障树模型中的结果无法逆向推理等问题，同时避免了单一模型的片面性，从事故原因、基本事件危害性重要度和预防措施三个方面全面地描述了一个故障及其预防措施。

(2)该模型集成故障树、贝叶斯和Bow-tie模型，同时分析了故障的起因和可能导致的伤害，并提出了相应的预防措施，从根本上避免了伤害事故的发生。

(3)引入危害性重要度，可综合考虑各个基本事件的重要度。发现在粘结漏钢事故中，导致液面波动和保护渣异常的基本事件占比较大，在防止粘结漏钢事故中，应注重这两个中间事件所对应的基本事件。

(4)将该模型成功应用于粘结漏钢故障中，验证了其可操作性。利用贝叶斯网络确定该故障的基本事件危害性重要度，并运用Bow-tie模型，以保护渣异常为事故分析，结合导致保护渣的4类基本事件以及可能造成了3种事故后果，提出了预防该事故发生的10项措施以及防止事故造成人员伤害的7项人员应急保护措施，从而方便在实际生产中应用，以实现降低事故发生概率及减小事故损失的目的。