收缩徐变对矮塔斜拉桥主梁挠度的影响
2020-08-29郁光耀
郁光耀
中铁十一局集团第五工程有限公司
1 引言
混凝土收缩、徐变效应与应力情况与混凝土龄期有着密切的关系,在研究混凝土收缩、徐变的模型时,由于影响因素多,机理复杂,没有选定的计算模型或者计算参数。本文针对长湾澧水矮塔斜拉桥,通过理论计算的分析,对矮塔不等跨斜拉桥不同时间段对梁体挠度的影响进行分析与计算,进而指导现场施工。
2 混凝土收缩徐变计算理论
2.1 收缩计算理论
在应力变化条件下,从加载时龄期t0到观察时刻t,所产生的应变总和为:
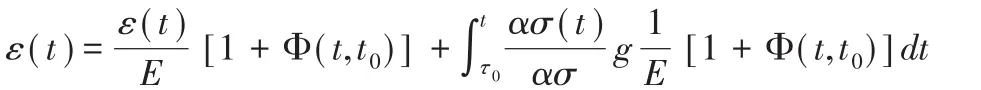
根据我国学者金成棣提出的应力松弛规律:
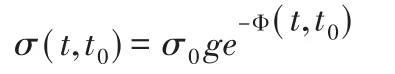
再引入折算系数:
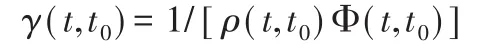
上式简化为:
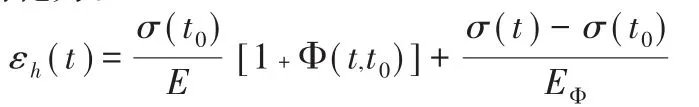
式中:
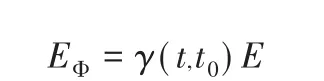
上式即为在变化应力条件下,t时刻结构内混凝土徐变的总应变计算公式。应用虚功原理求得结构因混凝土徐变的总变形计算公式:
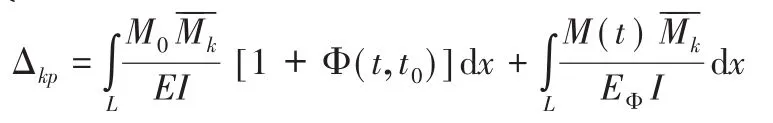
式中:
M(t)——结构徐变次内力,计算式前项为结构在加载龄期t0时初始力引起的总变形(弹性变形与徐变变形之和),后项是结构徐变次内力引起的总变形。
2.2 徐变计算理论
桥梁结构的收缩是长期变形与结构应力无较大的影响,自t0至t时的收缩应变值εcs(t,t0):
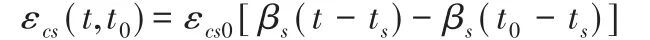
式中名义收缩系数εcs0根据公路钢筋混凝土及预应力混凝土桥涵设计规范。
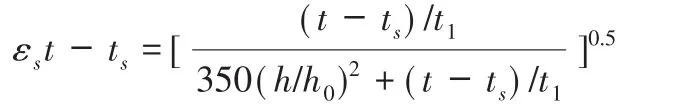
当采用手算方法时,应对结构构件简化,结构的简化与桥梁实体往往会存在一定的差别,这些差别会引起计算结果的差异,从而导致手算结果出现较大的误差,在实际计算中更多地采用有限元仿真计算的方法,有限元计算结果更接近于实际情况。
2.3 收缩徐变有限元分析方法
有限元逐步分析法是将构件在收缩徐变的全过程划分为若干相互连接的小过程,根据应变相容条件求出该过程的应力或内力的变化,从而得出该过程结束时或下一过程开始时的应力应变状态,并开始进行下个过程的计算。对分段施工的混凝土从ti时刻到tn时刻的由收缩徐变引起的总应变:

假定截面Sj 在时刻εcs ( t,t0)产生,在εcs ( t,t0)内徐变增量为εcs ( t,t0)内力增量为εcs ( t,t0)最后εcs ( t,t0)的总位移和总内力为:
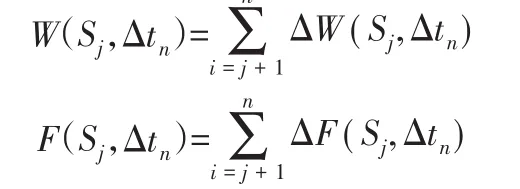
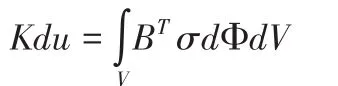
3 计算分析
长湾澧水大桥主桥斜拉桥共计有44个施工节段,梁体1~44号段采用悬臂浇筑的施工方法,墩顶12.0m为0号梁段,(1)~(14)号梁段长3.0m,(15)~(40)号梁段长3.5m,(41)~(44)号梁段长5.0m,(41’)~(44’)号梁段长3.0m,(45)(45’)号梁段为合拢段,梁段长2.0m,小里程和大里程现浇梁段长分别为11.75m和5.75m。

图1 桥梁布置图
用有限元软件对桥梁结构进行模拟分析,全桥共分为263个节点345个单元。
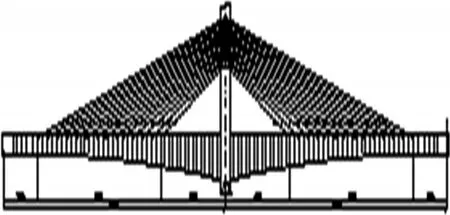
图2 桥梁计算模型
通过分析梁体运营荷载和后期的收缩徐变对梁体的影响,图3和图4是二期恒载后10年每年收缩与徐变对主梁挠度影响情况,从图3和图4可以看出:
(1)在10年内收缩与徐变引起主梁的挠度量都在第1年发生最大,其中收缩挠度量第1年占10年的28%,徐变挠度量第1年占10年的49%。
(2)成桥运营第2年和第3年间收缩引起的挠度将占阶段总挠度的26%,徐变引起的挠度将占阶段总挠度的32%。
(3)收缩徐变对主梁挠度的影响在10年内影响是相当巨大的,且主要发生在前3年,3年之后逐渐变小趋于稳定。
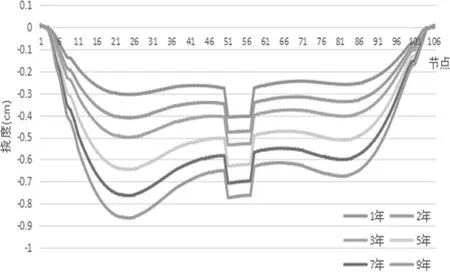
图3 前10年每年收缩对挠度的影响情况
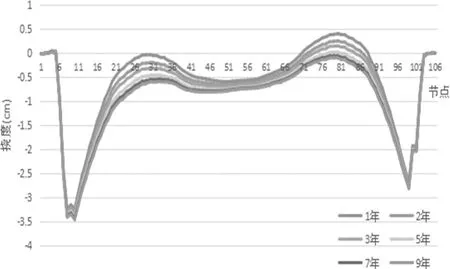
图4 前10年每年徐变对主梁挠度情况
图5和图6为主梁在10年内、20年内、100年内收缩徐变对主梁挠度的影响情况,从图3和图4可以看出:收缩对主梁挠度的影响随时间减弱的程度比徐变对主梁挠度影响要小,100年后收缩对主梁挠度约为10年后的1倍,这说明前面10年与后面90的收缩对主梁挠度影响相当;10年后徐变对主梁的挠度影响变化很小,徐变对主梁挠度的影响主要发生在前10年,那么在设置施工预拱度时考虑10年的收缩徐变即可。
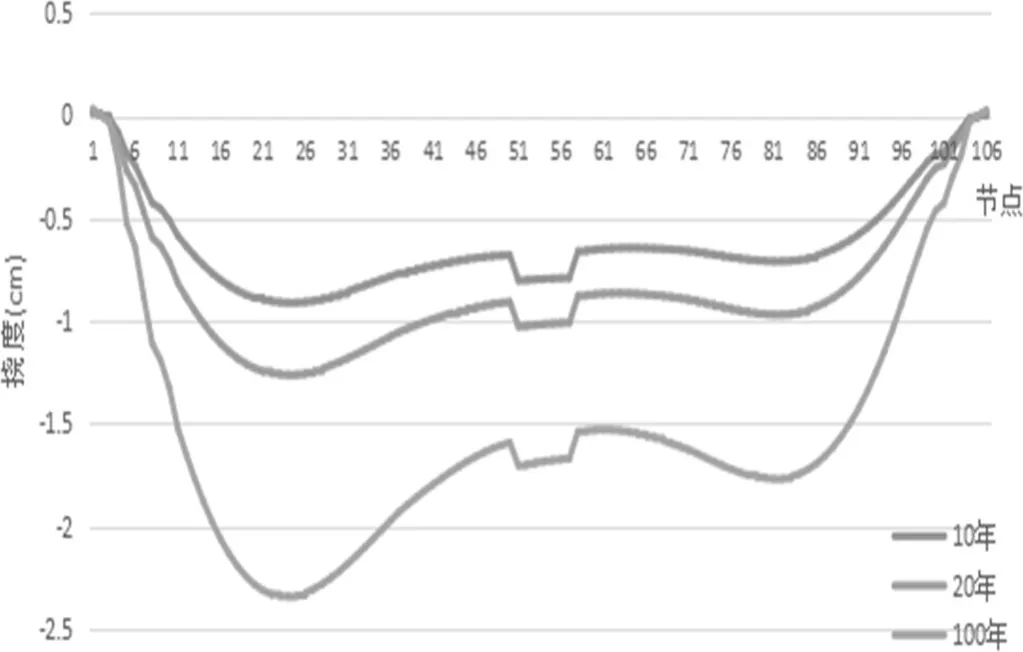
图5 10年、20年、100年收缩对主梁挠度影响情况
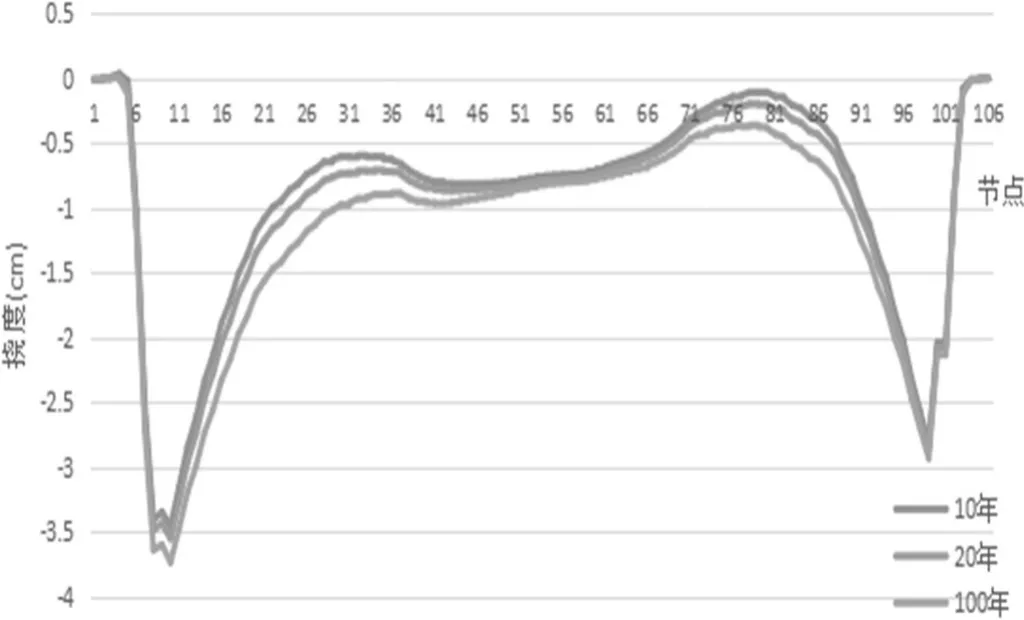
图6 10年、20年、100年徐变对主梁挠度影响情况
4 减少收缩徐变对主梁挠度影响的方法
目前节段梁体的收缩徐变与梁体挠度的影响的分析计算主要是通过一些假设和经验的数据上,在实际施工中为了减少梁体的收缩徐变的影响,主要通过调整相应的施工方法和步骤,主要是方法是:
(1)优化预应力设置;(2)调整合拢顺序;(3)调整合拢方法;(4)合拢段配重;(5)根据计算的理论值调整预拱度;(6)合拢时施加顶推力;(7)合拢段使用膨胀混凝土;(8)调整混凝土的配合比;(9)梁体预留备用预应力束。
5 结语
通过对矮塔斜拉桥的收缩徐变在不同时间段主梁挠度与收缩徐变的关系运用有限元及通过一些假设和经验的数据,为实际施工中减少梁体的收缩徐变的影响,
