用于地面模拟平台测试光学相机的设计

荆 丹，杨 振，谷 岩*，林洁琼，周晓勤

(1.长春工业大学机电工程学院，长春 130000；2.吉林大学机械与航空航天工程学院，长春 130000)

成像设备研制的过程中，对于非球面镜片的引入是一项新兴的技术，在航天侦察、空间卫星、地面检测等各领域实施应用，例如中国科学院长春光学精密机械与物理研究所杜康等人应用了非球面研制出大相对孔径微型星敏感器镜头，仅用 5 片镜片，即可实现焦距 25 mm，相对孔径 1/1.3，17°全视场角[1]。引入非球面可以增加更多可调整镜面参数从而在减少镜片数量的同时达到较高的成像质量，中国工程物理研究院激光聚变研究中心研究人员利用非球面镜研制的光学结构可用于聚焦大功率超短脉冲激光[2]。研究人员通过对非球面检测方法进行改进，非球面制造及测量的精度已经达到了很高的水准[3-4]。在光电侦察中，使用球面需要21片透镜，而非球面只需要5片透镜；镜片制造周期从2个月减少到10 d；质量从5 kg减少到1 kg[5]。利用非球面镜面可以使像差极大地改善；此外，通过修改表面的曲率，使近轴光线的交点与离轴光点重合，对于增加入射光线的高度和视场角有很大的作用[6-7]。研究结果表明，非球面镜片应用在成像光学系统中有着极大的优越性。相机应用于航空相机的地面模拟检测设备中，具有体积小、重量轻、成像质量高等特点，对于精密的地面模拟设备的调试更为精确，为后续研制轻型成像设备提供参考。通过光学仿真设计软件ZEMAX优化光学系统，并通过添加非球面提高系统的成像质量，减轻相机的重量，投入生产制造，最终对加工产出的非球面面形进行检测，对加工出的镜片进行组装，通过图像采集验证成像质量观察其成像效果计算最佳物距。

1 光学系统设计

1.1 初始光学数值的计算

首先计算相机的入瞳直径D，其计算公式如式(1)所示:

(1)

式(1)中：D为入瞳直径；f′为镜头焦距，取80 mm，F为镜头F数，F=8，求得入瞳直径D为10 mm。

根据视场，可以获得检测器的有效区域。

(2)

式(2)中：ω为半视场角；2y′为CCD(charge coupled device)传感器的对角线尺寸，则可以计算出相机镜头的CCD传感器的接收面对角线尺寸为2y′= 39.892 mm。

设计的相机用于地面模拟平台成像仿真实验，相机成像系统预期的参数如表1所示。

表1 预期光学系统参数

1.2 初始结构的选取和像差的校正

1.2.1 初始结构的选取

初始光学结构的挑选是光学系统总体设计的前提。首先要满足镜头设计基本的要求在基本结构满足的情况下再进行初级像差的校正[8]，选择合适的初始结构可以大大缩短设计周期。通过比较焦距，光圈和视场来从现有光学系统中选择近似光学系统。选择双高斯光学结构作为初始结构，如图1所示。该光学系统共有25个设计参数，包括12个表面曲率，6个透镜厚度，5个空气间距和后焦距。

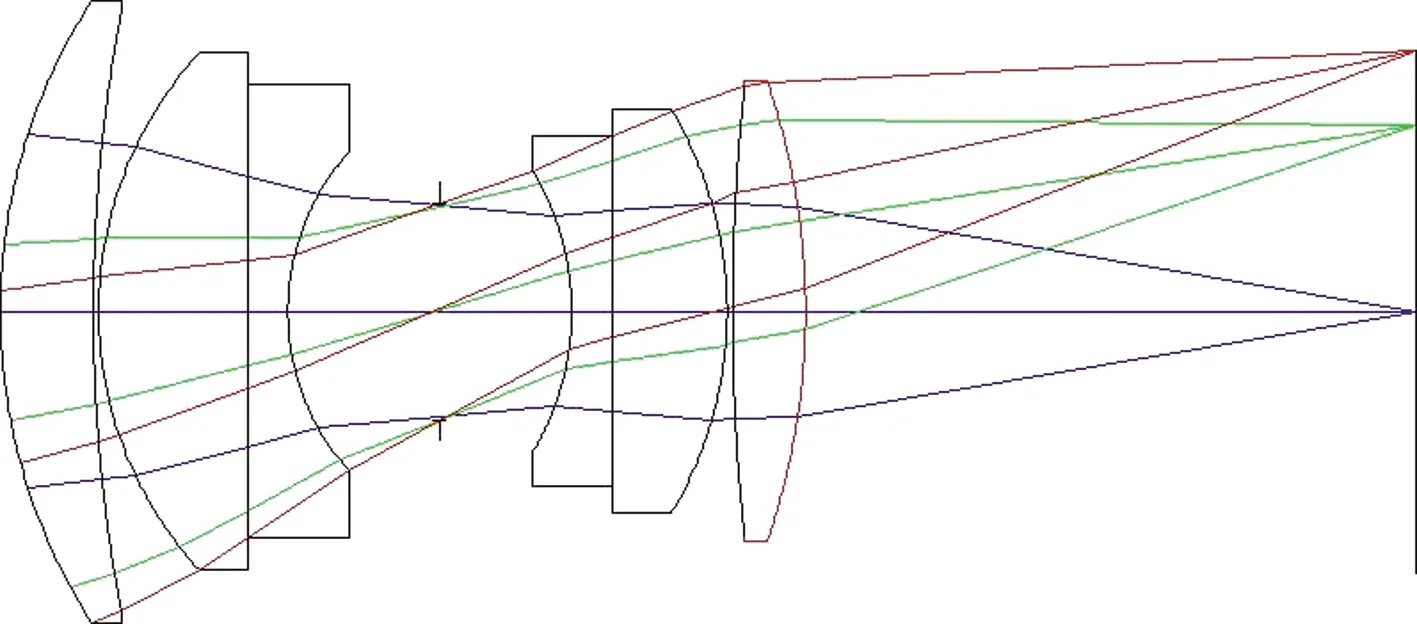
图1 初始光学结构

1.2.2 像差的校正

从ZEMAX镜头设计软件自动生成光学系统数据，初始镜组的设计数据如表2所示。

表2 初始数据

对于具有固定物距的透镜，提高设计效率是必要的[9]。用ZEMAX软件模拟光学系统，发现系统中存在严重影响成像质量的像差。因此，应优化光学系统的参数。通过ZEMAX中的默认评价函数优化光学系统。附加的辅助操作数用于平衡特定的像差。默认优值函数的重要性在于，当从特定图像平面给出物体的光时，将计算像差。默认选择是RMS+Spot Radius+Centroid，然后添加少量自定义优化目标。表3为优化中使用的优化函数。

表3 优化操作数

以下是对优化后光学系统的分析。结果表明仍然存在不符合初始目标的像差。从图2可以看出，MTF(modulation transfer function)的值远小于0.3@91 lp/mm。图3为初步优化后的弥散斑图，其中均方根半径的最大值为569.915 μm，几何半径的最大值为1 000.44 μm，远远大于艾里斑半径。这些结果意味着光学系统无法满足成像要求。因此应该更深入地优化系统。

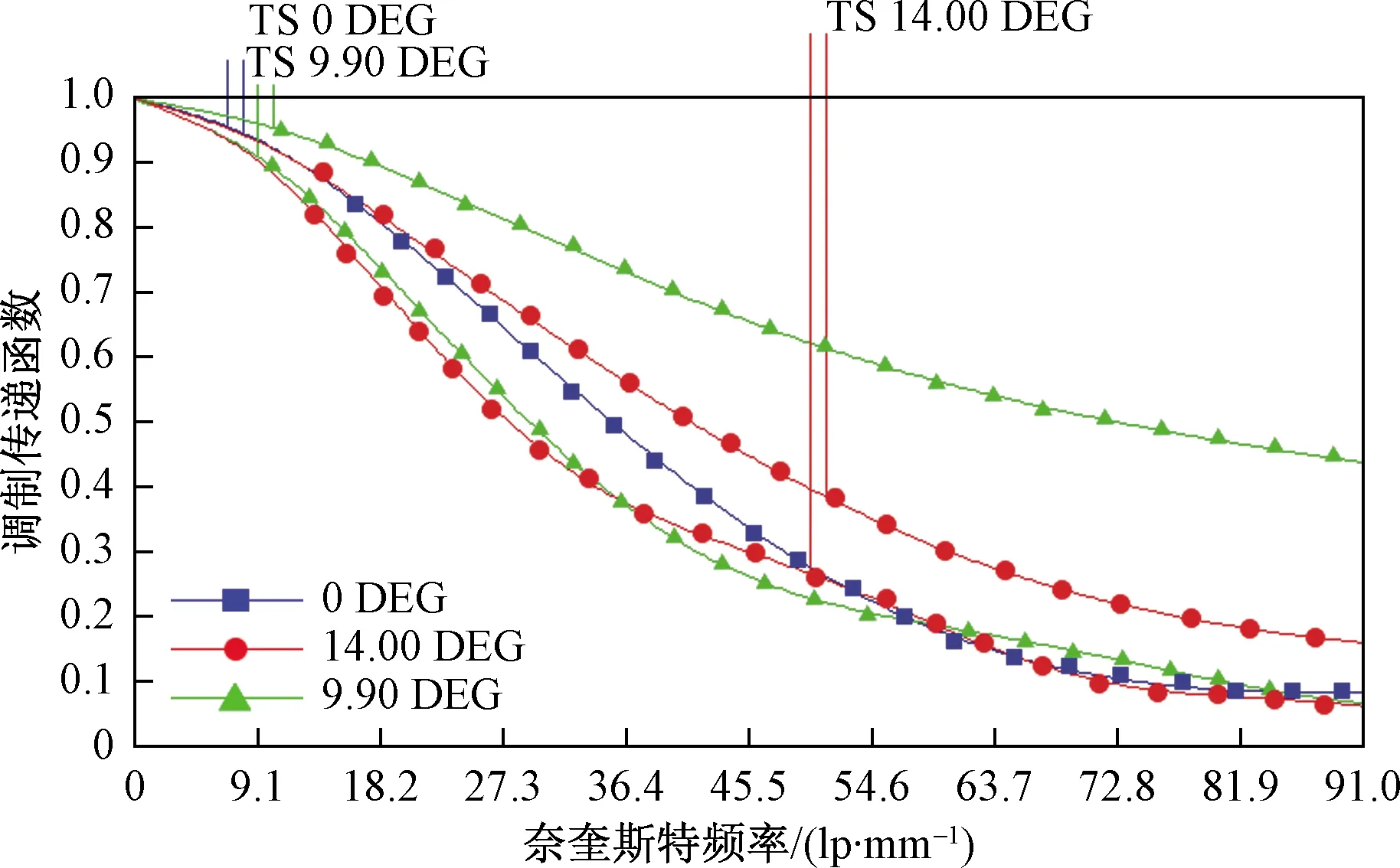
DEG表示视场角

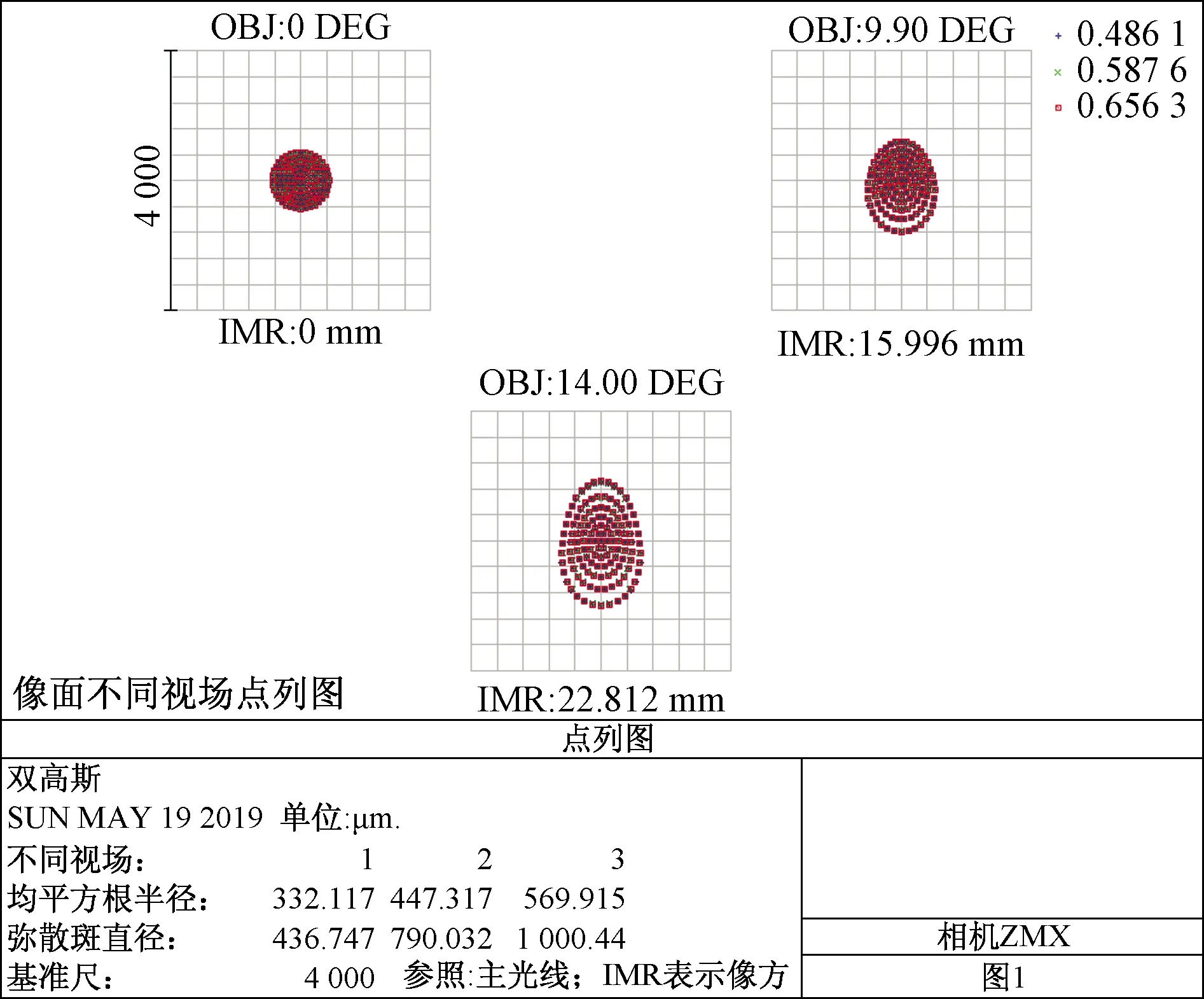
OBJ表示物面

1.3 利用非球面提高图像质量

非球面可以用于校正像差，同时可以减轻镜头的重量[10]。图4分别是使用球面表面和非球面表面校正球面像差的效果。图4(a)球面相较于图4(b)中的非球面，球面可优化因素较少，非球面表面在校正球面像差方面更具有优势。

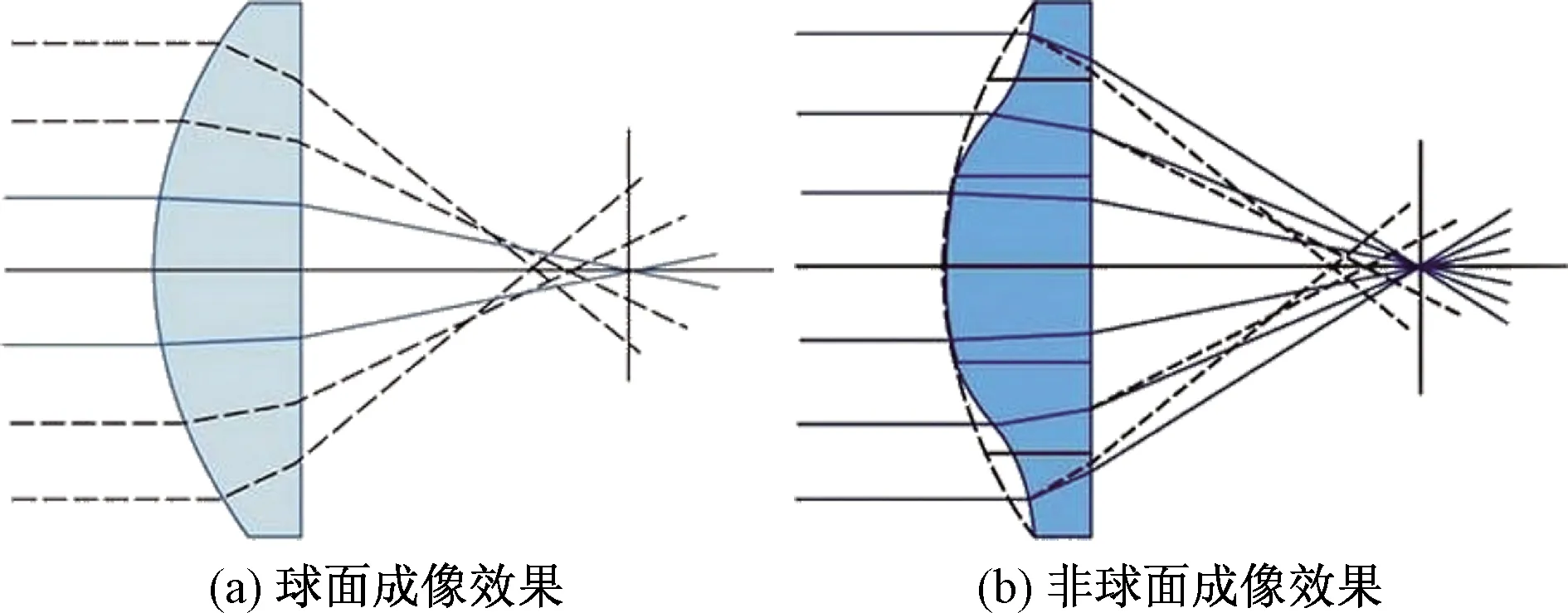
图4 球面成像与非球面成像效果

利用已知的公式，一般的非球面可以表示为

(3)

式(3)中：c为二次球面系数；B、C为高次非球面系数；r为曲率半径。球面公式如式(4)所示：

(4)

通过式(3)、式(4)可以在仅考虑初级像差时推导出式(5)：

(5)

式(5)中：n′和n分别为光入射、出射折射率；ΔB为变形系数；ΔS为初级像差，用于解释球面和非球面的差异。初级像差理论主要像差为

ΔSⅠ=(n′-n)ΔBc3r4

(6)

(7)

(8)

ΔSⅣ=0

(9)

ΔCⅠ=0

(10)

ΔCⅡ=0

(11)

优化的光学系统中存在高阶像差。为了使其具有预期的成像性能，有必要合理地使用非球面来校正其初级和高阶像差。散光和球面像差明显增加。因此，选择具有较大ASP的表面作为非球面。计算后，选择光学系统的第4面作为非球面。所研究的非球面是偶数阶非球面，用式(12)[12]描述。

(12)

表4 高次非球面系数

在ZEMAX软件的仿真中，建立了一个非球面光学系统，如图5所示。每个表面的半径，厚度和直径如表5所示。然后通过使用先前的操作数来优化光学系统。

图5 增加了非球面的光线结构

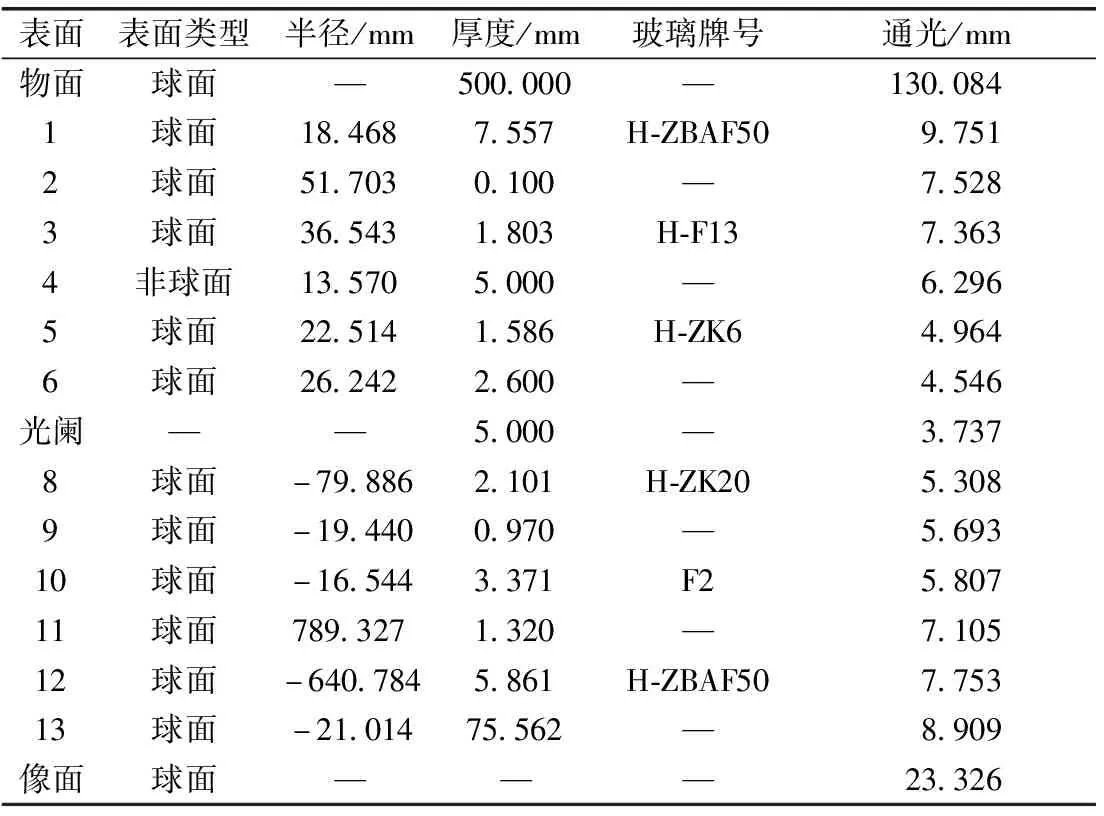
表5 镜组数据

MTF曲线和几何点图分别如图6、图7所示。图6显示所有领域的MTF均大于34%@91 lp/mm。与之前的MTF曲线相比，MTF增加了42%以上。从图7可以看出，艾里斑半径为6.722 μm，最大RMS(root mean square)半径为1.879 μm，最大地理信息定位(GEO)半径为3.955 μm。分析结果表明光学系统可以接近衍射极限。

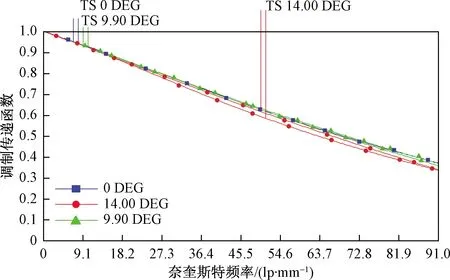
图6 非球面化后的MTF曲线

图7 非球面化后的光学点列图

航空相机光学系统的场曲和畸变如图8所示。相对失真的最大值为0.28%，远小于设计要求。

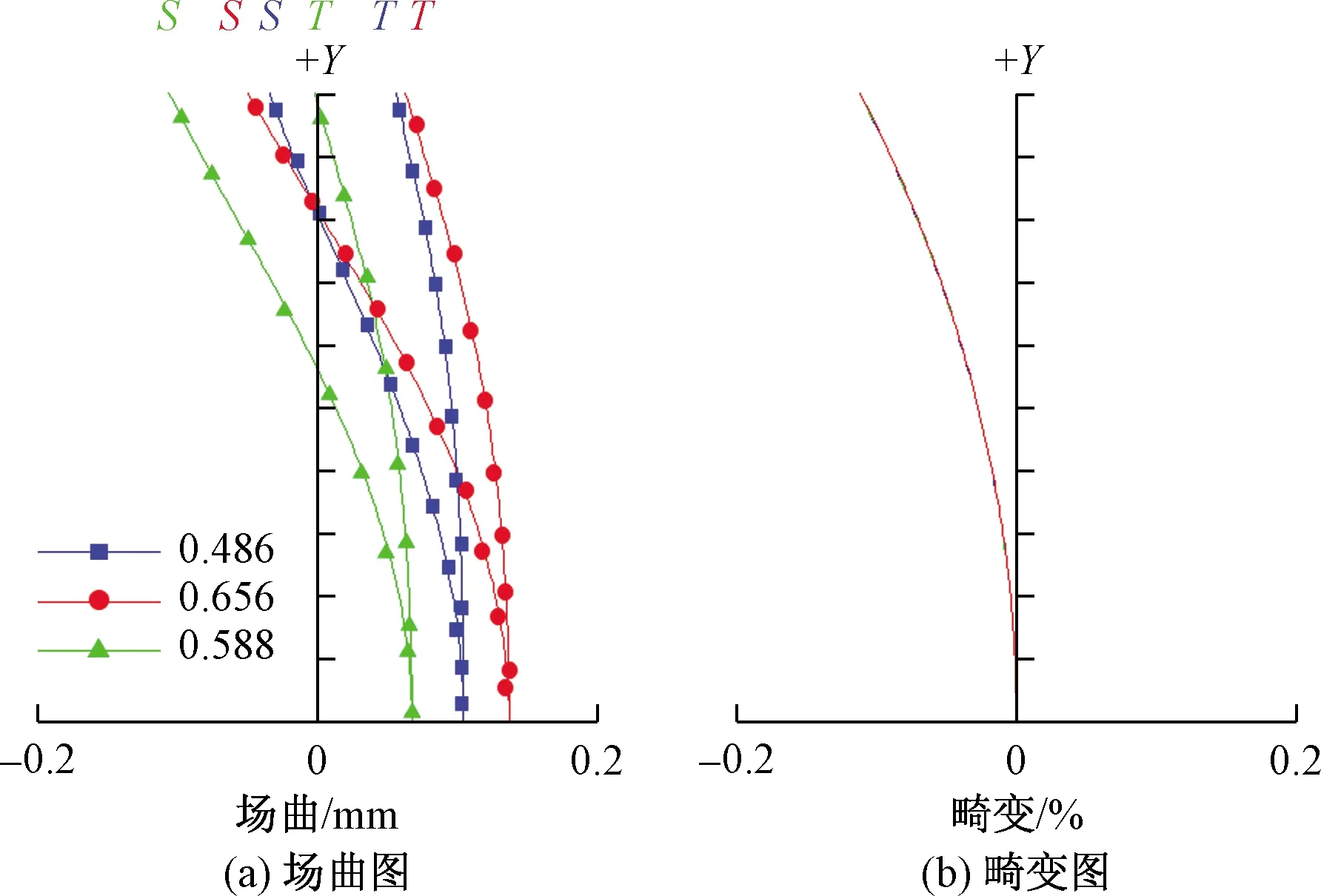
T表示子午方向不同视场角场曲；S表示弧矢方向不同视场角场曲

与以前的光学系统相比，MTF曲线得到显著改善，RMS半径和GEO半径小于艾里斑半径，并且在要求范围内没有失真。

2 非球面镜片检测成像实验检测

2.1 非球面镜片检测

投入加工后产出的镜片实物如图9所示，使用ZYGO(美国翟柯公司)干涉仪对加工后的非球面镜的PV(peak value)、Ra(average roughness)和RMS(root mean square)值进行检测，最终结果如图10所示。最终测得PV为14.422，Ra为2.641，RMS为3.102，均在合理范围之内。

图9 加工完成的非球面镜

图10 ZYGO干涉仪检测图

2.2 成像实验检测

通过分辨率评估图像质量是一种广泛接受的系统性能测量[13]。通过调节转速控制箱调节标准分辨率转筒从而使CCD相机组件获得目标图像,拍摄ISO12233的照片，如图11所示。

图11 相机检测设备

测试相机的成像性能。通过调整镜头与标准分辨率转筒测得相机具有83 mm的焦距，目标转速通过电机的调速装置调为0.24 m/s时，相机扫描成像如图12所示。从图12可以看出，在分辨率图的最小图像中依然可以分辨出黑线，满足相机的成像质量要求。

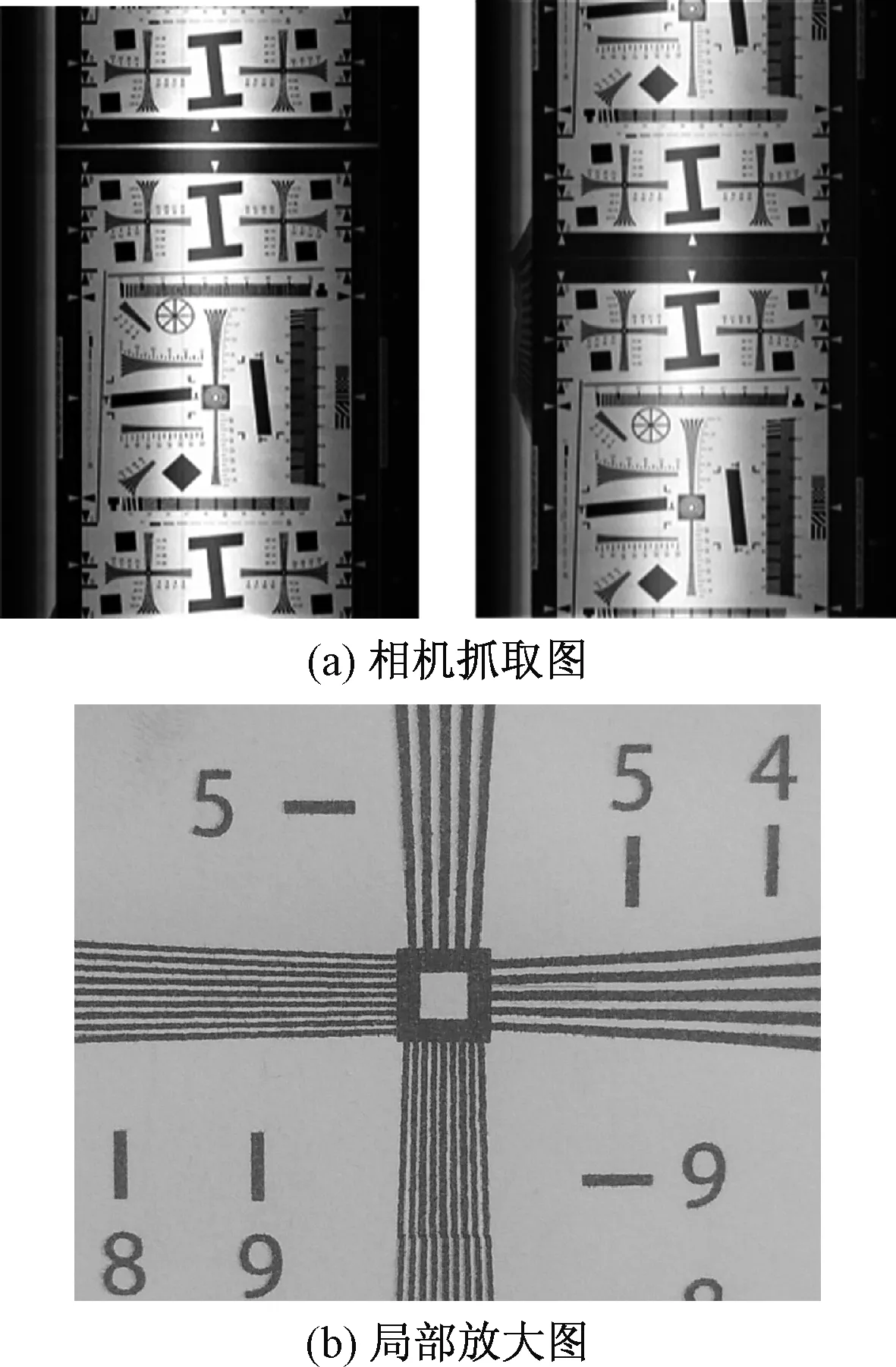
图12 抓取图样及其局部放大图

通过式(13)计算相机的最佳物距：

(13)

式(13)中：l′为图像距离；l为物距；f′为焦距。计算得到的最佳物距为547 mm，从采集图片(图12)的清晰度可以看出，研制出的非球面检测相机具有高分辨率，满足设计要求。

3 结论

对非球面检测相机进行了设计及实测。结果表明，基于非球面的光学系统的性能优于基于球面的光学系统。测试证明相机可以满足设计要求。光学系统优化后，光学系统的MTF优于34%，RMS半径和GEO半径均小于艾里半径，光学系统的失真小于1%。利用ZYGO干涉仪检测非球面镜合格,测试数据显示相机焦距为83 mm，最佳成像距离为547 mm。测试图像显示相机成像效果可以满足要求。