钢纤维混凝土弯曲性能和纤维分布试验研究
2020-08-28刘冠志
赵 健, 廖 霖, 张 帆, 刘冠志, 王 梅
(太原理工大学 矿业工程学院, 山西 太原 030024)
钢纤维混凝土(steel fiber reinforced concrete,SFRC)是一种新型水泥基复合材料,因具有良好的性能而被广泛应用于工业、民用和军事等重大结构[1-2].由于SFRC具有显著的增强和阻裂效应,在一定程度上可以延缓基体自身微裂纹的生长和微空洞的塌陷,从而使其抗拉、抗弯、抗剪强度等较普通混凝土有显著提高,其抗冲击、抗疲劳、裂后韧性和耐久性也有较大改善[3-4].SFRC的力学性能主要取决于分布在基体中的纤维含量和方向[5].随着纤维含量的增加,SFRC破坏截面处的钢纤维数量也在增加[6];纤维分布方向决定了纤维与SFRC破坏截面间的角度,当纤维与破裂面之间的角度为30°~45°时,纤维在基体中的锚固黏结力最大,对混凝土的增韧效果也最明显[7].影响纤维分布方向的因素有很多,例如纤维的形状和含量、混凝土配合比和浇筑方式等[8-9].此外,国外许多规范将纤维分布的方向系数考虑进了混凝土结构设计中.在《Fib model code for concrete structures 2010/International federation for structural concrete(fib)》中,引入纤维方向系数K来表示纤维分布方向对混凝土结构设计强度的影响:当K=1时,认为纤维等方向分布;当K<1和K>1时,则认为纤维沿不利和有利的方向分布.德国混凝土规范《Guideline for steel-fibre-reinforced concrete》中,纤维方向系数Kf被引入到混凝土构件峰后强度的计算中,一般情况下,Kf取为0.5;当纤维与受弯构件的纵向平行时,Kf取为1.0.挪威和瑞典的SFRC设计规范《Forslag til retningslinjer for dimensjonering, utfrelse og kontroll av fiberarmerte betongkonstruksjoner,proposed guidelines for design, execution and control of fibre reinforced concrete structures》、《Design of fibre concrete structures》中,直接将SFRC残余强度与纤维方向系数相关联,并提出了相关计算公式.因此,为了准确衡量SFRC性能,对混凝土中钢纤维分布方向的检测变得尤为重要.对于混凝土中纤维分布方向的检测可以分为破坏性检测和非破坏性检测[10].
破坏性检测主要包括人工统计法[6,11]和图像处理技术[12].
人工统计法是通过统计破坏截面上的纤维根数及其分布,来分析钢纤维的分布方向.这种方法简单、易操作,但是需要花费大量时间和精力.
图像处理技术是对SFRC试件进行切割打磨,并对切片进行拍照处理,通过分析纤维截面形状得到纤维的分布方向.但SFRC试件的切片和抛光步骤繁琐,拍照可能会遗漏部分纤维,导致出现误差.
非破坏性检测主要是利用钢纤维与混凝土材料特性的不同,通过电、磁等手段来检测钢纤维在混凝土中的分布情况,主要有X射线法[13-14]、交流电阻抗光谱法[15]、C型磁铁探针法[16]、电阻率测量法[17]和电感试验法[18-20].
X射线法是利用钢纤维与混凝土之间的密度差异,采用CT成像技术扫描SFRC样品并重构界面X射线吸收密度轮廓图来观察混凝土中的纤维分布.这种方法可以准确直观地测得纤维的分布,但是对试件尺寸有限制,目前仅适用于小试件的实验室研究.
交流电阻抗光谱法(AC-IS)是利用钢纤维与混凝土的导电率差异,通过对SFRC试件施加电压以激发宽范围的交流电信号,测量出不同的输出电流,计算得到钢纤维在混凝土中的分散性和分布特征.但是此方法试验装置价格昂贵,电极和试件间阻抗会影响数据准确性.
C型磁铁探针法是利用钢纤维的导磁性,将绕线C型磁铁作为探针放在SFRC试件表面,通过测量其阻抗变化来快速测量钢纤维的分布.该方法能够快速得到纤维分布信息,可以用于原位测试,但是其使用范围非常有限,仅能测量较薄试件或结构表面的纤维分布.
电阻率测量法利用四探针测量SFRC表面2个垂直方向的电阻率,利用不同位置电阻值的变化来表征纤维分布方向和结团信息.该方法适用于工程中的原位检测,但是由于混凝土龄期、湿度不同会对电阻率产生影响,降低了其准确性.
电感试验法利用电磁感应原理,通过线圈电感值的变化来表征SFRC试件中钢纤维的分布.电感试验不仅可以测量基体中钢纤维的分布方向,还可以估计钢纤维的含量.该方法的缺点是不能用于大尺寸试件和工程原位测试.
本文详细介绍了电感试验的原理、装置和试验方法,并设计了SFRC切口梁三点抗弯试验,结合电感试验分析了不同纤维含量下SFRC的弯曲性能和纤维分布,以便为准确评价SFRC性能提供可靠依据.
1 电感试验
1.1 电感试验原理
电感试验法是以介质电磁性的差异为基础,通过研究交变电磁场随空间分布规律或随时间变化规律,达到勘察目的的无损检测方法.一个绕线材料、匝数、截面形状和通电状态均固定不变的空心通电线圈,其电感值仅与线圈中的介质材料有关,介质材料磁导率越大,则线圈电感值越大.对于SFRC而言,混凝土基质磁导率与真空磁导率为同一数量级,其值近似为1H/m,可认为将其放入磁场后不增加线圈电感;但钢纤维属于铁磁材料,其磁导率为200~400H/m,远大于混凝土基体的磁导率,因此将SFRC放入通电空心线圈中后,线圈电感的增加可认为只是由钢纤维造成的,且钢纤维含量越多,电感增量也就越多.此外,若钢纤维的排列方向平行于磁场线,则电感增量最大;若纤维排列方向垂直于磁场线,则电感增量最小,约为平行排列时的1/9[18].通过分析每个试件三轴电感增量ΔLX、ΔLY、ΔLZ之间的关系,可判断出基体中钢纤维的分布概况.
根据Torrents等[18]和Cavalaro等[19-20]的研究,发现三轴方向的电感增量之和(ΔL)与纤维含量(Cf)存在线性关系,且该关系与钢纤维在混凝土中的分布无关.因此,如果可以提前测得所使用纤维的上述关系曲线,就可以很好地估算混凝土中的纤维含量.纤维含量Cf的计算公式如下:
Cf=ω·∑i=X,Y,ZΔLi=ω·ΔL
(1)
其中比例系数ω为:
(2)
式中:ρ、d分别为钢纤维密度、直径;λ为钢纤维长径比;V为试件体积;k为与施加磁场有关的常数;γ为与钢纤维形状有关的因子,本文取0.05.
通过式(2)可以看出,ω的大小主要与钢纤维的特征和所加磁场有关.因此对于同一种钢纤维,ω可以通过破碎试件后得到的纤维含量和电感增量间的线性回归关系计算得到.
为了研究钢纤维在基体中的分布状况,本文使用纤维方向数(ηi)来评价纤维在某一方向上的贡献,即基体中所有纤维与某方向夹角余弦值的平均值.Cavalaro等[20]根据电磁感应理论得到下式:
ΔLi=k[cos2αi+γ(1-cos2αi)]
(3)
=k(1+2γ)
(4)
式中:αi为纤维与磁场磁感应线方向的夹角.
通过式(3)、(4)可以推导得到纤维方向数ηi的计算式:
(5)
上述公式均是在磁场均匀的假设下得到的.但是由于磁场在线圈中的分布并不均匀,当纤维靠近线圈端部或内壁时,电感值会变小,此时会高估纤维方向数.式(6)、(7)分别为修正后纤维方向数ηi和纤维方向数相对比例Ci的表达式.
(6)
(7)
1.2 电感试验装置
电感试验设备由线圈、底座和数字电桥测试仪组成(见图1).Torrents等[18]在早期制作的线圈,是由直径为0.2mm的绝缘导线非连续地缠绕在立方体壳体上得到的(见图1(a)).立方体壳体尺寸为15cm×17cm×17cm,导线共缠绕2354圈,总长2600mm.但是立方体线圈形成的磁感线并不均匀,在靠近线圈壁和转角处的磁感应强度较线圈中心小,这极大地增加了试验误差;此外,立方体线圈只能测量三轴均对称的立方体试件,这大大限制了装置的使用范围,对于圆柱体取芯试件和其他形状的试件无法测量.
为此,Cavalaro等[20]对电感设备进行了改装,提出了一种可以测量圆柱体和立方体试件的线圈(见图1(b)).改装后的线圈由绝缘铜导线缠绕亚克力壳体而成,壳体内径为23.5cm,高20cm;导线分为2盘,按同一方向缠绕在壳体外表面,每盘铜线非均匀地缠绕1200圈,2盘铜线起始端连接在同一接线柱上,末端连接在另一接线柱上,2盘铜线间距为13cm;底座由大理石打磨而成,内有一个160mm×160mm的凹槽.数字电桥测试仪可以产生额定频率的电流和额定电压,为线圈提供恒定的电压,并且可以同时测得线圈的电感值.

图1 电感试验装置Fig.1 Inductive test equipment
2 试验概述
2.1 试件制备
水泥(C):P·O52.5;粗骨料(G):石灰石碎石,最大粒径为20mm;细骨料(Sand):级配连续的中粗河砂;掺合料(A):粉煤灰;减水剂(S):聚羧酸减水剂,固含量(质量分数)25%,减水率(质量分数)25%~30%;钢纤维(SF):Maccaferri Wirand FF3HS端钩型钢纤维,长度50mm,直径0.75mm,抗拉强度1500MPa,约5770根/kg.混凝土强度等级为C50,基体配合比见表1;SFRC的水灰比m(W)/m(C+A)为0.311.

表1 基体配合比
试验制备了不同钢纤维含量(25、30、35、40、45、50、55kg/m3)的7组SFRC小梁试件,尺寸均为150mm×150mm×550mm;每组均有12个试件,共84个试件,记为SFA-B,其中A为纤维含量,B为试件编号,例如SF25-1代表纤维含量为25kg/m3、编号为1的SFRC试件.另外还制备了9个尺寸为150mm×150mm×300mm的普通混凝土棱柱体试件.在制备SFRC试件过程中,先将砂、粗骨料、粉煤灰和水泥依次加入搅拌机共同搅拌2min;待其充分混合后,再将水和减水剂均匀加入搅拌机中匀速搅拌3min,同时将钢纤维均匀地撒在搅拌机中.所有试件均在浇筑36h后拆模,并在温度(20±2)℃,相对湿度95%的标准养护室中养护至28d.
2.2 试验方案
2.2.1混凝土力学试验
按照GB/T 50081—2002《普通混凝土力学性能试验方法标准》,对养护28d的普通混凝土棱柱体
试件进行轴心抗压强度测试,得到普通混凝土轴心抗压强度平均值为77.54MPa.
根据EN 14651:2005《Test method for metallic fibre concrete—Measuring the flexural tensile strength(limit of proportionality(LOP), residual)》,采用最大试验力为200kN的万测ETM105D电子万能试验机进行SFRC切口梁三点抗弯试验.试件尺寸和试验布置见图2.试验前,在试件切缝的中线处对称粘贴2片薄钢片,将电子引伸计夹在这2片薄钢片中间;采用引伸计控制加载方式,在裂缝开口位移(CMOD)达到0.1mm之前,加载速度为0.05mm/min,此后加载速度为0.20mm/min,直到CMOD值达到4.0mm后停止试验,得到试件荷载-裂缝开口位移(F-CMOD)曲线.根据式(8)计算比例极限强度fLOP,以及CMOD值不同时的残余抗弯拉强度fR,j(j=1、2、3、4,分别表示CMOD值为0.5、1.5、2.5、3.5mm).根据EN 14651规定,贴了引伸计固定钢片的试件,需按式(9)计算其CMOD值.
(8)
(9)
式中:b、h分别为试件截面的宽度和高度,均为150mm;hsp为试件割缝顶到顶面的高度,(125±1)mm;L为试验时试件的跨距,500mm;F为试验时的荷载值,kN;CMODy为传感器测得的开口位移,mm.

图2 切口梁三点抗弯试件设计Fig.2 Design of three-point bending test specimen(size:mm)
2.2.2电感试验
在电感试验前,先将经过切口梁三点抗弯试验后的试件按图3(a)切割打磨成2个边长为150mm的立方体试块.为避免钢纤维“墙效应”对试验结果的影响,去掉试件两侧宽75mm部分.为了防止混淆测试结果,统一命名Z轴为垂直于试件浇筑面的轴,X轴为平行于试件短边的轴,Y轴为平行于试件长边的轴.本试验在每组纤维含量试件中随机选出5个试件进行切割,即每组纤维含量试件测试10个试块,7组共70个试块.
试验所用电感设备如图3(b)所示.测试前,先将数字电桥仪预热20min以保证测量值的准确性.

图3 电感试验方案Fig.3 Inductive test scheme
测试步骤为:(1)将试验设备和试块放在一个非铁磁性材料的台面上,保证其周围50cm范围内没有其他金属材料;设置电桥仪产生频率为1kHz的电流和1V的电压,激发磁场并测得空线圈的电感值.(2)将试块浇筑面朝上(Z轴)放入线圈中央,测出线圈电感值,计算得到电感增量ΔLZ;以此类推,依次测得X、Y轴的电感增量ΔLX、ΔLY.为保证测试数据的准确性,每个试块在每个方向上都围绕线圈的缠绕方向转动3次测量,取其平均值作为测试结果.电感试验完成后,从每组纤维含量的10个试块中随机选取1块,用压力机将其完全压碎,并用磁铁将其中钢纤维全部取出,清洗后烘干称重.
3 试验结果和讨论
3.1 切口梁三点抗弯试验结果与分析

图4 钢纤维混凝土三点抗弯试验F-CMOD曲线Fig.4 F-CMOD curves of three-point bending test with SFRC
图4为切口梁三点抗弯试验得到的荷载-裂缝开口位移(F-CMOD)曲线.由图4可知,在试件开裂之前,曲线均呈现从线性到非线性变化的过程,这与普通混凝土试件切口梁三点抗弯试验结果类似.在试件开裂以后,F-CMOD曲线可分为屈服型和强化型2种,其中的屈服型曲线表现为试件开裂后承载力陡然下降,其值小于开裂荷载,主要有SF25、SF30、SF35这3组试件;强化型曲线表现为试件开裂后,其承载力不降反升,曲线呈现应变硬化趋势,主要有SF40、SF45、SF50、SF55这4组试件.
曲线OA段为线弹性变形阶段,此时钢纤维在锚固黏结力作用下与混凝土基质协同变形,抵抗荷载;当荷载继续增大时,SFRC进入弹塑性阶段(AB段),此时混凝土内微裂缝不断发展,但由于应变较小,钢纤维发挥作用不大.这2个阶段与普通混凝土试验过程基本一致.
对于屈服型曲线,当荷载达到混凝土开裂荷载时,混凝土开裂,曲线进入BC段,此时由于试件中的钢纤维含量较少,不能有效阻止裂缝的发展,因试件截面刚度下降导致其承载力下降,但是较大的变形使高弹性模量的钢纤维产生了较大应力,通过桥接裂缝两端,阻止了混凝土的进一步破坏;继续施加荷载后,试件进一步变形,钢纤维应力快速增加,当变形超过某一值后,钢纤维的应力值达到较高水平,其影响超过混凝土开裂的影响,导致试件截面刚度有所回升,因此其承载力随变形而增大,曲线逐渐上升(CD1段),发生了应变硬化现象;钢纤维桥接于混凝土裂缝两端,其应力最终通过黏结锚固作用传递到混凝土基质中,若该应力过大,将导致其端部黏结锚固力超过黏结锚固强度,钢纤维被逐渐拔出,试件承载力下降,同时裂缝继续发展,曲线进入D1E1段.
强化型曲线无明显屈服段.由于试件中的钢纤维含量较高,可能导致B点对应荷载有略微提高;同时由于钢纤维含量高,在混凝土裂缝刚产生时,钢纤维就能有效控制裂缝发展,试件截面刚度不会下降,甚至由于钢纤维较大的应力而导致试件承载力缓慢上升,曲线直接进入BD2强化段;当纤维黏结锚固作用被破坏后,与屈服型曲线一样,曲线进入D2E2段.另外还可看出,无论是屈服型曲线还是强化型曲线,当CMOD达到3.5mm时,钢纤维混凝土试件仍旧表现出较好的韧性.
当普通混凝土梁加载时,一旦裂缝出现便迅速延伸至顶部,导致试件断裂失效,表现出明显的脆性.而SFRC破裂后,钢纤维与基体间的界面黏结力可以传递荷载,使得SFRC具有一定的韧性和延展性.图5为各项强度指标试验结果对比图.由图5可见:SF25组试件的极限荷载(fR,max)为6.97MPa,若以此为基准,则SF30、SF35、SF40、SF45、SF50、SF55组试件的极限荷载提高了4.45%、10.04%、10.62%、14.06%、33.29%、38.31%,说明纤维含量的增加可以大幅提升SFRC的抗弯承载力;纤维含量对比例极限强度(fLOP)的影响不大,这是因为在开裂之前,混凝土和钢纤维共同承担荷载,钢纤维尚未起到阻裂作用;对于fR,1,fR,2,fR,3,fR,4而言,纤维含量对其影响较大,尤其是当纤维含量为35、50kg/m3时,试件的残余抗弯拉强度增加明显,而其余纤维含量试件的残余抗弯拉强度变化不大,这为SFRC结构设计时选取钢纤维含量提供了参考.

图5 不同含量钢纤维混凝土强度指标比较Fig.5 Comparison of strength index of SFRC with different steel fiber contents
3.2 电感试验结果与讨论
电感试验后,得到每个立方体试块在3个方向上的电感增量ΔLX、ΔLY和ΔLZ.随后,在每组纤维含量试块中随机取出1块,将其破碎后,使用强力磁铁提取其中的钢纤维称重.对每组试块的纤维含量及其电感增量进行线性回归分析,如图6所示,当相关系数超过0.99时,表明纤维含量与电感增量具有明显的线性关系,通过电感试验可以很好地确定纤维含量.计算得到ω值为11.932,对于相同类型的钢纤维,ω是1个常数,它不受试件内纤维分布的影响.
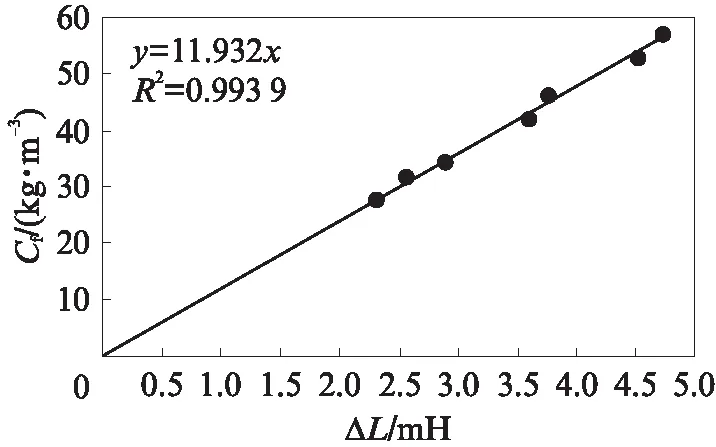
图6 电感试验中纤维含量与电感增量的关系Fig.6 Relationship between ΔL and Cf based on inductive test
表2展示了每组SFRC试块的电感增量、纤维含量以及X、Y、Z方向上纤维方向数ηX,ηY,ηZ的试验结果及其变异系数(CV).通过对比可以看出,电感试验得到的纤维含量均值(Cf)与设计含量的差别最大仅6.4%,这说明电感试验方法可以很好地检测纤维含量;X、Y方向上的纤维方向数变异系数随着纤维含量的增加而变小,这说明纤维含量的增加使得SFRC梁内的纤维分布更加均匀,对于SFRC梁力学性能的提升也更加明显.纤维是随机分布于混凝土基质中的,若纤维含量较少则某区域含有钢纤维的几率将下降.因此,钢纤维只有达到一定含量后才会分布均匀,且均匀性随着钢纤维含量的增加而增大.

表2 钢纤维混凝土电感试验结果
表3为各组SFRC试块的纤维方向数相对比例CX,CY,CZ.由表3可见,在SFRC试块中,纤维方向数在X、Y、Z方向上的相对比例大致为1.2∶1.4∶1.0,与纤维含量的关系不大.这是因为纤维在试件中的分布主要受模具、纤维形状和振捣方式的控制.试件制作时通过振动台振捣,在振捣过程中纤维会朝特定方向发生旋转和排列.具体而言,外部振动时,纤维在重力作用下会向水平方向旋转,试件受振动越多,纤维越倾向于分布在水平面上,因此Z方向上分布的纤维最少.此外,纤维在Y方向上分布的比例均大于X方向,这主要是模具“墙效应”的影响(见图7),在模具壁附近,本可以沿X方向分布的钢纤维在模具壁的阻挡下会朝Y方向倾斜,也因此“墙效应”的影响范围一般为纤维长度的一半.
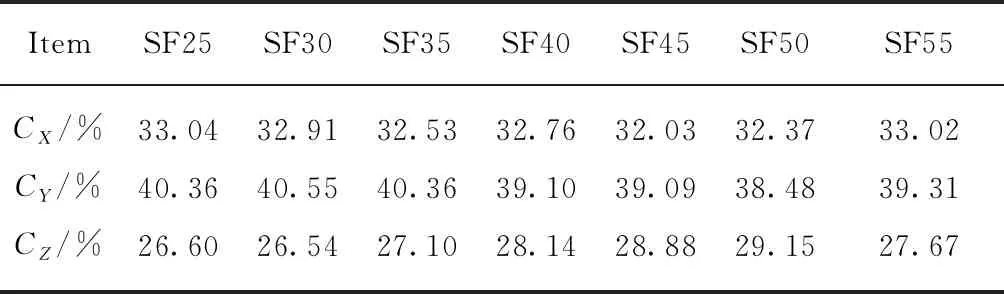
表3 各组SFRC试块的纤维方向数相对比例

图7 钢纤维混凝土模具“墙效应”示意图Fig.7 Wall effect in SFRC mould
4 结论
(1)纤维含量不同时,SFRC试件的荷载-开口位移曲线形状不同.当荷载达到比例极限后,纤维含量低于40kg/m3的试件有明显的屈服下降段,而纤维含量大于40kg/m3的试件无明显的屈服下降段,直接进入了应变硬化阶段.
(2)根据切口梁三点抗弯试验结果得到了不同纤维含量SFRC试件的残余抗弯拉强度,发现纤维含量为35、50kg/m3时,纤维的增强效果会明显增加,而其余纤维含量试件的残余抗弯拉强度变化不大.
(3)通过电感试验测得SFRC试件的实际纤维含量与设计含量最大仅相差6.4%,表明电感试验可以很好地评估SFRC试件中的纤维含量.
(4)纤维方向数在X、Y、Z方向上的相对比例大致为1.2∶1.4∶1.0,与纤维含量关系不大;由于模具“墙效应”的影响,纤维在Y方向上的分布比例均大于X方向;此外,随着纤维含量的增加,纤维在SFRC试件中分布更加均匀.
