考虑多车型的公交组合服务方案优化

李 雪，朱一洲

（华南理工大学 土木与交通学院，广州510641）

现阶段，我国大多数城市实行单一车型的全程车公交运营服务方案，但随着客流需求呈现时空上的异质性，极易出现高峰拥挤、平峰空驶等现象。 为了平衡需求与运力的矛盾， 组合服务方案应运而生， 即加开区间车或大站快车来辅助全程车运行，以实现客流的快速集散。

国内外已有研究表明组合服务方案能够提高公交运营效益和乘客出行效率。如文献[1-5]研究证明了组合服务方案降低了运营成本和乘客的车内时间，然而这些研究较少考虑多种车型。 文献[6]对全程车发车频率和车型进行了优化；文献[7]研究了单一车型和多车型的调度优化模型，但未考虑容量限制；文献[8]研究表明，大小车型的全程车运营方案较单车型的全程车更经济，但未考虑与其他模式的组合优化问题。 为此，基于线路客流的异质性，考虑将车型与全程车、区间车和大站快车的服务模式相结合，以乘客出行成本和公交运营成本最小为目标，以发车频率、容量限制、车队规模为约束，构建车型选择与组合服务方案的同步优化模型，并结合枚举与遗传算法求解，对乘客出行与公交运营进行协调优化研究。

1 问题描述

考虑多车型的公交组合服务方案的研究问题可描述为：某线路的公交按照全程车、区间车和大站快车的组合服务方案运行，不同车型的车辆对应不同服务模式，停靠不同站点，到达终点后等待下一次发车。

2 模型与算法

2.1 模型假设

在此基于单条公交线路的研究，提出以下模型假设：①乘客到站服从均匀分布；②全程车与区间车为站站停服务；③仅考虑站站停公交与大站快车的一次换乘，不计换乘费用；④多车型指大、中、小等3 种车型（即J=3），且认为道路满足开行要求；⑤研究路线的日客流量变化幅度较小，忽略特殊情况造成的乘客需求变化。

2.2 模型建立

2.2.1 需求分析

考虑乘客的换乘需求，以乘客出行服务模式选择为基础，将该需求进行分类。 具体如下：

r=1 大站快车直达；

r=2 乘客在中间站点y 处由大站快车换乘慢行公交；

r=3 慢行公交直达；

r=4 乘客在中间站点z 处由慢行公交换乘大站快车。

在此，以乘客出行时间为效用函数，利用Logit模型，确定大站快车服务客流需求的百分比Ψij为

式中：tWijr，tRijr，tIijr分别为从站点i 到站点j 的第r 类需求的平均候车时间、平均换乘时间、平均车内时间；θW，θR，θI为客流需求对候车、换乘、车内时间的敏感性参数；λi为决策变量， 表示大站快车是否停靠站点i：取λi=1，停靠；λi=0，越站。

在中间站点z 处， 换乘大站快车到达终点j 的客流需求百分比为

2.2.2 乘客出行成本

乘客出行成本CU包括乘客候车时间成本CW，换乘成本CR和车内时间成本CI。 由于不同车型的车容量不同，其发车频率也会随之变化。 因此，站站停公交和大站快车使用车型J 时， 其发车频率分别为fijJ和fEJ。

1）候车时间成本CW

式中：μ 为用户时间价值；αW为候车时间因子，由假设条件1，取αW=0.5。

2）换乘时间成本CR

换乘仅发生在大站快车与站站停公交服务之间，换乘时间为

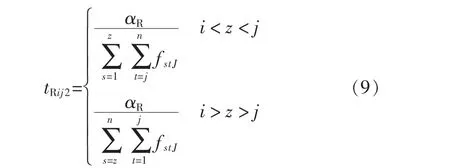
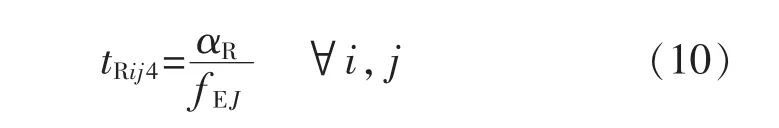
式中：z 为换乘站点；αR为换乘时间因子， 由假设条件1，取αR=0.5。

3）车内时间成本CI

式中：tIijr为车内时间， 等于车辆行驶时间与站点延误时间之和。 有：

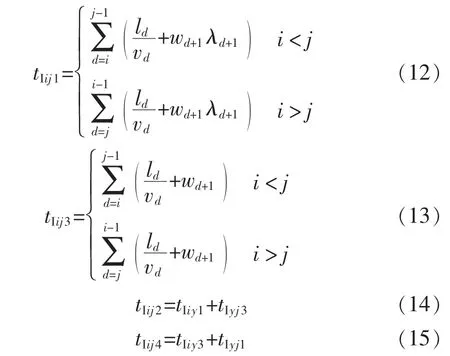
式中：ld为站点d 与站点d+1 的间距；vd为从站点d到站点d+1 的车辆平均运行速度；wd+1为站点d+1的平均延误时间。

2.2.3 运营成本

运营成本CO包括基础设施、人员费用相关的运营时间成本Ct和车辆燃料消耗等相关的运营里程成本CL[9]。 不同车型的运营成本不同。 即：

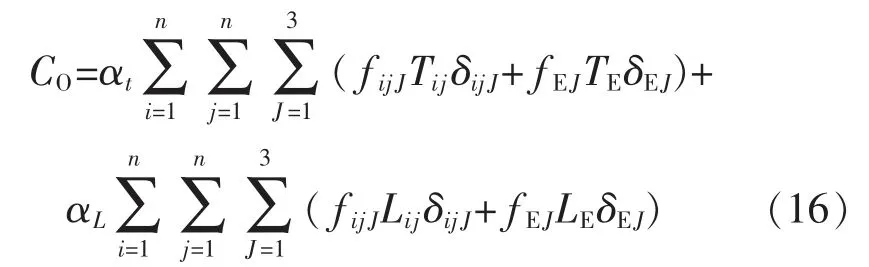
式中：αt为单位时间运行成本；αL为单位里程运行成本；Tij，TE分别为站站停公交、大站快车的运行时间；Lij，LE为对应的运行里程；δijJ，δEJ分别为车型选择的决策变量，取值1 或0。

系统总成本Ctot定义为CU和CO的加权和，即：

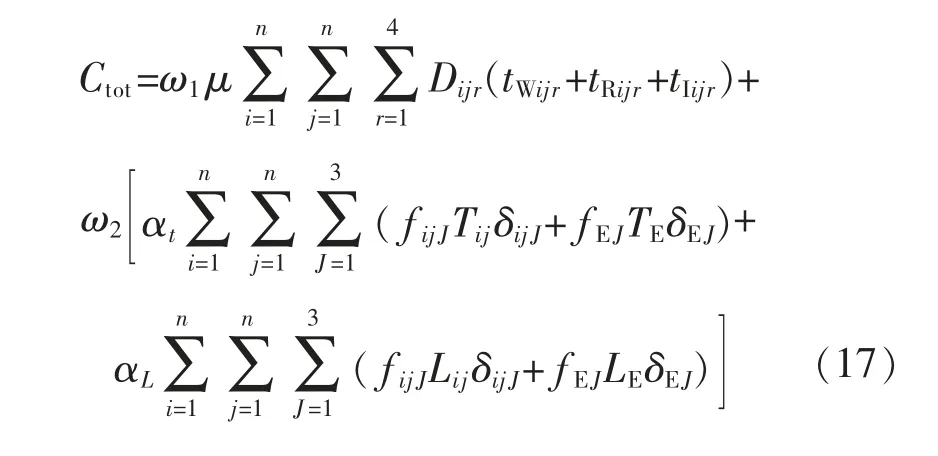
其中

式中：ω1，ω2分别为用户成本、运营成本的权重值。

2.2.4 约束条件

1）上下行发车频率守恒。 即：

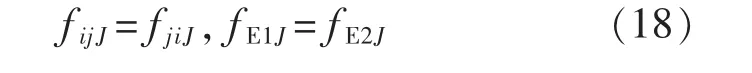
2）容量限制。 路段l 的平均发车间隔hijl，hEl必须分别小于等于其最大发车间隔Hijl，HEl。

最小发车间隔与发车频率有关，最大发车间隔与车容量和路段l 的最大乘客需求有关。 则：

式中：Oijl，Iijl分别为上、下行乘客的最大断面客流；b为车辆满载率。 同理可推得大站快车（HEl）的情况。

3）车队规模保证发车频率满足需求。 即：

2.3 求解算法

所建模型的决策变量为各服务模式及其发车频率、大站快车越站情况和车型选择，为非线性混合整数规划问题。 由于大规模公交问题计算复杂，现阶段均采用启发式方法求解。 故在此结合枚举法和遗传算法来求解模型。 其过程如下：

步骤0随机枚举生成不同服务模式的车型组合及频率；

步骤1判断是否满足需求及车队规模，满足执行步骤2，否则回到步骤0；

步骤2得到发车频率集合，选择其中一组可行解；

步骤3判断是否为最后一组解，是则输出优化方案，否则执行步骤4；

步骤4遗传初始参数设置，确定种群规模M和迭代次数N；

步骤5根据可行解生成初始种群，并转换为二进制编码；

步骤6将目标函数作为适应度函数进行计算；

步骤7判断是否满足迭代条件t＞N， 满足则输出最优结果，并回到步骤2，否则执行步骤8；

步骤8进行遗传操作——选择、交叉、变异，产生第t 代种群；

步骤9计算子代t 的个体适应度值，并储存最优解，t=t+1，返回步骤7。

3 实例分析

广州市某公交线路全长为22.9 km，平均行驶速度为20 km/h，载客容量为80 人/辆，发车间隔为8～10 min，目前该线路以全程车的服务方案运行。设定研究时段为1 h，早高峰7：00—8：00 的公交客流及站距信息见表1，其他参数见表2。

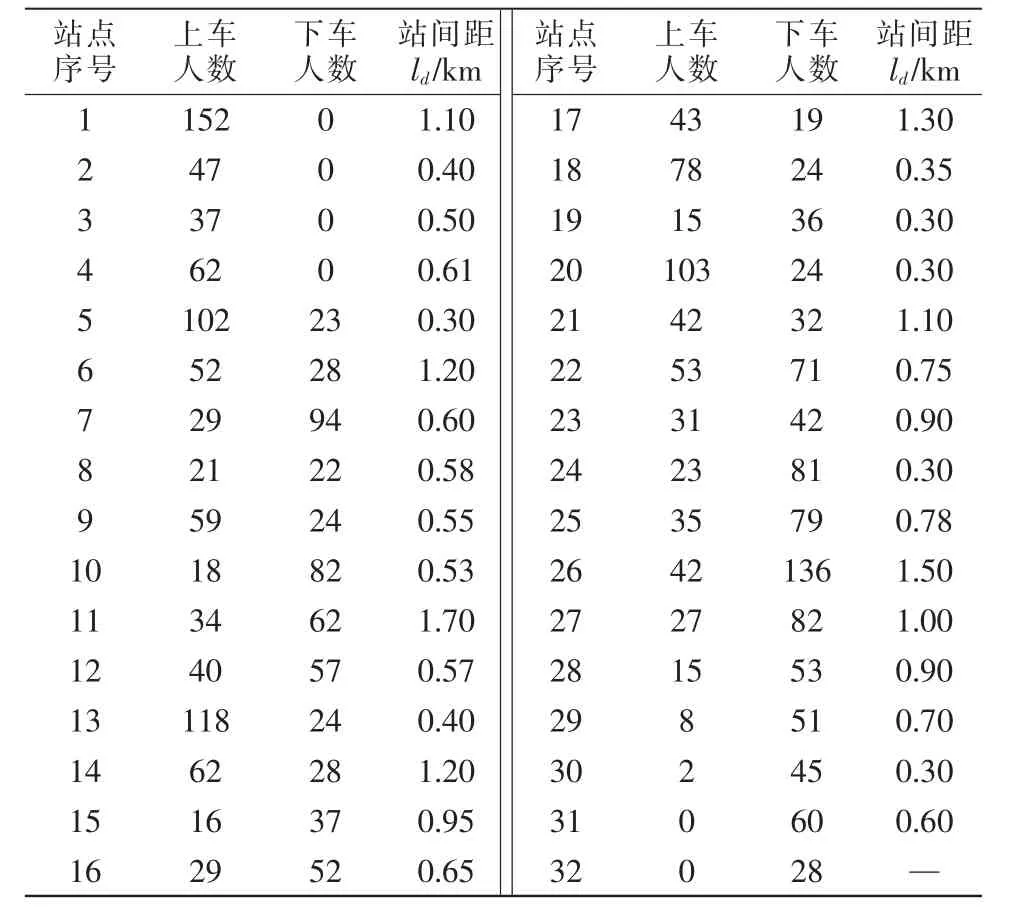
表1 公交客流及相关参数Tab.1 Bus passenger flow and relevant parameters

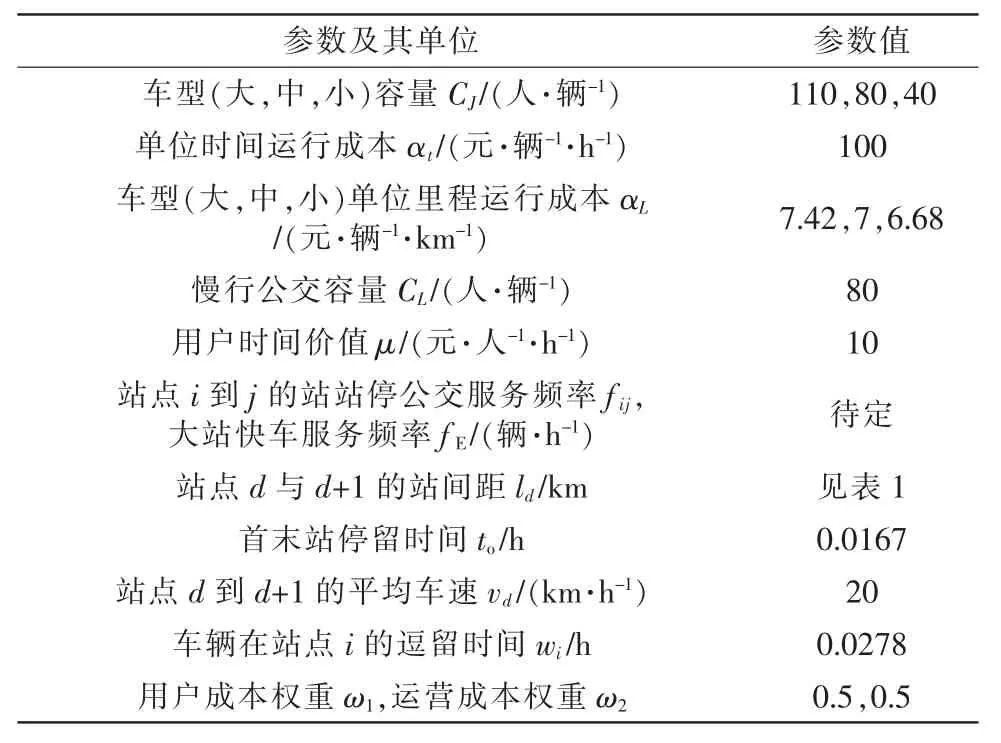
表2 模型参数的取值Tab.2 Values of model parameters

根据表1 提供的数据，计算断面不均衡系数确定区间车潜在折返点为站点7，14，18，22，25。 再由文献[10]的客流反推方法得到公交客流的出行OD（origin-destination）。

3.1 结果分析

优化结果见表3。

表3 模型最优解Tab.3 Optimal solution of model

由表3 可知，研究时段内共计发车7 辆，区间车运行区间为站点1—站点22 和站点22—站点25，大、中、小车型分别发车2，5，0 辆；乘客出行成本为10057.56 元， 公交运营成本为5173.31 元，加权总成本为7615.44 元。

在研究时段内， 站站停公交实际为中型车，其与不同车型的快车组合服务。 多车型组合服务方案的对比见表4。结果表明，多车型组合的服务方案比单一车型的组合服务方案经济效益更好。

表4 多车型组合服务方案对比Tab.4 Comparison of multi-vehicle-size integrated service plan

在研究时段内，4 种运营服务方案最优结果的对比见表5。由表可知，方案Ⅰ全程车最优发车频率为7 辆/h，加权总成本Ctot为8098.31 元；与方案Ⅰ相比， 方案Ⅱ全程车+区间车的总成本Ctot降低了3.43%，公交运营成本CO降低了18.62%，但由于线路部分站点发车频率下降，导致候车成本增加。 加入大站快车的方案Ⅲ与方案Ⅰ相比， 其Ctot下降了2.47%，由于考虑换乘需求及车辆越站，换乘费用CR增加81.65 元/h，候车成本CW也增加了668.48 元/h。方案Ⅳ全程车+区间车+大站快车与其他3 种方案相比，Ctot分别降低了6%、2.61%和3.58%。

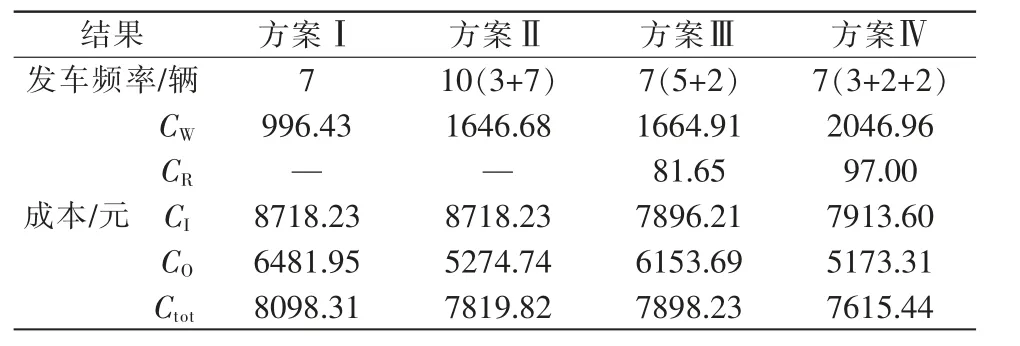
表5 不同服务方案的对比Tab.5 Comparison of different service plans

3.2 参数分析

客流直接影响公交的运营服务方案，为此研究了OD 变化对相关结果的影响。OD 倍数的影响如图1 所示。

4 结语

通过研究考虑多车型及不同模式的公交组合服务方案优化问题，提出了多车型的公交组合服务方案优化方法。 案例分析结果表明，所开发的模型可用于公交运营方案制定和调度优化，且具有实用性；对比不同方案的最佳结果，证明了方案Ⅳ——多车型的全程车+区间车+大站快车的组合服务方案，比单一模式服务和单一车型的组合服务方案经济效益更好。 从公交系统整体来看，其产生的效益足以弥补增加的候车时间和换乘时间成本的增加；通过调整OD 需求，采用该优化方法还可以帮助决策者协调乘客与运营商的利益，找到折中运营方案。

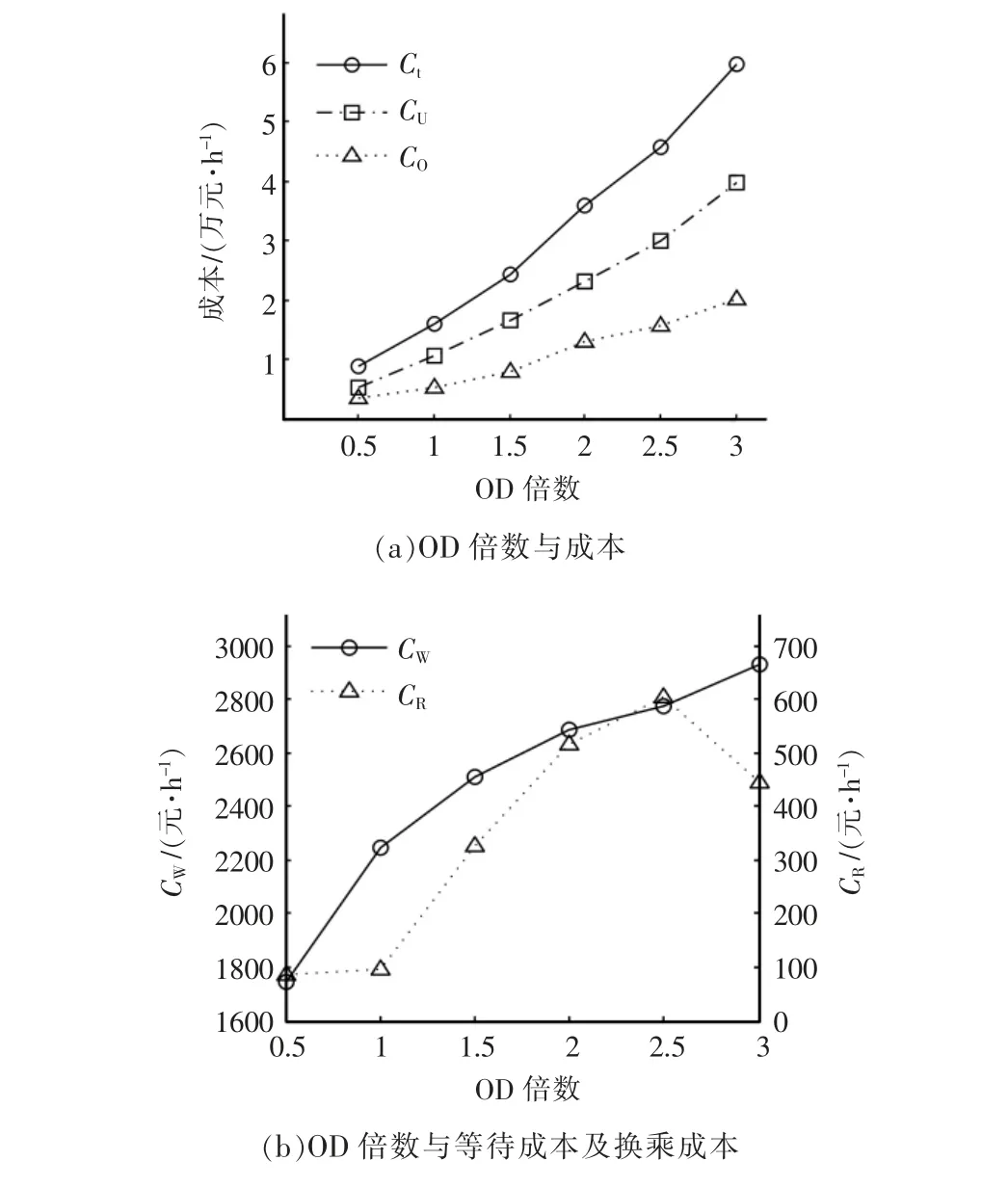
图1 OD 倍数对相关结果的影响Fig.1 Effect of OD multiple on correlation results