基于欧式距离角点提取的工业机器人视觉算法
2020-08-28赵潇安
赵潇安
(桂林电子科技大学 电子工程与自动化学院,桂林541004)
工业机器人在物体抓取、自动装配、喷涂、搬运码垛、焊接等场合的应用越来越广泛[1]。 与使用传统的示教方法搭建机器人抓取系统相比较,基于视觉的工业机器人抓取系统, 提升了其灵活性和稳定性,极大地拓宽了工业机器人的应用空间。
在2D 相机的工业机器人视觉研究中, 文献[2]使用发那科FANUC 机器人通信模块与标定算法,通过图像处理提取轮廓中心为特征点;文献[3]提出基于图像梯度优化与评分的方法,以解决目标物体的识别与定位问题;文献[4]采用最小二乘算法拟合直线, 然后根据直线计算目标物体的倾斜角度;文献[5]提出基于直线特征的位姿测量方法SoftNewton,构建了直线的匹配评价函数, 再采用高斯牛顿迭代算法解算目标位姿;文献[6]采集2 幅图像通过双视图几何的等效约束来解算目标物体的旋转姿态角度。
为了有效地提取目标物体的姿态角度信息,在此提出根据聚类中心之间中点与角点之间的欧式距离提取角点的方法,然后以角点作为特征点提取虚拟向量,采用相互匹配的向量计算出目标物体的姿态角度。
1 工业机器人图像数据采集平台搭建与图像预处理
1.1 工业机器人图像数据采集平台
为了通过图像获取工业机器人的末端姿态数据,搭建工业机器人图像数据测量平台。 平台硬件由垂直多关节六自由度重复定位精度为0.03 mm 的机器人,图像分辨率为2048×1536 和水平/垂直像素为3.45 μm×3.45 μm 的摄像机, 以及工业计算机等组成。
在工业机器人视觉系统中,上位机通过以太网总线的通信方式与工业机器人控制系统通信。图像处理软件采用德国MVtec 公司研发的HALCON机器视觉软件, 利用导出的C# 文件开发工业机器人通信模块。 工业机器人图像数据测量平台如图1所示。
1.2 工业机器人视觉系统标定与摄像机图像畸变矫正
图像数据测量平台摄像机安装方式采用eyeto-hand 结构,将工业摄像机固定在支架末端。 通过手眼标定计算得到工业摄像机坐标系在工业机器人基坐标系中的位置。 使用文献[7]的标定算法得到摄像机内外参数,通过计算获得图像的内部参数与标定板所处平面坐标系相对于相机坐标系的转换关系。
畸变图像以及通过图像畸变矫正后得到图像的复原图,如图2 所示。
2 目标物体几何元素计算
目前, 基于2D 视觉的工业机器人抓取系统多采用SIFT,SURF[8-9]等特征检测算法。 然而,这些算法的特征点检测依赖于尺度空间的选择,在实际使用过程中不可避免地存在特征点的漏检。
2.1 粗角点计算
在图像的微观结构中,图像的边缘轮廓由微小的像素构成。 以三角柱和立方体的平面拍摄图为例,目标物体的角点作为特征点。在此通过模板a 与模板b 遍历图像中所有的边缘像素点,若该像素点拥有2 个灰度变换方向,则保留该点为粗角点。
2.2 基于两个聚类中心之间的中心点角点估计
在几何目标物体的平面图中,轮廓可以被描述为由多个三角形组成。 在如图3 所示立方体的轮廓内可以提取出三角形r1,r2;在如图4 所示六棱柱的平面图中可以提取出三角形R1,R2,R3。 由此分析可知,角点的分析涉及构成几何的基本单元——三角形。 故在此对典型的基本单元三角形进行角点提取的研究。

图3 立方体平面图轮廓三角形划分Fig.3 Cube plan view outline triangle division
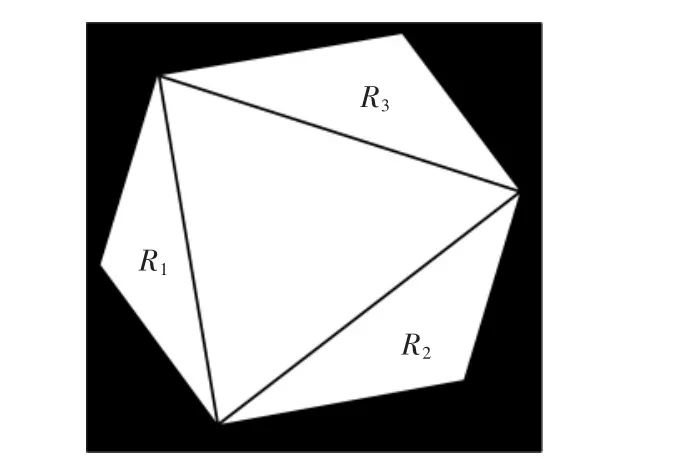
图4 六棱柱平面图轮廓三角形划分Fig.4 Hexagonal prism plan view outline triangle division
边缘锯齿以及角点、伪角点与轮廓内一点之间的欧氏距离如图5 所示。 图中,图像中存在边缘锯齿等干扰因素,造成在角点检测中存在大量的伪角点。 在闭合轮廓中,真角点与轮廓内其它点的欧式距离存在唯一性,并且存在欧式距离最大值。
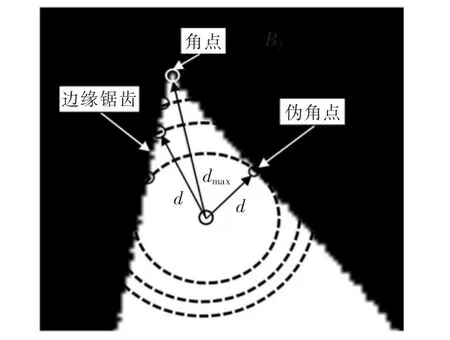
图5 边缘锯齿以及角点、伪角点与轮廓内一点之间的欧氏距离Fig.5 Edge jagged and Euclidean distance between corner,false corners and a point in the contour
由图可见,轮廓内的点与角点之间的欧式距离为dmax,与伪角点之间的欧式距离为d,dmax>d。 故在此提出计算欧式距离最大值的方法,通过欧式距离剔除由于伪角点引入的不稳定因素。
2.3 角点提取
为了得到更加准确的角点,在图像处理过程中引入k-means++修正算法[10]。通过上述方法计算出粗角点之后,选择合适的聚类中心数,计算获得所需的聚类中心。
2.3.1 基于两个聚类中心之间的中心点角点提取
计算出聚类样本与聚类中心之后,可计算出其中2 个聚类中心之间的中心点坐标。 如图6 中聚类中心点ci与中心点c¯所示,有

如图6 所示,计算中心点分别与其它聚类样本内的粗角点(真角点与伪角点)之间的欧式距离d 为


图6 聚类中心的中心点与粗角点之间的欧式距离Fig.6 Euclidean distance between the central point of the cluster center and the rough corners
在其它聚类样本内,分别保留拥有最大值d 的对应粗角点为真实角点。在图6 所示B1区域内,dmax>d1,dmax>d2,保留拥有最大值dmax的粗角点即A2为真角点。 使用其它的聚类中心组合与聚类样本可重复以上计算过程,计算出各个角对应的角点。
2.3.2 验证
为提高角点识别的正确率,对所提取的角点进行验证。
步骤1在提取出的真实角点之间计算中心点,类似于式(1),重新计算中心点。
步骤2在各个聚类样本中, 重新计算新得到的中心点与粗角点(真角点与伪角点)之间的欧式距离,保留欧式距离最大的对应角点为真实的角点。
步骤3在每一个聚类样本中, 选取与验证前不同的中心点, 估计同一角点。 分2 种情况进行讨论:
情况1计算出2 个角点。 若验证前与验证后得到的角点相同,则该点为最终计算真角点;
情况2若验证前与验证后得到的角点不相同,则重新计算2 个角点与对应的聚类中心之间的距离,距离最小者为最终计算的真角点。重复步骤1至步骤3,直至所有的角点验证完毕,得到目标物体的所有的真角点。
3 虚拟向量提取与姿态旋转角度计算
3.1 虚拟向量提取
在立方体平面图中,采用与对角线平行的虚拟向量L1与L2为特征向量。 三角柱平面图中采用与三角柱的边平行的L1′和L2′为虚拟向量, 并以此作为特征向量。 三角柱平面图与立方体平面图的虚拟向量如图7 所示。
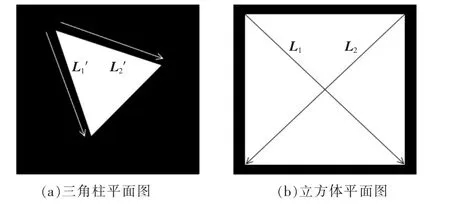
图7 平面图的虚拟向量Fig.7 Virtual vectors of floor plan
3.2 根据虚拟向量计算姿态旋转角度
目前,目标物体的姿态旋转角度计算方法主要采用SIFT 算法和SURF 算法等提取图像中的特征点,通过估算仿射参数计算姿态旋转角度。 文献[11]提出采用BRIEF 描述子对SURF 算法提取的特征点进行描述,结合最近汉明距离融合PROSAC 算法提高特征点的匹配精度。
文献[12]将软决策技术和POSIT 算法[13]结合,形成SoftPOSIT 算法。 文献[14]采用尺度不变特征变换SIFT 算法计算特征点,采用特征点主方向匹配特征点并且计算姿态旋转角度,算法计算误差约为3°。
本文算法也采用假设与检验的方法,通过相互匹配的特征向量之间的夹角计算姿态旋转角度。 立方体起始姿态如图8 所示,先使用相机拍照一个固定放置目标物体的图像,将其作为模板图像,且目标物体的起始姿态为0°。 姿态的计算目的,就是获得从模板图像到实际目标的变化包括姿态旋转角度,从而为工业机器人末端抓取提供移动信息。

图8 立方体起始姿态Fig.8 Origin posture of the cube
在图像坐标系中, 立方体姿态旋转角度θ 为30°,如图9 所示。 立方体相对于模板图像的起始位置出现了姿态旋转角度θ,即目标图像。 由于姿态旋转角度的唯一性,通过目标图像与模板图像中目标物体之间的比较,获得工业机器人末端抓取的姿态旋转角度。

图9 立方体姿态旋转角度30°Fig.9 Cube posture rotation angle of 30 degrees
通过本文算法计算出目标物体的姿态旋转角度。 针对立方体平面图的4 个角点与三角柱平面图的3 个角点,以2.3 节获得的角点为基础,目标图像的虚拟向量、模板图像的虚拟向量为
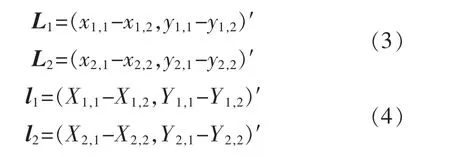
式中:(xi,j,yi,j)为模板图像的角点坐标,i=1,2,且j=1,2;(Xi,j,Yi,j) 为目标图像的角点坐标;i 为对应虚拟向量标号;j 为虚拟向量对应的角点坐标序号。
计算出目标物体的特征向量之后。 首先假设目标图像与模板图像之间的其中一对特征向量相互匹配。 特征向量之间的夹角为
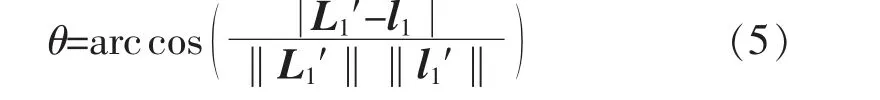
式中:假设L1与l1为互相匹配的特征向量;θ 为计算的旋转输出角度。 根据输出角度,计算仿射参数矩阵,并投影余下的特征向量。 即
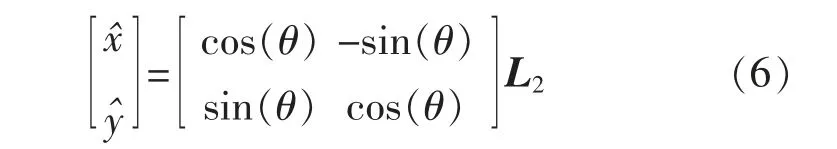
通过检验另外一条特征向量是否重合确定姿态,增加算法的稳定性。 若另外一条特征向量没有重合则重新匹配,计算出正确的姿态角度。
4 对角点识别和姿态角度估计算法验证
4.1 角点识别精确度分析
目标物体的边缘轮廓存在角点,如图10 所示。为了提取更加精确的角点,在此进行了方法的对比。 采用文献[15]所述方法根据角度阈值提取角点,试验中以粗角点两边夹角>8°为阈值。基于欧氏距离的角点识别方法,提取出聚类中心之中心点与其它样本内欧式距离最大的粗角点为真角点。

图10 立方体边缘轮廓角点Fig.10 Corners of cube edge contour
角点的识别精度见表1。由表可知,基于欧氏距离的角点识别方法识别精确度高,对所提方法的实现具有更好的使用效果。

表1 角点识别精度Tab.1 Corner recognition accuracy
4.2 目标物体姿态角度估计误差结果
通过试验验证本文算法,选取立方体与三角柱为试验图像。 目标物体的姿态旋转角度,如图11 所示。
在图像坐标系中,三角柱围绕旋转中心点从5°旋转至60°, 立方体围绕旋转中心点从5°旋转至85°。 在图像处理过程中,图像没有噪声等干扰的情况下,目标物体没有发生平移变换。
采用所提出的目标物体姿态角度估计算法,评估姿态角度的误差。 三角柱和立方体的姿态角度计算误差如图12 所示。
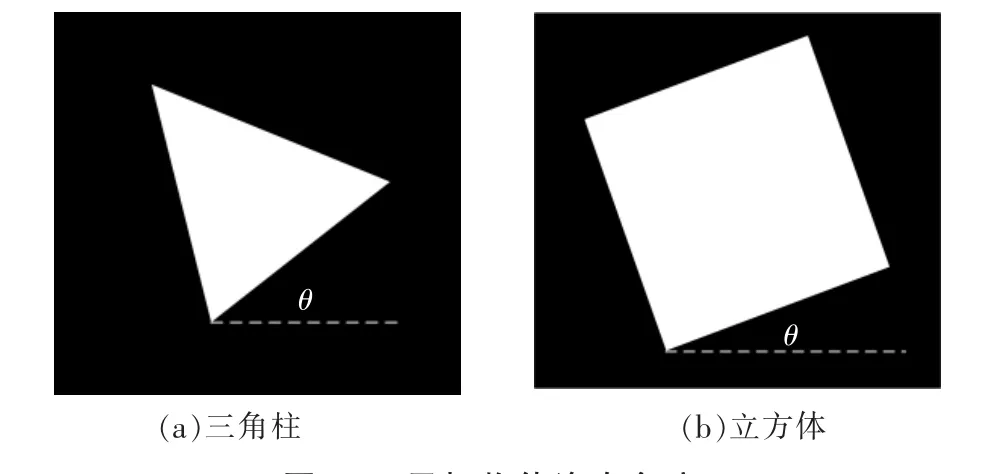
图11 目标物体姿态角度Fig.11 Posture angle of target object
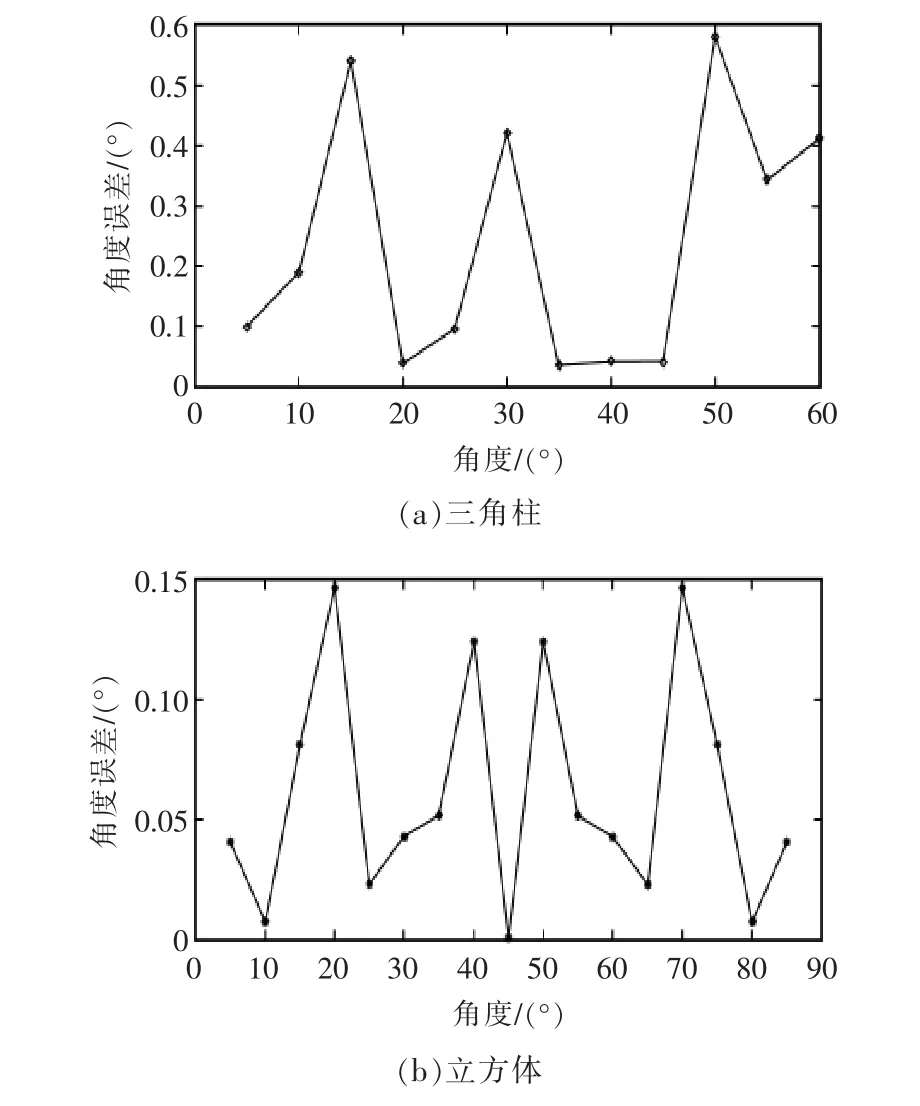
图12 目标物体姿态角度的计算误差Fig.12 Calculation error of posture angle of target object
由图可见,立方体的姿态从0°旋转至85°,最大误差达到0.1474°,平均误差为0.0610°;三角体的姿态从0°旋转至60°,最大误差达到0.5828°,平均误差为0.2367°。 SIFT 算法对于分辨率为640×480 的图像提取特征点需要1.75 s, 分辨率为320×240 的图像提取特征点所需时间为0.63 s; 本文算法运行时间小于0.2 s,缩短了图像中目标物体姿态旋转角度的测量时间。
4.3 姿态旋转角度估计算法试验对比分析
试验中,利用图11 所示立方体的平面图与三角柱的平面图为试验对象。 采用尺度不变特征变换SIFT 算法提取图像特征点,计算出模板图像与目标图像中对应匹配的3 个特征点后,采用三点法计算出仿射参数与姿态旋转角度。
三角体的姿态旋转角度分别为5°,10°,15°,20°,25°,30°,35°; 立方体的姿态旋转角度分别为5°,10°,15°,30°,35°,40°,45°,50°,55°,60°,75°,80°,85°。 本文算法与SIFT 算法的估计误差对比结果如图13 所示。

图13 目标物体姿态角度估计误差的对比Fig.13 Comparison of posture angle estimation errors of target objects
估计误差的试验对比结果见表2。 通过试验对比,本文提出的算法在物体旋转姿态角度估计上准确度优于SIFT 算法。
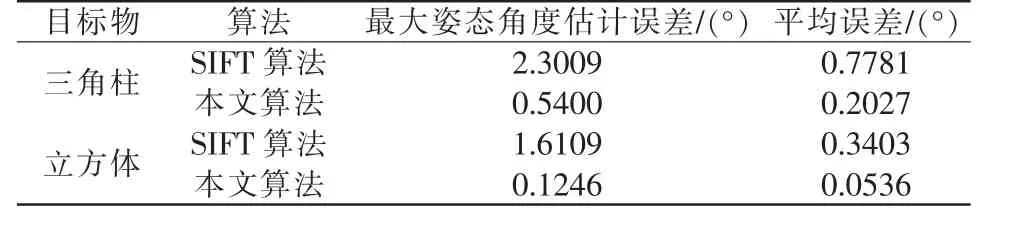
表2 姿态角度估计误差的对比结果Tab.2 Comparison results of posture angle estimation error
5 结语
在工业机器人末端目标物体的姿态获取中,角点的准确提取为一个关键技术。 所研究的图像可以抽取为多个三角形组成的独立单元。 在各个独立的三角形中,根据2 个聚类中心之间中点与角点之间的欧式距离为依据,提取拥有最大值的粗角点为真角点。 以角点构成图像的特征向量,采用假设与检验的方法将模板图像与目标图像中的特征向量相匹配,以相匹配的特征向量之间的夹角作为目标物体的姿态旋转输出角度,所获得工业机器人的末端姿态,为视觉抓取提供必要的参考数据。 基于试验采集图像数据进行了处理与分析,与尺度不变特征变换SIFT 算法作比较。 试验结果表明,所提出的方法用于目标物体的旋转角度估计具有较高的准确度,在实时性方面也表现出一定的优势。
