"求同”和“求异”思维在小学数学教学中的应用
2020-08-27谢红梅
谢红梅

【摘 要】在小学数学教学中,异中求同,同中求异,可以很好的引领学生理解数学知识,只有学生对数学知识的内在联系通了,才能转化为解题的能力,从而转化为数学素养。笔者在小学数学教学实践中,利用求同思维,打造知识体系,开启创新思维;利用求异思维,提升思维能力,改变思维模式,取得了很好的教学效果。
【关键词】小学数学教学;“求同”;“求异”;探讨
知识内容之间是存在一定联系,虽然小学阶段数学科目知识内容并不复杂,但是教师可以通过引导学生在学习基础知识时利用求同、求异思维理解、辨析并应用。本文旨在分析小学数学教学中的“求同”和“求异”思维应用,对具体教学手段进行了简要的分析,希望可以起到抛砖引玉的效果。
一、利用求同思维,打造知识体系
小学数学教学工作中,分数与百分数相关知识内容的实际应用能力培养是教学工作难点部分。不过笔者认为,学生在学习过程中,出色掌握了分数应用题的学生如果利用求同思维进行学习,往往在百分数应用题学习中也能有不错的学习效果;寻找百分数和分数应用题解题思路的相同之处,帮助学生形成将百分数视为分数的特殊形式的思维,并将两者进行转换,达到新旧知识,核心知识转换的目的。根据笔者观察,引导学生对比知识内容的类似部分后,学生很快就可以发现解题思路,例如二者解题前置条件为找准单位“1”,同样且必须理解数量关系(数据之间的比例关系)等。利用求同思维帮助学生利用已经学习过的知识辅助新知识的学习,达到巩固已学知识内容掌握程度,同时加强新知识内容的学习效果的目的。
我在实际的教学工作中,利用多媒体为学生展示了三道例题,1.八千克芝麻可榨取芝麻油两千克,请问工厂每千克芝麻可榨取芝麻油多少千克?芝麻出油率百分数为多少?榨取芝麻油1千克需要多少芝麻?2.九点六千克芝麻可榨取芝麻油二点四千克,请问工厂每千克芝麻可榨油多少千克?要榨芝麻油一千克需要准备的芝麻重量为多少?3.三十二千克芝麻可榨取芝麻油三十八千克,请问工厂每千克芝麻可榨取芝麻油多少千克?要榨取芝麻油一千克需要多少芝麻?根据笔者经验,学生学习小数和分数乘除法时,问题集中于“除数和被除数”部分,故笔者利用求同思维,通过第一个题目帮助学生察觉分数和百分数之间存在的共同点,引导学生理解:“分数”,“小数”看做整数,进而发现分数和百分数应用题解法无本质差别。
笔者认为单元知识内容之间存在一定的联系,教师在教学工作中须树立“求同存异”的思维模式,引导学生对各个知识点之间表层或本质内容进行梳理或推断,深化知识掌握程度并将其应用于具体的教学实践工作中,达到提高学生数学能力的目的。
二、利用求同思维,开启创新思维
小学阶段的数学教学工作中,教师需将学生思维能力培养作为工作重点,确保学生可以通过数学基础知识学习锻炼学生的创新思维能力,笔者认为在教学工作中利用求异思维可以有效开发学生的创新思维,而求异的前提条件为学生对知识内容间存在的联系有足够的了解。故教师在具体的教学工作中须有意识地让不同的知识点,在各个层面展现其互通之处,引导学生根据知识内容的互通之处来思考知识内容的差异,激活学生思维,引导学生对知识内容进行思考和推理,帮助学生高效掌握知识内容。
例如,在小学数学圆柱相关的教学工作中,笔者为引导学生对圆柱体体积公式进行推导,首先带领学生回顾知识内容,引导学生回忆正方形、长方形、圆的面积计算公式,及其推导过程,重点复习“圆”如何转换为““长方形”。引导学生正方体和长方体的体积计算公式及其推导过程,完成复习工作后,提出思考问题,“圆柱体的体积计算公式和长方体体积计算公式是否存在关联?”大部分学生可以发現圆柱体体积计算公式本质和长方体体积计算公式无本质区别,主要差异在于圆柱体底面积为圆,长方体为长方形。故圆柱体体积计算公式只需要将长方体体积计算公式中的长方形底面积换为圆的面积,故圆柱体体积计算公式为圆的底面积×高。
笔者通过课前知识内容复习引导学生回忆已学知识内容,并引导学生发现体积计算公式的本质为底面积×高;达到了在教学工作中渗透了“求同”数学思想的目的,帮助学生不受限于单元知识内容限制,从全局角度进行创新思考。
三、利用求异思维,提升思维能力
数学学习可以强化学生思维能力,学生通过推导公式和频繁的数据计算保持自身思维能力的敏锐性,而笔者认为“求异”思维可以有效提高学生思维能力训练效果。在小学阶段的数学教学工作,教师可引导学生对知识内容进行分析、推断,找出各知识点间存在联系和差别。
例如,在进行三角形相关的教学工作时,我首先通过多媒体展示了一道题目,一个底边长为四厘米,高为三厘米的三角形,其面积为多少平方厘米?我引导学生思考如何计算三角形面积。部分学生想要通过“画方格”(在草稿本上画出由边长为一厘米正方形组成的“大正方形”,一种帮助学生通过计算小正方形数量确定图形面积的方法)的方式计算三角形的面积,但实践后学生发现数方格无法准确计算三角形的面积,经过我的引导,学生讨论后发现可以将三角形转化为其他图形进行面积计算,我抓住时机引导学生通过拼接和割补将三角形转化为正方形和长方形等图形。我给予了学生十五分钟左右的课堂时间,学生发现了如下方法,将各边长长度一样的三角形拼凑为一个平行四边形或长方形,三角形的计算就转换为了求平行四边形的二分之一,例如底边长为四厘米,高为三厘米的三角形的面积为4×3÷2=6(cm2)。将三角形沿高剪开,得到两个各边长相等的三角形,并将其拼凑为一个平行四边形。学生根据结果得出结论,三角形面积计算公式为:三角形面积=底边长×高÷2,此时我提醒学生此三角形可能是个例,引导学生对其他三角形面积计算方法进行实践验算。学生经过验算得出以下结论:1.两个锐角三角形可合并为平行四边形;2.两个直角三角形可合并为长方形;3.两个等腰直角三角形可合并为正方形;4.两个钝角三角形可合并为长方形。
引导学生观察知识内容同异之处,通过实践验证知识概念的变化和性质,引导学生通过实践获取知识,达到利用求异思维锻炼学生思维能力目的的同时激发学生学习信心。
四、利用求异思维,改变思维模式
笔者认为利用求异思维可以有效帮助学生通过错误获得进步,面对学生出现的错误,教师不可无视,更不可过度批评打击学生自信心,教师可利用学生出现的错误,将其转换为引导学生思考的契机,帮助学生通过错误进行反思,并进行逆向思维的训练。
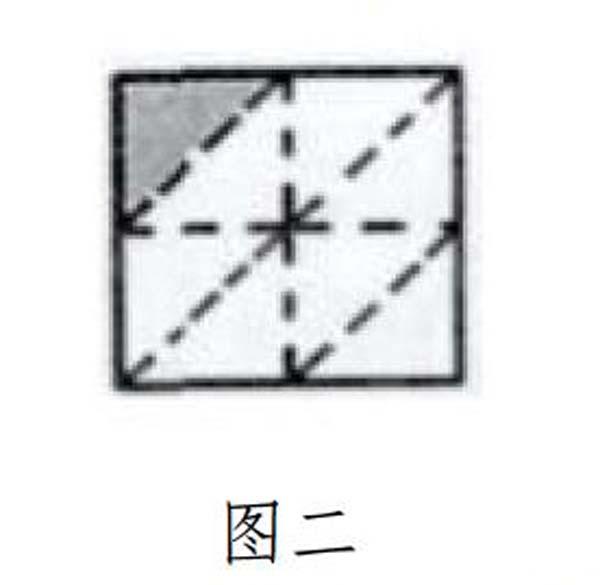
例如,在进行分数相关的教学工作时,我引导学生通过折纸表现1/2,1/4等分数。学生将长方形白纸沿中线直接对折,表现了1/2,而一位学生因为错误理解知识内容概念,出示图一,并表示自己折了1/4。此时笔者意识到可引导学生对该图片进行观察分析,并思考阴影部分是否可以表示1/4,学生思考后发现:此正方形虽然被分为了四份,不过每份面积并不相等,故不能用1/4表示,实际上,对该正方形再进行一次对折可以发现,图中阴影部分可表示1/8,如图二所示。
学生知识储备和思维能力相较于教师明显存在较大差距,故教师面对学生出现的错误,不应该过快得出结论,笔者认为引导学生根据错误原因进行深入思考可以有效强化教学效果,帮助学生通过多种角度、多种模式进行思考。
总之,小学数学教学工作中,教师可利用“求同”和“求异”思维帮助学生打造知识体系、培养创新思维、锻炼思维能力并形成多角度思考的思维模式。
【参考文献】
[1]王勇跃.浅谈小学数学教学中的“求同”与“求异”[J].小学教学参考,2019(17):39-40
[2]杨淑娟.小学数学教学中的“求异思维”[J].中小学教学研究,2013(05):30-31
(江苏省宿迁市宿豫区骏马小学,江苏 宿迁 223800)
