横轴流脱粒分离装置的数学模型的建立与试验
2020-08-27王勋威谢方平任述光王修善张正中
王勋威,谢方平,2,3*,任述光,2,3,王修善,3,张正中
横轴流脱粒分离装置的数学模型的建立与试验
王勋威1,谢方平1,2,3*,任述光1,2,3,王修善1,3,张正中1
(1.湖南农业大学机电工程学院,湖南 长沙 410128;2.南方粮油作物协同创新中心,湖南 长沙 410128;3.智能农机装备湖南省重点实验室,湖南 长沙 410128)
横轴流脱粒分离装置滚筒长度限制了其脱粒分离能力,仅被应用于中小型联合收割机。为研究横轴流脱粒分离装置脱粒滚筒转速、喂入量、脱粒间隙等因素对脱粒分离性能的影响,优化装置结构,利用概率学理论建立了横轴流脱粒分离装置的未脱净率和夹带损失率数学模型。对模型正确性验证试验表明,模型对未脱净率的预测相对误差为8.23%,对夹带损失率的预测相对误差为2.90%。仿真分析和试验表明,该模型可反映籽粒轴向分布和脱粒滚筒转速、喂入量、脱粒间隙等参数对脱粒分离性能的影响。
横轴流脱粒分离装置;数学模型;滚筒转速;喂入量;脱粒间隙
脱粒分离装置是联合收割机的核心部件,它直接影响整机的工作性能[1–3]。对脱粒分离过程进行理论分析,对于脱粒分离装置的优化设计至关重要。建立脱粒分离模型是深入研究脱粒分离理论的有效方法[4]。脱粒分离装置的数学模型研究有两类方法:一类是通过试验进行回归分析,得到回归模型;另一类则是对脱粒分离过程分析假设,推导构造数学模型。前者理论基础完善,应用广泛,但缺乏对脱粒分离过程本质的描述,对装置设计结构优化指导意义受到限制。HUYNH[5]提出了脱粒分离服从指数分布的概率模型,利用概率学理论建立脱粒分离数学模型的方法得到广泛认可。MIU等[6–8]建立了纵轴流脱粒分离装置的概率模型,并通过试验分析了滚筒转速、脱粒间隙、喂入量、作物含水率等因素对脱粒分离性能的影响。万金保等[9]导出了切流脱粒分离装置的脱粒分离概率模型,并建立了模型与装置结构参数、作物特性参数的数学关系,模型能反映实际脱粒分离过程。张金海等[10]分析了切流脱粒分离装置的脱粒分离过程,构造了概率模型的系数函数,并结合试验方法确定了模型系数,试验验证模型有较好的预测性能。李杰等[11]建立了纵轴流脱粒分离装置的概率模型,并用计算机进行模型曲线模拟,分析了籽粒沿滚筒轴向的分布规律。唐忠等[12]、李耀明等[13]建立了切流和纵轴流组合式脱粒分离装置的概率模型,并以此分析了不同脱粒元件的脱粒分离性能,为组合式脱粒分离装置数学模型建立提供了研究方法。这些研究对于不同结构形式的脱粒分离数学模型研究来说,模型与装置结构参数、作物特性的数学关系构造过于经验化。
小型联合收割机结构紧凑,均采用切向喂料的横轴流脱粒分离装置,MIU等[14]虽进行了切向喂料的轴流脱粒分离模型研究,与李耀明等[13]建立的复脱式横轴流脱粒分离模型方法相同,但对于喂入口处籽粒喂入位置对脱粒分离影响的处理有些简单化,且未分析模型中脱粒分离系数与装置结构参数和作物特性的关系。
笔者以4LZ–1.0型小型联合收割机脱粒分离装置[15]为研究对象,基于概率学理论,建立横轴流脱粒分离概率模型,分析籽粒的轴向分布规律及滚筒转速、脱粒间隙、喂入量等参数对脱粒分离损失形成的影响,以期改进脱粒分离装置结构,提升工作性能。
1 横轴流脱粒分离数学模型的建立
1.1 横轴流脱粒分离装置的工作过程
横轴流脱粒分离装置,其物料由辅助喂入轮从脱粒滚筒一端沿切向喂入,物料进入脱粒空间后迅速形成薄层,在脱粒滚筒和导向板的共同作用下,在脱粒空间内作螺旋运动[16–17]。与此同时,物料层受到打击、梳刷、搓擦、碾压等作用,籽粒从穗头脱落,完成脱粒过程。脱粒后的籽粒,不再受穗头连接力束缚,成为自由籽粒。自由籽粒在离心力作用下穿过物料层,到达凹板筛筛面,完成分离过程。由此可见,籽粒在脱粒空间内任意轴向长度位置处被脱粒或者分离是随机的,每个籽粒在喂入前状态是相同的,因而每粒籽粒在脱粒空间内某一位置处被脱粒或者分离的概率是相同的。脱粒装置的脱粒齿均匀分布,轴向脱粒间隙、滚筒转速相同;因此,可认为脱粒空间轴向任意位置处的脱粒能力相同,即在已知籽粒运动至轴向某一位置未被脱粒的前提下,在该位置被脱粒的概率相同,轴向位置距离喂入点距离越长,籽粒运动至该位置仍未被脱粒的概率越小。
1.2 脱粒分离模型的建立
为便于数学模型推导,以喂入口滚筒轴端点为原点,滚筒轴为轴,物料运动方向为轴正方向,物料喂入方向为轴正方向,建立坐标系,如图1所示。用轴坐标表示物料位于脱粒空间内轴向位置,研究脱粒分离过程的轴向分布。

图1 物料切向喂入轴流脱粒滚筒

()=1-e(1)
()=e(2)
同理,自由籽粒分离事件发生的概率分布函数()和概率密度函数()分别为:
()=1-e(3)
()=e(4)
式中:为脱粒系数;为分离系数。
为便于数学建模,作以下假设:1) 物料自喂料口喂入后立即进入脱粒空间进行脱粒,无物料反吐现象;2) 喂料口脱粒空间与其他区域脱粒分离能力相同;3) 在喂料口宽度区域内,物料能被均匀连续喂入。
根据假设3),可知籽粒喂入概率密度函数()服从均匀分布。
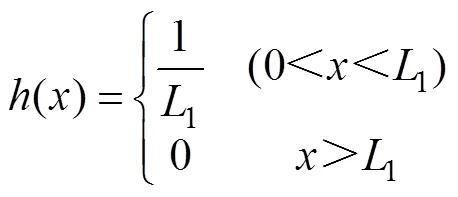
脱粒分离必须在喂入发生后进行,因此籽粒完成脱粒的概率密度函数1()为喂入概率密度函数()与脱粒概率密度函数()的卷积,其函数为分段函数。
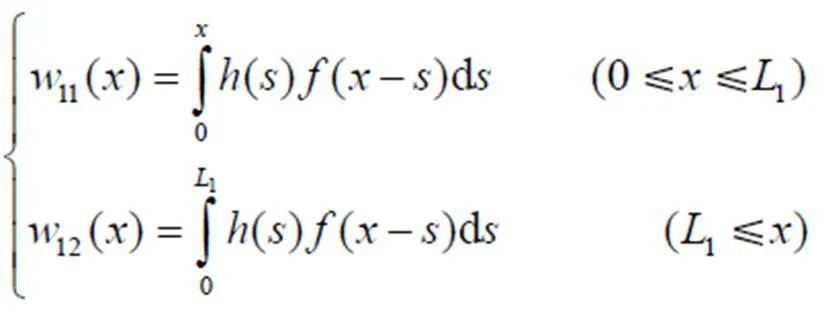

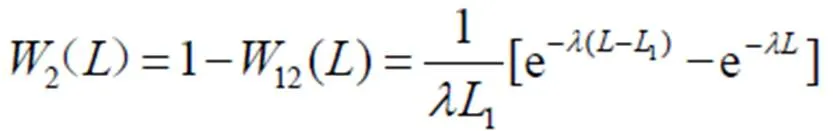

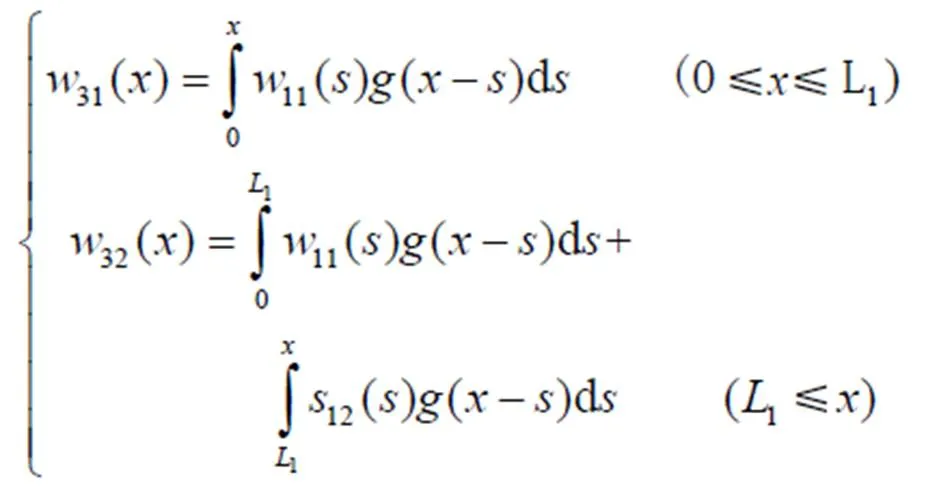
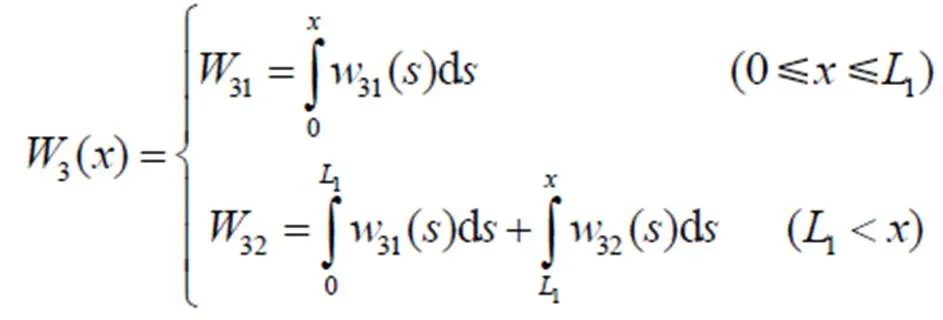
当时,3()即为脱粒分离装置的脱粒分离率。
在脱粒装置轴向处已完成脱粒未分离的自由籽粒函数为:
4()=1()-3() (11)
4()=1()-3() (12)
1.3 脱粒分离性能的影响因素
1.3.1脱粒系数函数构造
在钉齿式轴流脱粒分离装置中,籽粒主要因钉齿打击作用而脱粒,其次为物料与凹板筛搓擦作用脱粒。籽粒在脱粒空间内的打击次数和每次打击传递能量是影响打击脱粒性能的主要因素。
物料在脱粒空间内扫过的滚筒表面积与钉齿在滚筒表面的分布密度乘积即为物料受打击次数。物料相对滚筒表面扫过面积为1。
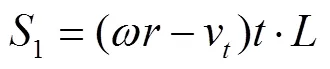
单个籽粒在脱粒空间内的当量打击次数


由碰撞理论可知,单个籽粒每次受打击吸收的能量:
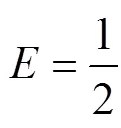
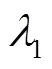
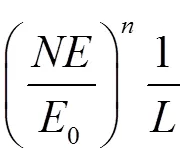
式中:k、为系数;0为单粒籽粒脱粒时克服穗头连接力所需的功。
搓擦作用脱粒主要依靠凹板筛和物料之间的摩擦作用脱粒,凹板筛与物料的摩擦作用越强,搓擦效果越好。摩擦力的大小与物料对凹板筛的压力有关。物料进入空间由蓬松状态厚度δ被压缩为脱粒间隙厚度,可假设每粒籽粒对凹板筛的当量压力P。

蓬松状态下物料厚度
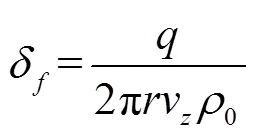
则单粒籽粒与凹板筛之间的摩擦力可表示为
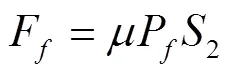
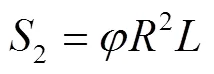
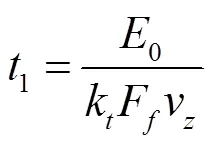
式中:v为物料轴向运动速度。
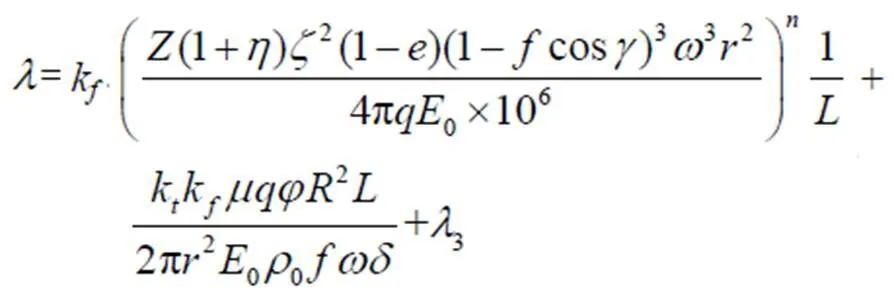
式中:为脱粒滚筒转速;为脱粒滚筒半径;为比例系数;为螺旋升角。
草谷比、籽粒千粒质量、籽粒恢复系数、单粒籽粒脱粒所需能量0等为物料特性,脱粒齿齿数、脱粒滚筒半径为脱粒分离装置的结构参数,物料与凹板筛之间的摩擦系数与凹板筛结构和物料特性均有关系。为研究脱粒滚筒转速、脱粒间隙、喂入量3个主要因素对脱粒分离性能的影响,将以上物理量均定为常数,对脱粒分离系数表达式进行化简,即得:

式中:1、2、、3均为待定系数。
1.3.2分离系数函数构造
假设籽粒在穿越物料层时所受外力恒定不变,籽粒在脱粒前受枝梗连接力约束沿滚筒径向受力平衡且无沿滚筒径向位移,脱粒后在离心力和重力作用下,在滚筒径向作初速度为0的匀加速运动。
籽粒穿越物料层的阻力与物料密度有关,物料密度越大,孔隙度越小,则籽粒受到的阻力越大。
实际分离过程并不是匀加速运动,且重力加速度在滚筒径向的分量和秸秆阻力产生的加速度也不恒定,因此用系数进行修正,求解分离过程匀加速运动的径向加速度a:
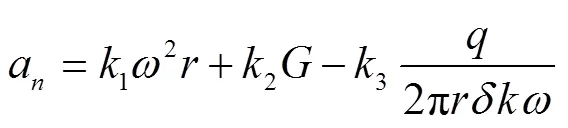
式中:1、2、3为修正系数;为重力加速度。

式中:0为常数,反映籽粒穿过物料层后凹板筛筛孔大小等因素对分离性能的影响。
滚筒转速、喂入量、脱粒间隙是影响脱粒分离性能的主要工作参数,仅考虑这些参数的影响,将脱粒滚筒半径和螺旋升角视为常数,对分离系数方程进行化简,则
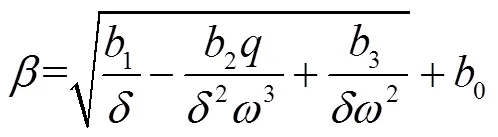
1.4 模型系数求解
已经建立的籽粒未脱净率、夹带损失率、脱粒分离率的数学模型中,脱粒分离系数值尚不确定,为确定取值,在4LZ–1.0型小型联合收割机上进行脱粒试验。试验水稻为Y两优900,测得籽粒含水率为21%,茎秆含水率为65%,籽粒千粒质量为26.65 g,草谷比为0.82。以喂入量、滚筒转速、脱粒间隙为影响因素,以未脱净率、夹带损失率为评价指标,按照正交试验设计方法,选取26组参数不同均匀分布的试验点进行试验,其中20组用于求解模型系数,其余均布的6组用于模型验证。
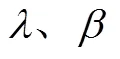
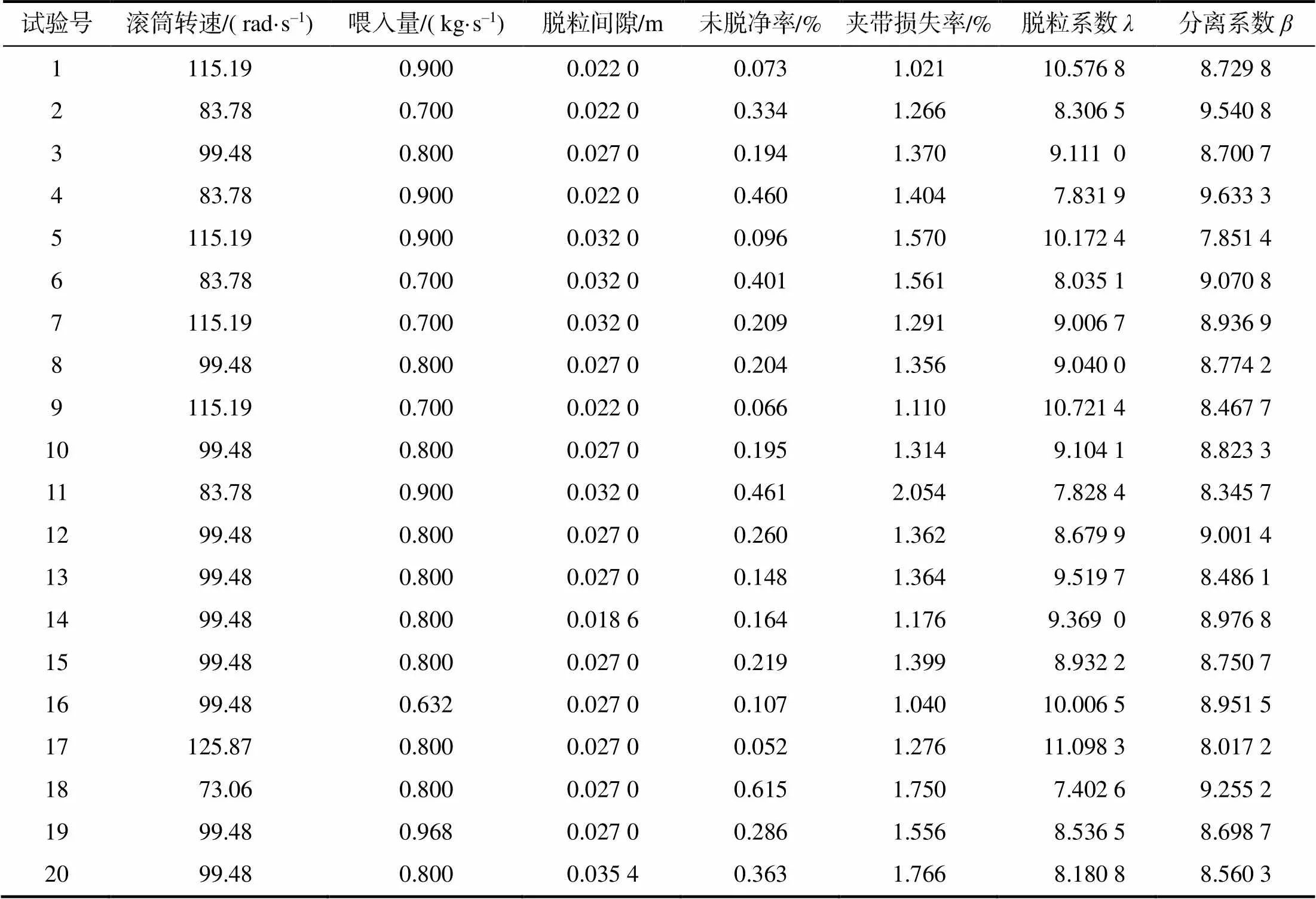
表1 脱粒系数分离系数计算值
使用非线性回归,求得脱粒系数模型式(22)和分离系数模型式(25)的系数:1=0.029 6,=0.388 4,2=4.088 3,3=0.895 6,1=0.023 5,2=1 458.409 4,3=2 201.542 4,0=5.997。
2 试验验证
为检验模型的准确性,用模型进行未脱净率和夹带损失率理论值计算,将理论值和实测值进行比较,判断模型的可靠性。对6个均匀试验点进行预测,对比结果如表2所示。

表2 验证试验的未脱净率和夹带损失率
经统计,未脱净率的相对误差均值为8.23%,夹带损失率的相对误差均值为2.90%。
3 模型应用
3.1 脱粒分离轴向分布
用Matlab绘制4LZ–1.0型小型联合收割机脱粒分离装置数学模型的仿真曲线,由表1的结果可知,脱粒系数∈[7.4,11.1],分离系数∈[7.8,9.6]。取=9.25、=8.7绘制未脱净籽粒率、自由籽粒率、累积脱粒分离率沿滚筒长度方向的分布曲线,结果如图2所示。

图2 切向喂料轴流脱粒分离模型的未脱净率、自由籽粒率、累计脱粒分离率
由图2可以看出,由于喂入口段物料均匀喂入,前端籽粒仅少量脱粒,随着喂入增加,累计脱粒分离量在喂入口段快速上升,随着脱粒分离过程的逐步完成,累计脱粒分离率趋近于100%;滚筒长度为[0.2,0.4],约50%的籽粒被脱粒分离。自由籽粒率与未脱净率均先增后减。由于籽粒分离过程在脱粒过程之后,自由籽粒率始终滞后于未脱净率,在滚筒末端值远大于未脱净率,因此,脱粒损失以夹带损失为主。
3.2 滚筒转速对未脱净率和夹带损失率的影响
滚筒转速是脱粒分离性能的显著影响因素,滚筒转速提高,可显著增强脱粒分离性能[18]。保持喂入量、脱粒间隙等不变,进行滚筒转速的单因素试验得到的结果如图3和图4所示。
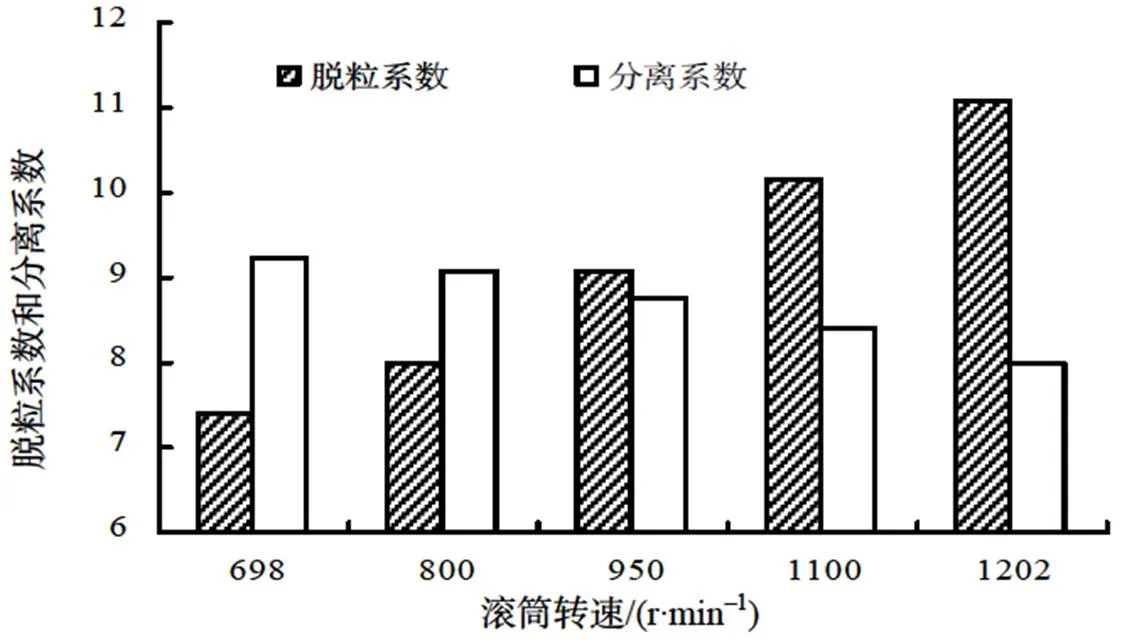
图3 不同滚筒转速的脱粒系数和分离系数
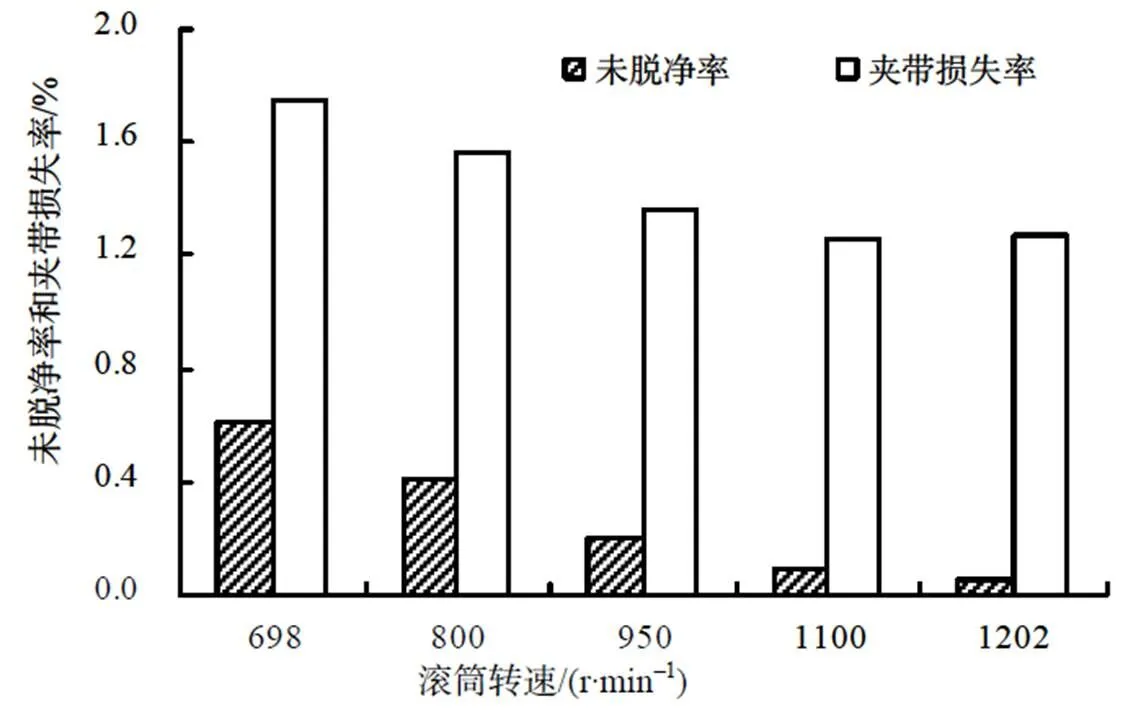
图4 不同滚筒转速的未脱净率和夹带损失率
随着滚筒转速的提高,未脱净损失和夹带损失均呈下降趋势,因此,可以通过适当提高滚筒转速来改善整机脱粒分离性能,但从脱粒系数和分离系数的变化来看,滚筒转速的提高仅仅改善了脱粒性能,分离性能反而有小幅下降。由此可见,滚筒转速提高后夹带损失减少是由于脱粒性能改善的缘故。转速提高,物料与脱粒滚筒间的相对运动速度也相应提高,物料受打击的频率也随之增加;因此,脱粒性能改善,籽粒在脱粒空间内脱粒提前,让籽粒有足够的时间分离,从而夹带损失减少。滚筒转速的提高,使物料在脱粒空间内的运动速度增加,籽粒的分离时间缩短,装置分离能力有小幅降低。脱粒转速的提高虽然可以减少脱粒损失,但是转速过高,打击力过大,将导致籽粒破损严重,且功耗增加。
3.3 喂入量对未脱净率和夹带损失率的影响
喂入量的单因素试验结果如图5、图6所示。未脱净率、夹带损失率随着喂入量增加均呈上升趋势,脱粒系数、分离系数也都相应降低。当喂入量增加,脱粒滚筒转速、脱粒齿齿数等参数一定时,总打击次数不变,则单粒籽粒受打击脱粒的概率降低,每粒籽粒获得的平均打击能量减少,因此脱粒性能下降。喂入量增加,使得脱粒空间内物料密度增加,物料层孔隙度减小,因此分离性能也有所下降。

图5 不同喂入量的脱粒系数和分离系数

图6 不同喂入量的未脱净率和夹带损失率
3.4 脱粒间隙对未脱净率和夹带损失率的影响
减少脱粒钉齿与凹板筛之间的间隙,可以使物料层变薄,钉齿作用于物料层的打击能量更容易传递至凹板侧,打击能量传递至凹板侧,凹板侧籽粒获得更多动能,籽粒与凹板的搓擦作用更强,也有助于脱粒。由式(18)可知,脱粒间隙减小,物料被压缩得更严重,对凹板筛的压力越大,有利于搓擦作用脱粒。从分离系数的表达式(25)可知,脱粒间隙减小,物料层密度增加,不利于分离;同时物料层变薄,减小了籽粒穿越物料层径向运动的距离,有助于分离。试验表明脱粒间隙减小,分离性能有所改善,仅说明在该试验条件下物料层厚度对分离的影响占主导地位,物料密度对分离影响较小(图7,图8)。因物料密度的变化与喂入量、滚筒转速也有关联,由式(25)可知,当喂入量、转速变化,脱粒间隙减小,并不一定使分离性得到改善。脱粒间隙减小,有助于脱粒,但是间隙过小,凹板筛对物料的搓擦作用过大,物料运动速度降低,物料与滚筒的相对运动速度增加,打击作用过强,导致籽粒破损增加。搓擦作用与打击作用增强也使功耗增加,当所需功耗过大,动力供应不足,将导致滚筒堵塞。
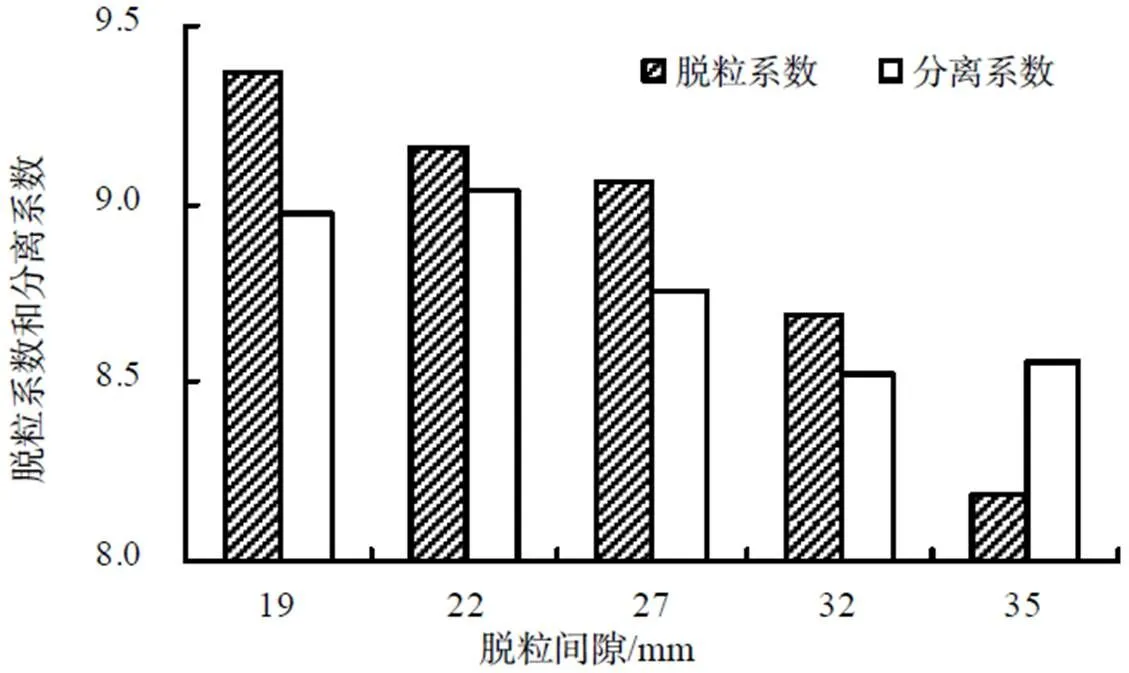
图7 不同脱粒间隙的脱粒系数和分离系数
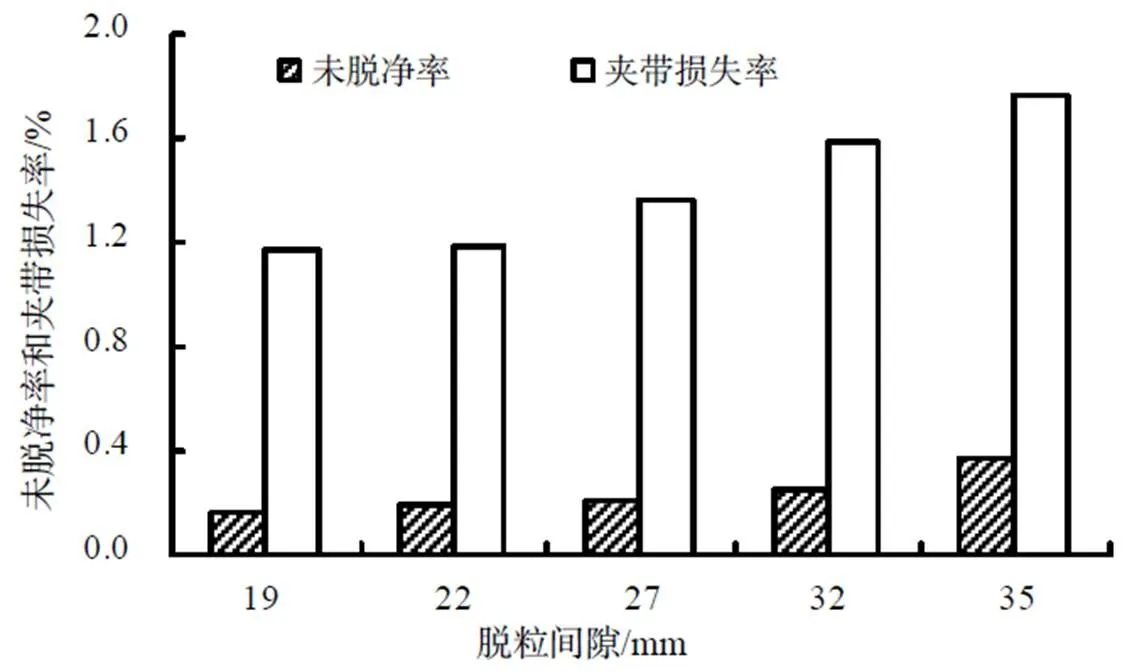
图8 不同脱粒间隙的夹带损失率和未脱净率
4 结论
通过分析滚筒转速、喂入量、脱粒间隙对脱粒分离性能的影响,建立了包含这些因素的切向喂料的横轴流脱粒分离装置数学模型。对模型正确性进行试验验证,分析模型理论值与试验实测值误差,未脱净损失率的平均相对误差为8.23%,夹带损失率的平均相对误差为2.90%。该模型可反映出未脱净率、自由籽粒量、累积脱净率在滚筒轴向的分布规律和滚筒转速、喂入量、脱粒间隙等参数对脱粒分离性能的影响。
[1] 张认成,桑正中.轴流脱粒空间谷物运动仿真研究[J].农业机械学报,2000,31(1):55–57. ZHANG R C,SANG Z Z.Simulation research on the motion of cereal in axial threshing space[J].Transactions of the Chinese Society for Agricultural Machinery,2000,31(1):55–57.
[2] 李耀明,李洪昌,徐立章,等.短纹杆–板齿式轴流脱粒分离装置性能试验[J].农业机械学报,2009,40(7):88–92. LI Y M,LI H C,XU L Z,et al.Performance test of short-rasp-bar of axial flow threshing and separating unit[J]. Transactions of the Chinese Society for Agricultural Machinery,2009,40(7):88–92.
[3] 钟挺,胡志超,顾峰玮,等.4LZ–1.0 Q型稻麦联合收获机脱粒清选部件试验与优化[J].农业机械学报,2012,43(10):76–81. ZHONG T,HU Z C,GU F W,et al.Optimization and experiment for threshing and cleaning parts of 4LZ-1.0 Q cereal combine harvester[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(10):76–81.
[4] 唐忠.切纵流结构谷物脱粒分离理论与试验研究[D].镇江:江苏大学,2013. TANG Z.Theoretical and experimental investigations of cereals threshing and separating on tangential- longitudinal axial device[D].Zhenjiang:Jiangsu University,2013.
[5] HUYN H M,POWELL V T,SIDDAL N J.Threshing and separating process-amathematical model[J]. Transactions of the ASAE,1982,25(1):65–73.
[6] MIUP I,KUTZBACH H-D.Modeling and simulation of grain threshing and separation in threshing units-Part I[J]. Computers and Electronics in Agriculture,2008(60):96–104.
[7] MIU P I,WACKE P,KUTZBACH H-D.A comprehensive simulation model of threshing and separating process in axial units Part I.Further model development[J]. AGENG Paper,1998,No AE98–A1–354.
[8] MIU P I,WACKE P,KUTZBACH H-D.A comprehensive simulation model of threshing and separating process in axial units.Part II.Model validation [J].AGENG Paper,1998,No AE98–A_475.
[9] 万金保,赵学笃,纪春千.传统型脱粒装置的数学模型及应用[J].农业机械学报,1990,21(2):21–29. WAN J B,ZHAO X D,JI C Q.A mathematical model for conventional grain threshing and it’s application[J]. Transactions of the Chinese Society for Agricultural Machinery,1990,21(2):21–29.
[10] 张金海,都丽萍.脱粒部件数学模型的建立与模拟[J].农业机械学报,1994,25(1):56–60. ZHANG J H,DU L P.Theoretical study of mathematical model on threshing and separating process[J]. Transactions of the Chinese Society for Agricultural Machinery,1994,25(1):56–60.
[11] 李杰,阎楚良,杨方飞.纵向轴流脱粒装置的理论模型与仿真[J].江苏大学学报(自然科学版),2006,27(4):299–302. LI J,YAN C L,YANG F F.Theoreticalmodel and simulation of threshing of axial unit with axial feeding[J]. Journal of Jiangsu University(Natural Science Edition),2006,27(4):299–302.
[12] TANG Z,LI Y M,XU L Z,et al.Modeling and design of a combined transverse and axial flow threshing unit for rice harvesters[J].Spanish Journal of Agricultural Research,2014,12(4):973–983.
[13] 李耀明,徐立章,邓玲黎,等.复脱分离装置的理论分析及试验[J].农业机械学报,2005,36(11):61–64. LI Y M,XU L Z,DENG L L,et al.Theoretical analysis and experimental study on rethreshingseparation unit[J]. Transactions of the Chinese Society for Agricultural Machinery,2005,36 (11):61–64.
[14] MIUP I,KUTZBACH H-D.Modeling and simulation of grain threshing and separation in threshing units-Part II. Application to tangential feeding[J].Computers and Electronics in Agriculture,2008(60):105–109.
[15] 谢方平,王修善,任述光,等.4LZ–0.8型小型水稻联合收割机的设计[J].湖南农业大学学报(自然科学版),2015,41(4):435–439. XIE F P,WANG X S,REN S G,et al.Design of 4LZ-0.8 type mini rice combined harvester[J].Journal of Hunan Agricultural University (Natural Sciences),2015,41(4):435–439.
[16] 衣淑娟,蒋恩臣.轴流脱粒与分离装置脱粒过程的高速摄像分析[J].农业机械学报,2008,39(5):52–55. YI S J,JIANG E C.High-speed photography analysis on process of threshing of axial flow threshing and separating installation[J].Transactions of the Chinese Society for Agricultural Machinery,2008,39(5):52–55.
[17] 杨方飞,阎楚良,杨炳南,等.联合收获机纵向轴流脱粒谷物运动仿真与试验[J].农业机械学报,2010,41(12):67–71. YANG F F,YAN C L,YANG B N,et al.Simulation and testing of cereal motion in threshing unit of combine harvester with axial feeding[J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(12):67–71.
[18] 康栋,吴崇友,梁苏宁,等.谷子联合收获机脱粒装置设计与试验[J].中国农业大学学报,2017,22(2):135–143. KANG D,WU C Y,LIANG S N,et al.Design and test of the threshing device of millet combine harvester[J]. Journal of China Agricultural University,2017,22(2):135–143.
A mathematical model and test of the horizontal axial flow threshing separation device
WANG Xunwei1, XIE Fangping1,2,3*, REN Shuguang1,2,3, WANG Xiushan1,3, ZHANG Zhengzhong1
(1.College of Mechanical and Electrical Engineering, Hunan Agricultural University, Changsha, Hunan 410128, China; 2.Collaborative Innovation Center of Southern Chinese Grain and Oilseed, Changsha, Hunan 410128, China; 3.Hunan Provincial Key Laboratory of Intelligent Agricultural Equipment, Changsha, Hunan 410128, China)
The cylinder length limits the threshing and separating ability of the horizontal axial flow threshing separation device, which is only used in the small and medium-sized combined harvesters. In order to study the effect of the cylinder speed, the feed rate and the concave clearance on the threshing performance of the horizontal flow threshing unit, a mathematical model was established to optimized its structure by using the probability theory.The verification tests were carried out, and the results showed that the average relative error of the prediction of the unthreshing rate is 8.23%, and the average relative error of the unseparated rate is 2.90%. Simulation analysis and single factor test showed that the model could reflect the influence of the threshing cylinder speed, the feed rate, the concave clearance and other parameters on the threshing separation performance.
horizontal axial flow; mathematical model; cylinder speed; feed rate; concave clearance

S225.3
A
1007-1032(2020)04-0480-08
10.13331/j.cnki.jhau.2020.04.016
王勋威,谢方平,任述光,王修善,张正中.横轴流脱粒分离装置的数学模型的建立与试验[J].湖南农业大学学报(自然科学版),2020,46(4):480–487.
WANG X W, XIE F P, REN S G, WANG X S, ZHANG Z Z. A mathematical model and test of the horizontal axial flow threshing separation device[J]. Journal of Hunan Agricultural University(Natural Sciences), 2020, 46(4): 480–487.
http://xb.hunau.edu.cn
2019–09–06
2020–03–08
国家自然科学基金项目(51175173);湖南省科学技术厅重点项目(2016NK2120)
王勋威(1993—),男,湖南衡阳人,硕士研究生,主要从事机械结构创新设计与试验研究,719269025@qq.com;
,谢方平,博士,教授,主要从事农业机械性能试验与创新设计研究,hunanxie2002@163.com
责任编辑:罗慧敏
英文编辑:吴志立
