基于多层热传导模型的高温专用服装研究
2020-08-27朱世昕李林蓉尚岩松郭秀锋
朱世昕 ,李林蓉 ,尚岩松 ,郭秀锋
(1.山西大同大学教育科学与技术学院,山西大同 037009;2.山西大同大学数学与统计学院,山西大同 037009)
对长期从事高温作业的人员,有必要采取有效措施对人体隔热,确保工作人员人身安全。服装作为高温防护的重要手段之一,在高温环境作业中备受关注,高温作业服装必须具备良好的防护性能、热湿舒适性能、工效性能以满足作业人员的需求。随着热防护技术的发展和对热防护要求的提高,热防护服不仅应具备较好的热防护性能和使用性能,还应具备良好的穿着舒适性。优良的热防护服既要对外界热量具有良好的阻隔作用,又要达到一定的热湿传递能力,以利于人体热量释放和汗液蒸发。但是,目前在热防护服和研究开发中,增强热防护性能与减少人体新陈代谢热负荷总是相互矛盾的,解决这一问题既是对科研工作者的挑战,又是一个机遇。
1 问题分析
(1)对环境温度为75℃、II 层厚度为6 mm、IV层厚度为5 mm,研究人皮肤外侧的温度分布。
首先建立合理的数学模型,选取合适的参数,计算出温度分布[1-3]。其次根据资料,分析研究各个参数代表的物理意义以及其运用,然后确定传热方式以及相关运算公式,最后根据已知参数构建合理的数学模型,确定各层温度与时间的函数关系。
(2)当环境温度为65℃、IV 层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60分钟时,不超过人体承受范围。
首先根据已知参数建立关于质量的目标函数,其次确定约束条件、运用最优化模型,最后使用Matlab 软件,得到65℃环境中,第II 层的最优厚度。
(3)当环境温度为80℃时,确定II 层和IV 层的最优厚度,确保工作30 分钟时,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过5分钟。
首先根据参数查阅相关模型资料,其次确定使用多层平壁的稳态导热模型确定各层温度与时间温度的函数关系,运用MATLAB 软件,分别得到第II层和第IV层温度与时间、厚度函数关系,从而确定80℃环境中II、IV层的最优厚度。
2 基本假设
专用服装材料各层之间及材料与假人皮肤外侧组成的系统衣物材料分别为Ⅰ层,Ⅱ层,Ⅲ层,织物与皮肤之间为Ⅳ层,如图1所示。

图1 材料层次关系图
1)热传导垂直于皮肤进行,故视为一维;
2)专用服装材料的三层织物材料各项同性;
3)热传导过程中专用服装材料织物结构几乎不变;
4)热传递仅考虑热传导,不考虑湿传递。
5)热传导到衣服上的过程是均匀的,假定织物材料没有发生溶解;
6)假人皮肤与专用服装材料之间距离微小,因而不考虑热对流。
3 模型建立与求解
3.1 环境75℃时,关于服装温度变化的研究
首先将数据按照时间间隔为200s 的依据进行筛选,根据所筛选的数据,运用MATLAB 绘制出拟合温度变化图,获得温度随时间的变化规律,如图2。
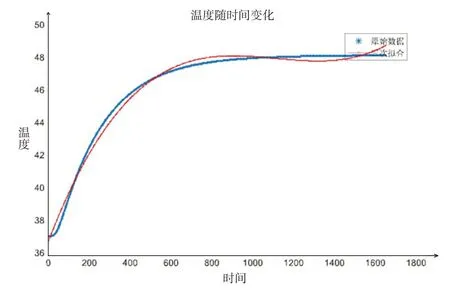
图2 皮肤温度与时间关系拟合图

其 中 :α1=9.0579e-9,α2=-3.0232e-5,α3=0.0325,α4=35.7243。
通过对问题一模型的求解,可以得到假人皮肤外侧温度随时间的变化,见表1。
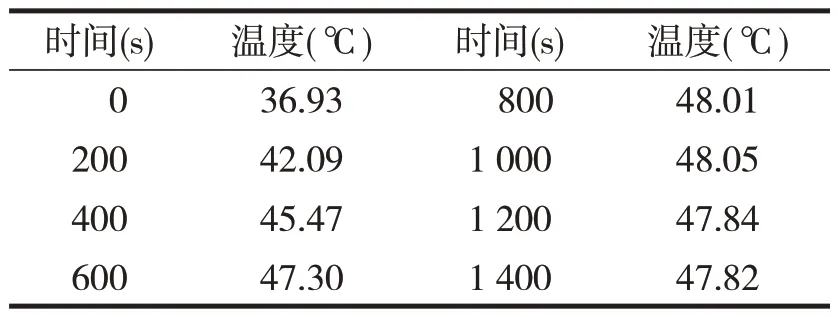
表1 假人皮肤外侧的测量温度
所得验证数据在误差范围之内,即所建模型正确。
3.2 环境65℃时,第二层最优厚度的研究
对于问题二来说,我们将Ⅰ,Ⅱ,Ⅲ层考虑为一个整体,将其看为一个多层平壁的稳态导热;并Ⅳ层考虑为一个整体,将其看为一个单层平壁的稳态导热,且二者之间的热量保持守恒,并不考虑各层之间的热对流,热辐射,湿传递等因素。根据热传导知识,运用热传导方程式,由傅里叶热流定律,得到一维平面热传导速率方程。由三个串联的热量传递环节所组成,其总热阻为:

且Ⅰ,Ⅱ,Ⅲ层总体的热流量为[4]:

图3 中,左侧为3 层,右侧为假人皮肤外表层,选取坐标轴x 与衣服面垂直,并建立单层平壁稳态导热数学模型[5-6]:
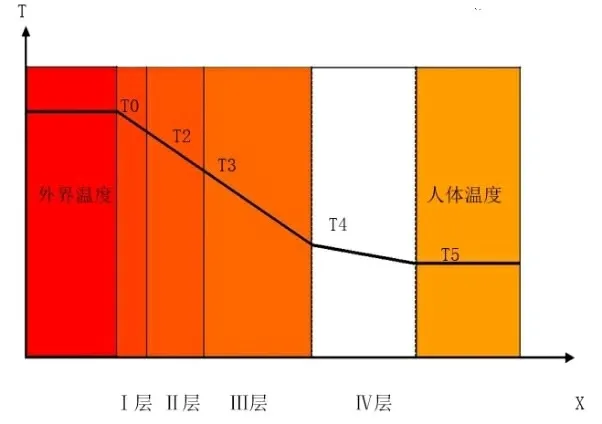
图3 单层平壁导热示意图

当X=0,T=Tm;X=H3,T=T4,
由傅里叶定律[4]得:

由多层平壁的稳态导热得:
Ⅰ层的热流量为:
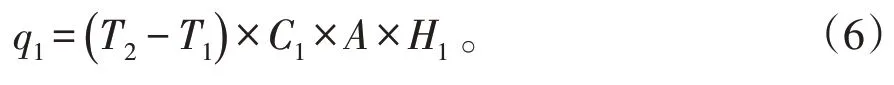
Ⅱ层的热流量为:

Ⅲ层的热流量为:
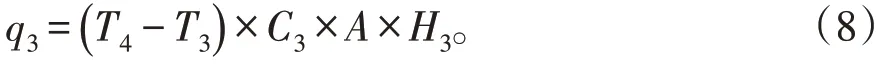
Ⅰ层的温度为[7]:

Ⅱ层的温度为:

Ⅲ层的温度为:

热流通过Ⅰ,Ⅱ,Ⅲ层的时间为:

且确保工作时间为60 分钟,假人皮肤外侧温度不超过47℃,且超过44℃的时间不超过五分钟:

求得第Ⅱ层的厚度范围为:[9.212,10.295]误差小于10-3,选取9.212 为第二层最优厚度,即:H2=9.212。
3.3 环境80℃时,确定类似Ⅱ和Ⅳ层的最优厚度
根据上述模型,结合t1+t2+t3=30 min,
且确保工作时间为60 分钟,假人皮肤外侧温度不超过47℃,且超过44℃的时间5 分钟:
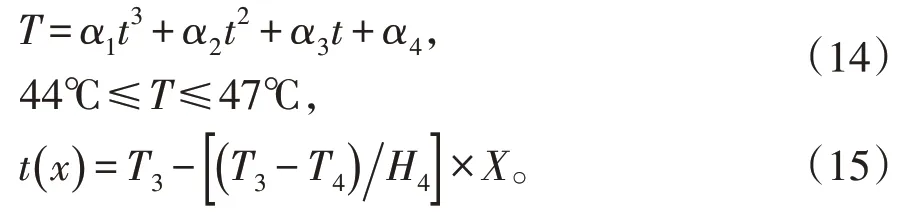
通过计算,Ⅱ层的最佳厚度范围为:[11.686,13.806],Ⅳ层的最佳厚度范围:[5.264,6.218],误差小于10-3,满足了我们的需求,所以选取11.686和5.264 作为Ⅱ,Ⅳ层的厚度。
4 结论
高温服装作为高温防护的重要手段之一,在高温环境作业中备受关注,对此我们进行了研究,通过观察假人外侧皮肤温度,建立温度随时间变化的模型并用MATLAB软件做出拟合函数和plotfit曲线图像,进行非线性问题求解,由温度随时间的变化反解出最优厚度,从而发现了在温度为75℃下,作业服能够满足作业人员的要求,并且在持续5 分钟,依旧能保持很好的热防护性能,但是我们仅考虑了服装层之间的热传导,而不考虑空气湿传递和热辐射,会缺失最优解,将环境条件理想化,致使有些问题边界考虑不全面。
