基于自适应代理模型的结构动力可靠度分析方法

石岩，陈晓岚，刘炜，李昕

(1.西北工业大学 航空学院， 西安 710072)(2.北京电子工程总体研究所 结构与强度总体研究室， 北京 100854)

0 引 言

结构动力可靠度分析能够衡量结构在动态载荷激励下的安全状态，对于评价结构的工作性能具有重要的指导意义。对于在随机过程激励下的动力可靠度分析问题，传统的分析方法往往仅考虑动态激励载荷的随机性而忽略了材料力学性能参数的随机性。而对于实际的工程结构，由于制造、工艺等的不确定性通常会导致材料力学性能参数也具有不确定性。因此，建立能够同时考虑动态激励载荷随机性和材料力学性能参数随机性的动力可靠度分析方法对于准确度量结构的安全程度具有重要的价值。

同时考虑动态激励载荷随机性和材料力学性能参数随机性的动力可靠度分析已经受到了越来越多研究者的重视，并且相关研究已经取得了一定成果。陈颖等[1]仿照随机变量响应函数模式建立了结构动力可靠度分析的响应函数，并引用序列响应面法来对响应函数进行拟合，从而将耗时的有限元模型调用转化为确定的显式功能函数的可靠性计算问题；陈建兵等[2]建立了一种不需要计算跨越率的概率密度演化方法来计算随机振动的可靠度，所提方法同时具有较高精度且能够在一定程度上减小计算成本；乔红威等[3]通过分裂法[4]将多维动力可靠度响应函数转换为一维问题，并使用Hermite多项式来近似单随机变量的动力可靠度响应函数，最后结合数值模拟方法来对随机激励下的动力可靠度进行求解；谭平等[5]提出使用Gauss-legendre积分公式来将随机结构地震激励下的无条件动力可靠度的复杂积分问题转化为积分点加权求和的形式进行求解，提高了计算效率；杨英杰[6]利用概率密度演化理论进行随机激励下非线性框架结构的动力响应以及可靠度分析，并考察了计算过程中有限差分步长和响应量区间长度对可靠度分析的影响。以上这些方法在计算最终的动力可靠度时均使用了基于数值积分或点估计的计算过程，而这个过程不可避免地会引入计算误差。

基于自适应Kriging代理模型[7]的可靠性分析方法近年来受到了越来越多的关注。相比于通过给定样本直接构建代理模型而言，自适应的代理模型能够根据需要自主地筛选出对设定目标贡献最大的样本点，从而能够使用尽可能少的样本点来获得较好的代理结果。B.Echard等[8]根据Kriging代理的预测均值和方差，构建出U学习函数来对结构功能函数的极限状态面进行高效预测；B.J.Bichon等[9]通过构建期望可行性函数(EFF)来对结构功能函数进行代理，所构建的EFF同时考虑了样本点与极限状态面之间的距离以及预测样本的变异性；Sun Z L等[10]提出最小提高函数(LIF)来衡量新训练样本点的加入对失效概率的贡献大小。若使用Kriging代理模型方法来对动力可靠度进行计算，其构建的为材料力学性能参数与条件动力可靠度之间的代理模型，而最终的动力可靠度为条件动力可靠度的均值。以上学习函数的本质在于将功能函数的极限状态面代理准确，而非代理模型输出的均值。因此，以上学习函数均不能直接用来构建自适应的Kriging模型对动力可靠度进行计算。

陶瓷基复合材料具有轻质性、高强韧性、抗氧化等优异特性，因此将该材料应用于航空发动机、飞行器机翼等结构上能够极大地减轻结构的重量，提高其性能。近年以来，基于陶瓷基复合材料的结构设计制造已经成为研究重点[11-14]。

本文研究C/SiC陶瓷基复合材料蒙皮骨架结构在承受随机振动载荷环境下的动力可靠度分析问题。结合基于马尔科夫过程假设[15-16]的动力可靠度计算公式，构建材料力学性能参数与条件动力可靠度之间的Kriging代理模型；基于Kriging模型推导计算动力可靠度的解析表达式；提出一个新的学习函数构建自适应的Kriging代理模型，并进行可靠度分析计算。

1 结构动力可靠度分析

一般情况下，可将结构在动态载荷作用下的动力响应表达为y(t)。结构的动力可靠度RT定义为动力响应y(t)绝对值在时间区间[0,T]内不超过安全界限值ε的概率，即

RT=P{|y(t)|≤ε,∀t∈[0,T]}

(1)

在通过首次超越理论计算结构的动力可靠度RT时，基于假定动力响应y(t)与安全界限的交叉次数服从马尔科夫过程可得到动力可靠度计算公式：

(2)

(3)

式中：Syy(ω)为动力响应y(t)的自功率谱密度函数。

本文针对在随机振动载荷和随机材料力学性能参数作用下的C/SiC陶瓷基复合材料蒙皮骨架结构的动力可靠度进行求解，其中随机振动载荷以PSD的形式进行加载。在通过有限元软件进行模型的不确定性分析时，可直接输出动力响应y(t)的自功率谱密度函数Syy(ω)。

2 考虑材料力学性能参数不确定性动力可靠度高效算法

直接使用上一节中给出的公式计算结构的动力可靠度时无法考虑材料力学性能参数的不确定性。在此使用X=[X1,X2,…,Xn]和x=[x1,x2,…,xn]分别表示需要考虑的具有随机不确定性的n维材料力学性能参数向量及其实现值，则上一节中给出的计算公式仅仅能计算出在给定材料力学性能参数实现值x下的动力可靠度结果，记其结果为RT(x)。则同时考虑载荷随机性和材料力学性能参数随机性的动力可靠度RTX可计算为

(4)

式中:fX(x)为材料力学性能参数向量X的联合概率密度函数。

式(4)为n维积分问题，由于在材料力学性能参数实现值x与动力可靠度RT(x)之间往往不具有显式关系，因此解析求解公式(4)显得尤为困难。求解上式的传统方法为Monte Carlo(MC)模拟法，该方法通过抽取材料力学性能参数向量X的大量样本，并计算在每一样本下的条件动力可靠度结果，最终通过求解所有条件动力可靠度结果的均值来获得RTX的结果。在抽取的材料力学性能参数样本足够大的情况下，该方法能够获得精确的动力可靠度RTX的结果。但是该方法需要大量的调用有限元分析软件，因此其计算效率较低，在工程上往往不可行。为了提高计算效率，可通过各种点估计方法如稀疏网格法[17]产生少量样本点来计算动力可靠度RTX。由于稀疏网格法是一种能够同时兼顾计算精度和效率的高效点估计方法，本文以稀疏网格法计算得到的动力可靠度结果作为对照解。

2.1 基于Kriging模型的动力可靠度解析表达

(5)

cov(x(i),x(j))=σ2Rθ(x(i),x(j))

(6)

式中：x(i)和x(j)为不确定材料力学性能参数向量X的任意两个实现值；σ2和Rθ(x(i),x(j))分别为稳态高斯过程z(X)的方差和相关函数。

本文使用如下的相关函数：

(7)

式中：θk(k=1,2,…,n)为参数。

(8)

(9)

式中：F为回归矩阵，其元素为Fij=hj(x*(i))(i=1,2,…,m;j=1,2,…,n)；R为相关矩阵，其元素为Rij=Rθ(x*(i),x*(j))(i,j=1,2,…,m)。

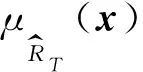
(10)

σ2[1-rT(x)R-1r(x)+uT(x)(FTR-1F)-1u(x)]

(11)

式中：r(x)=[Rθ(x,x*(1)),Rθ(x,x*(2)),…,Rθ(x,x*(m))]T且u(x)=FTR-1r(x)-h(x)。

一般情况下，在获得条件动力可靠度RT(X)代理模型后，需要将其结合式(4)使用数值积分等方法来计算最终的动力可靠度RTX。虽然此时已不需要调用真实有限元分析软件进行计算，但是由于使用数值积分，这个过程往往会引入新的计算误差。为了避免由于使用数值积分所导致的计算误差，本文基于Kriging模型，推导出计算动力可靠度RTX的解析表达式。将条件动力可靠度RT(X)的Kriging预测均值代入式(4)，得到动力可靠度RTX的计算式：

RTX

(12)

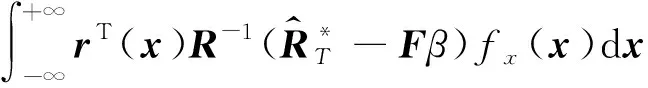
(13)

在此使用0阶回归多项式，其对应的回归模型h(X)=1，此时回归参数为β。并将r(x)的表达代入上式，将RTX表达为

(14)

式中：Rθ(x,x*(i))(i=1,2,…,m)由式(7)进行求解。

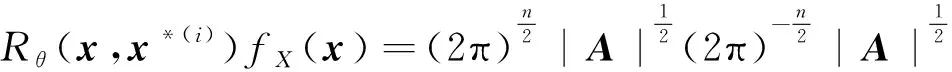
(15)

式中：

(16)

式中：

(17)

(18)

式(18)中所有输入量均为在构建代理模型时可以得到，因此动力可靠度RTX可以通过上式便捷地进行求解。同时，通过该解析表达式对动力可靠度RTX进行求解可以避免使用数值积分时引入的计算误差。

2.2 新学习函数

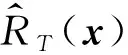
(4) 挑选出的新训练样本点与已有训练样本点之间不应过于聚集，否则易导致代理模型在局部具有较高的预测精度而在全局预测精度较差，这对于RTX的计算精度有较大影响。

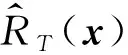
(19)

(20)

同时可求得V(x)的均值μV(x)为[20]

(21)

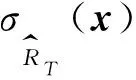
(22)

Lmin(x(i))=min {Li1,Li2,…,Lim}

(23)

使用Lmin(x(i))避免训练样本点之间过于聚集的问题。

基于以上分析，可构建针对样本池中第i个样本x(i)的学习函数表达式：

(24)

则能够使学习函数M(x(i))最大化的样本池中样本点x(i)(i=1,2,…,N)需要被筛选出来更新Kriging代理模型，即新的训练样本点x*(new)通过式(25)挑选：

(25)

由于动力可靠度RTX事先不知道，因此本文在计算μV(x(i))时均使用当前的Kriging代理结合推导出的动力可靠度RTX计算公式(18)进行求解。

2.3 自适应代理过程求解动力可靠度

将自适应Kriging代理模型方法结合所提出的新学习函数来计算动力可靠度RTX的计算步骤总结如下：

步骤1：使用材料力学性能参数向量X的联合概率密度函数fX(x)产生N组样本x=(x(1),x(2),…,x(N))作为样本池，并随机抽选出m组样本作为初始训练样本集x*=(x*(1),x*(2),…,x*(m))，结合式(2)计算相应的条件动力可靠度结果。

步骤2：使用当前的训练样本集x*=(x*(1),x*(2),…,x*(m))和相应的条件动力可靠度结果构建Kriging代理模型。

步骤3：使用当前的Kriging代理模型对样本池中的样本x=(x(1),x(2),…,x(N))进行预测，并使用解析公式(18)计算动力可靠度RTX的结果。如果连续两次计算得到的动力可靠度RTX相对误差小于10-4，输出当前的RTX作为动力可靠度结果。否则，使用式(24)计算样本池中样本x=(x(1),x(2),…,x(N))对应的学习函数的结果M(x(i))(i=1,2,…,N)。

步骤4：使用式(25)计算新的训练样本点x*(new)并将其添加入训练集，结合式(2)计算在该样本下的条件动力可靠度结果，令m=m+1并返回步骤2。

3 蒙皮骨架结构动力可靠度计算

飞机蒙皮骨架结构为飞机机翼典型构型件，研究飞机蒙皮骨架结构在随机振动载荷下的动力可靠度分析问题对于评估飞机机翼的整体安全性能具有一定指导意义。在此通过本文提出的高效方法对飞机蒙皮骨架结构在随机振动载荷以及随机材料力学性能参数共同作用下的动力可靠度进行计算分析。简化的蒙皮骨架结构的尺寸如图1所示。

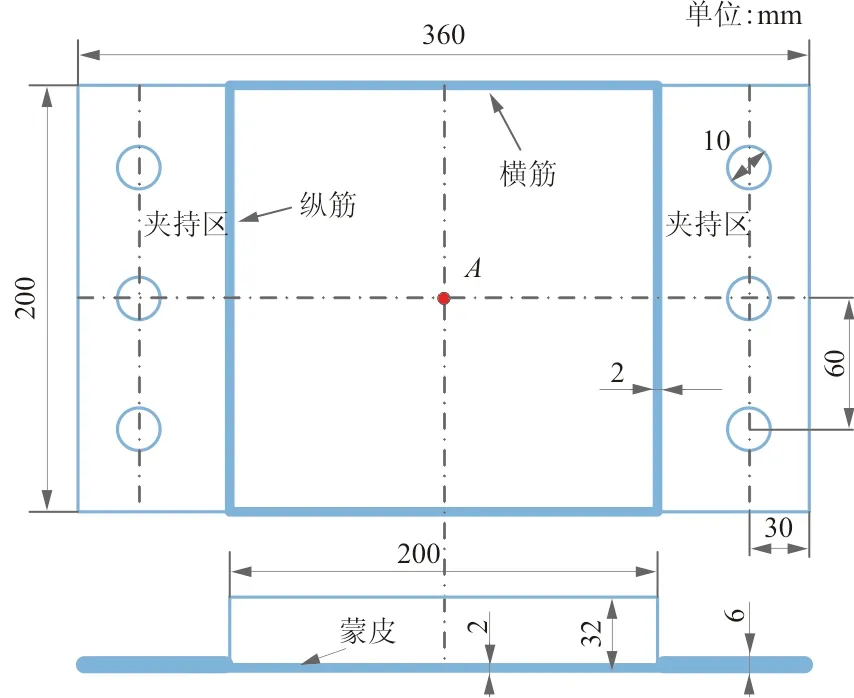
图1 飞机蒙皮骨架结构尺寸

蒙皮骨架结构承受的随机振动载荷以加速度功率谱密度的形式进行加载如图2所示，持续时间为3 min。

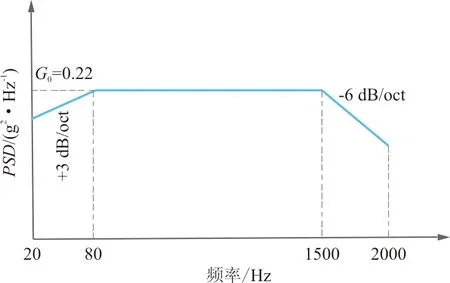
图2 随机振动功率谱密度

具有随机不确定性的材料力学性能参数包括C/SiC复合材料弹性模量E1和E2(其中1和2分别表示复合材料的两个方向)，泊松比υ，面内剪切模量G12、G13和G23，密度ρ以及结构的阻尼比γ。由于复合材料属性导致E1=E2，G13=G23。本文假定各个材料力学性能参数的分布类型及分布参数如表1所示，其中γ的变异系数为0.03，其余参数的变异系数为0.05。

表1 输入材料力学性能参数分布类型及分布参数

使用Abaqus 15.0对图1所示的飞机蒙皮骨架结构进行建模，以蒙皮中点(图1所示A点)在垂直于蒙皮方向(沿z轴)的位移超过指定值ε定义为结构失效。C/SiC复合材料的铺层结果如图3所示，复合材料按照0°和90°方向交替铺设，单层厚度0.2 mm，夹持区铺设30层，其他部分铺设10层。

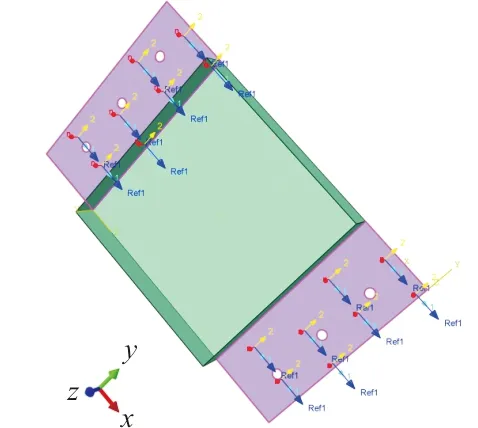
(a) 夹持区

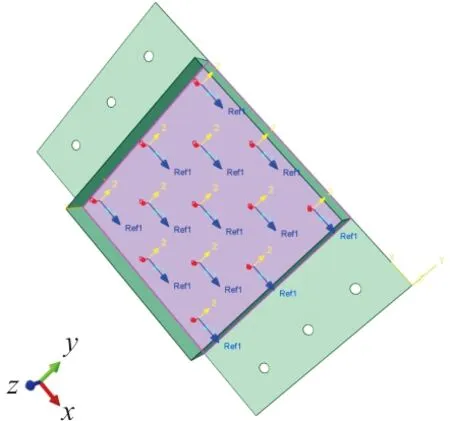
(b) 蒙皮

(c) 横筋

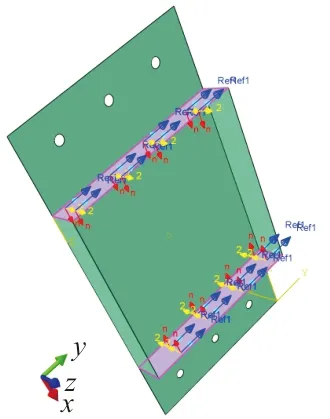
(d) 纵筋

蒙皮骨架结构前四阶模态如图4所示，其中U3表示沿z轴的位移。

(a) 1阶模态

(b) 2阶模态

(c) 3阶模态

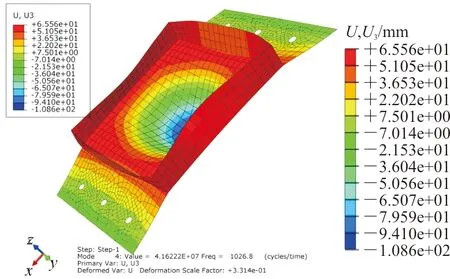
(d) 4阶模态

从图4可以看出：蒙皮骨架结构的前四阶模态对应的频率分别为440.10，744.24，918.13和1 026.8 Hz。

在材料力学性能参数均值处A点沿z轴位移的功率谱密度曲线如图5所示，可以看出：在如图2所示的功率谱密度振动载荷作用下，对该蒙皮骨架结构影响较大的为其前四阶模态所确定的频率范围；且在1阶模态对应的频率处，该蒙皮骨架结构的响应功率谱密度具有最大值，说明1阶模态对振动载荷的响应起主要作用。

图5 在材料力学性能参数均值处A点沿z轴位移PSD曲线

不同阈值下的动力可靠度计算结果如表2所示，其中SP为稀疏网格方法；MC为Monte Carlo模拟方法；Kriging为本文提方法；Ncall为调用有限元模型进行分析的次数。

表2 动力可靠度计算结果

从表2可以看出：所提自适应Kriging代理方法具有较高的计算精度，同时能够极大的减少计算成本；所提的自适应Kriging代理模型方法的计算效率高于基于稀疏网格技术的方法，且随着给定阈值ε的提高，自适应Kriging代理模型方法的计算量减小，而基于稀疏网格技术的方法计算量保持为恒定值。

在ε=0.23时，提出的自适应Kriging代理方法与非自适应Kriging代理方法计算出的动力可靠度的收敛图如图6所示。

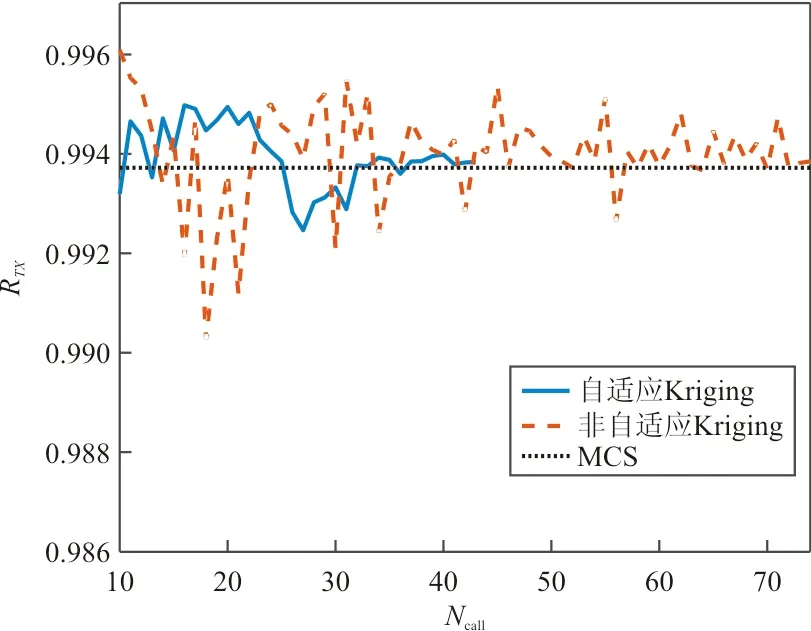
图6 动力可靠度计算结果随计算量变化图

从图6可以看出：通过结合本文所提新的学习函数来构建自适应的Kriging代理模型，可以极大地减小计算成本，提高收敛速度，同时结果具有较大精度。

4 结 论

(1) 本文采用了一种能够同时考虑载荷随机性和材料力学性能参数随机性的动力可靠度计算新方法，通过构建的Kriging代理模型推导出了动力可靠度的解析表达式，避免了由于基于Kriging模型使用数值积分方法对动力可靠度进行求解时所引入的计算误差。

(2) 提出了一种新的学习函数来筛选对计算动力可靠度有较大贡献的新训练样本点，所提学习函数同时考虑了预测值与动力可靠度的差异，预测值的标准差、预测样本的密度和其与已有训练样本点之间的距离。基于所提学习函数，可以构建自适应的Kriging代理模型过程，从而能够使用尽可能少的计算成本获得准确的动力可靠度计算结果。

(3) 通过飞机蒙皮骨架结构在振动载荷作用下的动力可靠度分析结果可以看出，所提高效方法不仅具有较高的计算精度，同时能够极大地减少计算量，节约计算成本。