考虑玛琳斯效应下聚氨酯缓冲块有限元分析
2020-08-26段峰张朝辉邬建海程李
段峰 张朝辉 邬建海 程李
上海众力投资发展有限公司,中国·上海 201506
对聚氨酯材料进行了试样的基本拉伸和压缩测试以及应力软化现象的测试,利用ABAQUS软件提供的模型,拟合处理所需材料本构常量,并建立了有限元模型,获取到了包含损伤在内的刚度曲线。通过实验测试出了材料的永久变形与材料应变等级的关系,利用这一关系修正了有限元分析结果。通过测试与有限元结果的对比,验证了有限元分析方法的合理性。
ABAQUS;聚氨酯缓冲块;泡沫橡胶;有限元分析;玛琳斯效应
1 引言
减震器在大载荷下时,为了防止减震部件之间发生干涉、“穿刺”的风险,在减震系统主承载单元(减震器、螺旋弹簧等)中加入缓冲元件,这种元件即为缓冲块,要求它具有抗冲击、抗耐磨以及高非线性的特点。
发泡多孔聚氨酯材料具有良好的机械性能,非线性特性,低泊松比,高承载、抗张力和抗撕裂能以及优良的耐磨性能,这些特性能很好的适应缓冲块的工作状态,现代减震器缓冲部件有90%以上的材料在使用聚氨酯材料。
有限元技术已经广泛应用于聚氨酯结构的设计与分析,但由于聚氨酯材料具有超弹性特点,在受载过程中随着应变等级的增加其力学性能存在软化现象,这一现象被称为玛琳斯效应。玛琳斯效应会导致不同类型的缓冲块在不同载荷下的损伤存在大的差异,这使得仿真精度的降低,增加了分析中的不确定性因素。论文通过利用单轴拉伸和压缩的方式获取聚氨酯材料本构关系,同时获取材料的软化特性,利用ABAQUS提供的本构关系建立了有限元分析模型,在一定程度上提高了分析精度[1]。
2 聚氨酯材料本构关系及分析
发泡聚氨酯为泡沫多孔材料,且多为受压状态,材料的压缩可分为三个阶段,分别为:第一阶段,应变在小于5%时,孔隙并未相互作用,此时表现为线弹性特性;第二阶段,随着应变的增大,聚氨酯空隙受压相互作用,孔隙发生屈曲从而进入屈曲变形区;第三阶段,所有孔隙受压变形后,产生相互挤压变形,从而进入了质密区,产生最大模量,极限压缩应变范围为70%~90%。发泡聚氨酯力学特性如图1所示,随着应变的不断增加,力学性能也随之变化。

图1 发泡聚氨酯典型压缩实验
在ABAQUS中,泡沫橡胶模型Hyperfoam是基于OGEN模型所定义的应变能函数,它能对超弹性高度压缩情况下进行有效的模拟。通过以下应变能函数定义其弹性行为:

其中,N为阶数,根据材料模型定义;μ、α和β为温度相关的材料参数;λi为主伸长比;Jel为弹性体积率,与主伸长相关;Jel=λ1λ2λ3;βi决定了材料的压缩性能,其与泊松比νi有关;βi=νi/(1-2νi),如果在各组应变能中,存在同一个βi,则泊松比为唯一的记作ν。

图2 聚氨酯试样实验转置
试样采用直径为30mm,高度为40mm的圆柱试样进行实验,如图2(a)所示进行安装,采用电子静态试验机进行往复加载,每一种载荷下往复次数为4次。随着加载载荷的变化,每次加载-卸载循环中材料均会发生损伤,其加载与卸载所围成的面积即为能量损耗值,损伤量的大小随着应变的增大而累积发生;同一应变作用下循环损伤完成后不再累积;将每一次应变增大的第一次加载曲线相连即为无损伤(初始加载曲线)下的加载曲线。从曲线上看,随着应变等级的增大其损伤逐渐增大的现象称为玛琳斯效应,这一效应的产生会使不同应变下产生大的应力偏移。随着载荷的重复,力学性能也趋于稳定,到一定程度后总损伤不再发生变化,此时可反应出材料的力学特征。由于损伤累积会导致后续的应变等级的应变无法从0点开始或回到0,此时,材料即发生了塑性永久变形,根据多次测试分析认为,不同的材料存在极为接近的永久变形,可以测试出不同材料随着应变等级变化的永久变形状态,由于在Hyperfoam中未包含永久变形的定义,实验出合理的永久变形,对后续数据修正能提供较大的帮助[2]。

图3 发泡聚氨酯损伤曲线
通过引入R.W.Ogden和D.G.Roxburth模型建立能量耗散关系,如式2所示

其中r、m和β为材料常数。
利用哑铃试样拉伸如图2(b)和圆形试住的压缩实验如图2(a)所示设备配合光学视频引伸计对应变和应力进行采集,获取发泡聚氨酯典型拉伸压缩曲线以及损伤曲线,用ABAQUS建立材料模型,拟合基本力学模型中的材料常数mu1、alphal和nu1;用损伤模型拟合出损伤模型的材料常数r,m和Beta[3]。
对试样进行不同应变等级下的压缩实验,得到永久应变与应变等级之间的关系曲线,并利用多项式方程建立方程如式3所示,通过代入应变等级即可求出此聚氨酯材料相关的永久应变。

其中εp永久应变与试样高度有关,εr为应变等级。
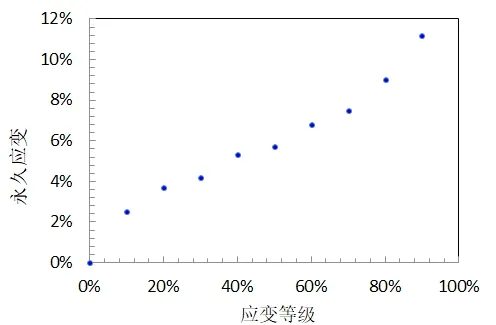
图4 试样永久变形与应变等级关系
由于缓冲块为轴对称结构,在分析时采用轴对称的方式建立仿真模型如图4所示,计算采用ABAQUS 隐式求解器进行求解,模型中使用CAX4H单元类型进行超弹性本构的模拟。通过刚体单元来模拟聚氨酯缓冲块与减震器其它金属部件的连接关系,下刚体约束全部自由度,上刚体施加向下载荷,并定义载荷循环幅值曲线,模拟加载与卸载过程,其计算的加载与卸载结果如图5所示。
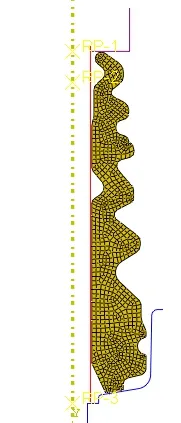
图5 缓冲块有限元模型
3 聚氨酯缓冲块压缩实验
利用INSTRON静态测试仪对缓冲块进行静刚度曲线测试,提取安装缓冲块在减震器总成中的边界,制作仿形工装,将缓冲块安装固定于工装中,设备作动端与工装活动部分连接,安装如图6所示。按照JIS K 6385 执行测试,动作端以10mm/min的速度施加载荷,循环加载4次,取最后一次数据作为缓冲块静态性能结果,包含了加载曲线和卸载曲线,第四次后损伤不再增加(再次施加循环载荷时,其加卸载曲线将与图7所示的曲线重合),因此第四次加载可以反应聚氨酯缓冲块的稳定性能。

图6 缓冲块卸载和加载有限元结果

图7 第四次加载循环曲线图
4 实验与分析与对比
仿真结果如图8所示,图中可以看出不同位移载荷下的加载曲线保持一致,应变等级不同导致卸载曲线与总损伤均存在差异,另外不同应变等级下材料产生的永久变形也不同,如图9所示,图8分析结果中并未体现永久变形的影响,因此需要通过材料的永久变形状态来调整分析结果的位移结果[4]。

图8 缓冲块测试安装
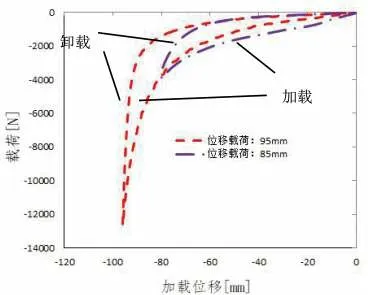
图9 不同位移载荷下的分析结果

图10 测试与分析结果对比
如图8所示,相关分析结果表明,通过分析模拟材料的随着应变等级的变化其软化特性,即玛琳斯效应。根据式3给出的方程计算产品的实际永久变形为13mm,通过对分析结果进行相应偏移得出实际产品的载荷位移曲线,如图9所示。对比分析结果和实测结果不难看出,分析结果的曲线落在测试曲线的损伤区域以内,具有较高的符合性。
分析与测试结果在屈曲区仍旧存在误差,主要原因是:(1)在试样的压缩实验时其摩擦系数无法保持压缩过程中与初始状态保持一致;(2)产品在发泡工艺上存在于温度压力等相关性;(3)模型简化方式、约束条件、摩擦系数均会对分析结果造成影响。
5 结语
首先,在进行聚氨酯缓冲块的有限元分析中,通过简单压缩实验和单轴拉伸实验来获取材料的本构参数的方式是可行的。为能适应更多产品的分析,应变应该涵盖大部分产品可能的范围。
其次,通过不同应变等级获取到的R.W.Ogden和D.G.Roxburth本构参数可以模拟材料初始状态和软化后的静态性能。
再次,由于不同的应变等级下产生的永久损伤不相同,通过试样的压缩实验能反应产品的永久变形情况,结合一系列的应变等级和永久应变建立等效方程,证实了这方案的可行性。
最后,实验和分析对比表明,两者存在较高的吻合度,对工程设计具有较好的指导价值,同时也证明了此方法的合理性[5]。
