基于深度学习的复杂系统仿人思维控制研究
2020-08-26王培进杜晓林
王培进,杜晓林
( 烟台大学计算机与控制工程学院,山东 烟台 264005)
单输入-单输出系统(SISO)只有一个被控量、一个控制量,根据干扰量的情况,可以构成反馈、前馈-反馈、串级、前馈-反馈-串级等控制结构,控制相对简单,而复杂系统的控制就相对复杂.复杂系统一般有如下特点:
(1)有多个被控量、干扰量和控制量,是多输入-多输出(MIMO)系统;
(2)被控量与干扰量之间、控制量与被控量之间、被控量与被控量之间存在关联关系.一个控制量的输出,不仅仅影响与其特定对应的被控量的变化,同时可能影响其他被控量的变化;一个干扰量的变化,影响多个被控量的变化;同理,一个被控量的变化可能影响其他被控量的变化;
(3)各个量的变化存在时滞,有些复杂系统还是时变系统、非线性系统;
(4)由于系统的复杂性,难以建立数学模型.
以孵化机控制为例,孵化机是用于孵化鸡、鸭等用的设备,孵化过程被控量有温度、湿度、二氧化碳含量等,控制量有通风、加湿、加热等,干扰因素也很多,包括环境温度、蛋的种类等,各个量之间相互耦合,是一个典型的复杂MIMO控制系统.孵化机孵化过程要控制的指标是孵化成功率,在控制过程中,温度、湿度、通风之间存在耦合关系.温度变化滞后特性明显,湿度变化滞后小,正常情况下,温度和湿度成反比例关系,通风可以控制二氧化碳含量,同时既影响温度变化也影响湿度变化.同样,控制温度,也影响湿度;控制湿度,也影响温度.孵化机控制问题可以看作是一个三输入-三输出控制问题,难以建立准确的数学模型.孵化机常用的PID控制、解耦控制、模糊控制、模糊PID控制等控制方法,不能有效地施加控制,稳定性差.
1 复杂系统控制方法
复杂系统可以看作是多个SISO子系统构成,如果子系统之间没有耦合,可以采用SISO系统控制方法;如果有耦合,一般采用解耦控制或者其他智能控制方法.
在解耦控制问题中,基本目标是设计一个控制装置,使构成的多变量控制系统的每个输出变量仅由一个输入变量完全控制,且不同的输出由不同的输入控制.在实现解耦以后,一个多输入多输出控制系统就解除了输入、输出变量间的交叉耦合,从而实现自治控制,即互不影响的控制.
解耦控制必须有较为准确的数学模型,而一些复杂过程控制、流程控制等控制系统,数学模型难以建立,难以实现解耦控制.即使实现了解耦控制,系统的参数变化,也会破坏解耦控制的稳定性.
其他智能控制方法,例如常用的模糊控制,基于先验控制规则.对于一个没有控制经验的复杂系统,无法采用模糊控制方法.即使实现了模糊控制,也无法在线学习、修订控制规则或者控制经验.
因此,必须寻找新的控制理论和方法.
2 仿人思维控制理论简介
仿人思维控制理论揭示人的控制思维机理和控制智慧[1],克服当前控制理论在设计控制器时存在的不足,并用计算机模拟、实现,解决难以建模的系统控制问题.仿人思维控制理论研究取得的主要研究成果如下:
(1)提出从数据空间到概念空间的转换方法,定义了被控量、控制量、干扰量、稳定性、控制过程等相关概念[2-4];
(2)提出3种控制算法,模拟抽象逻辑推理控制思维[5];
(3)提出模拟形象直觉推理控制思维算法[6];
(4)提出SISO系统和MIMO系统仿人思维控制经验挖掘、调用算法[7];
(5)提出SISO系统仿人思维控制器结构,在实际控制系统中得到验证[8];
(6)提出应用于复杂系统控制的仿人思维复合控制策略[9];
(7)提出拟人化分布式智能控制系统结构[10].
对于复杂系统的控制,仿人思维控制理论给出了仿人思维复合控制策略,解决了孵化机孵化过程控制问题,但在控制经验挖掘方面仍然不完善.本文将深度学习和仿人思维控制机理相结合,解决复杂系统仿人思维控制经验挖掘问题.
3 深度学习简介
AlphaGo击败围棋国际顶尖选手使深度学习成为当今人工智能领域最热门的话题.尤其是AlphaGo Zero,在训练中不依赖于人类的棋谱,不使用人工设计的特征作为输入,将策略网络和价值网络合二为一,网络结构采用残差网络,网络深度更深,迅速自学围棋,战胜前辈AlphaGo.
深度学习是深度神经网络的简称,是一种深层次的神经网络.目前较为公认的深度学习的基本模型包括基于受限玻尔兹曼机 (Restricted Boltzmannmachine, RBM) 的深度信念网络 (Deep belief net-work, DBN)、基于自动编码器 (Autoencoder, AE) 的堆叠自动编码器 (Stacked autoencoders,SAE)、卷积神经网络 (Convolutional neural net-works, CNN)、递归神经网络 (Recurrent neuralnetworks, RNN).深度学习目前主要应用在图像处理、语音处理、自然语言处理等方面,在控制领域的应用研究刚刚起步.深度学习在控制领域主要有4个方面的研究:控制目标识别、状态特征提取、系统参数辨识、控制策略计算等.
综观文献[11-19]:(1) 深度学习在控制领域的研究已经开始,但研究成果不多,尤其在控制策略应用研究方面更少,且局限于单输入-单输出系统(SISO),对多输入-多输出(MIMO)复杂系统控制策略的应用研究,未见相关论文报道;(2)AlphaGo、AlphaGo Zero的出现,对深度学习在控制领域的研究带来新的动力和想象力.
4 深度学习与仿人思维控制
人脑是世界上最优秀的控制器,一个有经验的控制专家,可以同时观测多个量的变化(多传感器输入),利用手、脚可以实现多个控制动作(多控制量输出),以达到给定的控制目的.经过长时间的控制,积累了丰富的控制经验,他知道哪个被控量变化了,应该执行一个或几个控制量,可以抑制其变化;同时由于被控量之间的关联关系,还要调节另一个或几个被控量,以抑制因前面施加控制动作带来的变化.人工控制能够实现开、闭环切换,能够做到有针对性的控制而不是连续控制;能够根据干扰量的变化特点和被控制量的变化特点而施加控制,这种控制带有选择性.传统控制方法是只要干扰量和被控制量有变化,或者系统参数有变化,就有控制动作产生,导致系统波动,控制方法如果鲁棒性不好,严重的可能出现不稳定.
AlphaGo Zero 能够通过自学习积累丰富的下棋经验,这跟人工控制过程十分相似.AlphaGo Zero之所以成功,在于围棋有给定的下棋规则和输赢判定标准.同样,人工控制过程也有给定的控制规则和控制有效性判定标准.因而,利用AlphaGo Zero的深度学习机理,模拟人的控制思维是完全可行的.人工控制过程的控制规则是消除干扰、抑制干扰,保持被控量的稳定.每一次控制是否有效,可以用以下标准来判断,符合其中之一,该次控制有效,可以记忆保存.
(1) 偏差是否减小
|en+1| < |en|;
(2) 被控量变化趋势是否改变
从Δen>0 到 Δen+1<0,或者从 Δen<0 到 Δen+1>0;
(3) 被控量是否进入稳定区域,相对稳定
|Δen|=|yn+1-yn|=|Δyn|≈0;
(4)控制最终是否有效,可以用以下标准判断:
|en|≤ε,|Δei|≈0,oren=0.
其中,ε控制精度,e被控量偏差,y被控量当前值.
满足上述条件之一,可以从闭环控制变为开环控制,保持控制量输出不变.
当然,人工控制过程与AlphaGo Zero下棋最大的区别在于:AlphaGo Zero 下棋动作无论出现多大的失误,都可以自身校正,不影响最终结果,不存在安全、稳定等问题.但是,人工控制过程每一次控制动作的产生,都是小心翼翼的,以防止引起被控量的巨大波动,导致系统出现严重不稳定和某些危险.可见,如果将类似于AlphaGo Zero的深度学习网络用于实际系统的实时控制,不能从零开始学习,必须先基于一定的控制经验学习,然后再边控制边学习,积累新的控制经验,用于实时控制.如果从零开始学习,有可能产生一些非理性的输出,产生危险控制动作,导致被控系统出现严重问题.因此,必须结合AlphaGo、AlphaGo Zero设计深度学习控制网络,模拟人的控制思维,解决复杂系统的控制,这是将深度学习网络用于实际控制系统的重要特征.
5 仿人思维深度学习控制网络
控制的根本目的是消除干扰、抑制干扰,达到给定的控制目标.假定被控量为xi(i=1, 2, …,n),有n个;干扰量为dj(j=1, 2, …,m),有m个;控制量ur(r=1, 2, …,k),有k个,这些量之间存在关联关系或者耦合关系.控制的任务是:根据当前被控量变化、干扰量变化和控制量当前值,确定下一步控制量的输出,使被控量达到符合给定控制要求.若达到给定控制要求,由闭环控制转换为开环控制,“等一等,看一看”,根据被控量变化情况,决定是否要施加控制作用,同时将当前的输入-输出作为一条控制经验进行存储.若没有达到给定控制要求,则继续施加控制作用.
深度学习神经网络的实质是以多层的带有一定特征的网络,以更高的精度逼近输入-输出之间的复杂的非线性关系.对于MIMO复杂系统,输出控制量和输入被控量、干扰量之间存在复杂的非线性关系,可以用深度学习神经网络来模拟它们之间的关系.
5.1 网络架构
根据我们的研究[1],人脑的语言不是数学的语言,人脑主要是基于概念的推理与思考,使用if-then的推理规则.在实际控制系统中,多个传感器输出被控量、干扰量的实时数据,加上控制量的当前值,形成数据空间.模拟人的控制思维,必须将输入数据空间转换为概念空间,通过各个概念之间的关系,形成推理规则,然后再将概念空间转换为数据空间输出控制量.为此,我们定义了如下几个空间,便于模拟人的控制思维.
输入数据空间:传感器阵列获得的被控量、干扰量(可测的)实时值,控制量当前值.
输入特征量空间:被控量的偏差、偏差的变化,干扰量的变化量.
输入概念空间:被控量变化的大小、方向、速度、趋势,干扰量变化的大小.
规则空间:被控量、干扰量、控制量之间构成的关联规则.
输出概念空间:控制量大幅增加,小幅增加、大幅减小、小幅减少、保持不变、最大、最小.
输出数据空间:各个控制量输出实时值.
输入、输出概念空间的定义及其对应特征量值,见前期研究见文献[2-3].
对于控制规则空间的定义,需要挖掘语言值关联规则.语言值关联规则为“如果X是A,则Y是B”,判断一个语言值关联规则是否被采用需要用到支持度和信任度.当支持度和信任度分别不小于给定的最小支持度和最小信任度时,则认为语言值关联规则被采用,否则不被采用.人工控制过程中丰富的控制知识的形成过程可以看作是人认知过程中从数据到概念,从概念到规则的发现过程.
对于MIMO系统,假定只有2个被控量x1,x2,2个干扰量d1,d2,2个控制量u1,u2,它们之间存在关联与耦合关系.一般控制经验表达规则可以是:
ifx1andx2andd1andd2thenu1andu2;
ifx1andx2andd1ord2thenu1andu2;
ifx1andx2ord1ord2thenu1andu2;
ifx1andx2ord1andd2thenu1andu2;
ifx1orx2ord1ord2thenu1andu2;
ifx1orx2ord1andd2thenu1andu2;
ifx1orx2andd1andd2thenu1andu2;
ifx1orx2andd1ord2thenu1andu2.
推广到基于概念的控制经验表达,每个被控量有4个特征量:变化的大小、方向、速度、趋势;每个特征量有不同的特征值,对应的特征值分别有7个、3个、3个、3个;干扰量有1个特征量,有7个特征值;控制量输出有7个特征值.用被控量、干扰量、控制量特征值表达控制规则,全部转换为逻辑与形式,例如:
ifx11=3 andx12=1 andx13=1 andx14=0 andx21=3 andx22=1 andx23=1 andx24=0 andd11=0 andd21=0 thenu1=u1maxandu2=u2max.
其中,xij表示被控量xi的第j个特征量,j=1,2,3,4;di1表示干扰量di的特征量.这些形式的组合数上万种.从组合数从上万种中抽取常用的、有效的控制规则组合,对于一个给定的控制系统,大约为几十种,这个过程可以看作是逐步抽取特征的过程,这跟图像识别类似,从几万像素中,经过特征识别,抽取需要识别的特征字符.由此推论,基于卷积神经网络的深度学习网络可以用于模拟人的控制思维与控制经验.卷积神经网络适合于特征提取,基于卷积神经网络的深度学习网络可以实现多级特征提取,根据上述分析,在实时控制过程中,用基于卷积神经网络的深度学习网络挖掘人的控制经验.仿人思维深度学习控制网络结构图1所示,由3个网络组成:输入网络、深度学习网络、输出网络.

图1 仿人思维深度学习控制网络组成
图2—4分别给出了每个网络的具体组成部分.
对于输入网络,是一个非全链接前向神经网络,各个层特点:
(1)数据输入层:被控量当前值、干扰量当前值.节点数是被控量和干扰量数目的和.输入层与特征层之间连接权值为1.
(2)输入特征层:被控量节点输出对应的点是偏差及其偏差的变化,干扰量输出对应的节点是干扰量的变化,特征层与概念层之间连接权值为1.
被控量输出对应的第一个节点是偏差节点,输出:y=ei.
被控量输出对应的第二个节点是偏差变化节点,输出:y=ei-ei-1.
干扰量输出对应的节点是干扰量的变化,输出:y=di.
输出激活函数为线性函数.
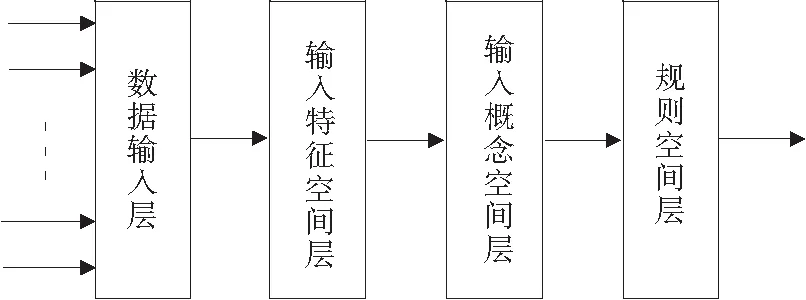
图2 输入网络组成
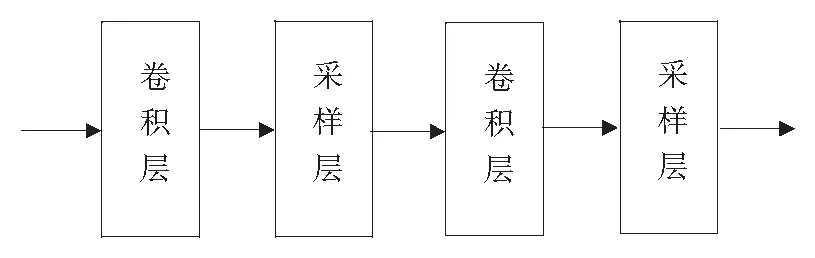
图3 基于卷积神经网络的深度学习网络
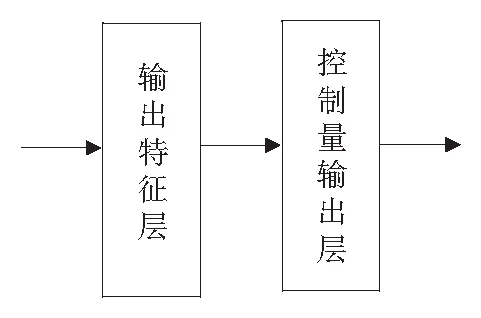
图4 输出网络组成
(3)输入概念层:与被控量输入对应的是被控量变化的大小、方向、速度、趋势4个节点,与干扰量输入对应的是干扰量变化的大小1个节点.对应被控量变化大小的节点只与偏差输出有关.
被控量变化的大小输出采用ReLU 函数,其他输出采用tanh 函数.
(4)规则空间层:按照前述的控制规则,规则层节点数很多,它与概念层之间是非全连接关系.只要被控量、干扰量之间有关联关系,就至少产生一个节点.对于2个被控量、2个干扰量、2个控制量的控制系统(本文实验研究系统),经过分析,选取可能出现的150种组合,构成150个节点.节点输出激活函数采用sigmoid函数,其大小反映了该节点对应的控制规则使用强度.
深度学习网络采用的是卷积神经网络:
第一个卷积层:概念层的输出经过一次卷积运算,去掉一些不常用的控制规则.对于我们研究的实验系统,从规则层的150个节点压缩到120个节点.
第一个采样层:采样层也称池化层,去掉使用强度不高的控制规则,将节点数压缩到100个.
第二个卷积层:再经过一次卷积运算,去掉一些不常用的控制规则,将100个节点压缩到80个节点.
第二个采样层:进一步去掉使用强度不高的控制规则,将节点数压缩到50个.也就是常用的、有效的控制规则为50个.
输出网络是一个2层的前向神经网络:
输出特征层:输出特征层有6个节点,对应6种输出,它与前面的采样层是非全连接方式.每个控制规则对应一个给定的输出特征值,因而对应给定的节点,而不是所有的节点.特征层输出激活函数采用sigmoid函数.
控制量输出层:输出层节点数就是控制量的个数,对应本实验研究系统是2个.输出层与输出特征层之间是全连接关系,也就是说,任何一个控制量的输出是6种特征输出的组合.输出层激活函数采用ReLU 函数.
5.2 网络的训练与学习
如前所述,由于控制的特殊性,仿人思维深度学习控制网络不能像AlphaGo Zero 那样从零开始自我学习,必须有一定的控制经验,然后再边控制边学习边强化,以应对各种控制情况,我们提出2种解决方法.
5.2.1 先验式训练与学习法 对于给定的控制系统,如果有条件可以进行手动控制,先进行手动控制(利用组态界面,手动改变控制量输出大小),取得训练数据,对控制网络进行训练.将训练好的控制网络进行实时在线应用,在控制过程中进一步训练网络,取得更丰富的控制经验.
也可以通过理论分析或类似系统的控制经验,分析出一定数量的控制经验,对控制网络进行训练,将训练好的控制网络进行实时在线应用.
5.2.2 尝试式训练与学习法 将复杂系统按照被控量、干扰量、控制量之间的强关联关系,划分几个相对独立的子系统,每个子系统设计基于仿人思维控制的智能反馈、智能前馈-反馈、智能串级、智能前馈-反馈-串级等控制结构,主回路控制器采用我们研究的仿人思维控制算法——三阶段控制法[1],副回路控制器采用我们研究的智能前馈控制器[9]等.设计好各个子系统,开始控制.这个阶段是试探性控制阶段.该阶段的控制,可以实现“快速”控制,接近给定控制要求,但不能保证“稳、准”的控制要求.在控制过程中,保存控制有效的数据,对控制网络进行训练.网络训练完毕后,训练控制子系统不再发挥作用,系统控制由控制网络接管.
5.2.3 训练学习约束条件 经过初级阶段训练好的网络,在实时在线控制过程中,利用有效的数据进行在线训练,获取更丰富的控制经验.由于控制的特殊性,实时训练过程需要考虑如下约束条件.
(1)控制量输出大小约束:对于一组给定的输入数据,经过控制网络计算输出的控制量值必须在最大与最小之间,若超出,自动选择上限值或下限值.
(2)控制量输出变化约束:在被控量变化不大的情况下,控制量输出变化不能过大,即
|Uk-Uk-1|≤∮.
如果计算的控制量超出上述约束条件,不能直接施加控制,需要做适当修正:
U输出=U计算-Kp·Δu.
(3)控制有效性约束:对于一组给定的输入数据,经过控制网络计算的控制量,施加到被控系统后,如果满足如下条件之一,说明控制是有效的,该组数据可以保存,与前面初始训练数据一起用于控制网络的实时训练.
(a) 偏差是否减小: |en+1| < |en|;
(b) 被控量变化趋势是否改变:从 Δen>0 到 Δen+1<0,或者从 Δen<0 到 Δen+1>0;
(c) 被控量是否进入稳定区域,相对稳定:
|Δen|=|yn+1-yn|=|Δyn| ≈0.
(4)训练学习终止约束:当如下条件满足时,控制网络的在线训练学习可以终止.
每个被控量达到给定的控制精度:|en|≤ε,可以从闭环控制变为开环控制,保持控制量输出不变.
6 实验研究
实验系统采用三水箱液位控制系统,图5是实际对象示意图,图6是其结构工艺原理.

图5 实验系统
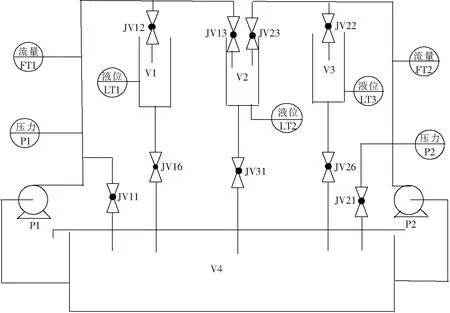
图6 实验设备工艺原理
如图5、6所示,V1,V2,V3为小水箱,V4为储水箱.V1,V3水箱的液位可以单独控制,V2水箱液位可以由P1,P2 2个直流伺服电机输出的水流控制.JV11,JV21 2个手动阀可以调节供水流量,用于控制中施加干扰量.我们实验设置是控制V1、V2水箱的液位,且V2液位大于V1液位,因而控制系统的被控量是2个水箱的液位,干扰量是两路流量,控制量是2个直流伺服电机施加的电压,即系统2个被控量,2个干扰量,2个控制量.它们之间的耦合关系是:V2水箱液位受2个控制量控制,一个控制量改变,另一个控制量也必须改变,才能保证液位不变.V1水箱液位可以单独控制,但是对它施加的控制必然影响V2水箱液位.控制逻辑关系如下:
初始控制阶段.先对V1水箱液位施加控制,使其达到给定控制值,然后通过调节P2电机转速,调节右路流量,使V2水箱液位达到给定控制值.
抗干扰控制阶段.例如,加大JV16手动阀的开度,V1水箱液位下降,通过控制加大P1电机转速,增大左路流量,使V1水箱液位恢复到给定控制值,同时减小左路流量,保证V2水箱液位不变.反之,亦然.控制经验为
If V1水箱液位减小 and V2水箱液位不变 then P1电机转速增大and P2电机转速减小.
同理,通过分析可以推理出如下几条控制经验:
If V1水箱液位增大 and V2水箱液位不变 then P1电机转速减小and P2电机转速增大;
If 左路流量减小 and V1液位不变and V2液位不变 then P1电机转速增大or P2电机转速增大or P2电机转速不变;
If 左路流量增大 and V1液位不变and V2液位不变 then P1电机转速减小or P2电机转速减小or P2电机转速不变;
If V1液位不变and V2液位减小 then P1电机转速不变and P2电机转速增大;
If V1液位不变and V2液位增大 then P1电机转速不变and P2电机转速减小;
If V1液位减小and V2液位减小 then P1电机转速增大or P2电机转速增大or P2电机转速不变;
If V1液位增大and V2液位增大 then P1电机转速减小or P2电机转速减小or P2电机转速不变;
If V1液位增大and V2液位减小 then P1电机转速减小and P2电机转速增大;
If V1液位减小and V2液位增大 then P1电机转速增大and P2电机转速减小;
If 右路流量减小 and V1液位不变and V2液位不变 then P1电机转速不变and P2电机转速增大;
If 右路流量增大 and V1液位不变and V2液位不变 then P1电机转速不变and P2电机转速减小.
利用上述控制经验,手动控制每条控制经验获取5组数据,共获取60组实验数据,对深度学习控制网络进行训练.训练完毕,参与实时闭环反馈控制.控制系统结构如图7所示.
实际实验过程中,采用组态王做监控软件,但它不能实现复杂的算法.控制网络的在线实时训练,其训练算法是很复杂的,涉及矩阵运算、优化、迭代、函数计算等.因此,让组态王完成在线训练与应用,实时性难以做到,编程困难.为解决这一问题,我们采用了DDE技术,实现MatLab、组态王之间的数据交换,发挥各自的特长.MatLab实现神经网络的训练与计算十分简单;组态王可以通过DDE技术与其他软件通讯,编制监控界面方便.
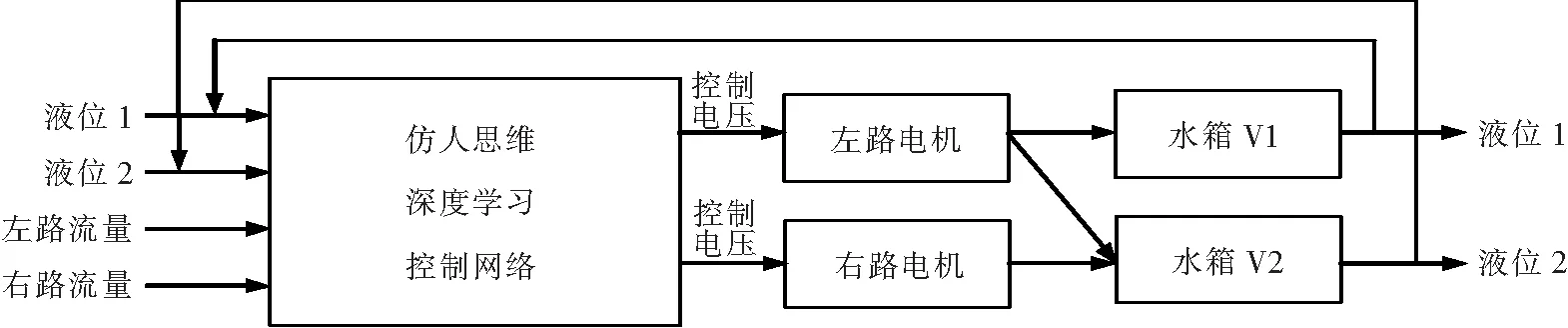
图7 实验控制系统
图8、图9给出了训练好的控制网络进行的闭环控制实验曲线.如图所示,液位1随着左路流量的增大、减小发生变化很大,或者上升,或者下降.在控制过程中,尽管左路流量波动较大,液位1波动很大,但是液位2基本没有变化,始终在给定值附近(控制精度为1),这是右路及时控制的结果.实验结果表明,训练好的控制网络,模拟了人的控制思维,成功地实现了解耦,取得优良实验结果.
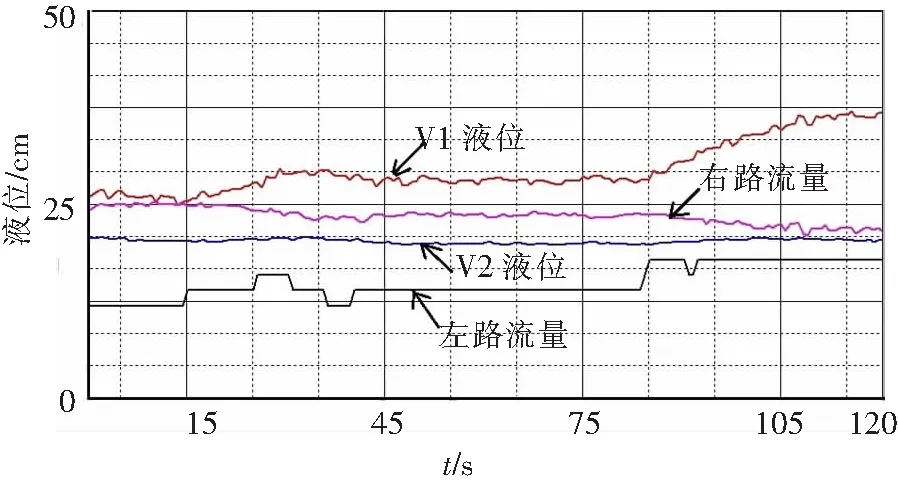
图8 实时控制曲线(1)
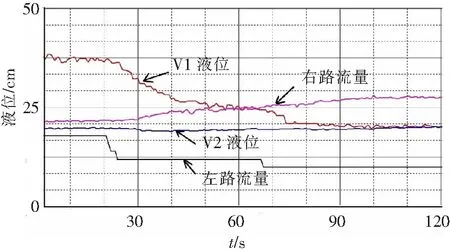
图9 实时控制曲线(2)
7 总 结
复杂系统有多个输入、输出,输入、输出变量之间一般存在耦合关系,对一些复杂的过程控制系统难以建立数学模型,控制相对复杂.现有控制理论解决复杂系统控制问题,仍然存在不足.仿人思维控制是基于人控制思维和控制智慧的控制方法,跟其他控制方法不同之处在于:(1)能实现开环、闭环切换;(2)分段控制,不同阶段采用不同控制方法;(3)依据被控量变化的大小、方向、速度、趋势确定控制策略;(4)采样周期、控制周期在控制过程是可变的;(5)控制过程实时挖掘控制经验与技巧,指导控制过程;(6)依据被控量、控制量、干扰量的动态特性以及它们之间的关系确定控制策略;(7)能够有机地融合人的思维智能、动觉智能、视觉智能;(8)能够协调“稳、快、准”3个控制性能指标之间的统一.仿人思维控制理论方法已经成功地运用于单输入-单输出过程控制系统,对多输入-多输出复杂系统控制也有应用,但也存在不足.深度学习网络可以实现类似人脑边学习、边积累经验功能,将仿人思维控制机理与深度学习网络结合,发挥各自的优势,解决复杂系统控制问题是可行的.我们研究了2个被控量、2个干扰量、2个控制量的实验控制系统,实验结果表明,我们提出的仿人思维深度学习网络取得良好的控制效果.下一步将研究更加复杂的多输入-多输出系统控制,完善基于仿人思维深度学习网络的控制方法.
